培养学生科学思维和创新能力的研究与实践
——谈大学数学研究型教学
郑连存, 张 艳
(1.北京科技大学数理学院,北京100083; 2.北京建筑工程大学理学院,北京100044)
1 引 言
美国心理学家吉尔福特提出:发散思维是创造性思维的核心,它决定了一个人创造力的高低.
高等教育承担着为国家培养具有创造思维的创新型人才的神圣使命,作为高等教育工作者,我们深深感受到培养创新型人才的重要责任.笔者认为在大学教学活动中,引导学生深入理解所学知识,培养学生独立思考和创新能力应是教学工作者的最高追求.
笔者多年来一直工作在教学第一线,担任多门本科生和研究生基础课教学工作,教学中始终注意将自己多年从事科研工作的思想和体会融入到教学活动中,注意发散思维和创新能力的培养.笔者承担《高等数学》和《工科数学分析》课程教学工作时,经常以讨论课的形式,将一些有启发,有延拓性的题目首先交给学生去讨论,探讨不同解法及给出各种正确答案.题目做完后,引导学生分析题目的本质及各种关联问题并由学生自己拓展改编题目,引导学生沿着各种不同的途径去思考,类比、联想、猜想、发现和论证.下面从一个关于导数值的等式问题出发,来探讨教师在课堂教学过程中如何根据教学内容创设能激起学生新异感的问题情景, 善于能从一个问题出发,沿着各种不同的途径去思考,使学生的思维不断攀升到更高的阶段,丰富教学内容,扩大课堂信息量,激发学生学习兴趣,发现多种关联问题及寻求解决问题的途径,培养学生的发散思维和创新能力.
2 一个关于导数值关系式的例题
人们经常把创新想象得很高深、很神秘、很复杂,并因此阻碍了自己的创新.很多创新工作,甚至是非常伟大的创新,有时它的思路也很简单,往往和某些已经知问题相关联.
例设函数f(x)在区间[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1,证明在(0,1)内存在两点x1,x2使得

(1)
先由学生自己给出不同证明方法,这里仅列出一种证明方法如下:


故
按照常规教学方式,题目证明完,学生理解掌握,教学任务就完成了.但是实际上还有很多问题有待思考.该问题的本质是什么?证明中的关键因素是什么?可以联系到或衍生出什么不同问题?
3 发散思考:联想、猜想、论证
保持原函数特征推广
联想1(加权系数变化拓展) 首先容易联想到的一个简单变形是原问题可以化为

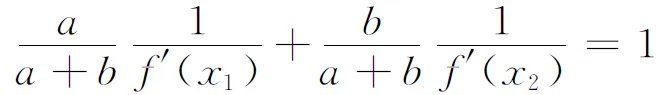
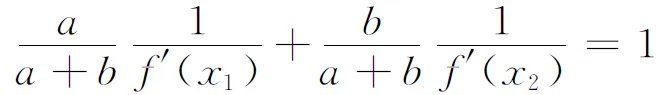
(2)

联想2(多个结点加权平均) 上面讨论涉及到(0,1)区间内两个点导数值倒数的加权平均.进一步,很自然会联想到在区间(0,1)内多个点的加权平均,若考虑到多个点的加权会有什么结果? 引导学生猜想、猜想、发现并证明如下命题.


(3)
提示 可以先考虑可以先考虑三个点情况,选取0 进一步思考和联想: (4) 联想4(函数值变化拓展) 若将例题条件f(0)=0,f(1)=1 改为f(0)=0,f(1)=a会有什么结果?引导学生猜想、猜想、发现并证明如下命题. 命题4设函数f(x)在区间[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=a(a>0),证明在(0,1)内存在两点x1,x2使得 (5) 联想5联想到两个函数值变化情况,若将例题条件f(0)=0,f(1)=1改为f(0)=a,f(1)=b,结果如何?引导学生猜想、发现并证明如下命题. 命题5设函数f(x)在区间[0,1]上连续,在(0,1)内可导,且f(0)=a,f(1)=b(b>a>0),证明在(0,1)内存在两点x1,x2使得 (6) 同样可以考虑区间[0,1]上多个点加权平均,当某些点函数值变化时的类似推广,略. 构造复合函数推广 若将例题的思想拓展到复合函数,会有什么结果?假设已知函数u=F(y),y=f(x),复合函数u=F(f(x))满足在某个闭区间上连续,在相应的开区间内可导,且F(0)=0,F(1)=1.将u=F(y)带入公式(3)或(4),可以得到关于f(x)的许多新问题. 联想6令F(x)=ln[f(x)],引导学生猜想、发现并证明如下命题. 命题6设函数f(x)为定义在区间[0,1]上连续,在(0,1)内可导的正值函数,f(0)=1,f(1)=e,k1,k2,…,kn为n个正数,证明在(0,1)内存在n个不同的点x1,x2,…,xn,使得 (7) (8) 命题6及命题7的证明令F(x)=lnf(x),则当x∈[0,1]时,函数F(x)满足区间[0,1]上可导,且F(0)=0,F(1)=1,F(x)满足原问题的条件,由公式(3)或(4),立即得到证明. 类似地,可以做很多其它形式的推广,如F(x)=ef(x),exf(x),e-xf(x), cos(f(x)),…,这里从略. (9) 更一般地,有 命题9(复合函数拓展) 在(0,1)内存在n个不同的点x1,x2,…,xn,使得 (10) 命题10(复合函数拓展) 在(0,1)内存在n个不同的点x1,x2,…,xn,使得 (11) 亦可以引入下面的复合函数拓展: 假设已知函数x=φ(t),t∈[0,1];y=f[φ(t)]是关于x=φ(t)的复合函数,φ′(t)在[0,1]上连续且不为0,当t由0连续变为1时,y由0连续变为a.y=f[φ(t)]满足区间[0,1]上可导,且f(0)=0,f(1)=a.这时可以将y=f[φ(t)]带入公式(3)或(4),立即可以得到关于f(x)的许多新问题.这里从略. 还可以将如上问题推广到二元函数或多元函数,需要用到雅克比行列式等知识.这里从略. 21世纪的竞争实质上是知识创新和技术创新的竞争,归根到底是具有创新能力的高素质人才的竞争.一个人的创新能力特别是创新思维能力的强弱将决定他未来的发展前途,一个民族的创新能力决定着其在国际竞争中的地位和作用.创新能力不是与生俱来的,而是通过学习、训练产生和提高的.高等学校是高素质人才的培养基地,高等学校教育教学改革是一项长期持久的系统工程.高等数学是大学中最重要的基础课程, 对于后续课程的学习和学生创新思维的培养, 具有重要而深远的意义.要培养学生的创新能力,教师必须在教学中引导学生掌握科学思维方法,用联系的、发展的、全面的观点看待事物和思考问题,激发学生求新求异的心理,提高学生善于发现和把握改变现状的契机和机遇,探索解决问题的多种方法,为国家输送更多具有竞争力的高素质人才. [参 考 文 献] [1] 郑连存.从曲线积分的教学谈对知识的追踪溯源—培养学生科学的思维方法[J]. 高等理科教育,2005(3): 38-40. [2] 陈兆斗,郑连存,王辉,李为东.大学生数学竞赛习题精讲[M].北京:清华大学出版社,2010:34-45. [3] 斐礼文. 数学分析中的典型问题与方法[M]. 北京:高等教育出版社,2003:186-207. [4] 郑连存,张艳,联想-猜想-论证,培养学生的发散思维和创新能力[J]. 教育学文摘,2013,325(1):148-151. [5] 徐利治,王兴华. 数学分析的方法及例题选讲(修订版)[M]. 北京:高等教育出版社,1983:116-182.








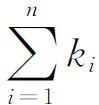








4 结束语

