钢/芳纶/钢三明治板抗高速破片侵彻性能研究*

徐 锐，戴文喜，徐豫新，马 峰，王树山

（1北京理工大学爆炸科学与技术国家重点实验室，北京 100081;2中国舰船研究设计中心，武汉 430064）

0 引言

复合材料三明治板通常由金属材料面板和复合材料芯板层合而成，其对冲击载荷的防护性能是近年来国内外研究热点领域之一。钢/芳纶/钢叠层三明治板是复合材料三明治板的一种，其通常采用高硬度金属面板和高韧性纤维增强复合材料芯板层合而成，具有高硬度、高强度、高韧性、低密度、低成本等特点，可应用于装甲车辆、舰船等武器装备的壁面，以防护杀爆战斗部爆炸产生的破片和冲击波等毁伤元的冲击破坏，相关研究受到国内外研究者的广泛关注［1～2］。徐豫新［3］针对纤维增强复合材料三明治板对破片的防护机理进行了试验研究，通过试验结果分析获得了芳纶纤维增强复合材料三明治板较玻璃纤维增强复合材料三明治板吸能特性更优的结论。对于高强度装甲钢面板和较厚夹层复合材料板的纤维增强复合材料三明治板抗破片侵彻性能研究国内尚未见报道。因大质量破片高速加载的试验费用较高，目前数值仿真是研究该类问题的一种有效手段，通过数值仿真获得的结果可为纤维增强复合材料三明治板的设计提供参考。

针对钢/芳纶/钢叠层三明治板，通过AutoDyn有限差分程序进行各种质量破片对夹层厚度不同的三明治板侵彻的数值仿真。通过数值仿真获得25 g、40 g、55 g、70 g、85 g 和 100 g 质量的破片模拟弹丸（Fragment Simulation Projectile）对前、后面钢板厚度分别为5 mm和10mm、夹层芳纶纤维（Kevlar-129）增强复合材料板厚度分别为30 mm、40 mm、50 mm、60 mm、70 mm和80 mm夹层厚度的三明治板的弹道极限;并据此进一步分析了夹层厚度对破片弹道极限和三明治板比吸收能的影响规律。

1 数值仿真

1.1 数值仿真的控制方程

AutoDyn程序是以质量守恒、动量守恒、能量守恒为根本进行计算的，数值仿真所遵循的控制方程如下:

1）质量守恒

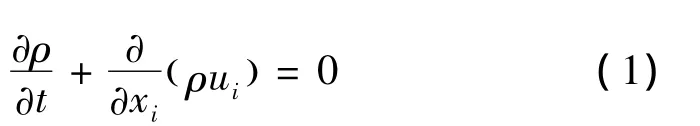
2）动量守恒

3）能量守恒

式中:ρ为材料密度;ui为速度;fi为单位质量的外力;σij为应力张量;e为总和比能，等于比动能和比内能E之和。

1.2 仿真模型

1.2.1 几何模型及离散化

1）破片

战斗部壳体在爆炸载荷驱动下产生的自然破片为不规则形且形态具有随机性，这给装甲防护结构设计及其抗弹性能的评估带来很大的不确定性。为了建立具有通用性的破片侵彻试验方法，国外通常使用破片模拟弹（Fragment Simulating Projectile）进行弹道冲击研究［4］。根据半穿甲 /整体爆破战斗部壳体破碎性数值仿真分析，确定数值仿真中采用的破片模拟弹结构尺寸如图1，尺寸列于表1。

表1 各种质量破片尺寸

图1 破片结构

根据破片和靶体结构尺寸，选用“cm·μs·g·Mbar”单位制和1/2面对称方法建立数值仿真所需的模型，破片采用0.5 mm的网格尺寸，通过TrueGrid建立数值模拟所需的几何模型并离散化后导入AutoDyn程序中，如图2所示。

图2 破片网格结构

2）靶体

设置靶体的长 ×宽为120 mm×120 mm，远大于破片破坏区域直径，结构各层厚度视具体工况确定，靶体四周施加固定约束，靶体破坏区域采用1.0 mm的网格尺寸，同样通过TrueGrid建立数值模拟所需的几何模型并离散化后导入AutoDyn程序中，如图3所示。

图3 靶板结构及离散化

1.2.2 材料模型及参数

1）纤维复合板材料模型及参数

复合材料本构行为的合理描述是近年来材料学、力学领域的研究热点之一，现阶段通常采用两种方法进行处理:一是将复合材料作为均质各向异性材料处理;二是从细观的角度考虑复合材料的非均匀性。目前，第一种方法已取得了一些满意的结果;第二种方法虽也十分重要和必要，但难以应用于宏观断裂的定量分析。参考已有研究成果采用Puff状态模型和Von Mises强度模型进行数值模拟。根据文献［5］中材料力学性能的实测值获得Kevlar-129纤维材料的模型参数，列于表2中。

表2 数值模拟用纤维增强复合板材料模型及参数

2）装甲钢材料模型及参数

采用Johnson-Cook模型描述前后装甲钢材料的本构关系，对于其状态变化用Mie-Grüneisen描述，参数列于表3。

表3 装甲钢材料参数

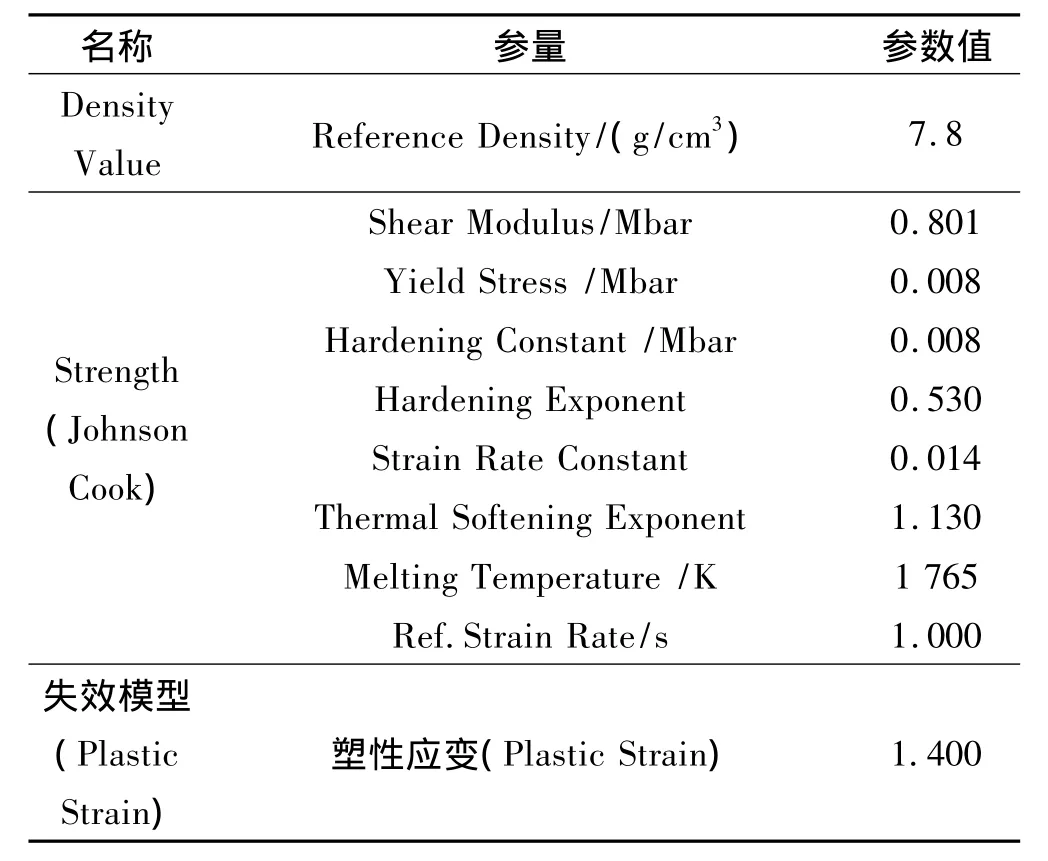
续表

3）破片材料模型及参数

对于破片用35CrMnSi材料，选用线性（Linear）模型描述材料的状态变化，选用Von Mises模型描述材料的强度，选用塑性应变（Plastic Strain）描述材料的失效（Failure）与侵蚀（Erosion），根据王琳［6］的研究结果获得模型参数设置，模型参数设置列于表4中。

表4 数值模拟用35CrMnSi钢的材料模型及参数

2 数值仿真结果分析

2.1 破片的弹道极限

针对25 g、40 g、55 g、70 g、85 g 和100 g 等6 种不同质量破片模拟弹丸对前、后面钢板厚度分别为5 mm和10 mm、夹层芳纶纤维（Kevlar-129）增强复合材料板厚度分别为30mm、40mm、50mm、60mm、70mm和80 mm等6种不同结构尺寸钢/芳纶/钢层合三明治板侵彻的的数值仿真，获得典型穿甲过程示于图4中。采用两射弹弹道极限法，获得不同质量破片贯穿不同结构三明治板的弹道极限（注:由于实际情况下破片着靶速度很难大于 2 500 m/s，速度大于2 500 m/s的情况未进行计算），列于表5中。根据表5中的数据获得不同质量破片的中间夹层Kevlar材料厚度－弹道极限速度曲线，如图5所示。

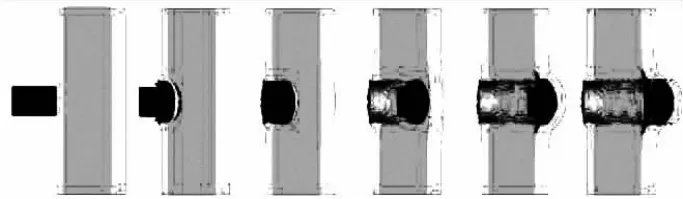
图4 破片穿甲过程

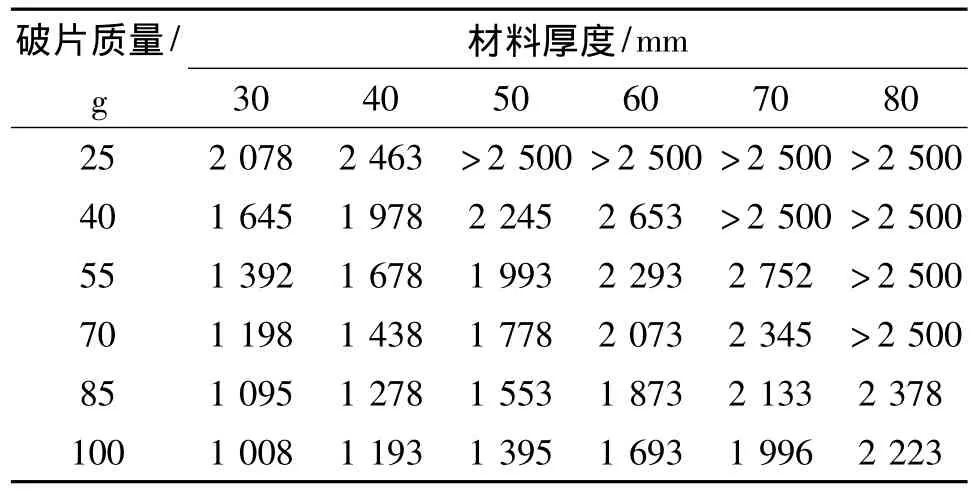
表5 6种质量破片对中间夹层Kevlar厚度不同靶板的弹道极限速度（m/s）

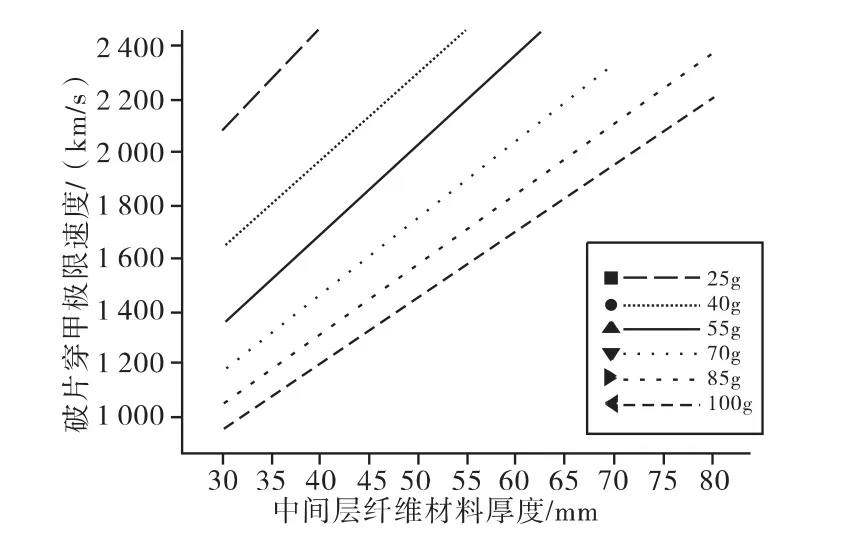
图5 不同质量破片的中间夹层Kevlar材料厚度－弹道极限速度曲线

根据徐豫新［3］的研究可知:

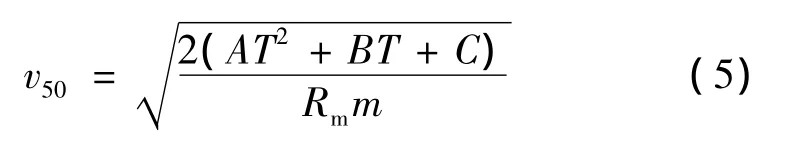
式中:v50为破片对纤维增强复合材料三明治板的弹道极限速度;t为夹层板厚度;Rm为夹层板的吸能比率;m为破片质量。其中，在前、后板厚度相同的情况下，同种材料不同厚度夹层板的吸能比率Rm基本恒定。由式（5）和图6可得，破片穿甲极限速度v50与中间层厚度T呈线性关系，拟合关系式为:

各种质量破片穿甲时a、b的取值和曲线的相关系数R2列于表6中。

表6 式（6）中系数取值和曲线的相关系数R2

从表6中可以看出，随着破片质量的增加，系数a都呈增大趋势。说明破片质量越大，增加中间夹层厚度给v50带来的增益（即靶板防护性能的增益）越明显。

2.2 靶体的面吸收能

在此引入建立在弹道极限基础上的面吸收能（单位面密度的靶体吸收能）ξ来表征靶体的抗侵彻能力，其计算公式如下:

式中:m为破片质量;v为破片贯穿靶体的弹道极限。SAD为靶体的面密度。6种结构靶板面吸收能如表7所示。由表5中数据可以看出，同一厚度夹层板的靶体面吸收能基本恒定，通过线性回归获得6种不同夹层厚度复合材料三明治板的面吸收能平均值。

表7 中间夹层Kevlar厚度不同靶板的面吸收能 /（J·m2/kg）

利用表5中不同厚度靶板面吸收能的平均值经二项式拟合得曲线如图6所示。从图中可以看出，中间层厚度越大，靶板的面吸收能越高。由面吸收能的定义式以及面密度含义可知得:

式中:m0为靶板质量;s为靶板面积（6种靶板工况的靶面积相同）。由上式可以看出，面吸收能ξ是一个与靶板厚度无关的量。当m0一定时，靶板结构的面吸收能越大，v50就越大，即同等质量条件下靶板抗破片侵彻与贯穿的能力越强，防护性能越佳。中间层厚度为80 mm靶板的面吸收能是中间层厚度为30 mm靶板的3.29倍。由此表明中间夹层的Kevlar材料给靶板防护效率带来的增益明显。

图6 中间层厚度不同的靶板间面吸收能平均值－纤维材料厚度曲线

3 结论

通过材料模型和参数的合理选择，采用有限差分程序AutoDyn可实现破片对纤维增强复合材料三明治板穿甲的数值仿真，数值仿真结果具有可信度，通过对数值仿真的结果分析得到:

1）通过弹道极限曲线以及理论分析可见:弹道极限随夹层纤维的增加呈线性递增。从拟合曲线可以看出，破片质量越大，增加中间层厚度对复合材料防护性能的提升越有意义。当Kevlar厚度为80mm时，质量在70 g以下的破片无法穿透复合结构靶板。

2）通过引入面吸收能的概念，来表征和研究靶体的抗侵彻能力，得出结论如下:中间层kevlar材料厚度越大，靶板的面吸收能越高，两者增加呈二次函数递增关系，中间层厚度为80 mm靶板的面吸收能是中间层厚度为30 mm靶板的3.29倍。说明在靶面积和靶体质量相同情况下，随着中间层Kevlar材料厚度增大，复合材料板抗破片侵彻与贯穿的能力越强，即Kevlar材料厚度的增加给靶板防护效率带来的增益明显。

［1］赵桂平，卢天健.多孔金属夹层板在冲击载荷作用下的动态响应［J］.力学学报，2008，40（2）:194－206.

［2］王晓强，朱锡，梅志远.纤维增强复合材料抗侵彻研究综述［J］.玻璃钢/复合材料，2008，34（5）:47 －55.

［3］徐豫新.破片毁伤效应若干问题研究［D］.北京:北京理工大学，2012:98－99.

［4］王晓强，朱锡，梅志远.陶瓷/船用钢抗破片模拟弹侵彻的实验研究［J］.哈尔滨工程大学学报，2011，32（5）:555－558.

［5］徐豫新，王树山，严文康，等.纤维增强复合材料三明治板的破片穿甲实验［J］.复合材料学报，2012，29（3）:72－77.

［6］王琳，王富耻，王鲁，等.空心弹体侵彻金属靶板的数值模拟和实验研究［J］.兵器材料科学与工程，2001，24（6）:13－17.