制导动能弹最优初始参数计算方法研究*
冯必鸣,聂万胜,李 柯
(装备学院,北京 101416)
0 引言
国外曾经提出名为“上帝之仗”的动能对地打击方案,假想动能弹头离轨再入大气层,对地面目标实施精确垂直动能打击[1]。然而,寻找一组最优的初始参数既能保证动能弹在攻角和过载限制下高速精确垂直命中目标,又能使离轨制动燃料消耗量最小是实现该方案的关键。
目前,对弹药最佳初始参数的研究主要采用两种方法:搜索法和计算法。国内学者大多根据制导弹药不同的初始参数组合方案,采用搜索法寻找最佳初始条件或者是弹药投放区域[2-6],但是采用该类方法计算时,如果没有较好的搜索方式,搜索策略近乎于穷举;而计算法是将寻优过程描述成最优控制模型[7],利用最优控制理论的相关算法计算出满足某项指标最优的控制量变化情况,主要有间接法和直接法。基于Pontryagin极大值原理的间接法是根据某项性能指标最优,推导出制导律的解析解;直接法[10-12]是将连续的最优控制问题离散并参数化,针对某项指标最优得到离散的最优控制律,而在制导控制规律已经确定的条件下,计算满足各项条件的最优初始参数研究还较少。
文中采用直接法的离散思想,根据制导律和动能弹飞行状态参数之间的代数关系,将原来带控制量的微分方程组转化成为由动能弹状态参数表示的微分方程组,并通过离散过程将该方程组转化成为由一系列状态参数表示的代数方程组,通过序列二次规划法求解非线性规划问题进而得到最优初始参数。
1 参数优化计算方法
1.1 纵平面终端倾角约束制导方程
根据图1所示位置关系和文献[13]可知,动能弹纵向平面内的运动方程可以表示为:
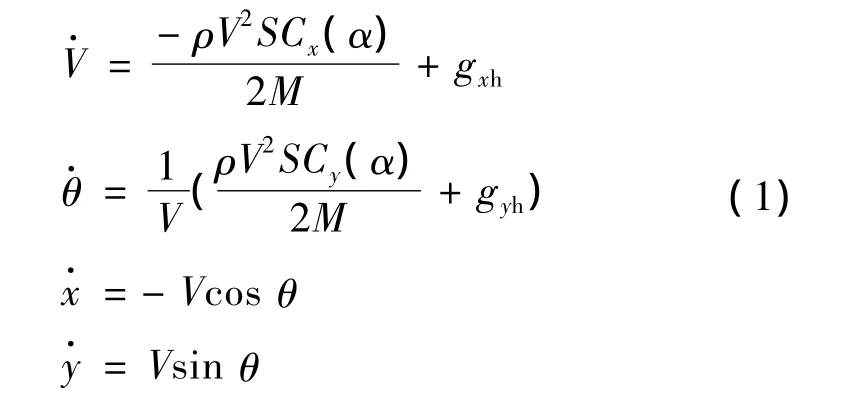
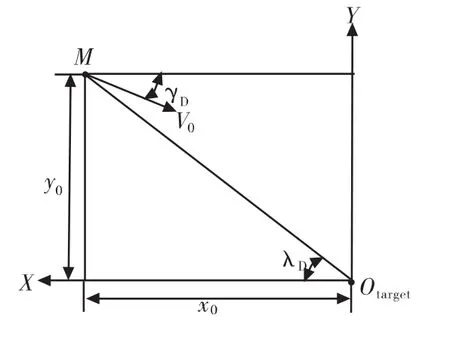
图1 弹目坐标系
在简化模型中:gxh= -ghsinθ,gyh= -ghcosθ;x为弹目距离;y为动能弹飞行高度;θ为弹道倾角(θ<0);V为弹体飞行速度。而纵向平面内的倾角约束制导律为:
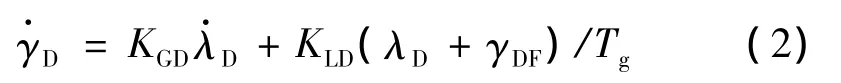
1.2 状态参数表示的制导方程
文中在进行初始参数优化时,考虑将带有控制量并满足导引律的运动方程组转化成为用状态参数表示的运动方程,并将微分方程组离散,转化成为由状态参数表示的一系列代数方程组,通过求解非线性规划问题得到最优初始参数。
根据视线坐标系和目标坐标系之间的转换关系,可得:

因此可以将纵向平面内的导引方程转变为如下形式:
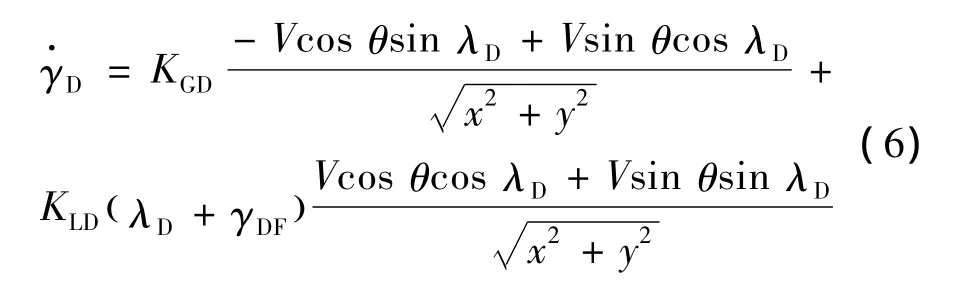

其中,ρ()y = ρ0e-()y/H,海平面大气密度 ρ0=1.226 kg/m3,参考高度 H=7254.24 m,重力加速度 gh=9.81 m/s2,动能弹气动参考面积 S=0.102 m2。
又由Cx()α=C0x+Cαxα2,可以得到:
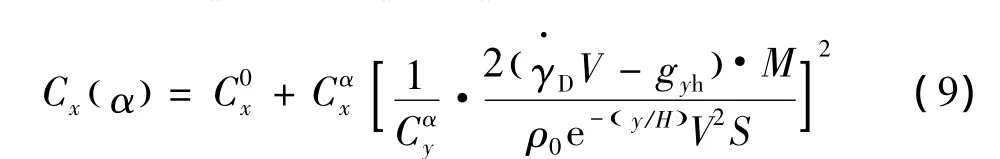
至此,可以将原来带控制量α的微分方程组变为用4个状态参数[x,y,V,θ]表示的微分方程组:

优化指标:

满足微分方程组约束.:
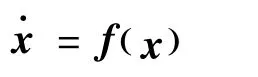
满足不等式约束:


边界条件:

1.3 微分方程组离散
现将连续的微分方程组按照Radau伪谱法的思想进行离散化处理,参考文献[15]所描述的离散过程,可以得到以下转换关系:

将上面带微分方程组约束的最优化问题转变成为用以下形式代数方程组表示的参数优化问题。
指标函数:

等式约束:
微分方程组转化的代数方程组:
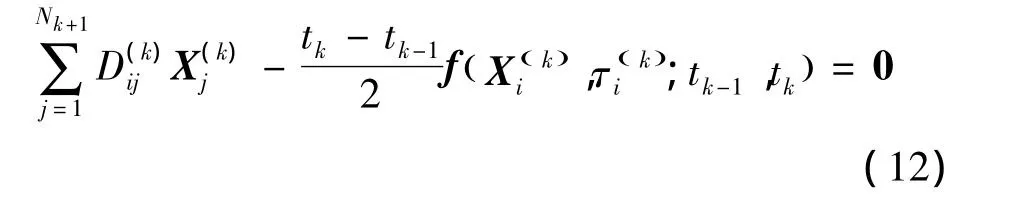
其中 i=1,……,Nk。
边界条件转化的代数方程组:

不等式约束:
攻角和过载限制转化的不等式约束:

边界条件转化的不等式约束:
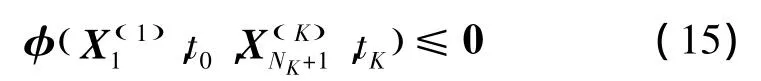

上述过程将满足制导控制律的微分方程组最优初始参数问题转化为由非线性代数方程组表示的参数优化问题,利用序列二次规划法(SQP)可求解出最优初始参数。
2 仿真研究
2.1 最小再入角研究
根据国外提出的“上帝之仗”动能打击假想,过大的再入角会造成离轨制动时较大的燃料损耗,因而通过研究满足终端命中条件的最小再入角,为开展方案可行性论证提供理论支持。文中以某型制导动能弹气动性能为例[14],研究不同速度下的最小再入角问题,该优化问题可以描述为:

在初始倾角和目标距离不确定的情况下,针对100 kg 载 荷以 8 000 m/s、7 000 m/s、6 000 m/s、5 000 m/s、4 000 m/s 5种不同速度再入,研究不同再入速度下满足终端打击条件的最小再入角,计算结果如表1所示。
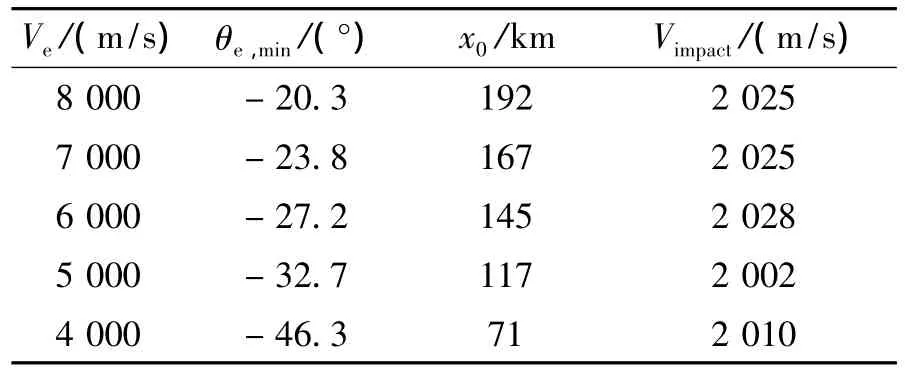
表1 不同速度对应的最小再入角对比
从表1所示结果可知,再入速度越高,最小再入角越小,目标距离更远,但是在最小再入角情况下,命中速度均不高,略大于2 000 m/s。为了说明该方法的可行性,文中选择中等再入速度5 000 m/s,采用蒙特卡洛打靶法寻找满足命中条件的最小再入角,计算结果如图2和图3所示。
从图2不难发现,速度5 000 m/s的最小再入角约为 -32.6°,与文中所用方法计算得到的最小再入角差别仅有0.1°,而目标距离之间的差别也小于500m。并且从图3所示命中速度分布情况可知,打靶法得到的最小再入角和相应目标距离对应的命中速度也接近2 000 m/s。
以再入速度5000 m/s,再入角 -32.7°,目标距离117 km为例,按照式(1)和式(2)描述的制导方程计算得到动能弹参数变化情况如图4~图6所示。从图中所示的飞行弹道、相对距离、飞行速度、弹道倾角以及攻角和过载变化情况不难发现,各项参数均满足约束要求。通过上述研究结果可以证明,文中设计的参数优化方法是可行的。

图2 再入角与目标距对应关系
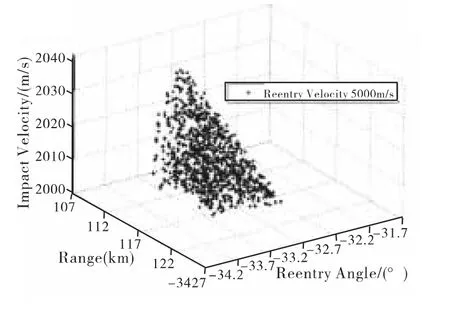
图3 命中速度分布

图4 飞行轨迹及相对距离

图5 速度及倾角
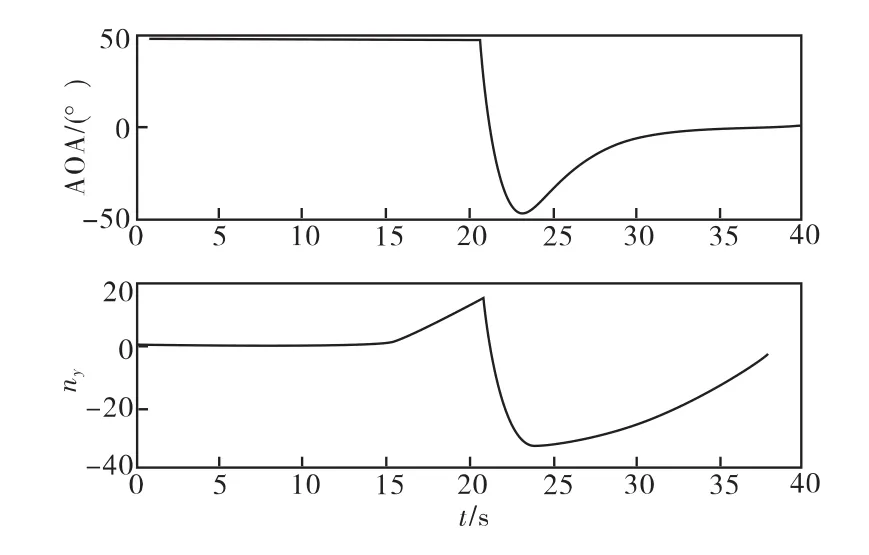
图6 攻角和过载
文中根据表1中所示再入速度和最小再入角的分布情况,通过拟合关系式(17)得到再入速度和最小再入角边界的近似分布,如图7所示。


图7 拟合最小再入角边界及可行区域
图7中虚线右下方区域是弹头再入过程中,满足过载约束、攻角约束、命中速度、命中倾角和命中精度的可行区域。为了进一步验证该曲线和可行区域的正确性,同时研究再入速度和再入倾角对动能弹终端命中参数的影响,文中开展了以下研究。
2.2 再入速度与再入角影响
从表1可知,边界点上的再入参数能够保证各种约束下弹体命中目标,但命中速度不高,而动能弹的目的就是要最大限度的提高命中速度。因此,文中以7 000 m/s的再入速度,-23.8°的再入角为基本标准,依次研究再入角一定、再入速度变化和再入速度一定、再入角变化两种情况下满足最大命中速度的参数优化问题。
通过计算得到不同情况下再入参数和命中参数如表2和表3所示。从表2中不难发现,当再入速度7 000 m/s,再入角 -22.8°时,弹体获得最大命中速度为1 940 m/s,而这一点正好位于图7所示边界曲线上方的不可行区。随着再入角往边界曲线的下方移动,逐渐转入可行区域,而且随着再入角的下移,目标距离缩短,命中速度逐渐提高。而从表3中所示参数的变化情况可知,当再入速度6 500 m/s,再入角 -23.8°时,弹体能够获得的最大命中速度为1 920 m/s,该点正好位于图7中边界曲线左侧的不可行区。随着命中速度向边界曲线的右侧移动,逐渐进入可行区域,目标距变化并不大,基本在(165±5)km范围内,但命中速度却有明显提高。
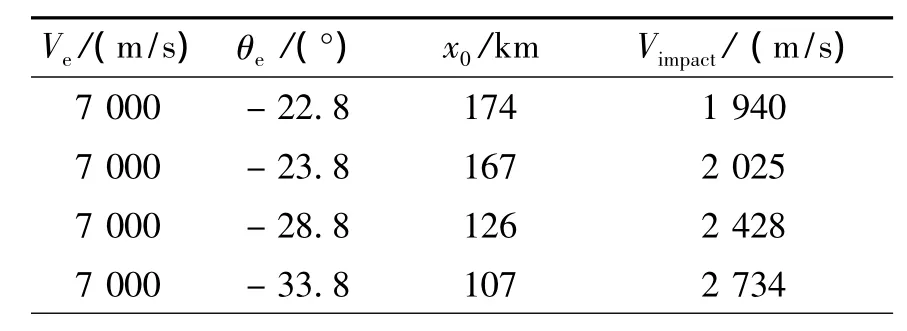
表2 不同再入角对应的最大命中速度对比

表3 不同再入速度对应的最大命中速度对比
3 结论
文中通过制导律与状态参数之间的代数关系,将包含控制量的动能弹微分方程组转化为由状态参数表示的代数方程组,利用序列二次规划法求解最优参数问题。全文研究结果证明了两点:
1)通过文中设计的计算方法获得的再入速度和最小再入角边界曲线及可行区域分布图是可信的,也证明了文中采用的参数优化方法是可行的;
2)明确了再入角和再入速度对命中速度的影响,与增加再入角来提高命中速度相比,增加再入速度不但能够增加动能弹的命中速度而且还能够尽可能减小离轨制动时的燃料消耗。
[1]Bob P,Michael M,Calvin S,et al.Space weapons earth wars,AD -A403411[R].
[2]黄国强,南英,陈芳,等.无动力滑翔弹最优抛射初始条件研究[J].飞行力学,2009,27(1):93-95.
[3]WestW J.Developmental testing of a laser-guided bomb simulation,AIAA 2008 -1629[R].2008.
[4]张煜,张万鹏,陈璟,等.基于Gauss伪谱法的UCAV对地攻击武器投放轨迹研究[J].航空学报,2011,32(7):1240-1251.
[5]Wilson S A,Vuletich I J,Fletcher D J,et al.Guided weapon danger area and safety template generation a new capability,AIAA 2008 -7123[R].2008.
[6]Siewert V L,Sussingham JC.6-DOF enhancement of precision guided munitions testing,AIAA 1997 - 5522,[R].1997.
[7]Anhtuan D N,David B D.Footprint determination for reusable launch vehicles experiencing control effector failures,AIAA 2002-4775[R].2002.
[8]雍恩米.飞行器轨迹优化数值方法综述[J].宇航学报,2008,29(2):397 -406.
[9]侯明善.防区外投放制导炸弹滑翔段垂直面最优制导[J].兵工学报,2007,28(5):572 -575.
[10]Elnagar G,Kazemi M A,Razzaghi M.The pseudospectral legendremethod for discretizing optimal control problems[J].IEEE Transaction on Automatic Control,1995,40(10):1793-1796.
[11]Hull D G.Conversion of optimal control problems into parameter optimization problems[J].Journal of Guidance,Control,and Dynamics,1997,20(1):57 -60.
[12]Hargraves CR,Paris SW.Direct trajectory optimization using nonlinear programming and collocation[J].Guidance,Control and Dynamics,1987,10(2):338 -342.
[13]赵汉元.飞行器再入动力学和制导[M].长沙:国防科技大学出版社,1997:214-238.
[14]Edward R Hartman,Patrick J Johnston.Mach 6 experimental and theoretical stability and performance of a cruciform missile at angles of attack up to 65°[R].NASA Technical Paper 2733,1987.
[15]Christopher L Darby,William W Hager,Anil V Rao.A preliminary analysis ofa variable-order approach to solving optimal control problems using pseudospectral method[C]//Astrodynamics Specialist Conference,2010,AIAA 2010-8272.

