尺寸效应对钢筋混凝土桥墩抗震性能影响的试验研究
李 徐,钟铁毅,夏 禾
(北京交通大学 土木建筑工程学院,北京 100044)
对于钢筋混凝土桥梁结构,使桥墩在地震作用下发生预期的弯曲延性,是保证桥梁在强震作用下具备足够耗能能力和预防倒塌的重要方法。为能合理计算和控制桥墩延性能力,国内外学者进行了大量研究,其中,由于钢筋混凝土墩柱非线性破坏过程受许多复杂因素影响,模型试验成为研究结构抗震性能和破坏机理的重要手段。然而,在实际试验进程中,受试验设备和经费的限制,常需要对原型桥墩进行缩尺,即以小比例的模型试件作为代替,在模型上施加相似力系,再根据相似条件,由模型试验的结果推演原型结构的抗震性能。这便使得在抗震试验结果的解释和推广中,模型相似理论变得尤为关键。
钢筋混凝土结构的缩尺模型由于制作误差、材料的力学性能、混凝土自身缺陷影响的裂缝形态以及纵筋滑移等复杂非线性行为,造成缩尺模型与原型结构结果差异,称为尺寸效应。国内外学者针对混凝土结构尺寸效应问题的研究已有部分成果,Bazant[1-2]根据断裂力学及弥散裂缝理论,研究了无筋素混凝土结构强度受尺寸变化的影响规律;Wu等[3]进行了3个不同缩尺比例轻骨料混凝土梁的拟静力试验,结果表明模型尺寸的增大将提升梁体屈服弯矩和极限弯矩;Choudhury等[4]针对尺寸效应对钢筋混凝土梁柱节点性能的影响进行了试验研究,结果表明梁柱节点的单位体积累计耗能受尺寸影响明显,小尺寸模型展现更好的延性;Carpinteri[5]利用混凝土裂缝结合力模型和叠加模型,结合试验,研究了钢筋混凝土梁体尺寸大小对其转动延性能力的影响;Sasaki[6]进行了不同缩尺比例的钢筋混凝土短柱模型试验,研究了墩柱抗剪强度受尺寸效应影响规律。
虽然针对尺寸效应的研究已获得部分成果,但研究的结构形式多为梁体,桥梁墩柱结构的研究可查询资料很少;多数研究成果显示钢筋混凝土结构的位移延性受模型尺寸影响明显,但均未见给出合理的反演关系。本文通过二个符合相似关系的桥墩模型拟静力试验,对比分析了尺寸效应对钢筋混凝土墩柱各项性能参数的影响,根据简化曲率分布模型和纵筋滑移模型,推导给出桥墩模型试验中墩顶水平极限位移的建议反演方法。
1 试验概况
1.1 试验设计
本试验采用量纲分析的方法得到模型试验的相似关系,试验采取拟静力加载方式,为结构静力相似问题,与结构静力问题有关的主要物理量有:① 结构的几何尺寸;② 静荷载,如集中力P、线荷载W、面荷载Q以及弯矩M;③ 结构效应,如线位移x、转角θ、应力σ、应变ε;④ 材料性能,如弹性模量E、剪切变形G、泊松比υ、密度ρ。在量纲分析法中,绝对系统的基本量纲为长度[L]、时间[T]和力[F],依此可以求得结构静力试验模型与原型的相似关系,如表1所示,其中SL和Sσ分别代表模型的长度和材料应力相似常数。
由表1中第(4)栏,理想模型要求混凝土、钢筋等材料与原结构也具有相似成比例关系的σ-ε曲线,这在实际中难以满足,在现实模型试验中,通常采用与原结构相同的混凝土和钢筋材料,此条件下各参量的相似常数如表1中(5)栏所示,可以看出,除了模型材料密度难以满足1/SL的相似比例,其余物理量在实际中均易于实现,但需要指出的是,由于试验采用拟静力加载,结构动力效应可以忽略,因而受材料密度影响的结构惯性力接近于零,故认为采用此类相似条件进行模型设计是合理的。
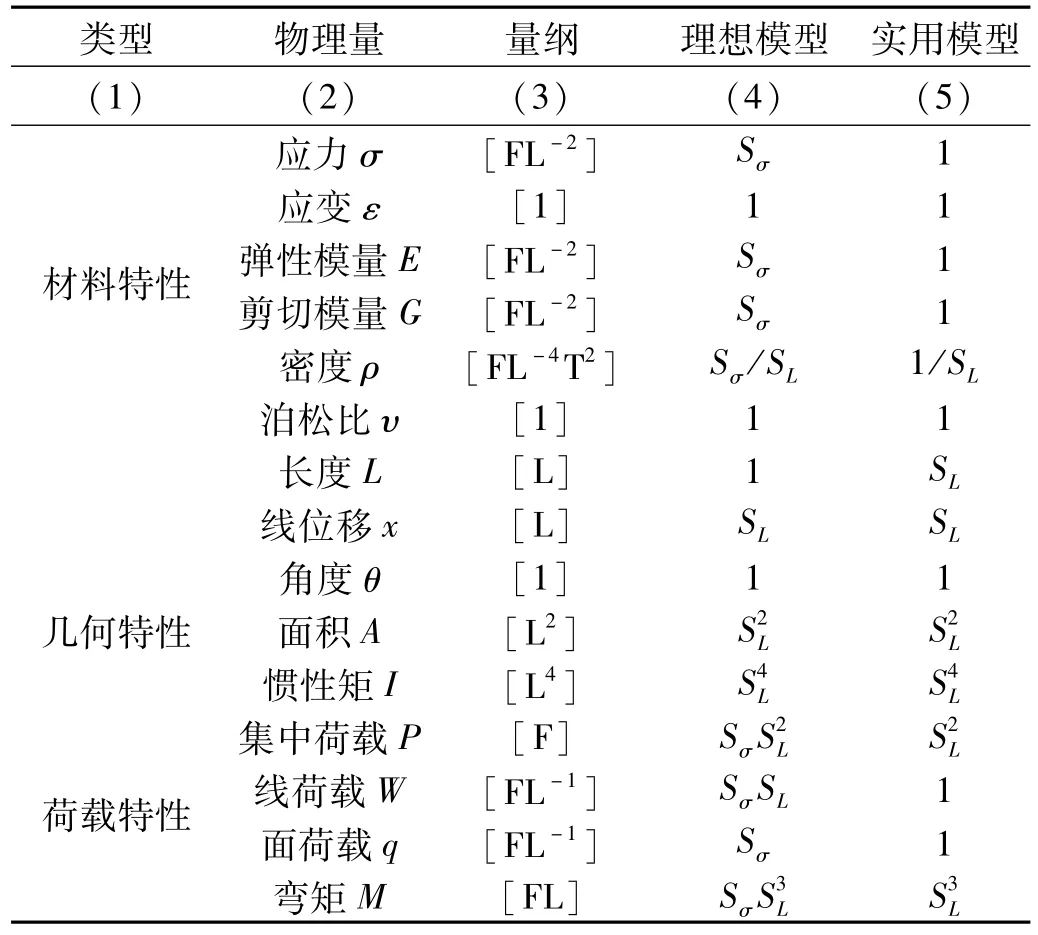
表1 结构静力试验模型相似常数Tab.1 Scale factors for static RC testing
根据上述模型相似关系,依据当前钢筋混凝土桥梁中独柱式桥墩的特点,设计进行了二个具有相似关系的矩形截面桥墩拟静力实验,其中试件P-1作为原型桥墩,墩高4.17 m,截面尺寸为 0.67 m×0.77 m,试件P-2为比例为3/4的缩尺模型,墩高3.07 m,截面尺寸0.50 m×0.58 m。两试件均采用标号为C40的混凝土,最大骨料粒径为20 mm,墩柱与基座整体浇筑制作,纵筋采用HRB400带肋钢筋,箍筋采用HPB235光圆钢筋,两试件纵筋率和配箍率一致。摸型的具体细节设计及参数如图1和表2所示。

图1 桥墩试件细节设计图Fig.1 Structural details of specimen

表2 模型参数Tab.2 Details of specimens

表3 试件延性性能Tab.3 Ductility parameters of specimens
1.2 加载方式和传感器布置
加载设备及传感器布置如图2所示,竖向荷载通过单向液压作动器一次加载到位,作动器顶部安装滚动支座,以保证作动器随试件水平位移移动,水平荷载采用MTS拟动力试验机施加。传感器的布置则包括:① 采用作动器上的行程传感器测量墩顶水平位移和荷载;② 在底座两端分别布置竖向和水平位移传感器,以修正基座转动对试验结果的影响;③ 在桥墩两侧塑性铰区域内,沿墩高布置线性差动式位移传感器(LVDT),以得到桥墩墩底滑移及截面曲率特性;④ 在试件平行于加载方向的侧面的塑性区域内,布置两组线性差动式位移传感器(LVDT),测量墩柱剪切变形量。

图2 加载装置及传感器布置图Fig.2 Test set up
试验加载模式如图3所示,横向往复荷载采用位移加载模式,试件屈服前以一毫米为增量逐级加载,试件屈服后以屈服位移为增量加载,每级加载循环三次,直至试件抗力下降至最大抗力的80%时,定义试件破坏,试验终止。
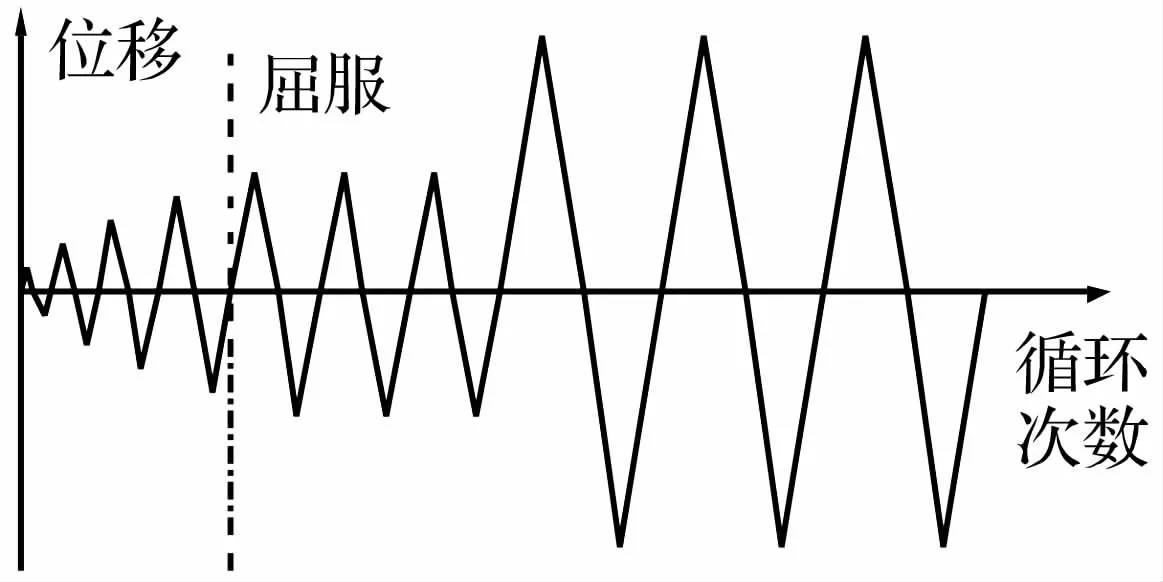
图3 加载模式Fig.3 Loading cycles
2 试验结果分析
在模型试件试验加载进程中,随着荷载等级增加,混凝土表层首先产生微裂缝,接着,纵筋屈服,裂缝开展变大,表层混凝土出现剥落,塑性铰开始在墩底产生;进一步加大荷载,纵筋屈曲,箍筋屈服;接着核芯混凝土压碎,纵筋断裂,承载力下降20%以上,试件破坏,整个过程呈现为典型的弯曲破坏模式。桥墩试件的实测延性性能参数如表3所示。
为了研究尺寸效应对钢筋混凝土矩形墩力学行为的影响,分别从试验实测的墩顶力-位移曲线、墩底塑性区截面弯矩-曲率曲线、墩顶纵筋滑移、能量耗散等角度对试件P-1和P-2进行比较研究。
2.1 墩顶水平力-位移骨架曲线比较
本试验通过墩顶外接位移计及试验机内置测力传感器,测量得到了两试件墩顶力-位移滞回曲线,如图4所示。图中标出了纵筋屈服、混凝土剥落及纵筋屈曲等关键破坏状态的位置。为了更好的描述构件的延性性能,图中同时用试件墩顶水平位移和无量纲的横向漂移率(漂移率=水平位移/墩高)来表示结构的变形能力。
为研究尺寸效应对结构水平抗力及延性的影响,取图4两试件滞回曲线的外包络骨架线进行比较,如图5所示,其中横坐标为墩顶横向漂移率,而纵坐标则根据模型的尺寸比例,将墩顶水平抗力依相似关系按式(1)进行转换:

式中:Pse为P-2试件按比例系数反演的水平抗力;Ps为P-2试件的实测墩顶水平抗力;SL为比例系数(=4/3)。
通过图5对两试件力-位移骨架曲线的比较,可以看出,两曲线在前期的弹性段几乎重合,且缩尺模型P-2反演得到的峰值水平抗力与原型桥墩P-1十分接近,差异仅在5%以内,但是,最终破坏时模型P-2的极限漂移率却比P-1大24%。这说明,在利用模型试验反推原型桥墩的性能时,原型桥墩的水平抗力能力可以被较好的评估,但延性能力却可能被过高估计而带来不安全隐患。
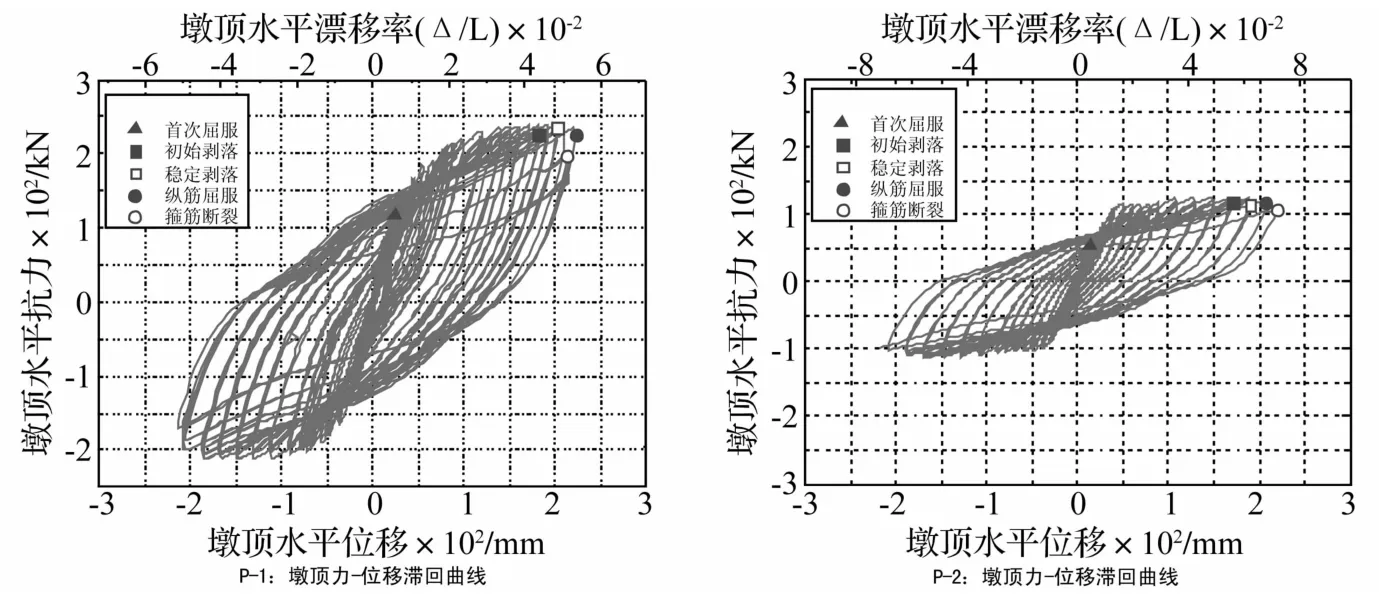
图4 试件力-位移滞回曲线Fig.4 Lateral load response of test specimens
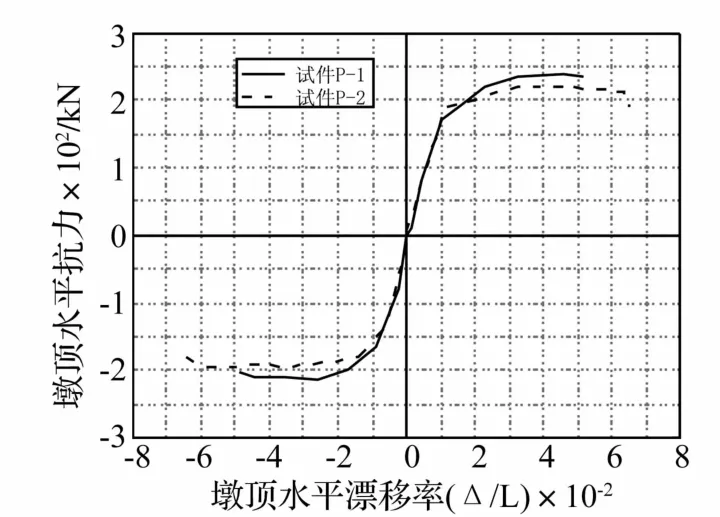
图5 力-位移骨架曲线比较Fig.5 Contour of force-displacement hysteresis loops
2.2 墩底截面弯矩-曲率骨架曲线比较
本试验预先在墩柱塑性区两侧植入曲率杆,各曲率杆之间以及曲率杆与基座之间用位移传感器相连,以测试其竖向变形,如此,便可得到每根曲率杆的转角,进而得到所测长度范围内的平均曲率,最终得到桥墩底部塑性区截面的弯矩-曲率关系,如图6所示:
为了研究尺寸效应对墩底塑性区截面弯矩抗力及曲率延性的影响,对两试件弯矩-曲率滞回曲线的外包络骨架曲线进行比较,如图7所示,其中横坐标为无量纲的曲率延性系数,纵坐标则根据模型尺寸比例,将截面抵抗弯矩按式(2)进行转换:

式中:Mse为P-2试件按比例系数反演的墩底截面弯矩;Ms为P-2试件的实测墩底截面弯矩;SL为比例系数(=4/3)。

图6 试件弯矩-曲率滞回曲线Fig.6 Moment-Curvature Hysteretic response of test specimens

图7 墩底截面弯矩-曲率骨架曲线比较Fig.7 Contour ofmoment-curvature hysteresis loops
由图7可以看出,从截面层次的角度,试件P-1和P-2不论是截面抵抗弯矩还是曲率延性均很接近,墩底塑性区截面无论是强度能力还是延性能力的反演均基本符合比例系数关系,这与之前的结构力-位移骨架曲线对比得到的结论不同,说明从二维截面层次分析,尺寸效应对截面弯矩-曲率关系的影响不显著。可以进一步推断,在力-位移曲线反演中试件墩顶水平极限位移的差异可能由粘结滑移、纵筋受压屈曲等结构三维因素影响造成。
2.3 滑移位移分量比较
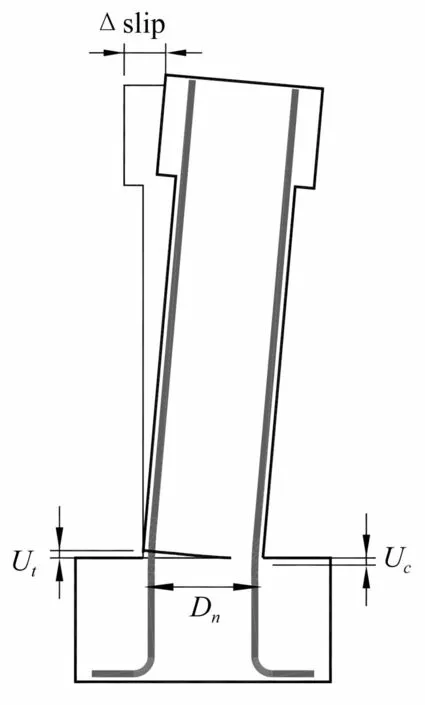
图8 悬臂墩滑移位移示意图Fig.8 Slip displacement of cantilever column
本试验中,为测量墩底滑移位移,在墩身两侧靠近基础的位置布置曲率杆,并在曲率杆与基座之间用位移传感器相连,以测试其在加载历程中竖向变形,如图8所示。图中:Δslip为纵筋滑移引起的墩顶水平位移;Dn为截面两侧纵筋中心间距;ut和uc分别表示纵筋滑粘结移造成的墩柱受拉侧及受压侧的竖向位移,由曲率杆与基础间位移计测量得到。依据图8,得到式(3)计算纵筋滑移引起的墩顶水平位移:
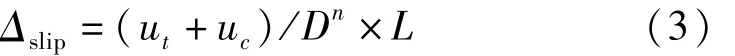
为了比较试件P-1和P-2的墩顶水平位移中滑移分量受尺寸效应的影响,根据试验实测两墩柱滑移位移,以无量纲的墩顶水平漂移率为横坐标,Δslip/Δtip为纵坐标,绘于图9:

图9 纵筋滑移引起墩顶水平位移分量比较Fig.9 Lateral displacement due to bond slip of longitudinal bars
由图9可以看出,试件P-2的滑移分量所占比重始终高于P-1桥墩,这其中原因是纵筋滑移量的大小主要受纵筋直径和混凝土强度影响[7],而在实际试验进行模型比例缩小时,很难做到处处精准的符合比例关系,对于P-1和P-2两个试件,为了保证两者配筋率一致,选取的钢筋标号一致,纵筋直径没有符合3/4比例系数的关系,造成了在试件混凝土强度一致的情况下,两者墩底纵筋滑移相当,致使P-2桥墩墩顶位移中滑移分量的比重相对更大,这也进一步成为试件P-2的墩顶水平漂移率大于试件P-1的原因。
2.4 能量耗散比较
桥墩的滞回耗能特性反映了桥墩耗散外来能量以抵抗地震力的能力,这对于桥梁延性抗震设计尤为重要。桥墩的滞回耗能定义为力-位移滞回曲线中封闭滞回环包围的面积,滞回环面积越大,桥墩的耗能能力越强。
为了比较试件P-1和P-2在加载过程中的滞回耗能能力,根据图4的两试件力-位移滞回曲线求出各自滞回耗能(滞回环面积)与自身位移加载历程的关系,再根据相似原理,将耗能能力按式(4)进行比例转换。且为了便于比较,横坐标的位移加载历程采用无量纲的水平漂移率表示,如图10所示。

其中:Wse为P-2试件按比例系数反演的滞回耗能;Ws为P-2试件的实测滞回耗能;SL为比例系数(=4/3)。

图10 滞回耗能比较Fig.10 Comparison of energy absorption
由图10可以看出,试件P-1和P-2具有相似形状的耗能曲线:在前期的弹性阶段耗能很小,随着塑性延性的稳定发展,滞回耗能也持续增加,直到纵筋由于过大位移发生屈曲和断裂,导致耗能曲线在后半段发生下降。
由图10,试件P-2在同等的墩顶横向位移漂移率时耗能低于P-1,产生这个现象的可能原因有两个:①试件P-2的墩顶水平总位移中滑移分量比重较大,而纵筋滑移是使滞回曲线出现反S形的主要因素之一,对结构耗能帮助很小;② 由图5所示的两试件墩顶力-位移骨架曲线,虽然试件P-1和P-2的水平抗力很接近,但P-1仍略高一些,耗能为力-位移滞回曲线的包络面积,则P-1的计算耗能相对更大。
3 墩柱位移延性反演关系推导
由前述试验结果的分析比较可知,试件P-1和P-2具备几乎一致的水平抗力,但试件P-2却由于基底纵筋粘结滑移的影响,墩顶水平位移包含更多滑移位移分量,因此,需妥善考虑墩顶水平位移受尺寸效应的影响。
根据试验实测记录,墩顶水平位移主要由剪切位移、弯曲位移和墩底滑移位移构成,可写成式(5)形式:

式中,Δu为墩顶极限位移,Δv为剪切位移,Δb为弯曲位移,Δs为滑移位移。
值得注意的是,此次试验研究的试件P-1和P-2的剪跨比高达6.2,根据试验现象和测量数据的记录,试件发生明显的弯曲主导破坏,剪力引起的水平位移分量所占比例很小,这与其他学者试验研究成果相一致[8],故认为对于弯曲主导破坏桥墩:

墩顶弯曲位移Δb与桥墩曲率分布之间存在如下关系[9]:

根据试验,在墩底截面达到极限状态时,其弯矩-曲率骨架曲线如图11(a)所示,由此可转换得到沿墩高的实际曲率分布曲线,如图11(b)。为便于计算,通常根据等能量原则将截面弯矩-曲率曲线简化为双线性[10],由此沿墩高的曲率分布曲线也可简化为双线性,如图 11(c)所示:

图11 墩身曲率分布图Fig.11 Curvature distribution along column length
根据图11和式(7),进行积分计算,可以得到墩顶弯曲位移如下所示:
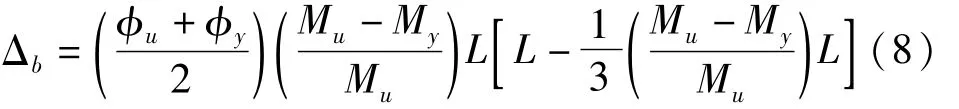
式中,My为截面屈服弯矩,Mu为截面极限弯矩,Фy为截面屈服曲率,Фu为截面极限曲率,L为墩高。
由纵筋滑移产生的墩顶位移Δs则主要受纵筋直径、纵筋强度和混凝土强度等因素影响,根据Sezen等[7]提出的滑移力学模型,如图12,墩顶滑移位移可依据下式计算:

式中,db为纵筋直径,f′c为混凝土抗压强度,Фy为截面屈服曲率,Фu为截面极限曲率,fy为纵筋屈服强度,fu为纵筋极限强度。
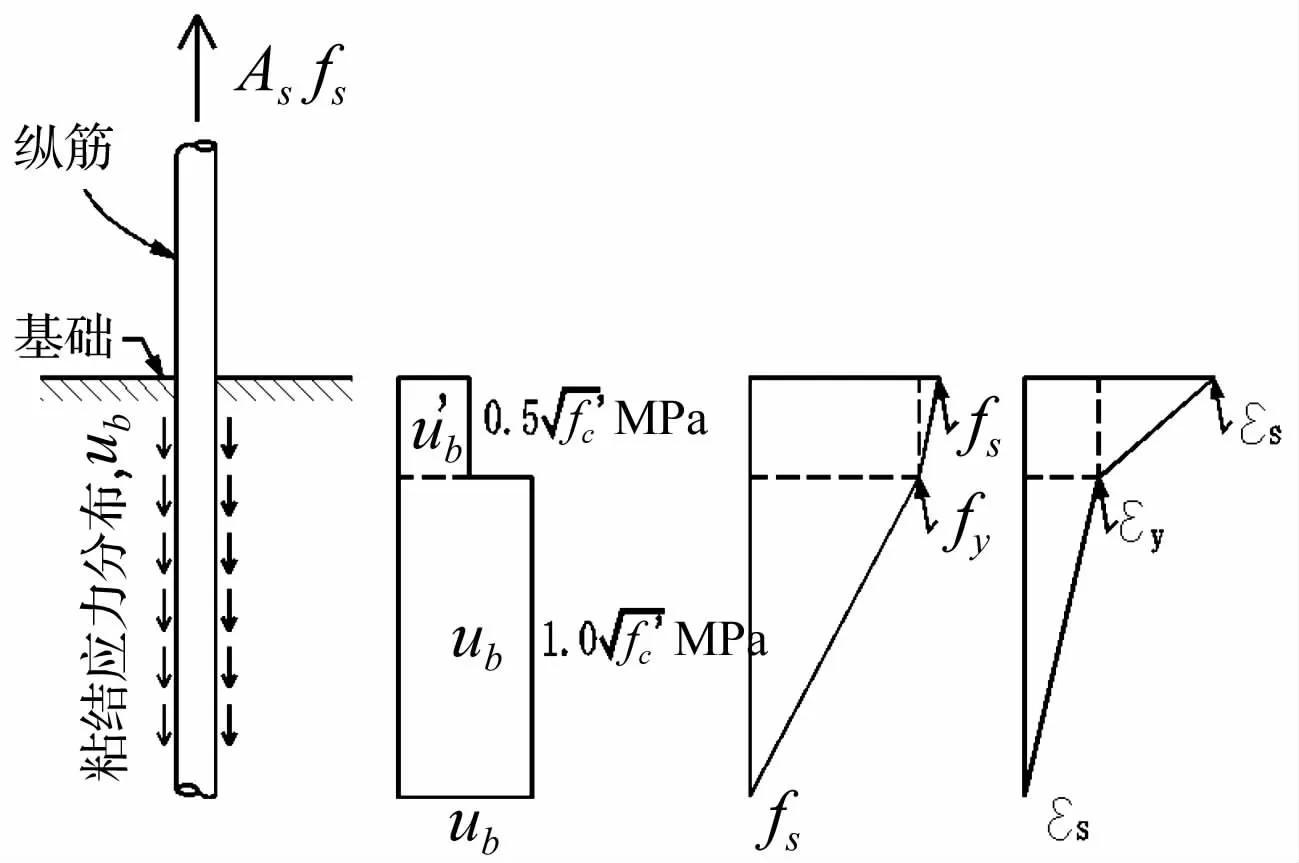
图12 纵筋滑移力学模型Fig.12 Proposed reinforcement slip model
由式(6)、式(8)和式(9),经过合并和简化,得到桥墩墩顶水平位移的计算式:
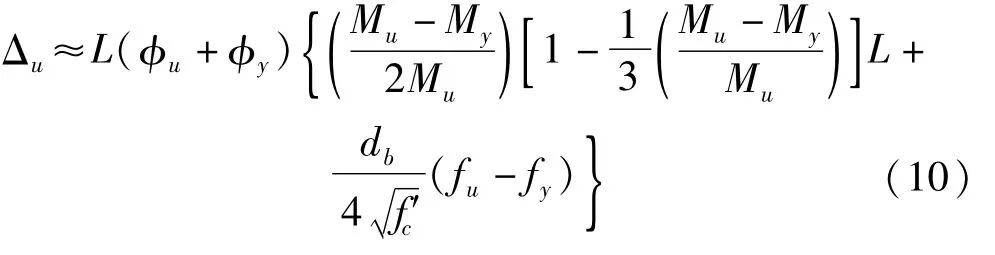
令将式(10)写成如下形式:
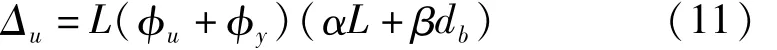
为推导模型试验中墩顶水平位移的合理反演关系,定义原型桥墩墩顶水平位移为Δu,缩尺模型墩顶水平位移为Δ′u,则桥墩的实际墩顶水平位移比例关系S′L为

在式(12)中,根据试验结果,原型桥墩与缩尺模型的截面曲率延性符合比例关系,墩高和曲率延性的量纲互为倒数,因此L′(φ′u+φ′y)=L(Фu+Фy);原型桥墩与缩尺模型的截面抵抗弯矩符合比例关系,对于特定桥墩,可视作定值,因此α′=α;原型桥墩与缩尺模型采用相同材料性能的钢筋及混凝土常数,因此β′=β。故可得:

依据式(13),即可由模型试验的材料参数和实测数据,计算出考虑缩尺效应下的模型试件和原型桥墩间墩顶水平位移反演关系。
为分析不同缩尺比例系数SL下墩顶水平位移的反演差异,定义位移比例差异性系数ζ=S′L/SL,以试件P-1、P-2为研究对象,结合式(13),得到ζ随SL的变化关系如图13所示:

图13 不同缩尺系数下模型极限位移反演差异Fig.13 Ultimate displacement capacity verse scale factor
由图13,当模型的缩尺比例系数小于一定值时,其对墩顶极限位移反演带来的差异性呈几何数增长,在这种情况下,若没有妥善考虑尺寸效应的影响,将过高估计结构延性,带来不安全隐患。这也对模型试验提出指导,在满足经费和试验设备的条件下,尽可能的采取较大比例的缩尺模型,将得到更真实的位移延性结果。
在图13中,将作为原型桥墩的试件P-1,及缩尺系数为3/4的试件P-2分别在图中标出,可以看出,根据式(13)推导的计算结果曲线是与实测值接近的,当然,受试验试件数量限制,在将来当进行更多样本试验进行验证和校对。
综上,对于弯曲主导破坏的桥墩,在保证模型试件材料特性与原型结构一致的情况下,按相似关系设计的模型,墩顶水平抗力的反演基本符合比例关系,但由于钢筋直径、骨料级配箍筋间距等细部没能做到精确符合比例关系,纵筋滑移的三维复杂效应对结构极限位移产生较大影响,式(13)为模型桥墩的合理反演提供了一个解决思路,具备一定参考价值。
4 结 论
通过钢筋混凝土桥墩力学行为受尺寸效应影响的试验及理论研究,得出以下结论:
(1)试件墩顶水平抗力、墩底截面抵抗弯矩和截面曲率延性基本符合相似关系,尺寸效应对结构承载力和二维截面弯矩-曲率关系无显著影响;
(2)受基底纵筋粘结滑移影响,模型试件墩顶水平位移中滑移位移分量较大,在墩顶位移延性反演中需妥善考虑;
(3)受基底纵筋粘结滑移影响,同等墩顶水平漂移率下,缩尺模型试件结构耗能偏低;
(4)模型试验中由于钢筋直径等细部难以精确符合比例关系,对墩顶水平极限位移反演时可参考式(13)进行。
[1]Baziant Z P.Size effect on structural strength:a review[J].Archive of Applied Mechanics,1999,69(9-10):703-725.
[2]Baz?ant Z P.Size effect[J].International Journal of Solids and Structures,1999,37(2000):69-80.
[3]WU Chung-hao,KAN Yu-cheng,HUANG Chung-ho,et al.Flexural behavior and size effect of full scale reinforced lightweight concrete beam[J].Journal of Marine Science and Technology,2011,19(2):132-140.
[4]Choudhury A M,Dutta A,Deb SK.Study on size effect of retrofitted beam-column jointwith beam weak in flexure under cyclic loading[C]//35th Our World In Concrete&Structures.Singapore.2010.25-27.
[5]Carpinteri A,Corrado M,ManciniG,et.al.Size scale effect on plastic rotational capacity of reinforced concrete beams[J].ACIStructural Journal,2009,106(6):887-896.
[6]Sasaki T,Kawashima K.Scale effect on the shear strength of reinforced concrete columns with termination of main reinforcements[C]//3rd International Conference on Advances in Experimental Structural Engineering.San Francisco.2009.1-11.
[7]Sezen H,Setzle E J.Reinforcement slip in reinforced concrete columns[J].ACI Structural Journal,2008,105(3):280-289.
[8]Restrepo J R,Seible F,Bernd Stephan,et.al.Seismic testing of bridge columns incorporating high-Performance materials[J].ACI Structural Journal,2006,103(4):496-504.
[9]李徐,钟铁毅,夏禾,等.轴压下钢筋混凝土桥墩塑性铰特性研究[J].中国铁道科学,2014,35(1):34-41.LI Xu,ZHONG Tie-yi,XIA He,et al. Study on the Characteristics of plastichingeof reinforced concrete pier under axial load[J].China Rallway Science,2014,35(1):34-41.
[10]江辉,慎丹,刘夏润,等.基于改进 Park-Ang模型的 RC桥墩地震动损伤及滞回耗能特性研究[J].振动与冲击,2012,31(5):97-105.JIANG Hui,SHEN Dan,LIU Xia-run,et al.Seismic damage and hysteretic energy dissipation characteristics of a RC bridge pier based on improved Park-Angmodel[J].Journal of Vibration Shock,2012,31(5):97-105.

