基于改进的自适应噪声消除和故障特征阶比谱的齿轮噪源干扰下变转速滚动轴承故障诊断
王天杨,李建勇,程卫东
(北京交通大学 机械与电子控制工程学院,北京 100044)
齿轮噪源是干扰滚动轴承故障诊断的常见因素。在时域上,幅值较大的齿轮振动会掩盖轴承故障带来的冲击特征;在频域上,则会影响对轴承故障引起的共振频带的获取。因此,对作为噪声的齿轮振动予以去除成为对滚动轴承进行故障诊断的前提[1]。针对这个问题,时域同步平均技术(TSA)、线性预测技术、适应性噪声消除技术(ANC)、自适应噪声消除技术(SANC)及其频域快速算法(DNS)均曾被用来去除齿轮噪源的干扰[2-3]。其中,除ANC外,其余算法均利用齿轮噪源的周期性对其进行去除。但是,当齿轮以变转速的模式运行,其周期性也会随之消失。而以上利用齿轮的周期性特征对其去除的算法也将失效。针对这一问题,可以将这些算法与阶比跟踪技术[4]相结合来弥补变转速带来的麻烦。具体可以利用转速计获取齿轮的转速信息,以等角间隔对时域非平稳信号进行重采样,在把齿轮部分转化为平稳信号的同时,恢复其周期性。这样因变转速工作模式而失效的齿轮噪源消除算法也将恢复作用。另外,适应性噪声消除技术因为采用额外的传感器拾取参考信号也能够用于变转速模式下的齿轮噪源去除。然而,这两种算法均对辅助设备有所依赖。其中,ANC算法利用在特定位置加装振动传感器拾取参考信号;利用阶比跟踪技术的改进算法则需要转速计获取键相信号对齿轮的转速进行估计。对于前者,参考传感器的位置对整个算法的效果影响很大:要求参考传感器尽量拾取只包含齿轮振动而不包含轴承振动的信号。这就要求传感器的位置尽量靠近轴承而远离齿轮。这样的位置在实际工程中是很难获取的(比如,齿轮箱中运行轴承的故障诊断);而对于后者,也常常由于安装空间与成本的制约,使得转速计的安装在实际工程中受到限制(同样限制参考传感器的应用)。
综上,本文试图在不使用辅助设备的前提下消除变转速下的齿轮噪源干扰,并完成滚动轴承的故障诊断。针对这个问题,可以利用基于时频分析的阶比跟踪技术[5]对齿轮的瞬时转频进行估计。理论上,当齿轮以匀速运转时,其对应频谱的啮合频率及其倍频上将出现明显的峰值,而其中幅值最大将是某个阶数未知的倍频。因此,该峰值与齿轮的转频之间存在固定但未知的比例关系。当转速随时间变化时,该最大值也将成比例变化进而形成一条与转速同步的趋势。为与齿轮转频相区分,本文将其命名为峰值啮合倍频(IDMH)趋势线。然而,该趋势线却不能代替文献[6]中的齿轮转频对原信号进行重采样并且在角域针对齿轮噪源进行去除。因为,在没有转速计的帮助下,需要依据去除齿轮噪源后的剩余信号进一步对轴承转频进行估计。而“角域重采样-齿轮噪源去除-反采样”的齿轮干扰去除算法必然会对本就微弱的轴承信号产生削弱,继而影响对轴承转频的获取。另外,由于峰值啮合频率与齿轮转频的比例未知,也不能根据IDMH趋势线直接获取滚动轴承的转频。
为此,本文提出基于改进的自适应噪声消除技术和故障特征阶比谱的算法实现不依赖辅助设备的变转速下齿轮噪源去除和滚动轴承的故障诊断。首先,基于IDMH趋势线构造参考信号自适应地削弱齿轮噪源对轴承共振区提取的干扰;其次,利用谱峭度算法从自适应滤波结果中提取最能反映滚动轴承故障的频带并获取其包络信号;然后,利用峰值提取算法从包络滤波信号的时频分析结果中对瞬时故障特征频率(IFCF)趋势线进行提取;最后,利用IFCF趋势线对基于谱峭度的滤波结果进行故障阶比域重采样,并利用重采样信号的故障特征阶比谱判断滚动轴承的运行状态。
1 算法部分
1.1 改进的适应性噪声消除算法
ANC算法可用于分离混合信号中两个不相关的成分,而其成功的前提是参考信号中须尽量仅与其中一个信号成分相关。其算法原理如图1所示。
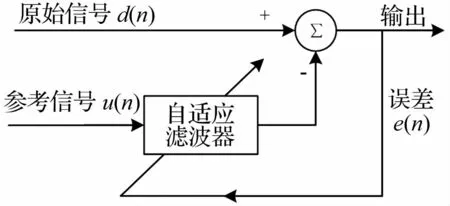
图1 适应性噪声消除算法原理图Fig.1 The schematic diagram of ANC
具体的,原始信号包含故障轴承振动信号与齿轮啮合振动信号两个不相关的分量。在理想的情况下,参考信号应尽量只与原信号中齿轮成分相关。整个算法通过自适应调整滤波器的权值使得原信号d(n)与滤波器的输出信号y(n)的误差e(n)的均方值最小。在参数调整的过程中,使自适应滤波器的性能无限接近最优。自适应滤波器的输出即为对周期性齿轮噪源的估计;它与原始信号之差则为轴承部分。ANC的具体算法和参数选择策略可参见[7]。
但是,最优参考传感器位置的难以确定将制约着该方法的应用。而上文提出了IDMH趋势线正是齿轮噪源对轴承故障共振频带的获取产生干扰的主因。因此,利用该趋势线构造的参考信号应满足仅包含齿轮噪源的要求。基于以上分析,本文提出基于IDMH趋势线构造参考信号以改进ANC算法用于对齿轮噪源干扰的削弱。其具体算法如下:
首先,利用短时傅里叶变换(式(1))获取原混合信号的时频分析结果,并利用峰值搜索算法提取ti时刻对应的瞬时频谱STFT(ti,Ω)的最大值:瞬时峰值啮合倍频IDMHti。该最大值随时间的变化曲线即为ID-MH趋势线。
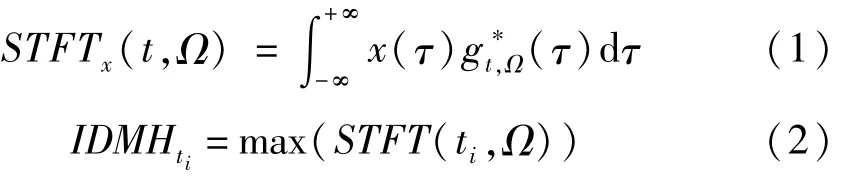
其中,g(τ)为窗函数。
其次,利用IDMH趋势线构造变频三角函数作为参考信号。其瞬时频率由IDMH趋势线的三次多项式拟合结果确定;其幅值则由以下算法确定:① 以IDMH趋势线对原始信号进行重采样(具体算法见1.4)。②由于齿轮啮合振动的原因,可以在重采样信号的频谱中找到突出的啮合倍频峰值(DMH)。该峰值的幅值即可作为参考信号的幅值ADMH。因此,参考信号可以表达为:
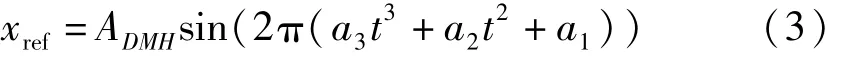
其中,a3,a2,a1为对应三阶多项式的系数。
最后,以式(3)为参考信号;以振动信号为原始信号,利用适应性噪声消除技术对齿轮噪源进行一定程度上的削弱。事实上,IDMH趋势线并不是齿轮噪源带来的所有干扰。所以,以它为基础构造的参考信号并不能起到完全去除齿轮噪源的作用。但是,也正因为其只是齿轮噪源的一部分,以它为参考信号的ANC算法不会影响到本就在幅值上处于弱势的轴承部分。这将有利于后续对轴承转频的提取。
1.2 基于kurtogram与STFT的滤波算法
由于改进的ANC算法削弱了齿轮噪源对故障轴承共振频带获取的干扰。本节利用谱峭度算法确定由轴承故障引起的共振所对应的中心频率,滤波带宽和尺度,并据此对自适应滤波结果进行二次滤波,获取冲击性最强的,最能反映轴承故障的包络滤波信号。作为时频域的四阶统计量,谱峭度[8]可以用来衡量冲击性在频域上的分布。该特性使其能够用于确定故障轴承引起的共振频带。信号 x(t)的谱峭度可由下式表示:其中表示平均值表示原信号在频率f处的复包络。如果信号的冲击部分集中于特定的频带,其对应滤波结果的峭度值将相对较大。谱峭度的计算方法有很多种:基于短时傅里叶变换的算法,基于小波变换的算法和基于快速kurtogram的算法。本文利用最后一种算法计算谱峭度。
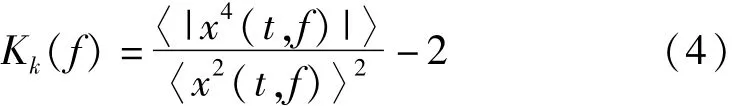
快速kurtogram算法是通过构建由准解析带通滤波器组成的树状滤波器组实现的。具体的,分别对原信号进行n级尺度的双子带分解和n-1级尺度的三子带分解。其中,三子带分解是的目的是为了获得更高的分析精度。因此,第i级尺度的三子带分解将被插到第i和第i+1级双子带之间。具体的算法如下:
首先,根据[9]中所述算法构建n级双子带和n-1级三子带树状滤波器组实现对原信号的2n-1级分解。
其次,利用式(4)计算各级尺度,各个频带滤波得到包络信号的峭度值 SK(fci,(Δf)k)。其中,fci为中心频率,(Δf)k为相应的滤波带宽。
最后,获取所有峭度值中的最大值,并利用对应的滤波参数获得滤波结果。其不但能最大程度上反映轴承故障信号部分,而且对应的时频谱比原始信号的时频谱也更清晰。
1.3 瞬时故障特征频率趋势线估计
根据上文的分析,由于IDMH趋势线和轴承的转频趋势没有确定的比例关系,所以不能根据它对滤波获得的轴承故障信号进行重采样。基于此,本节提出瞬时故障特征频率(IFCF)趋势线的概念代替轴承转频,并利用时频分析与峰值搜索算法对其进行提取。
理论上,若故障轴承以均匀转速运行,对应包络谱的故障特征频率处将出现明显的峰值。而故障特征频率仅与被监测轴承的几何参数和转频有关。不同的故障位置对应的不同故障特征频率可由式(5)~(7)唯一确定:
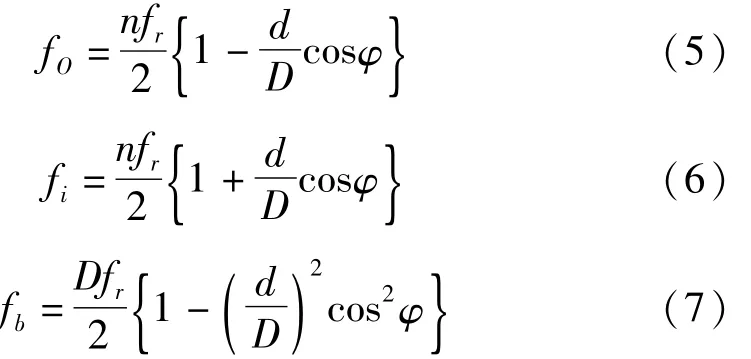
其中,n为钢球数;fr为的轴承转频;d是钢球直径;D是滚道节径;φ是接触角。
由以上公式可以看出,故障轴承对应的故障特征频率与轴承的转频之间有着固定的倍数关系。因此,若轴承转频随时间变化,其对应的故障特征频率也将随着之同步变化。本文将任意时刻瞬时包络谱中的故障特征特征频率命名为瞬时故障特征频率。与匀转速类似的是,瞬时故障特征频率在瞬时包络谱中也将具有幅值优势。这样,瞬时故障特征频率就成为了一个与转频存在固定倍数关系,并且能在瞬时包络谱中予以提取的物理量。上文中基于谱峭度得到的包络滤波信号为瞬时故障特征频率的提取提供了基础。具体的提取算法如下:
(1)利用STFT求得谱峭度滤波包络的时频包络谱。因为前两步滤波得到的是最能体现轴承故障的包络滤波信号,因此,该包络时频谱中将存在清晰的瞬时故障特征频率及其倍频。
(2)利用峰值提取算法,从包络时频谱(Envelope Time-Frequency Representation,ETFR)中对故障特征频率(IFCF)趋势线进行提取。
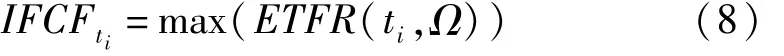
其中,ETFR(ti,Ω)为滤波包络的时频谱;IFCFti为 ti时刻的瞬时故障特征频率。其随时间变化组成的集合即为IFCF趋势线。它与轴承的转频同步变化,且有固定的倍数关系(对应的故障特征因子)。因此,可以代替转频,用于消除变转速对振动信号的影响。
1.4 基于采样频率重调的重采样算法
本节根据IFCF趋势线对两次滤波后的包络信号进行重采样。虽然IFCF趋势线与轴承的转频趋势同步变换并有着特定的倍数关系。但是基于IFCF的重采样与基于转频的重采样仍有明显的不同。因此,本文将基于IFCF趋势线的重采样信号所在的域称为故障角域,并提出一套不同的重采样策略:基于采样频率重调的故障角域重采样算法
与基于转频的角域重采样类似,基于IFCF趋势线的故障角域重采样也是以消除变转速对振动信号的影响为目的。传统的基于转频的角域重采样算法的实质是以等角增量对时域信号进行重新采样。实际上,该算法可以用一个更简单的策略进行描述:在转速相对较大的时间段用相对较高的采样频率,在转速相对较小的部分利用较低的采样频率。而采样频率间的比值应与对应转频的比值相等。
基于以上分析,本文提出基于采样频率重调的故障角域重采样算法。其具体算法如下:
(1)将滤波包络信号等分为n份,n与上文中求取的IFCF趋势线的长度相等。将每个子信号命名为x1,x2,…,xn,每个子信号对应着不同的 IFCF值:IF-CF1,IFCF2,…,IFCFn。
(2)定义基准采样频率和基准IFCF如下:
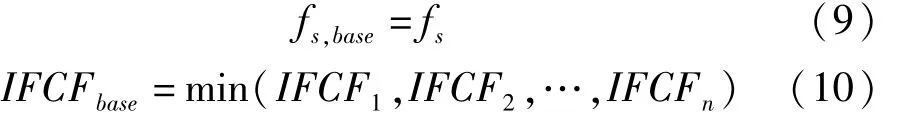
其中,fs为时域采样频率。
(3)利用不同子信号瞬时故障特征频率间的比值重新调整各子信号的采样频率:
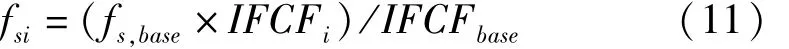
其中,IFCFi为第 i个子信号对应的瞬时故障特征频率。
(4)按照新求得的fsi对各子信号进行重新采样。具体的,首先利用各子信号对应的新采样频率重新确定采样点;其次以原始信号xi为基准,利用多项式拟合确定新采样点对应的重采样信号x′i;最后,将重采样信号x′i按照i的顺序排列,获得原信号的重采样信号:
因为IFCF趋势线与转频趋势线是同步变化的,所以不同时间点对应的转频之比与瞬时故障特征频率之比相等。因此,若应用基于采样频率重调的故障角域重采样算法对时域信号进行重采样,基于IFCF趋势线和基于转频重采样在效果上完全相同。
1.5 基于FCO谱的轴承故障诊断
在完成了故障角域重采样后,基于包络分析的故障诊断应该可以用与对滚动轴承的故障诊断。然而,仍有两个问题必须进行讨论:如何确定故障角域信号的等效采样频率;如何解释基于故障角域重采样信号获得的故障特征阶比谱。

根据fFPA,滤波包络冲采样信号对应的故障特征阶比谱(FCO)就可以利用FFT直接获取。
(2)对故障特征阶比谱的解释是对轴承运行状态判断的关键。本文通过它与依靠转频的重采样信号对应的阶比谱做类比,提出依据故障特征阶比谱的诊断策略。在角域中,重采样信号的包络谱被称为阶比谱。其横坐标为阶比,代表着转频。如果轴承含有故障,阶比谱中的故障特征阶比及其倍频上将出现明显的峰值。不同的故障位置(外圈,内圈,滚动体)对应着不同的特征阶比值:

其中,fo,fi,fb分别为外圈,内圈和滚动体故障对应的故障特征频率。fr轴承转轴的转频。若被监测轴承存在故障,对应的阶比谱中会在特征阶比及其倍频处将出现随阶比递减的峰值。
同理,在利用本文算法得到的故障特征阶比谱中也将出现类似的衰减的峰值。然而,本文在对滤波信号进行重采样时利用的是IFCF趋势线而并是转频趋势。因此,作为诊断依据的故障特征阶比谱与传统的角域阶比谱是不同的。故障特征阶比谱横坐标的物理意义是故障特征频率而非转频。实际上,利用本文算法得到的故障特征阶比谱是传统基于转频得到的阶比谱的等比压缩。其压缩比例因故障位置的不同而各异:外圈,内圈及滚动体故障的压缩比例恰为利用式13~15所得到的特征阶比值Oouter,Oinner和Oball。因此,阶比谱中的故障特征阶比将被统一压缩到1阶故障特征阶比处。因此,若滚动轴承含有故障,其故障特征阶比谱的1阶故障特征阶比及其倍频处就会出现表征故障的峰值。
2 仿真分析
为了验证本文提出的算法,本节构造升速模式下故障轴承和正常齿轮的变转速混合信号:
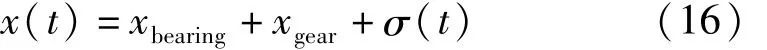
其中,xbearing代表故障轴承振动部分,xgear代表齿轮振动部分,σ(t)则代表白噪声部分。
变转速下的故障轴承信号xbearing的仿真公式为[10]的公式1b的改进版本:
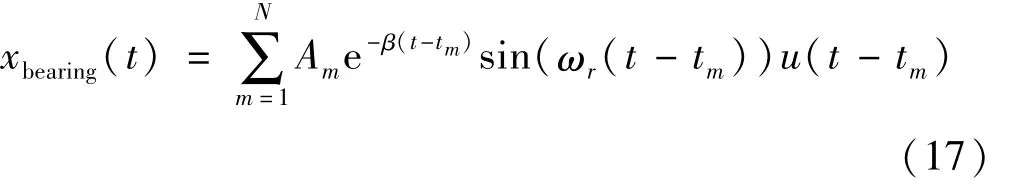
其中,Am=λtm为第m个冲击的幅值,本文将升速模式下轴承故障引起的冲击幅值与时间的关系简化为线性关系,λ为对应的比例系数;u(t)为单位阶跃函数;β为结构衰减系数;ωr为由轴承故障激起的共振频率,tm为第m个冲击发生的时间,可由以下递推公式确定:
陆游通过晚唐诗词的价值评骘,实际上导向了“诗词之辨体”;而其对晚唐诗词的矛盾价值观之张力影响也表露无遗:一方面是辨体、分体,在美学观念、审美理想上是尚理与重意、以善为美与以真为美的分野,一方面又局囿于词体“小道”的文类等级,徘徊、依违于审美与政教之两端。
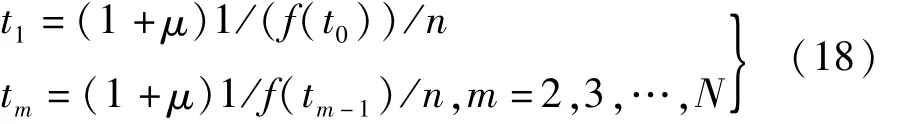
其中,f(t)为轴承转频随时间的变化规律;t0=0;μ为滚动体滑移误差系数,其取值范围为0.01~0.02;n为轴承每转出现的故障冲击数。
变转速下,健康齿轮振动的仿真公式如下:
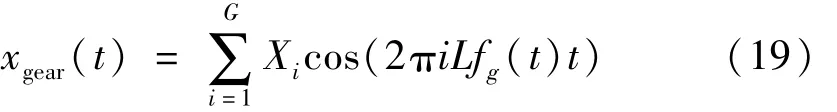
其中,i(1,2,…,G)为啮合频率谐波数;Xi为第 i阶谐波的幅值;L为齿轮的齿数;齿轮转频fg(t)与轴承转频的关系为:fg(t)=τf(t);Lfg(t)为齿轮啮合频率随时间变化的规律。
本文中,轴承转频随时间的变化规律设定为f(t)=2.5t+15;将齿轮啮合频率的二倍频设为峰值啮合倍频,啮合频率峰值X1设为0.1;二倍啮合频率X2设为1.2;三倍啮合峰值X3设为0.2。其他参数的具体取值见表1。
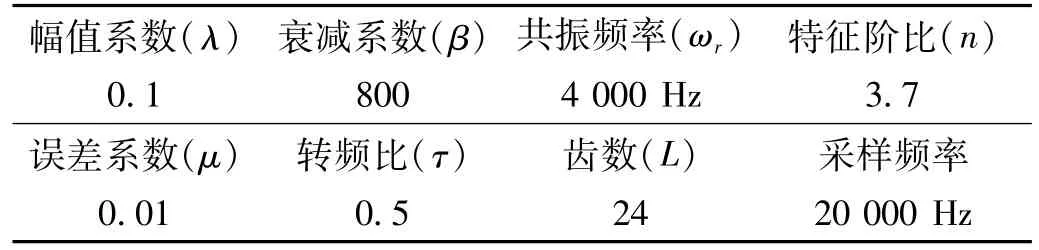
表1 仿真模型参数Tab.1 Parameters of simulated m odel
首先,利用改进的适应性噪声消除技术对齿轮噪源分干扰进行削弱。图2和图3分别为仿真混合信号的时域波形和对应的kurtogram图。从图3中我们可以发现在尺度7,中心频率为507 Hz处对应着最大的峭度值。而它恰好处于设计的齿轮峰值啮合倍频变化范围(360~600 Hz)之内。而并非设计的轴承故障共振频率(4 000 Hz)。这一现象直观地反映了齿轮噪源对轴承共振频率提取的阻碍。因此,我们试图利用改进的适应性噪声消除算法对这种干扰予以削弱。
其次,利用由谱峭度最大值所确定的滤波参数(见图5上部)对自适应滤波结果进行进一步滤波,获得最能反映轴承故障的包络信号并利用STFT获取如图6所示的滤波包络信号的包络时频谱。
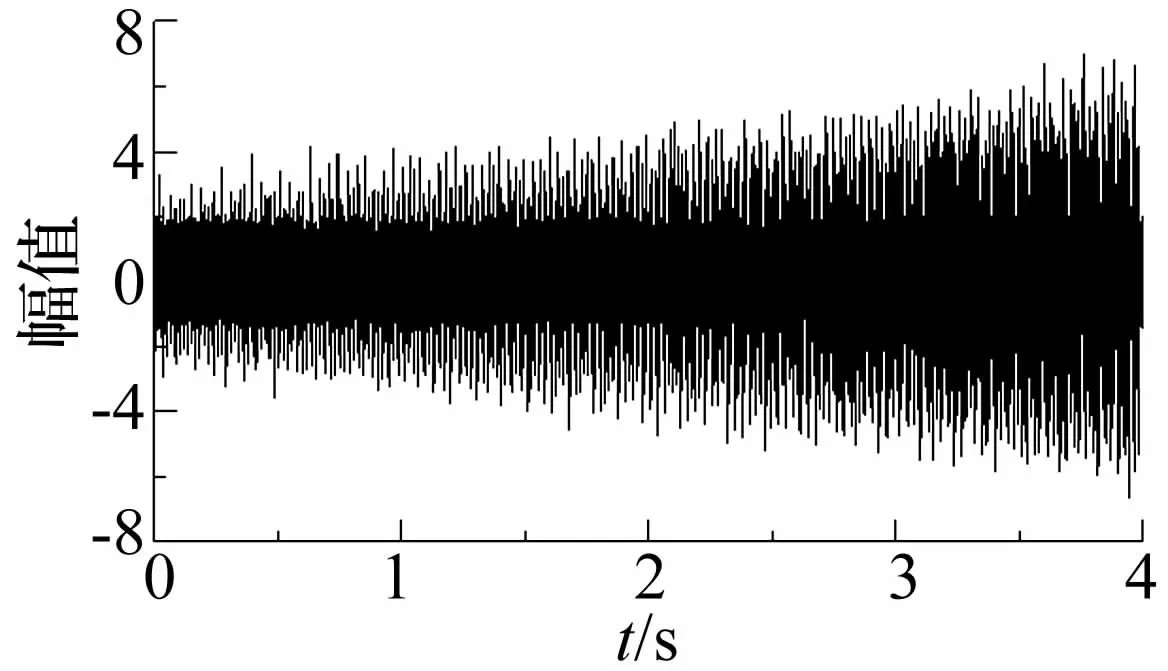
图2 仿真混合信号Fig.2 Simulated mixed signal
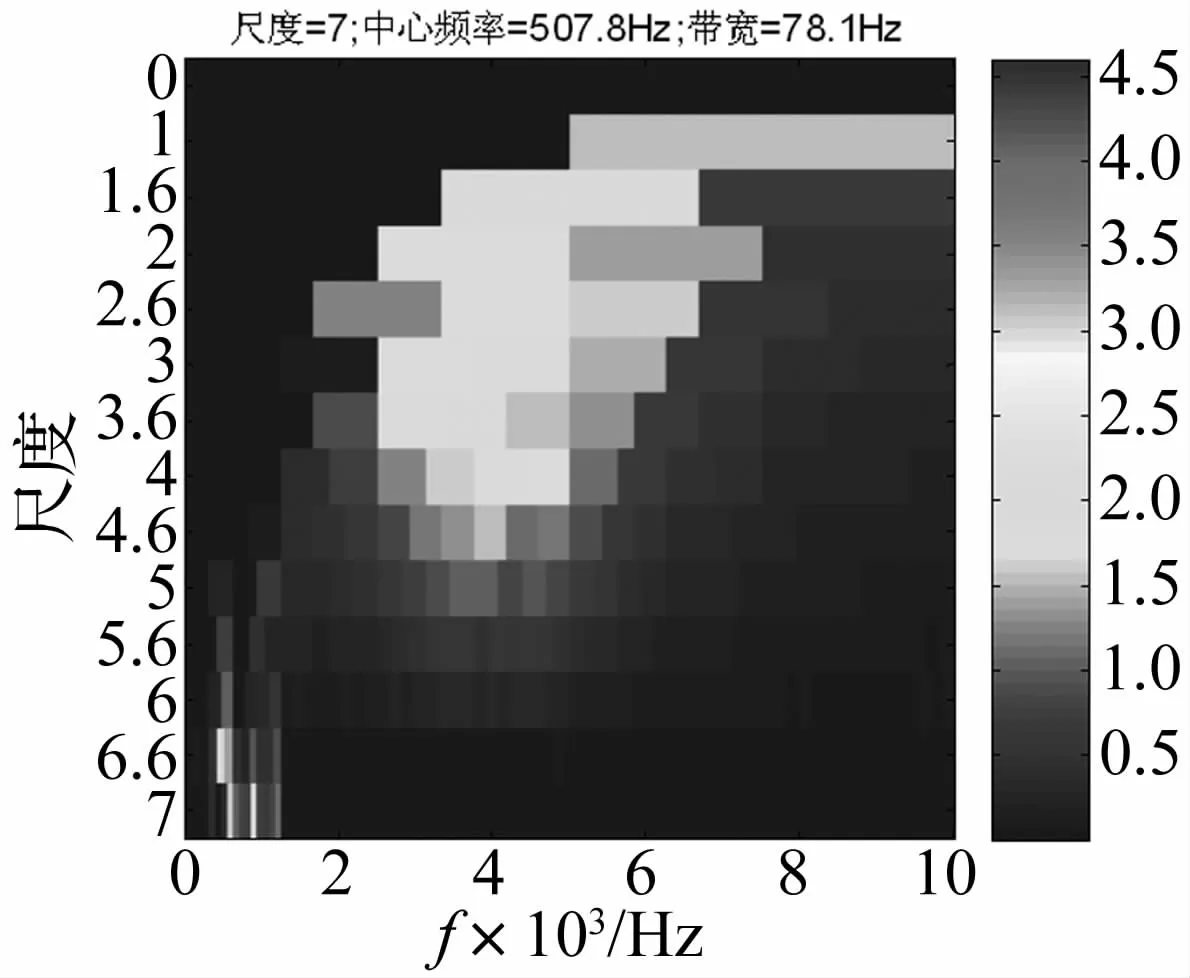
图3 仿真信号的Kurtogram图Fig3 Kurtogram of simulated signal
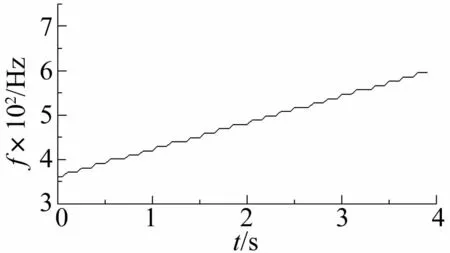
图4 仿真信号的峰值啮合倍频趋势线Fig.4 IDMH trend of simulated signal
然后,利用峰值搜索算法对IFCF趋势线进行提取。图7将提取得到的IFCF趋势线和设计的转频趋势线分别以上部方块图和下部细直线的形式在一张图中做对比。可以看出,两个变量同步变化,且比例基本保持不变。该图可以说明基于两次滤波结果的包络时频谱提取得到的IFCF趋势线具备代替轴承转频实现故障特诊角域重采样的资格。
最后,根据提取得到的IFCF趋势线,利用基于采样频率重调的重采样算法对两次滤波结果进行重采样。并利用傅里叶变换求出其对应的故障特征阶比谱(图8)。在故障特征阶比谱中,可以在1节故障特征阶比及其倍频上可以找到清晰的随阶比数衰减的峰值。因此,可以判断被监测轴承存在故障。

图5 自适应滤波后信号的Kurtogram图Fig5 Kurtogram of adaptive filtered signal
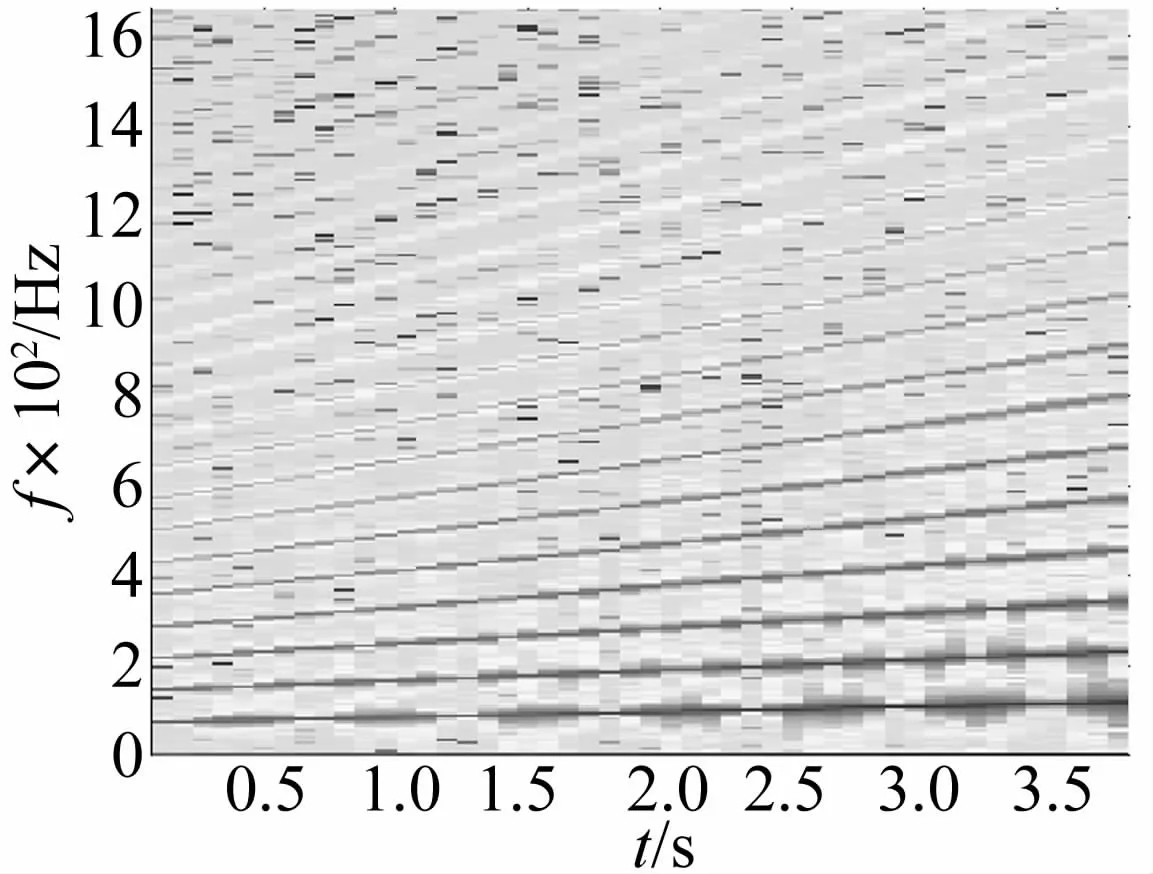
图6 包络时频谱图Fig.6 Envelope time-frequency representation
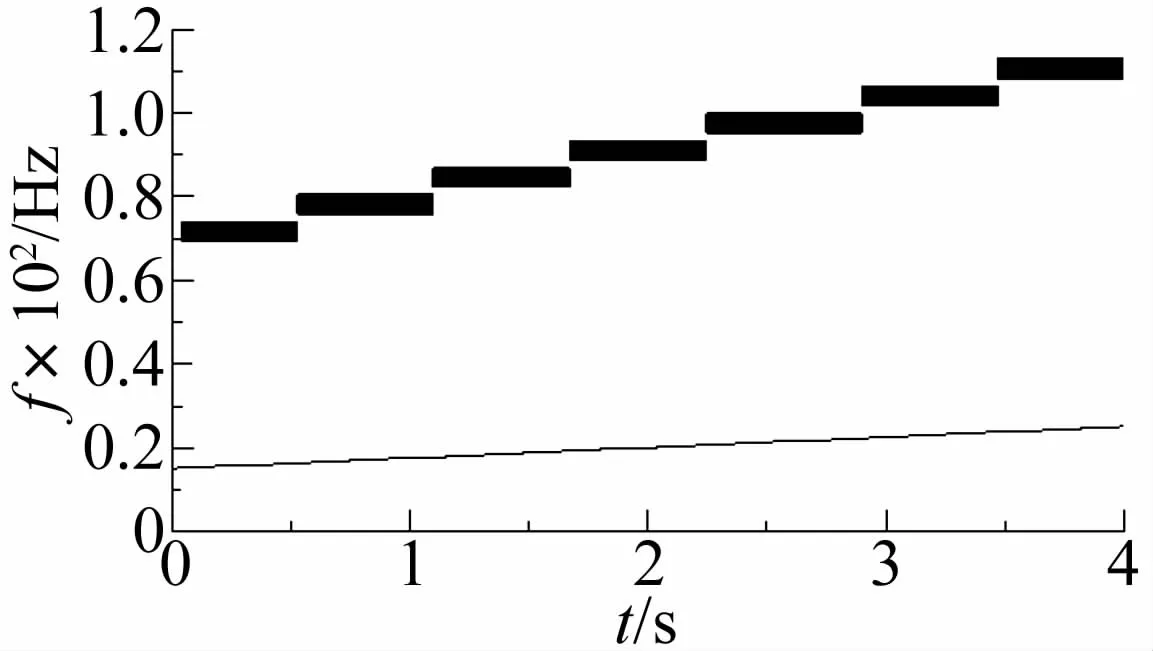
图7 IFCF趋势线与设计转频趋势Fig.7 IFCF trend Vs designed rotational frequency trend
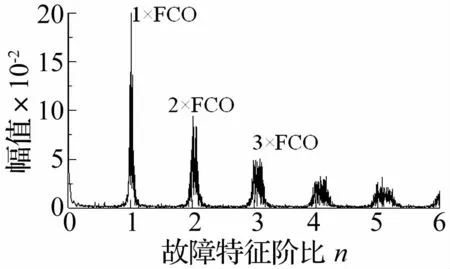
图8 故障特征阶比谱Fig.8 Fault characteristic order spectrum
根据以上介绍,可以证明本文提出的算法能够克服变转速和齿轮干扰的双重干扰,对处于弱势地位的故障轴承的运行状态做出的正确的判断。
3 实测信号分析
本文利用渥太华大学机械系的SpectraQuest机械故障试验台(如图9)模拟实际工况。具体将传感器布置在离齿轮较近的位置以保证齿轮振动的幅值优势。轴承转轴与齿轮箱输入轴同步转动,转速比为2.6∶1;滚动轴承的故障特征阶比为3.58;齿轮输入轴齿数Z为18;齿轮的啮合频率为6.92fs(fs为轴承转频)。

图9 试验台布局Fig.9 Set-up of the test rig
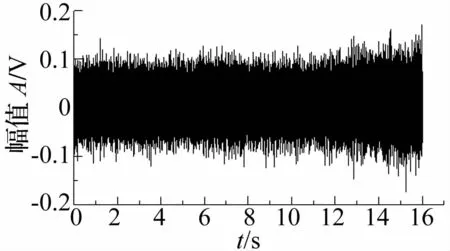
图10 实测混合信号Fig.10 Testmixed signal

图11 实测混合信号的时频谱Fig.11 TFR of themixed signal
图9与图10分别为实测混合信号的原始波形和时频表达。从图10中能清晰地找出与IDMH趋势线对应的时频分量,图13为从时频分析结果中提取出的IDMH趋势线。以该趋势线为基础构造参考传感器能够进一步实现对变转速齿轮噪源的去除。图12与图14分别为自适应滤波前后对应信号的kurtogram图。从两图的对比可以看出,改进的ANC滤波算法能够消除实际信号中齿轮噪源对提取轴承故障共振区的影响。
图15为两次滤波所得结果的包络时频包络谱。该时频图中包含着清晰的IFCF趋势。图16则将提取得到的IFCF趋势线与利用转速计测到的实际转速作对比:两者之间不但基本同步而且在每个时刻的比例几乎相等。图17为基于IFCF趋势线,利用采样频率重调算法得到的故障阶比域重采样信号的故障特征阶比谱。在故障特征阶比谱中,依然能在一阶比及其低阶倍频上找到明显的峰值。这证明了被监测轴承存在故障。
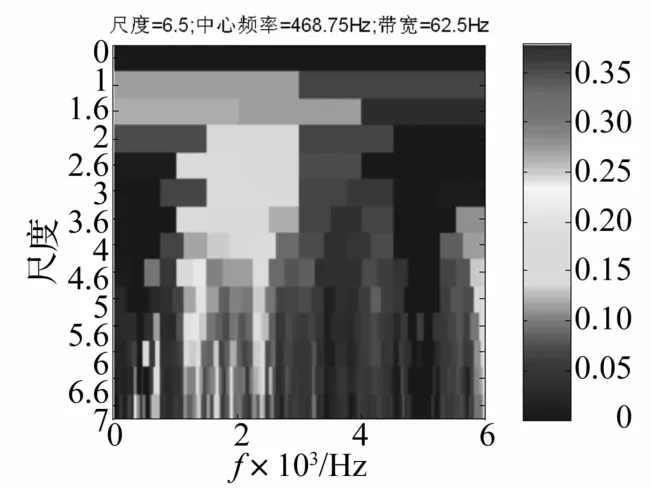
图12 实测混合信号的Kurtogram图Fig.12 Kurtogram of testmix signal
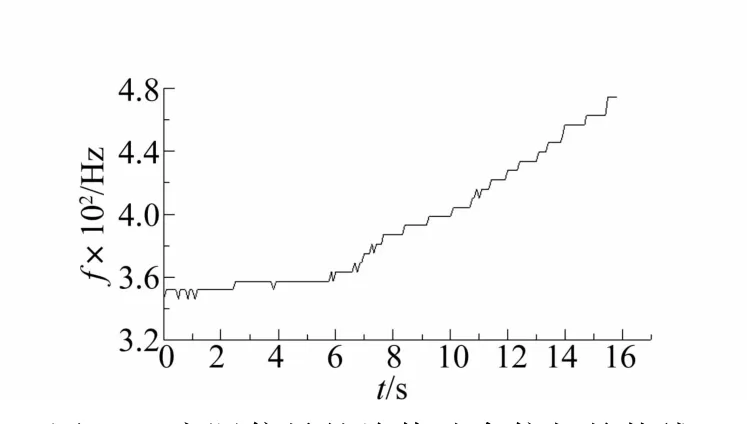
图13 实际信号的峰值啮合倍频趋势线Fig.13 IDMH trend of test signal
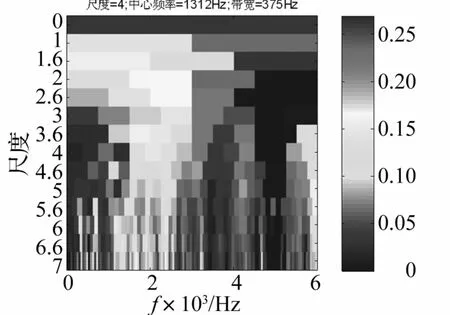
图14 自适应滤波后信号的Kurtogram图Fig.14 Kurtogram of adaptive filtered signal
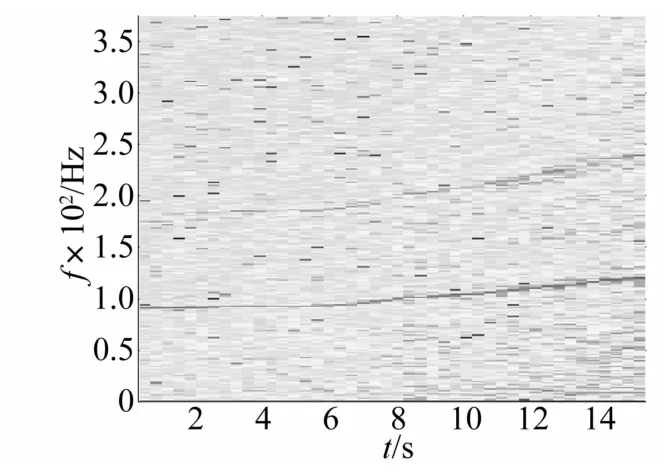
图15 包络时频谱图Fig.15 Envelope time-frequency representation
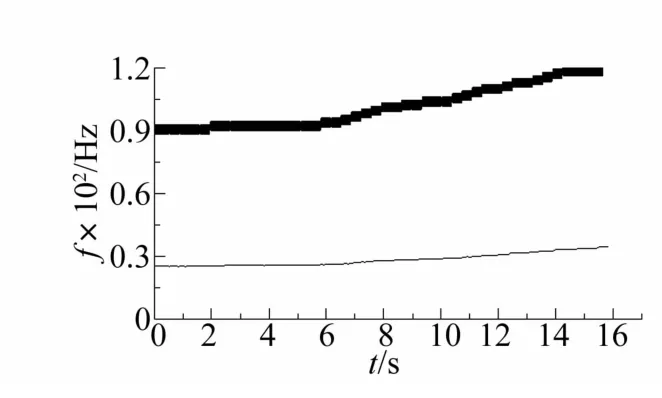
图16 IFCF趋势线与实测转频Fig.16 IFCF trend Vsmeasured rotational frequency
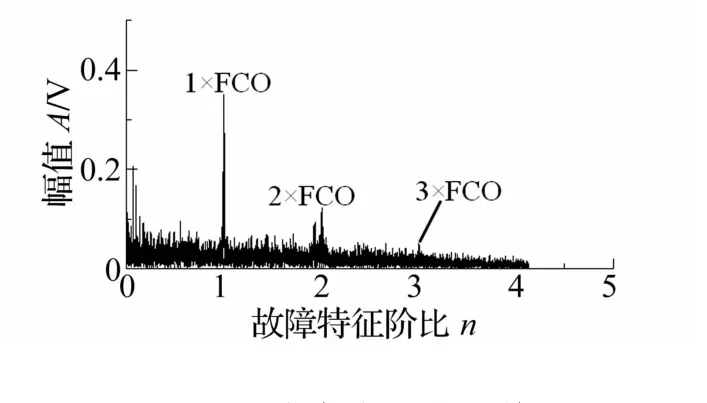
图17 故障特征阶比谱Fig.17 Fault characteristic order spectrum
4 结 论
本文提出改进的ANC的齿轮噪源削弱算法与基于FCO谱的轴承运行状态判别算法实现了在不使用任何辅助设备的前提下,在变转速和齿轮噪源的双重干扰下对滚动轴承的运行状态进行判断。
(1)利用IDMH趋势线构造的参考信号改进ANC算法,能够在不损害轴承部分的前提下对齿轮噪源进行削弱,使得能够对故障引起的共振频带进行直接提取。
(2)改进的ANC算法能够实现不依靠转速计和参考传感器的帮助完成齿轮噪源的削弱;
(3)联合应用基于谱峭度的滤波算法与STFT获取的包络时频图能够提取得到轴承的等效转频:IFCF趋势线;
(4)IFCF趋势线能够代替转频对变转速信号进行重采样,重采样信号的故障特征阶比谱能够用于判断滚动轴承的运行状态。
致谢:感谢国家自然基金项目(51275030)及加拿大渥太华大学机械工程系在资金及实验设备上的帮助。
[1]Randall R B,Antoni J.Rolling element bearing diagnostics-A tutorial[J].Mechanical systems and signal processing,2011,25(2):485-520.
[2]Antoni J,Randall R B.Unsupervised noise cancellation for vibration signals: part II—a novel frequency-domain algorithm[J].Mechanical Systems and Signal Processing,2004,18(1):103-117.
[3]Antoni J,Randall R B.Unsupervised noise cancellation for vibration signals:part I—evaluation of adaptive algorithms[J].Mechanical Systems and Signal Processing,2004,18(1):89-101.
[4]Fyfe K R,Munck ED S.Analysis of computed order tracking[J].Mechanical systems and signal processing,1997,11(2):187-205.
[5]赵晓平,张令弥,郭勤涛.旋转机械阶比跟踪技术研究进展综述[J].地震工程与工程振动,2008,28(6):213-219.ZHAO Xiao-ping,ZHANG Ling-mi,GUOQin-tao.Advances and trends in rotational machine order tracking methodology[J].Journal of Earthquake Engineering and Engineering Vibration,2008,28(6):213-219.
[6]Borghesani P,RicciR,Chatterton S,etal.A new procedure for using envelope analysis for rolling element bearing diagnostics in variable operating conditions[J].Mechanical Systems and Signal Processing,2013,38(1):23-35.
[7]Wang R Y.Bearing fault detection and oil debrismonitoring by adaptive noise cancellation[D].Ottawa:University of Ottawa,2008.
[8]Antoni J. The spectral kurtosis: a useful tool for characterising non-stationary signals[J].Mechanical Systems and Signal Processing,2006,20(2):282-307.
[9]Antoni J.Fast computation of the kurtogram for the detection of transient faults[J].Mechanical Systems and Signal Processing,2007,21(1):108-124.
[10]Liang M,Soltani Bozchalooi I.An energy operator approach to joint application of amplitude and frequency-demodulations for bearing fault detection[J].Mechanical Systems and Signal Processing,2010,24(5):1473-1494.

