基于拉普拉斯特征映射的旋转机械故障识别
李月仙,韩振南,黄宏臣,宁少慧
(太原理工大学 机械工程学院,太原 030024)
旋转机械是工业部门中应用最广泛的机械设备,齿轮-轴承系统作为旋转机械的核心部件在工业中发挥着无可替代的作用。目前的机械设备朝着大型化、复杂化发展,旋转部分复杂的运行工况容易出现各种不同形式的故障而影响正常工作,甚至会发生毁机事故,造成重大的经济损失。旋转机械常见的故障包括三类:一是滚动轴承故障,包括轴承内圈、外圈、滚动体及保持架故障;二是转子本体故障,包括不平衡、不对中、转子裂纹及支承松动等;三是齿轮故障,包括断齿、齿面磨损和齿根部裂纹等[1]。
对于复杂结构和系统的旋转机械在出现故障时所监测到的振动信号具有明显的非线性和非平稳特性,使用传统时频方法难以从复杂信号中提取出有效特征量。为了及时、准确地识别和诊断出故障状态,从监测信号中提取出有效信息量就尤为重要。常用的方法就是采用多个相关传感器和提取多个特征量以提高诊断精度,但是大量的冗余信息给故障分类带来了更大的复杂度。因此,消除信息冗余,提取出有效的故障分类特征量是我们一直所追求的目标之一[2]。
1 核方法
核方法是20世纪60年代由Minsky和Papert等人针对线性特征提取方法对于非线性信号进行特征提取时的局限性,无法解决现实世界中很多复杂的非线性问题而提出的一种非线性学习方法。通过引入核函数,将数据映射到高维空间中,在特征空间中展开学习,发现其存在的线性关系,实现了非线性问题的高效求解,同时避免了复杂的非线性映射的求解。
核主元分析法KPCA是最典型的非线性核方法,在高维特征空间中不涉及非线性优化,仅仅利用线性代数求解特征值问题,且由于KPCA使用了核函数,对非线性问题具有了较广的适用性,在机械过程检测和故障诊断领域已经得到了广泛应用和研究[3-5],但核方法的缺点也是很明显的,在参数选取时是不需要预先给定的,且在使用核函数时是知道具体的特征空间,使得核方法缺乏物理直观性。并且核函数对于故障诊断中的类可分性测度影响很大,选择不当会导致类可分性测度很小,使得不同类别的样本点在特征空间中出现相互重叠覆盖。而近年来流形学习方法的发展给机械故障诊断提供了一种新的思路。
2 拉普拉斯特征映射(LE)
2.1 流形学习算法
流形学习是人们在21世纪信息时代面对海量的高维信息而发展起来的一种新型的非线性降维及数据挖掘的新方法。它能有效地对高维非线性数据进行降维,从高维非线性数据中找出隐藏在高维观测空间数据中的低维结构表示,揭示其内在流形分布。在2000年发表的三篇论文中开创性地提出局部特征映射LLE和等距映射ISOMAP两种算法后,迅速在各领域中进行研究,并陆续出现了多种经典方法[6-10],如:拉普拉斯特征映射算法LE和局部切空间排列算法LTSA。因为流形学习已经在一些领域取得了显著效果,近几年被故障诊断领域的研究者引入到设备工况特征的高维数据的非线性特征挖掘和降维中,并显示了良好的效果和前途[11-13]。
2.2 LE算法描述
LE算法假设数据点分布在光滑黎曼流形上,其主要思想是通过Laplace-Beltrami算子来构造相应空间嵌入目标函数,实现高维数据在低维空间的嵌入。LE算法降维的实质就是寻找到一个平均意义上保持数据点局部邻近信息,即在原来高维特征空间中是近邻的点在低维表示中也应该是近邻点。因此,LE算法的求解
步骤2:定义邻接权矩阵W,可选择热核方式或简单连接方式。热核法:如果Xi与Xj是邻接点,则有Wij,否则为 0,其中 t为热核的宽度,其取值与邻域K值相适应;简单法:可以避免热核法中参数t的选择问题,如果Xi与Xj近邻,则Wij为1,否则为0,在本文中将采用简单法确定权值和权值矩阵。
步骤3:构建拉普拉斯特征矩阵L=D-W,最小化特征映射误差相当于计算下式中的最小特征向量。
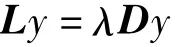
其中D为对角矩阵ij。L的最小d+1个特征值对应的特征向量u1,u2…ud就构成了低维嵌入结
由上所述,LE方法将降维和特征提取问题转化成对矩阵特征值和特征向量的求解,过程简单,不需要进行迭代计算,因此计算量和运算时间大大减少。
2.3 LE算法的聚类特性
根据LE算法的描述,LE算法是一种重点强调保持近邻关系的流形学习算法,可以有效地保持高维样本空间中具有相同或相近性质的近邻样本点“物以类聚”的聚类特性,因此,LE算法非常适用于机械故障不同样本分类识别问题。而对于LE算法,局部邻域的构建对低维流形提取效果至关重要,根据参考文献[14]在本文中将选用K=8的KNN法构建邻域图。转化为对图拉普拉斯算子的广义特征值求解问题[9]。根据图谱理论,如果数据均匀采样自高维空间中的低维流形,流形上的拉式算子可以由图上的Laplacian逼近,而图上的最前面的几个特征向量就是流形上L-B算子特征函数的离散逼近。LE算法可以描述为以下几步:
步骤1:构建邻接图G,可采用:近邻ε法或K近邻法,在本文中将选用K近邻域法(KNN);
3 构建高维特征空间
旋转机械状态识别与故障诊断过程是典型的模式识别的过程,特征提取是基础,识别方法是核心[3]。由于对旋转机械所监测到的振动信号复杂,包含着大量的冗余信息量,很难直接利用振动信号数据来评估。通过特征提取和转换技术把原始信号构建到特征空间,利用特定方法提取出能准确描述设备运行状态的信息。对振动信号进行时域、频域以及时频域特征量分析已被广泛使用,但是由于提取的不同特征参数对设备健康状态的规律性、敏感性和聚类性各不相同且表征规律不一,很难用某一个或几个特征参数来准确表征滚动轴承的运行状态。如何提取出规律性强、敏感性好的状态特征参数一直是故障诊断领域所追求的,也是研究的热点和难点之一。
为了提高运行状态和故障的识别准确率,本文将从多个角度尽可能地进行全方面分析。根据旋转机械在不同故障状态下不同特征参数的敏感性不同,构建如表1所示的26个特征量,其中Ei为采用db4小波包函数进行3层正交小波包分解得到均匀划分的8个子频带的滤波信号,将得到的8个子频带信号能量与总频率的相对能量比作为频域统计特征参数[11]。本文以上述26个特征参数作为训练样本,采用降维方法对高维特征数据进行学习,提取特征量。
E3i表示第 i+1个频带重构信号的能量,Ei=E3i/E表示第i个频带占总能量比,其中 i=0,1,…,7,E=表示总能量。
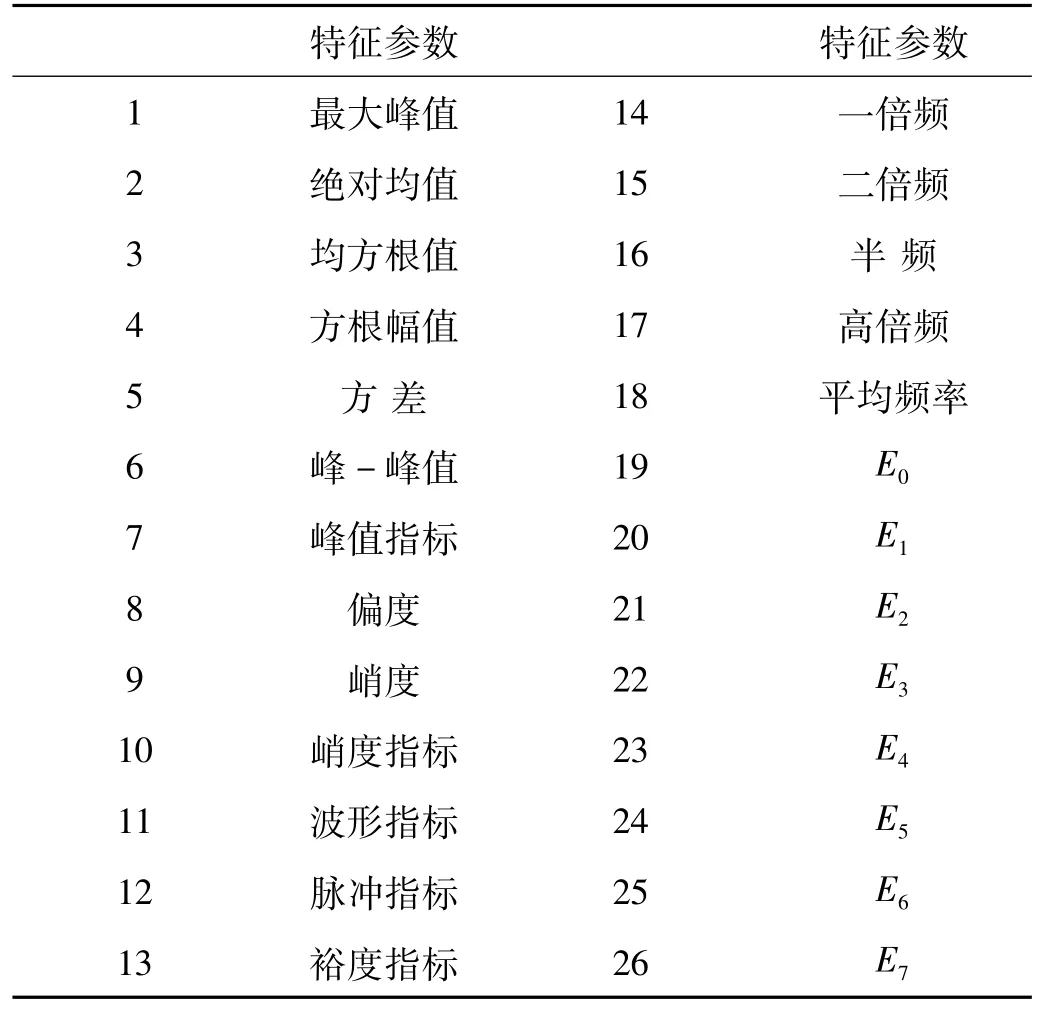
表1 特征参数表Tab.1 Characteristic param eter
4 典型故障类型实验
4.1 滚动轴承故障实验验证
滚动轴承实验中所采用的数据均来自美国凯斯西储大学电气实验室使用SKF6205-2RS滚动轴承所进行的实验[15]。所有实验数据是在选择下列实验条件下所测得的数据:电机负载为2 hp,转速为1 750 r/min,采样频率为48 kHz,其传感器位置为驱动端的轴承座上垂直位置。在本实验中,轴承内圈、外圈和滚动体上人为制造出滚动轴承三类典型故障类型,选用其故障尺寸为直径0.53 mm、深度0.28 mm所测数据作为实验依据。四种故障样本类型,每种故障选50组样本,每组样本26个维度,构建出N×m=(4×50)×26的特征矩阵。根据参考文献[16-17]所述,确定目标维数dim为选取的故障样本类型数减一,即dim=3。
从图1和表2中可知,图1(a)为PCA方法所得到的结果。从图中可以看出只有无故障样本可以准确识别,并且具有很好的聚类性,其他三种故障类型样本之间出现了相互交叉混叠,尤其是外圈故障样本分布散乱且识别率最低。可见PCA对滚动轴承故障样本的识别率和聚类效果不太理想。
图1(b)为KPCA提取的前三个主元K1K3的三维图。因为KPCA采用了参数σ=0.5的高斯核函数,所以从图中可以看出四种故障样本基本区分开来,各类故障样本实现了很好的识别和聚集,较PCA在样本的平均识别率和聚类性均有了较大的提高。但是,仍出现了不少的样本处于偏离位置,聚集性仍有待提高。
图1(c)为采用流形学习中的LE算法对高维特征空间进行特征融合提取的结果。滚动轴承的四种样本在三维空间中都呈现出很好的聚类性,且类与类之间明显地分离。与PCA和KPCA两种方法相比,LE方法能对高维样本空间提取出不同故障状态下的有效信息,从而实现了对滚动轴承故障状态的有效识别。

图1 滚动轴承故障分类识别Fig.1 Different fault classification of Rolling Bearing
4.2 转子故障实验
转子故障是旋转机械中常见的一类故障,在本节中,通过典型故障的分析找出故障的振动特征是进行模式识别的必要条件,是进行精密诊断的基础。
第一种,转子不平衡,是一种常见的故障类型,旋转机械中由于不平衡而失效约占30%;第二种,各转子轴线之间产生平行、轴线角度或综合位移等对中变化误差,即转子不对中。转子系统中约60%故障是由不对中引起的,是旋转机械转子系统中最常见的故障;第三种是转子弯曲,转子弯曲又分为中间弯曲和端部弯曲两种,在运行时会产生与质量偏心类似的旋转矢量激振力,同时在轴向发生与角频率相等的振动。第四种是基座或装配松动,基座和装配松动常和转子不平衡相伴生,表现出强烈的垂直方向振动[1]。
本节中四种典型转子故障均为某公司实验平台上所进行的模拟实验,选用电机转速均为2 976 r/min(fr=49.6 Hz)。同理,构建出如滚动轴承故障实验类似的N×m=(4×50)×26高维特征矩阵。分别采用PCA、KPCA和LE方法进行特征提取,降维结果如图2所示。
由于四种故障在时域和频域特征量中差别比较明显,故PCA方法对于四种故障也能基本识别,但每种故障的聚类性很差,且各种故障相互间的间隔不明显;KPCA比PCA在类内距有所提高外,样本识别率并没有明显提高,出现一定量的交叉混叠;而LE方法很明显地把类与类分离,虽然也存在错误识别,但相较PCA和KPCA,在高维空间中对状态样本的低维嵌入聚类提取敏感特征效果明显提高。
4.3 齿轮故障识别
本文齿轮故障识别实验数据,是在太原理工大学齿轮研究所振动及故障模拟实验平台上所测得,并选用轴承座垂直方向振动加速度信号作为诊断依据。实验采用的是材料为45#钢的单级渐开线直齿圆柱齿轮,大齿轮齿数为45,小齿轮齿数为30,压力角α0=20°,模数m=4,转速均为N=800 r/min,负载为400 N·m,采样频率为10 kHz。实验选用三个相同的小齿轮,一个为无故障齿轮,一个制造成齿面剥落,而另一个在某个齿根处切割长为5 mm的裂纹,作为齿轮的三种典型状态。同理,分别采集三种状态的振动信号,提取特征量构建N×m=(3×50)×26的高维矩阵进行降维和特征提取。由于在本齿轮实验中只选择三种类型,所以,目标维数dim=2的二维图像表示分类结果如图3所示。

图2 转子故障分类识别Fig.2 Different fault classification of Rotors
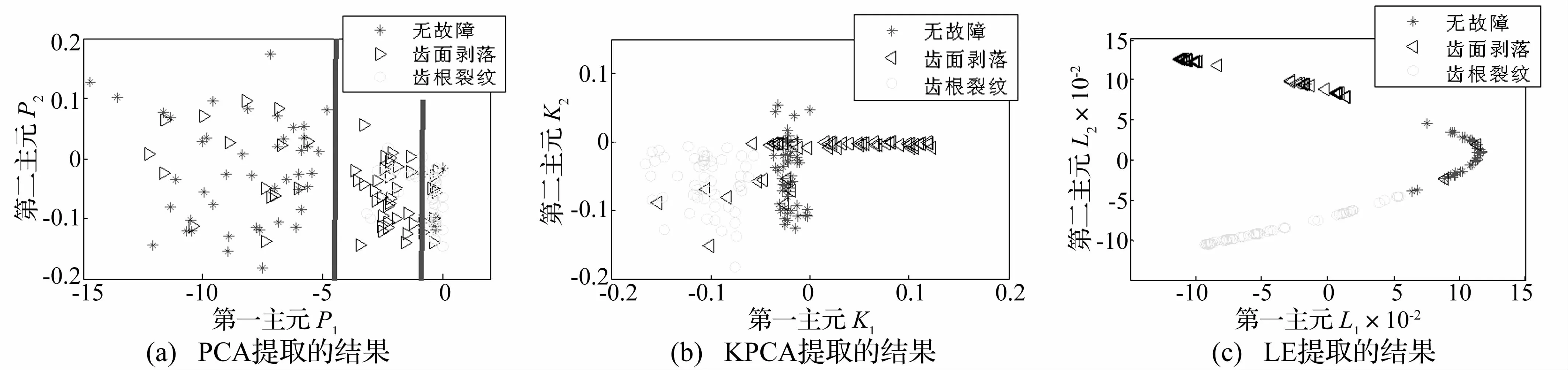
图3 齿轮故障类型识别Fig.3 Different fault classification of Gear1
从图3可以得出以下结论:图3(a)PCA对于识别分类效果不理想,出现了一些故障信号被识别成无故障类别,无故障信号被识别成故障类别,但基本能区分出故障和无故障,而对于齿面剥落和齿根裂纹两种故障不能很明显区分开,混在一起,且无故障的分布非常散乱;KPCA对于三种状态的识别比PCA在识别率和类内距都有了较好的提高,但是仍出现了一些错误识别现象,各种类别聚集性有了明显提高,但仍有待提高;而LE算法对于三种类别基本实现了较好的识别和区分,无故障类别的50组信号全部识别出来,几乎聚集在了一个点,对于齿面剥落和齿根裂纹故障信号也基本实现了识别,聚集在一起,但也出现了不少识别错误,一部分齿面剥落被识别出成无故障,一部分齿根裂纹被错误识别为齿面剥落。总体来说对于齿轮故障分类识别LE算法比PCA和KPCA在识别率、类内距Sb和类间距Sw都更具有优越性,详细数据见图4和表2。
5 实验评价指标
在模式识别中所选取的特征评价准则直接或间接反映出样本的分类效果,本文采用故障样本平均识别准确率、聚类分析法中的类间距Sb和类内距Sw来衡量提取特征的聚类效果[16-18]。类间距Sb用来描述不同类别分开的距离,类内距Sw表明每个类样本分布紧凑性。假定特征向量为{f1、f2、…、fdim},特征向量的目标维数dim。Sb和Sw两个参数的描述如下:
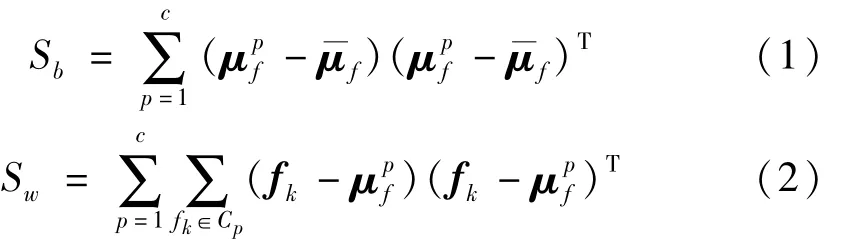
其中是每一类中 Cp(p=1,2,…c)样本特征向量的平均值是所有类型中特征向量的平均值。类间距Sb是用来描述类与类之间的距离,而类内距Sw则是用来描述每一类样本聚集程度的好坏,取值越小越好,而Sb/Sw可作为分类能力的主要指标。本文通过类内距和类间距分类指标的邻域选择策略,保证同类样本点的关联性,从而获得较好的聚类质量。通过三种方法,计算两组实验的Sb和Sw,结果见表2。
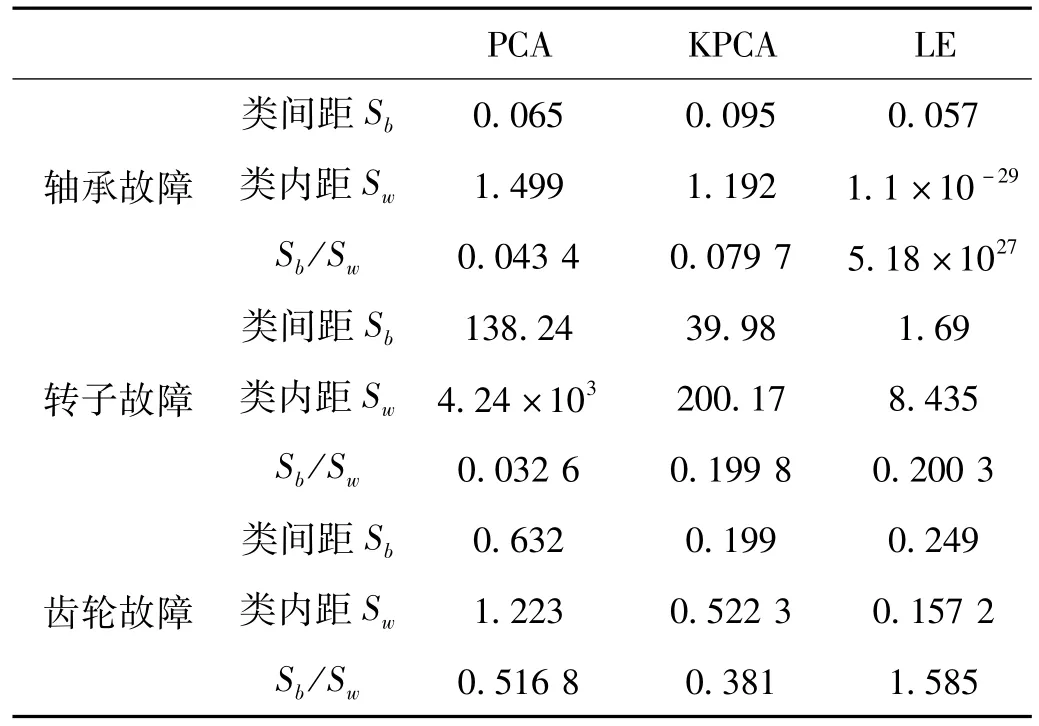
表2 特征参数值Tab.2 Characteristic parameters value
由表2和图4可知:LE方法的识别效果明显好于PCA和KPCA方法。PCA的效果最差,KPCA由于采用了高斯核函数,所以比PCA有了很大提高;在聚类性方面,尤其是类内距Sw,LE的效果最好,较前两种都有明显提高,在滚动轴承故障识别中,类内距Sw几乎为零,远远小于其他两种方法的结果,而Sb/Sw的比值,LE的比值也是最大,说明LE方法对特征提取降维效果最好。综上所述:LE方法相对PCA和KPCA在故障样本分类和识别中具有优越性。

图4 三种提取方法的识别率Fig.4 The recognition rate of threemethods
6 结 论
本文在拉普拉斯特征映射算法基础上,首次提出一种基于LE算法的旋转机械故障识别新模式。通过对旋转机械三类典型故障:滚动轴承故障、转子故障以及齿轮故障进行模拟实验验证。从模式聚类识别的角度进行分析,使用样本平均识别率、样本聚类性的类内距和类间距三个参数作为评价指标,三组模拟实验结果表明:LE算法相较于传统的PCA和非线性核方法KPCA,在由多特征量构建的高维特征空间中能够提取出更敏感、更准确地表征设备运行状态的特征量,提高了不同故障样本的分类识别性能,从而实现了旋转机械的故障诊断。
[1]廖伯瑜.机械故障诊断基础[M].北京:冶金工业出版社,2003.
[2]钟秉林,黄仁.机械故障诊断学(第三版)[M].北京:机械工业出版社,2007.
[3]蒋玲莉.基于核方法的旋转机械故障诊断技术与模式分析方法研究[D].长沙:中南大学,2010.
[4]李巍华,廖广兰,史铁林.核函数主元分析及其在齿轮故障诊断中的应用[J].机械工程学报,2003,39(8):65-70.LIWei-hua,LIAO Guang-lan,SHI Tie-lin.Kernel principal component analysis and its applcation in gear fault diagnosis[J].Chinese Journal of Mechanical Engineering.2003,39(8):65-70.
[5]邓晓刚,田学民.一种基于KPCA的非线性故障诊断方法[J].山东大学学报(工学版),2005,35(3):103-106.DENG Xiao-gang,TIAN Xue-min.Nonlinear process fault diagnosismethod using kernel principal component analysis[J].Journal of Shandong University(Engineering Science),2005,35(3):103-106.
[6]Seung H S,Lee D D.Themanifold ways of perception[J].Science,2000,290(5500):2268-2269.
[7]Roweis ST,Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(5500):2323-2326.
[8]Tenenbaum J,Silva D,Langford J.A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290(5500):2319-2323.
[9]Belkin M,Niyogi P.Laplacian Eigenmaps for dimensionality reduction and data representation[J].Neural Computation,2003,15(6):1373-1396.
[10]ZHANG Zhen-yue,ZHA Hong-yuan.Principalmanifolds and nonlinear dimensionality reduction via tangent space alignment[J].Journal of Shanghai University(English Edition),2004,8(4):406-424.
[11]栗茂林,王孙安,梁霖.利用非线性流形学习的轴承早期故障特征提取方法[J].西安交通大学学报,2010,44(5):45-49.LIMao-lin,WANG Sun-an,LIANG Lin.Feature extraction for incipient fault diagnosis of rolling bearings based on nonlinearmanifold learning[J].Journal of Xi’an Jiaotong University,2010,44(5):45-49.
[12]蒋全胜,李华荣,黄鹏.一种基于非线性流形学习的故障特征提取模型[J].振动与冲击,2012,31(23):132-136.JIANG Quan-sheng,LI Hua-rong,HUANG Peng.A fault feature extractionmodel based on nonlinearmanifold learning[J].Journal of Vibration and Shock,2012,31(23):132-136.
[13]黎敏,徐金梧,阳建宏,等.一种基于流形拓扑结构的轴承故障分类方法[J].控制工程,2009,16(3):358-362.LIMin,XU Jin-wu,YANG Jian-hong.et al.Classification method of bearing faults based on topological structure of manifold[J].Control Engineering of China,2009,16(3):358-362.
[14]王泽杰,胡浩民.流形学习算法中的参数选择问题研究[J].计算机应用与软件,2010,27(6):84-85.WANG Ze-jie,HU Hao-min.On parameter selection in manifold learning algorithm[J].Computer Applications and Software,2010,27(6):84-85.
[15] The Case Western Reserve University Bearing Data Center.http://csegroups.case.edu/bearingdatacenter/home.
[16]He Qing-bo.Vibration signal classification by wavelet packet energy flow manifold learning[J].Journal of Sound and Vibration,2013,332(7):1881-1894.
[17] He Qing-bo.Time-frequency manifold for nonlinear feature extraction in machinery fault diagnosis[J].Mechanical Systems and Signal Processing,2013,35(1-2):200-218.
[18]张学工.模式识别[M].北京:清华大学出版社,2010.146.

