两种传感器的位置优化及结构多种响应重构
张笑华,任伟新,方圣恩
(1.福州大学 土木工程学院,福州 350108;2.合肥工业大学 土木与水利工程学院,合肥 230000)
传感器系统在结构健康监测系统中扮演着重要的角色。传感器的分布和相应的信号质量会影响整个健康监测系统的功能。然而,由于经济上和现场安装的一些原因,安装在结构上的传感器数目有限。因此,如何有效的布置有限数目的传感器以期能获得尽可能多的信息已经引起了很多学者的兴趣,提出了大量的传感器位置优化布置的方法[1-7]。
Kammer等[2-3]提出有效独立法(Effective Inde-pendence,EfI)来优化布置传感器的位置。这种方法是基于每个候选传感器位置对于识别模态的线性独立性贡献多少来判定的。该方法需要事先确定好所需要的传感器数目。因此Kammer[8]扩展了该方法,在位置优化过程中同时确定传感器的数目以期保证信号达到一定的信噪比水平。Hemez等[9]进一步修正了EfI方法。该方法的基本思想是将传感器布置在具有较大模态应变能的自由度上。Heo等[10]提出了用模态动能优化传感器位置的方法。该方法布置传感器的准则是最大化测量位置的结构动能。Paradinitriou等[11]引入信息熵来优化布置传感器的位置。信息最丰富的测试数据是在参数估计中有最小不确定性的数据,即最小化信息熵的数据。因此该方法选择的传感器位置是能使得信息熵最小的位置。Meo等[12]提出的方差法(variance method,VM)基于最优信息子集技术利用测量点的模态来估计剩余其它测点的模态。
已有的传感器位置优化方法,要么是为了更精确的识别模态,要么是为了结构损伤识别。很少有文献涉及以重构结构响应为目标的多种传感器的位置优化。一个有效的结构监测系统需要全面的信息,包括结构的局部信息和全局信息。随着传感器技术的发展,传感器网络系统变得越来越复杂和多样化。传感器系统可以包括应变片,加速度计,位移计,无线传感器,光纤传感器,等等。尽管多样的传感器可以给结构提供更全面更精确的信息,但它们自身的特性和局限性使得同时优化它们的位置变得非常复杂。
考虑到位移是用于监测结构的全局整体性,应变是用于监测结构局部变化,并且位移和应变之间有个几何关系,本文提出了利用卡尔曼滤波算法以重构响应为目标的两种传感器数目确定和位置优化的方法。这两种传感器分别是应变传感器和位移传感器。与传统方法不同,本文提出的方法是同时优化这两种传感器的位置,并且在优化位置的测量信息被用来重构结构关键位置的响应。在优化位置的过程中,当响应重构误差达到某一标准时优化程序终止,由此确定了传感器的数目和位置。最后用二维桁架结构数值研究了提出方法的有效性和可行性。研究结果表明该方法可以同时优化位移传感器和应变传感器的位置,确定两种传感器的数目。利用在优化位置的测量信息重构的响应与数值计算的响应吻合良好。综合利用两种信息重构其它位置的响应精度要优于用单种信息重构得到的结果。
1 理论介绍
1.1 离散状态空间方程
结构的运动可以用下列离散的状态空间方程来表示[13]:
式中:zk,yk和uk分别表示在 kΔt时刻的离散状态向量,观测向量和外部激励向量;Δt是采样时间间隔;A和B分别表示离散的状态矩阵和离散的输入矩阵;C和D分别表示输出矩阵和直接传输矩阵;wk是过程噪声向量;vk是测量噪声向量;wk和vk均假设为零均值白噪声,方差矩阵分别为Q和R。如结构的二阶运动方程是用模态坐标表示的,即:
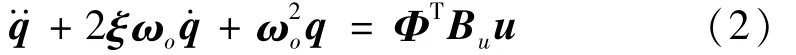
式中:q是模态坐标,Φ是位移模态振型矩阵,ξ是模态阻尼矩阵;ωo指模态频率矩阵;Bu是激励的位置矩阵。则(1)的状态空间方程中各项为:
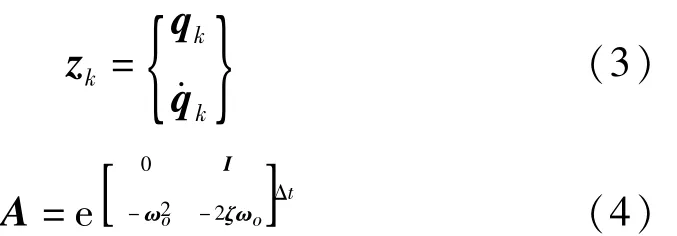
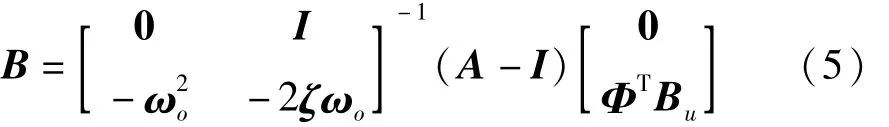
测量方程中y向量包括应变和位移响应,则

式中:Ψ=BΦ,B是位移-应变矩阵,与有限元单元的类型有关系。
1.2 卡尔曼滤波算法
卡尔曼滤波算法是以最小均方误差为估计的最佳准则来递推估算状态向量z^。卡尔曼滤波算法的操作包括预测和更新两个阶段,可用下列五个方程来表示[14]:

式中:Pk是后验估计误差方差矩阵;Kk是最优卡尔曼增益矩阵。
模态振型矩阵可以分成两部分:选择振型矩阵和截断振型矩阵。一般选择振型矩阵包含的是结构振型中对响应贡献较大的低阶振型。在实际使用中不需要用到所有的模态,一般仅考虑结构中低阶的前几阶模态即可,尤其是对于大型结构来说。因此,线性结构中包括所有感兴趣位置的应变响应和位移响应,可以表示为

式中,下标‘s’表示选择的模态;Ces表示所有感兴趣位置的选择模态振型矩阵组成的输入矩阵。测量位置的响应可以用相似的另外的式子来表示

式中,上标‘m’表示测量的;Cms表示测量位置的选择模态振型矩阵组成的输入矩阵。利用卡尔曼滤波算法和测量响应可以估计状态向量。由此结构的响应可以用下式重构得到

式中,上标‘e’表示重构。
重构响应的误差可以表示为重构响应时程序列与真实响应时程序列之间的差值
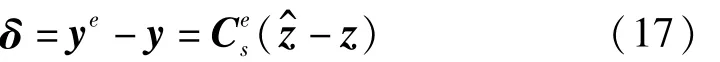
相对重构误差定义为重构误差δ与测量噪音标
1.3 优化目标方程
准差的比值
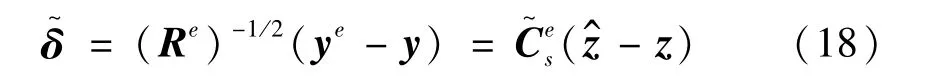
式中:Re是需重构响应的位置对应量的测量噪声方差组成的矩阵。
因此相对重构误差的方差可按式(19)计算

由于应变响应和位移响应的数量级不同,矩阵是病态的。在利用卡尔曼滤波算法估计状态向量过程中,病态的矩阵会影响卡尔曼增益矩阵的计算。可利用位移测量噪声和应变测量噪声的标准差来规则化位移模态振型矩阵和应变模态振型矩阵。由此可得到卡尔曼滤波算法增益矩阵的公式

式中:Rm是测量位置对应量的测量噪声方差组成的矩阵是规则化的测量位置的由选择模态振型矩阵组成的输出矩阵。
此可得到两种传感器位置优化的目标方程

约束方程
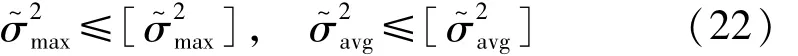
其中
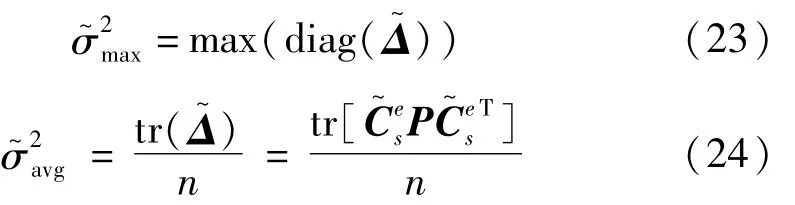
和分别表示规则化的最大重构误差方差和规x则化的平均重构误差方差。分别是规则化的最大重构误差方差和规则化的平均重构误差方差的阀值。
传感器位置优化的目标是尽可能准确的重构结构响应。当删除某候选传感器位置时,矩阵的秩达到最小,即平均重构误差达到最小,表明该候选传感器位置对响应重构的贡献小,可以不考虑为最终的传感器位置。在优化程序中,随着传感器数目的不断减少逐渐增大,当二者中的任何一个达到预设的阀值时,程序停止迭代,由此可确定应变传感器和位移传感器的数目。此时均可满足小于等于预设的阀值。当最终传感器位置和数目确定后,利用这些位置的测量响应和式(16)重构结构的响应。
2 传感器优化布置和数目确定及响应重构步骤
(1)从相应的有限元模型中提取结构振型,并决定要选取哪些振型;
(2)利用式(21)和(22)优化传感器的位置和决定传感器的数目;子步骤如下:
(2.1)用对应的传感器测量噪声的标准差规则化输出矩阵C;
(2.2)从候选的传感器位置中删除第i个位置,计算第i个平均规则化重构误差方差值;当删除某个位置后,规则化重构误差方差值最小,该位置从候选群中删除;剩下的候选位置组成新的一个传感器位置候选群;此时,计算最大规则化重构误差方差和平均规则化重构误差方差,并与相应的阀值比较,看是否已经达到阀值;
(2.3)如果此时最大规则化重构误差方差和平均规则化重构误差方差都仍旧小于预设的阀值,利用新的传感器位置候选群重复步骤2.2,直到最大规则化重构误差方差或者平均规则化重构误差方差等于或者大于预设的阀值,程序停止迭代。此时剩下的位置候选群就是两种传感器的数目和位置;
(3)利用Newmark法计算结构受外部激励下的位移响应和应变响应;给选择的位置上的响应加噪声并视之为测量响应;
(4)利用这些测量响应和式(16)重构结构关键位置的响应;
(5)把重构的响应和计算的响应进行对比,检测重构响应的精度。
3 数值算例
本文用二维桁架结构数值模拟了两种传感器位置优化和结构响应重构的过程。该桁架结构有25个单元,14个节点和28个自由度,如图1所示。应变传感器假设贴在单元上表面的中心位置以测量单元的应变。节点1,2,13和14不作为位移传感器位置的候选群。因此,共25个单元为应变传感器的位置候选群,节点3-12的10个y向自由度和10个x向自由度为位移传感器的候选位置,并且这些位置的响应也假设为需要重构响应的关键位置。该传感器位置优化方法是基于振型的,如果目标振型选定,优化的位置与外在激励无关。由于土木工程结构中随机激励比较常见,并且随机激励下的结构动力响应比起简谐激励或者自由振动下的响应包含更多的振动模态,因此本数值算例将用窄带随机激励作为示例。假设窄带随机激励y向加载于节点4。在这种加载工况中,x向位移很小,因此后面不对x向位移的重构结果进行分析讨论。
假设每种传感器的每个位置的测量噪音标准差相同并且是个常数,同时它们与信号的强度无关。本文假定应变传感器测量噪音标准差为σ=0.08 u,位移传感器测量噪音标准差为σd=0.001 5 mm。考虑了三种情况下的传感器布置工况:
工况1:用本文提出的方法优化布置位移传感器和应变传感器,并且重构位移和应变响应;
工况2:总传感器数目与工况一相同,用EfI方法布置位移传感器;
工况3:总传感器数目与工况一相同,用EfI方法布置应变传感器。
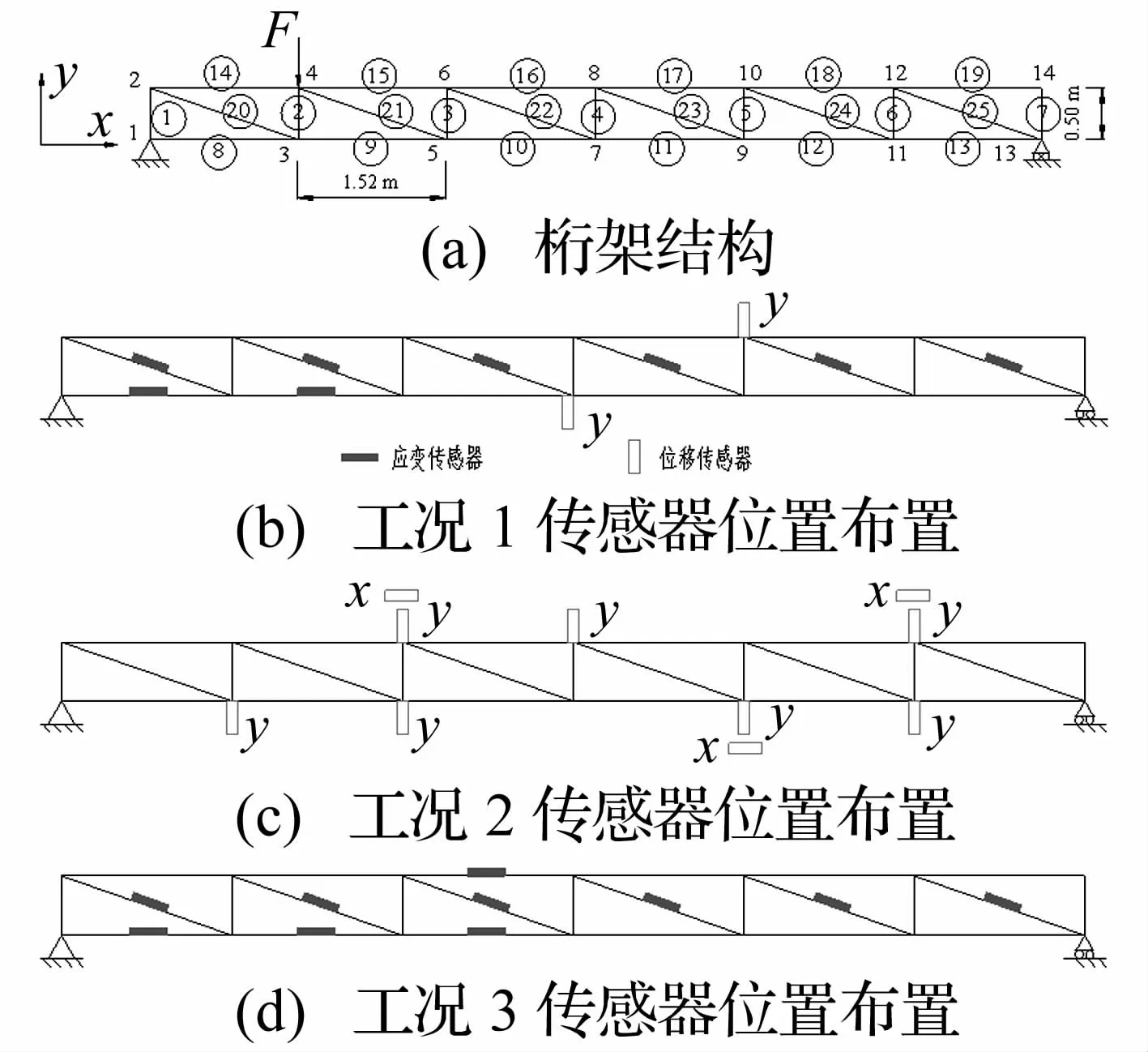
图1 桁架结构和各工况传感器位置布置图Fig.1 25-Bar truss structure and sensor locations
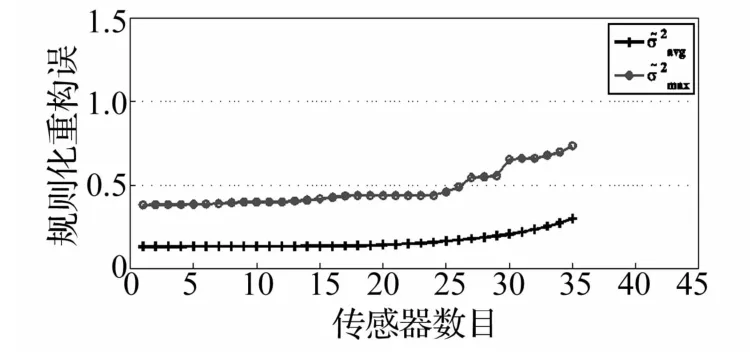
图2 重构误差随传感器数目变化的趋势Fig.2 Variation of theoretical reconstruction errorswith number of sensors
选取前6阶模态为目标模态。设置阀值如下。图 1(b)-(d)是各工况的传感器位置布置,总共有10个传感器。工况1是用本文提出的方法优化两种传感器的位置,优化结果是8个应变传感器和2个布置在y向的位移传感器。工况2是仅布置位移传感器,其中有7个传感器测量y向位移,3个传感器测量x向位移。
图2描绘了工况1平均规则化重构误差方差和最大规则化重构误差方差着传感器位置数目减少的变化趋势。随着传感器位置数目的减少而增大。当它们中的任何一者增大到预设的阀值时,优化程序停止迭代。由此得到在该约束条件下的传感器数目和优化的位置。
利用优化位置上的加噪声后的应变和位移响应,重构结构其他位置的响应。图3是工况1的单元1重构的应变时程和计算时程的对比和节点12重构的y向位移时程和计算时程的对比。从图3可以看到,重构的时程曲线与计算的时程曲线吻合非常良好。
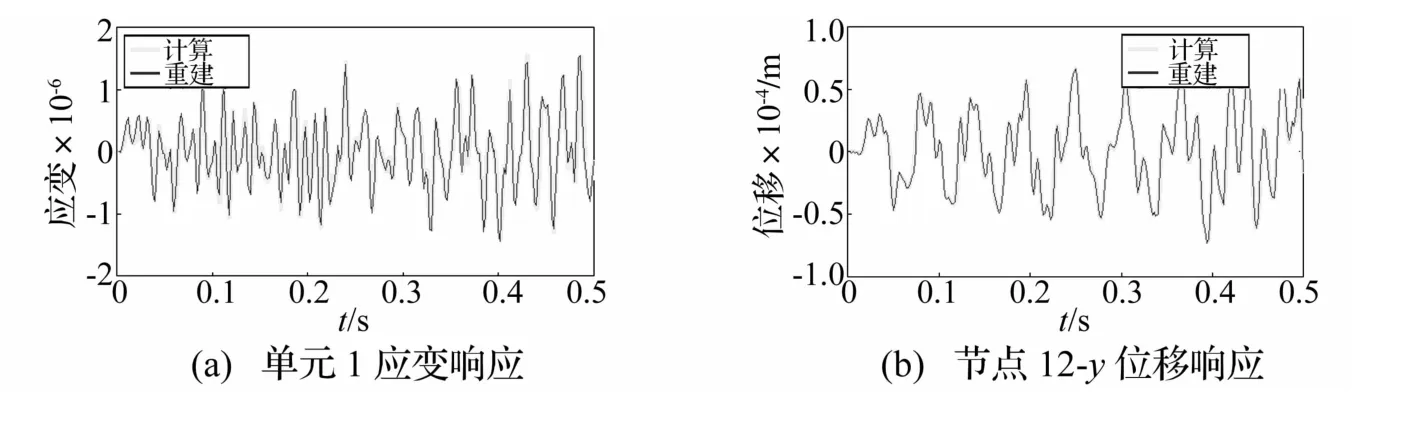
图3 重构和计算的时程响应对比(工况1)Fig.3 Comparison of reconstructed and real responses
重构时程响应的精度用相对百分比误差来衡量,定义如下

式中“std”指标准差。
图4(a)是工况1重构得到响应的相对百分比误差。不论是应变响应还是位移响应,重构得到的结果精度都高。对于应变重构响应的结果,大部分的百分比误差都在10%以下;而位移重构响应的百分比误差都在2%以下。单元2和19的应变重构结果较差,原因主要是:① 在该加载工况下,这些位置的应变响应比较小,信号的信噪比较差;② 这些位置的应变响应包含了更多的高频成分。
图4(b)是工况2的重构响应相对百分比误差。工况2是仅布置位移传感器,用测量位移响应重构关键位置的应变和位移响应。从图4(a)和图4(b)对比中可以看到,工况2得到的重构百分比误差要高于工况1得到的结果。工况3是仅布置应变传感器,用应变测量响应重构关键位置的位移和应变响应。对比图4(a)和图4(c),由于工况3布置的10个传感器均为应变传感器,因此工况3得到的应变重构结果精度略优于工况1得到的结果。但工况3得到的位移重构结果误差要大于工况1得到的结果。
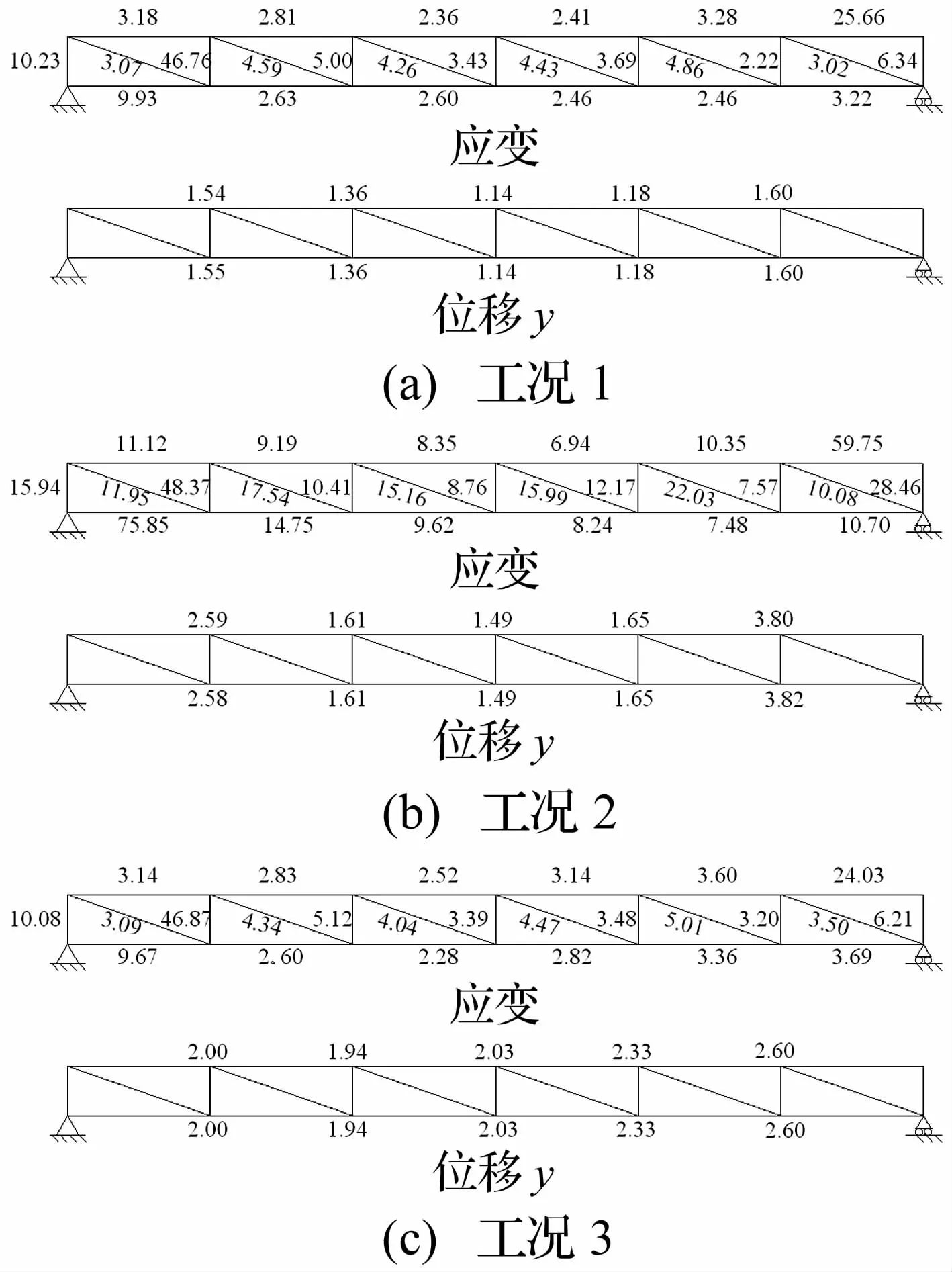
图4 相对百分比误差(%)Fig.4 Relative percentage errors(%)
4 结 论
本文提出了利用卡尔曼滤波算法以结构多种响应重构为目标的应变传感器和位移传感器位置优化及数目确定的方法。该方法有如下优点
(1)不同于传统方法,两种传感器的位置是同时优化;
(2)不需要预先设定传感器的数目,在优化程序中,通过响应重构误差达到预设的阀值来确定传感器数目;
(3)数值算例结果显示重构响应和计算响应时程吻合良好;
(4)数值算例结果表明综合利用两种测量响应重构结构响应的精度高于用单种响应重构得到的结果。
[1]Kammer D C. Sensor placement for on-orbit modal identification and correlation of large space structures[J].Journal of Guidance,Control and Dynamics,1991,14(2):251-259.
[2]Kammer D C,Yao L. Enhancement of on-orbit modal identification of large space structures through sensor placement[J].Journal of Sound and Vibration,1994,171(1):119-139.
[3]钱锋,王建国,汪权,等.基于模态应变能分布的压电致动器/传感器位置优化遗传算法[J].振动与冲击,2013,32(11):161-166.QIANFeng,WANG Jian-guo,WANG Quan,et al.Optimal placement of piezoelectric actuator/sensor using genetic algorithm based on modal strain energy distribution[J].Journal of Vibration and Shock,2013,32(11):161-166.
[4]谢强,薛松涛.结构健康监测传感器优化布置的混合算法[J].同济大学学报(自然科学版),2006,34(6):726-731.XIE Qiang,XUE Song-tao.A hybrid algorithm for optimal sensor placement of structural healthmonitoirng[J].Journal of Tongji University(Natural Science),2006,34(6):726-731.
[5]Shi Z Y,Law S S,Zhang L M.Optimum sensor placement for structure damage detection[J].Journal of Engineering Mechanics,2000,126(11):1173-1179.
[6]Guo H Y,Zhang L,Zhang L L,et al.Optimal placement of sensors for structural healthmonitoring using improved genetic algorithms[J].Smart Materials and Structure,2004,13(3):528-534.
[7]秦仙蓉,张令弥.一种基于QR分解的逐步累积法传感器配置 [J].振动、测试与诊断,2001,21(3):168-173.QIN Xian-rong, ZHANG Ling-mi. Successive sensor placement for modal paring based-on QR-factorization[J].Journal of Vibration,Measurement&Diagnosis,2001,21(3):168-173.
[8]Kammer D C.Effectof noise on sensor placement for on-orbit modal identification of large space structures[J].Journal of Dynamic Systems,Measurement,and Control,1992,114(3):436-443.
[9]Hemez F M,Farhat C.An energy based optimum sensor placement criterion and its application to structure damage detection[C]//Proceedings of the 12th International Conference on Modal Analysis,Society of Experimental Mechanics,Honolulu, Hawaii(1stedn.),1994,1568-1575.
[10]Heo G, Wang M L, Satpathi D. Optimal transducer placement for healthmonitoring of long span bridge[J].Soil Dynamics and Earthquake Engineering,1997,16(7-8):495-502.
[11]Papadimitriou C,Beck J L,Au S K.Entropy-based optimal sensor location for structuralmodel updating[J].Journal of Vibration and Control,2000,6(5):781-800.
[12]Meo M,Zumpano G,On the optimal sensor placement techniques for a bridge structure [J]. Engineering Structures,2005,27(10):1488-1497.
[13]Balageas D,Fritzen C P,Güemes A.Structural health monitoring[M].Newport Beach,CA:ISTE,London,2006.
[14]Welch G,Bishop G.An introduction to the Kalman filter[R]. Technical Report, University of North Carolina,Chapel Hill,NC,USA,2001.

