钢筋混凝土桥墩考虑地震反应与能力相互作用的抗震设计方法
郭 进,王君杰,董正方
(同济大学 土木工程防灾国家重点实验室,上海 200092)
基于性能的抗震设计理论是Bertero等[1-2]首先提出的。这种思想已广泛被接受,并得到日益深入的研究和应用,在实践中也已取得巨大的成功。基于性能的抗震设计要求较为准确地计算结构的地震反应,并对结构各构件的性能做出合理的评价。但是目前国内外规范[3-6]一般都将钢筋混凝土桥墩的地震反应计算和性能评估分开,其基本设计思想是D<C,即需求小于能力。这种不考虑地震反应与能力相互作用,强行将反应与能力独立开来的设计方法是不准确的,与钢筋混凝土的材料特性和基本的力学知识不符。导致这种不符原因有未考虑动轴力现象、未考虑双向弯曲现象、未考虑强度退化现象。针对这一问题,本文着重考虑损伤导致的强度退化现象。
钢筋混凝土桥墩是带损伤工作的,基于性能的抗震设计方法允许结构在较大地震作用下产生损伤。一般情况下,其能力(强度等)会随着损伤的发展而降低。强度退化程度与地震反应大小是相关的,在反应计算中,需要不断地根据反应确定强度退化的大小,即不断地对能力进行修正。能力的改变又会继续影响反应的大小,因此,能力与反应是相互耦合的。
从以上可以看出,为了准确地反映构件在地震作用时的特性,需要考虑损伤导致的强度退化,即考虑地震反应对构件能力的影响。本文将给出具体的考虑强度退化方法,提出钢筋混凝土桥墩考虑反应与能力相互作用的方法和设计流程,最后通过算例说明所提方法的可行性。
1 强度退化的考虑方法
可以采用两种方式考虑强度退化[7],它们均以再加载曲线指向峰值点的滞回模型为基础。第一种通过改变滞回模型的骨架曲线(图1(a)),第二种通过改变再加载指向点的承载力或变形来反映强度退化(图1(b))。图1中F是横向力,u是横向位移。图1(a)中是正向再指向点的屈服力,2)是负向向再指向点的屈服力。图1(b)中是正向力再加载指向点的位移增量,p是正向力的退化大小是负向力的退化大小。从现有研究文献来看,第一种方式应用较多,如Wang等[8]提出的强度退化模型便属于第一种方式。
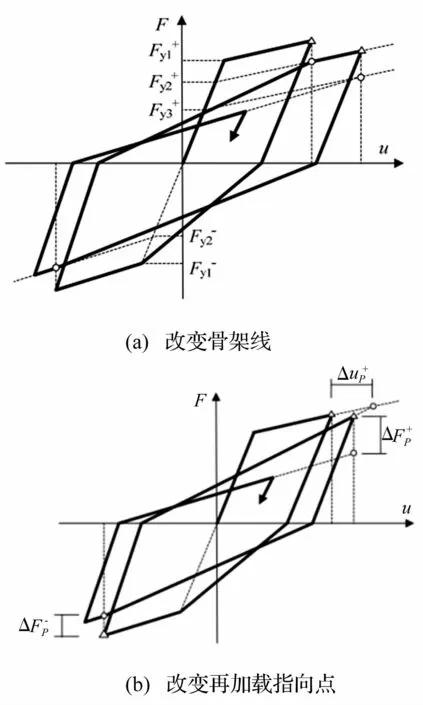
图1 指向峰值点的滞回模型的强度退化示意图Fig.1 Strength deterioration in peak oriented model
本文采用图1(a)所示的通过改变滞回模型的骨架曲线的方式考虑强度退化现象。
1.1 强度退化的一般数学表达式
钢筋混凝土强度退化的机理较为复杂,但一般可以认为钢筋混凝土的强度退化与其损伤紧密相关。所以从逻辑来讲,可以建立强度退化与损伤指标之间的关系。文献[9]中通过已有的强度退化模型,总结出了一般的改变骨架曲线的强度退化滞回模型(图1(a))的数学表达式:


式中,S为退化后的强度值,可以是力或弯矩等;S0为发生强度退化前的强度;f(D)为强度退化函数,与构件的特征有关。
损伤尚未发生时,不发生强度退化,即当D=0时,ΔS=0,代入式(2)可得

另外,退化后的强度不能超过初始强度,也不能为负值,即有0≤S≤S0,代入式(1)可得

式(4)是强度退化函数f(D)的边界条件。
从式(2)可以看出,确定强度退化本质上归结为确定强度退化函数f(D)。
1.2 强度退化模型的建立
目前广泛用于模拟钢筋混凝土的滞回模型有:双线型模型、Clough模型[10]、Takeda模型[11]等。以上 3种模型都没有考虑强度退化现象,其中双线型模型不能考虑刚度退化。Clough模型相对简单,本文以Clough模型为基础,通过改变滞回模型的骨架线来体现强度退化,如图2所示,M为弯矩,θ为转角,k1、k2分别是初始刚度和强化刚度。图 2中,Myi(i=1,2,3,4)是考虑强度退化后的屈服弯矩。My为屈服弯矩。

图2 考虑强度退化的Clough滞回模型Fig.2 Cloughmodel considering strength degradation
滞回模型的滞回规则为:① 首次加载时按骨架曲线前进;② 任何时候的卸载刚度与屈服前加载刚度相同;③ 在卸载阶段再加载时,将沿着卸载线加载,直至卸载开始点,如图2中,当从点13加载至点14后卸载至点15,再加载路径为15→14→16;④ 反向加载指向点为所指方向的最大位移点。如图2中,由点9反向加载时,指向最大位移点10,点10与点5的曲率相同,是点5考虑强度退化后的点。但是有一个例外,当所指方向尚未屈服时,则指向屈服点。如图2中3→4,其中4点为考虑强度退化后的屈服点。
将式(1)应用于此处考虑强度退化的Clough滞回模型,其强度退化关系为:
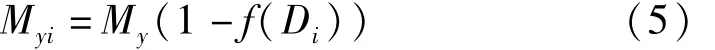
式中,Di是指向Myi某一时刻的损伤值。在确定式(5)中强度退化关系之前,需要确定弯矩-转角层面的损伤指标。
2 累积损伤模型
评价钢筋混凝土构件的损伤模型可以分为4种:① 非累积损伤模型;② 基于变形的累积损伤模型;③基于能量的累积损伤模型;④ 基于变形和能量的混合损伤模型。试验现象表明,钢筋混凝土构件的损伤与耗能和变形都有关系,而且损伤具有累积效应,因此第4种类型的损伤模型具有更好的适用性。其中广为应用的是Park等[12-13]提出的变形与能量混合的损伤模型:

式中,δm为最大位移,δu为构件的极限位移,β为组合系数,d E为耗能增量,Fy为屈服力。Park-Ang模型有两个缺点:① 上下界不收敛;② 没有考虑不同变形幅值下相同耗能所造成的损伤不同的试验现象。针对这两个问题,王东升等[14]提出了改进的Park-Ang模型:

其中βi是能量加权因子,与加载路径有关,δy为屈服位移。
Park-Ang模型是以力-位移关系为基础的。Kun-nath等[15]以 Park-Ang模型为基础,去掉可恢复变形,建立了弯矩-曲率损伤模型:

式中,θm是最大转角反应,θr是可恢复的转角变形,θu是极限转角变形,My是屈服弯矩,ET是耗能,β是强度退化函数。
文献[16]中以Park-Ang模型为基础,参考王东升等人的改进,提出了弯矩-转角层面的损伤模型为:

式(9)在文献[16]中可以被用于评价考虑三维受力(动轴力和双向弯曲)构件。本文考虑定轴力和单向弯曲的情况,式(9)各参量的计算可以由文献[16]中的计算方法简化得来。式(9)中,第一项为位移项损伤,第二项为耗能项损伤。β为组合系数。μ—θ,max是最大规格化转角延性系数。按式(10)计算,其中 θy、θu、θm分别为屈服转角、极限转角和最大转角(取绝对值):

式(9)中d Ep是塑性耗能增量,按式(11)计算,其中是弯矩-转角关系的弹性刚度:
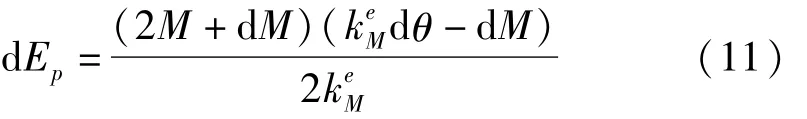
式(9)中Emon(θ)是单调加载至破坏时的塑性耗能。本文不考虑强化刚度,按理想弹塑性计算,Emon(θ)可以简化为:
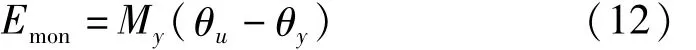
式(9)中 αmax是耗能修正项,按式(13)计算:

式(13)中,β1∈[0,+∞)为耗能修正项的指数,为常数;β2∈[0,+∞),为常数。
至此,可以看出,式(9)有三个模型参数 β、β1、β2,其中 β1、β2满足下式[16]:

参数的取值如下:β=0.1,β1=1.5,β2=2.5。性能状态的划分如表1所示:
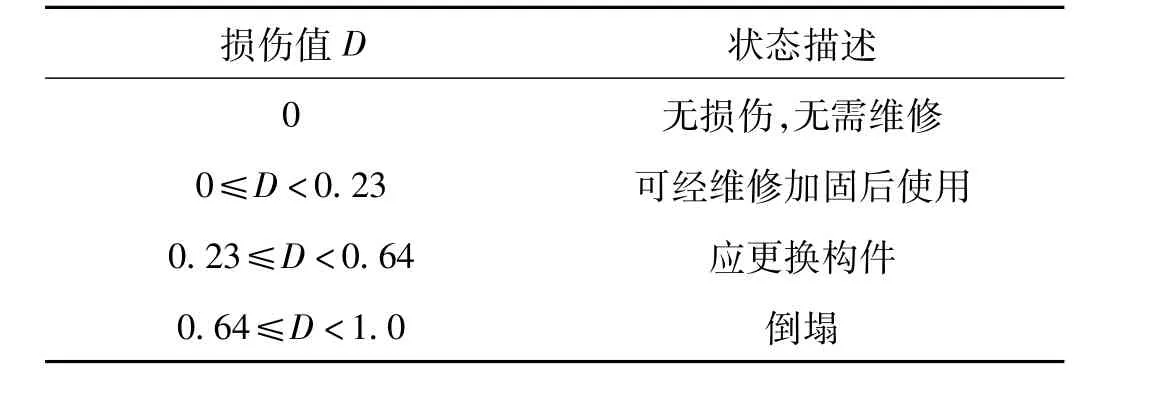
表1 性能状态的划分Tab.1 Classification of performance state
与Park-Ang模型相比,式(9)所示的损伤模型解决了上下界收敛问题,保证了损伤值单调不减的特征。因此本文采用此模型作为式(5)所示强度退化函数中的损伤指标。
3 地震反应与能力相互作用
国内外规范[3-6]中规定的地震反应计算和验算并未考虑反应与能力的相互作用。延性验算时,要求构件的变形延性满足既定的性能要求,并未考虑强度退化对构件能力的影响。其地震反应计算和验算流程如图3所示。
不考虑能力与反应相互作用的方法并不能准确地计算构件的地震反应,也不能准确地评价构件的损伤程度。第1节建立了强度退化的考虑方法,这可以用于计算过程中根据反应的大小,确定由于强度退化导致的构件能力的降低。第2节确定了累积损伤模型,这一指标可以用在强度退化函数中以评价强度退化的程度,同时也可以用于评估构件的破坏程度,为性能设计提供直接的定量标准。可以总结出考虑能力与反应相互作用的地震反应计算与验算流程,如图4所示。

图3 不考虑能力与反应相互作用的设计方法Fig.3 Design method without consideration of interaction between ability and response

图4 考虑能力与反应相互作用的设计方法Fig.4 Designmethod with consideration of interaction between ability and response
从上图可以看出,考虑能力与反应相互作用时,能力会随着地震反应的变化而变化。在考虑能力与反应相互作用的方法中,性能评价需要在计算反应的过程中同步进行,因为能力的降低是与损伤程度相关的。计算完成时,构件的损伤值也已计算完成,进而可以直接评估构件的性能。
上述过程可以在有限元程序中实现,若非线性迭代计算采用Newton-Raphson方法,其实现的基本流程如图5所示。其中灰底斜体字方框为考虑能力与反应相互作用方法所特有的。若采用的是弯矩-转角(例如式(9)所示的形式)或弯矩-曲率层面的损伤模型,那么这些特有的步骤都是在单元内部实现的,对整个有限元程序的框架没有影响,这将给有限元程序的编写或者二次开发带来方便。
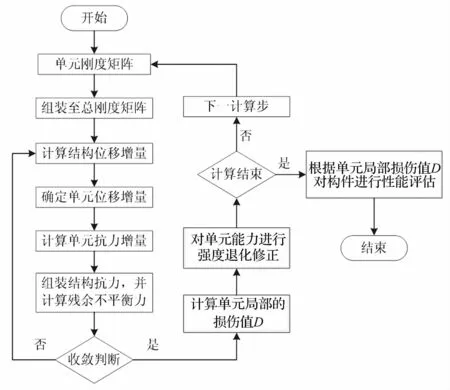
图5 考虑能力与反应相互作用的有限元流程图(修正的Newton-Raphson方法)Fig.5 Finite-Element Process with consideration of interaction between ability and response(Modified Newton-Raphson Mathod)
4 方法验证
第3节介绍了考虑地震反应与能力相互作用的考虑方法和有限元程序实现途径。这一节将介绍上述方法进行验证。在Opensees2.0.0版本源代码基础上进行二次开发,增加了能够考虑强度退化的塑性铰单元。
4.1 骨架曲线下降段的实现
以一个悬臂柱为例,柱顶施加单调增加的位移荷载,柱底设置一个塑性铰。其弯矩-转角骨架曲线如图6所示,其强化系数约为1%。
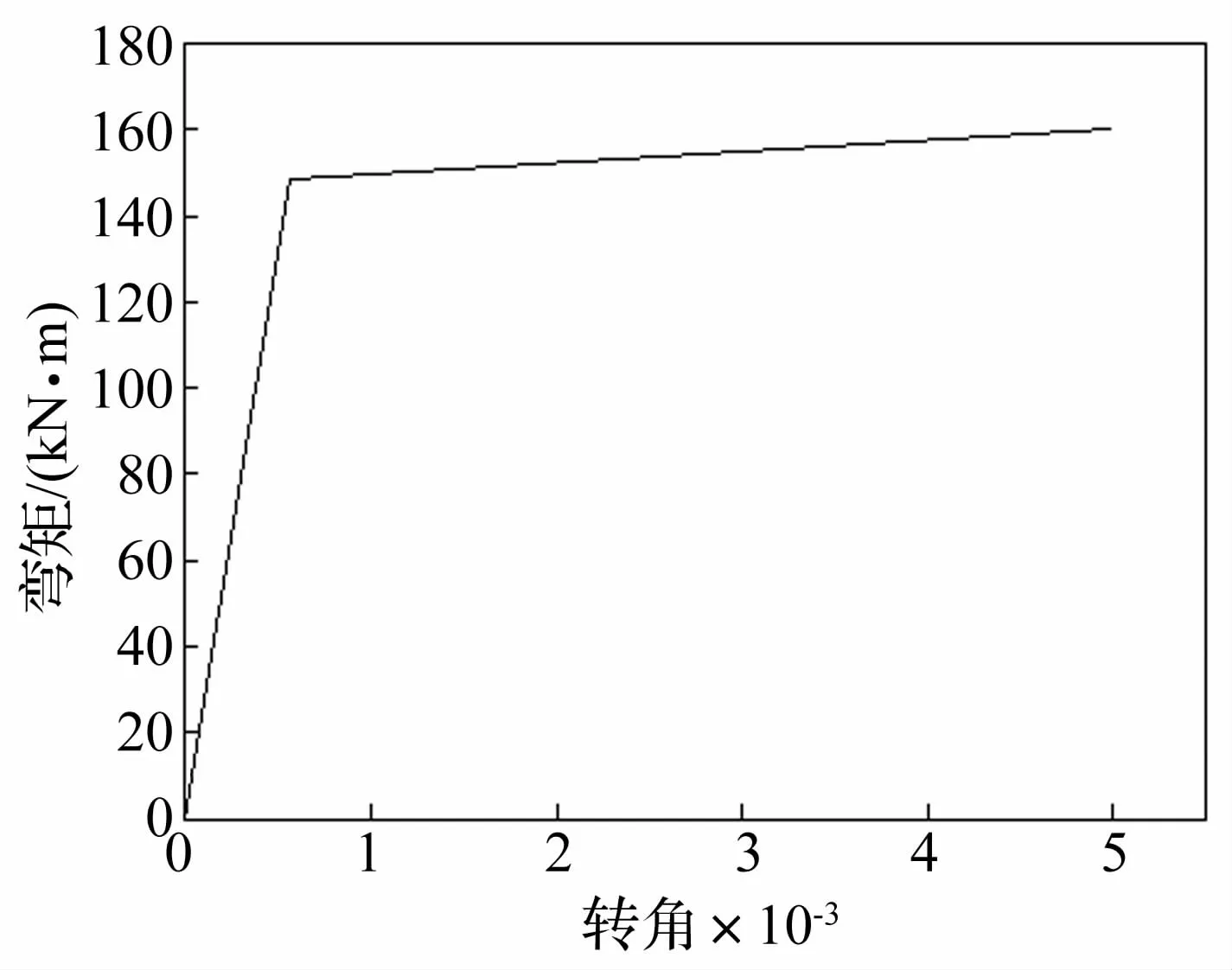
图6 弯矩转角骨架曲线Fig.6 Skeleton curve of Moment-Rotation
若其强度退化函数的定义为:
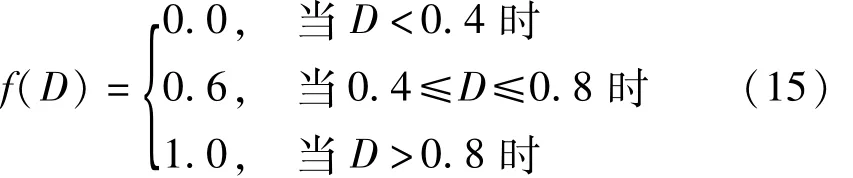
强度退化函数的图示如下图所示:
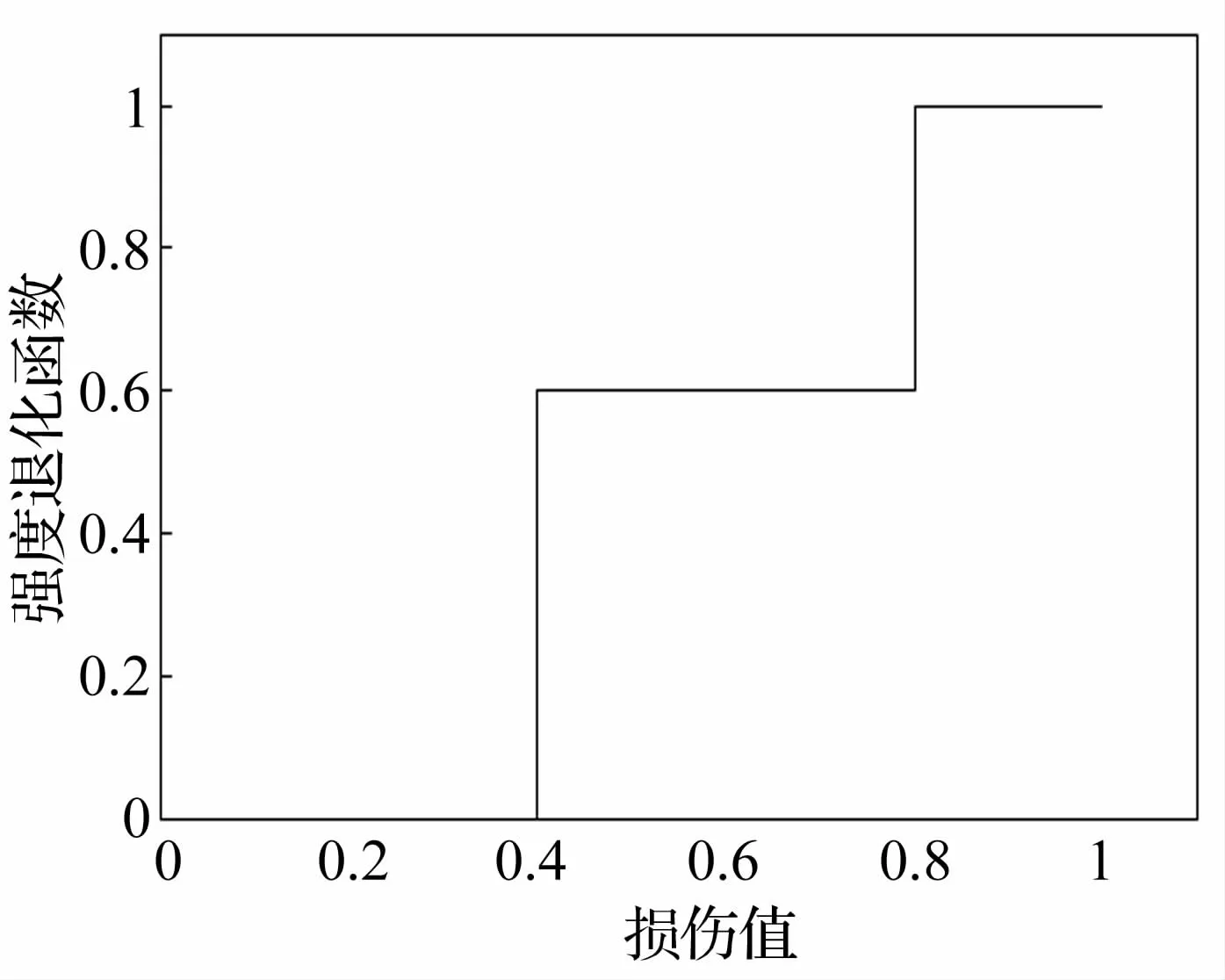
图7 强度退化函数的取值Fig.7 Value of strength degradation function
计算得到的损伤值D和强度退化函数值f(D)与转角之间的关系如图8所示:
计算得到的弯矩-转角关系如图9所示:

图8 损伤值D和强度退化函数值f(D)与转角之间的关系Fig.8 The relationship between damage,strength degradation function and rotation
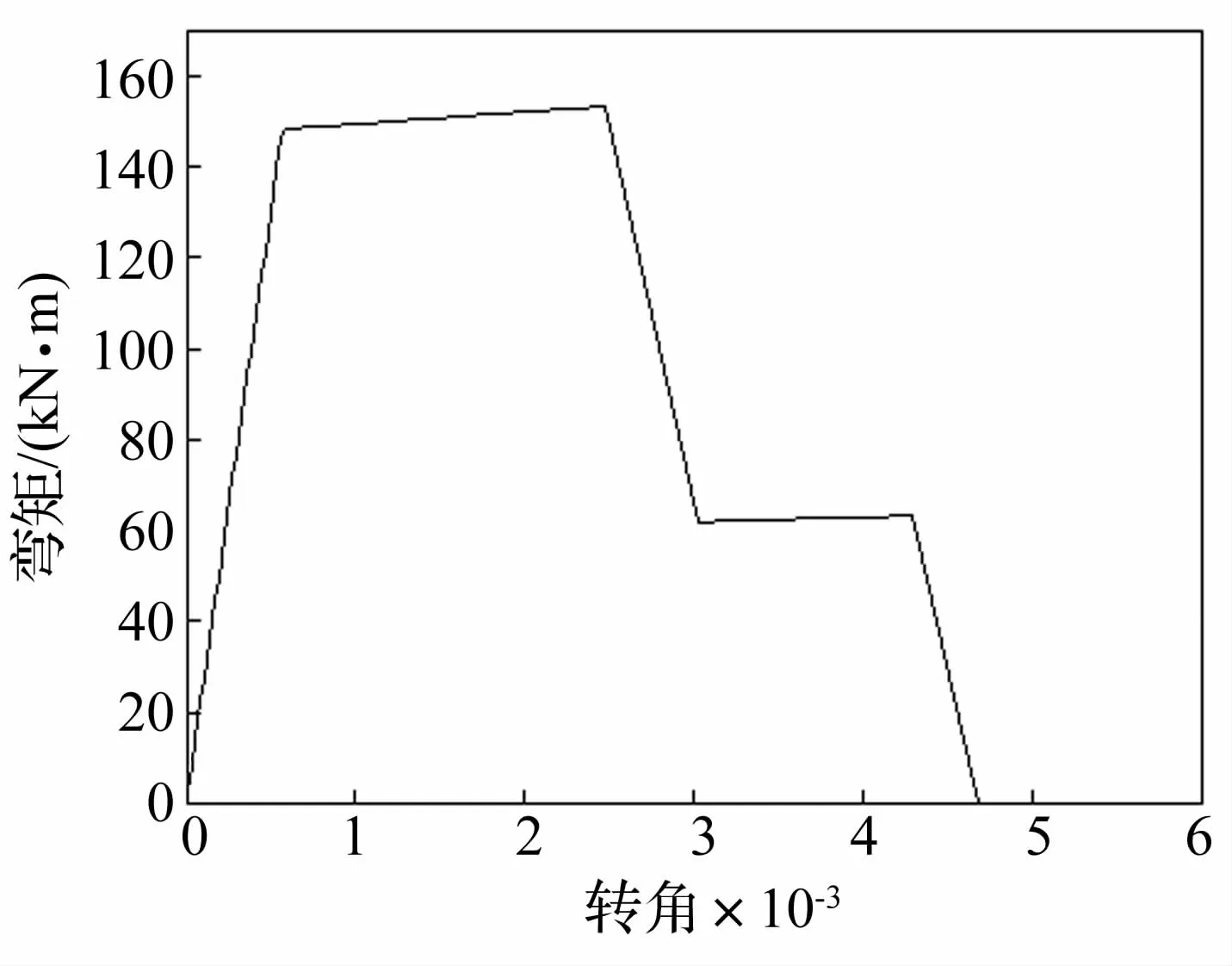
图9 弯矩-转角关系Fig.9 The relationship ofmoment-rotation
比较图6和图9可以发现,虽然骨架曲线是双线性的,没有负刚度段,但是考虑反应与能力的相互作用,通过定义合适的强度退化函数也可以实现类似于考虑强度退化的骨架曲线。在数值计算中,骨架曲线的负刚度段可能带来非线性求解方面的困难,本文所提的这种方式从一定程度上可以避免这种困难。
4.2 试验验证
Takemura和 Kawashima(1997)[17]进行的一组试验(试件编号为TP001~TP006)。该组试验6个试件的尺寸与配筋构造均完全相同。试件为钢筋混凝土悬臂柱。如图10所示,截面尺寸为400 mm×400 mm,截面有效高度h0=360 mm,加载点至地梁顶面距离L=1 245 mm,剪跨比为3.46。混凝土强度约为35 MPa,纵筋采用D13钢筋,屈服强度363 MPa,全部纵筋配筋率为1.58%。箍筋采用D6钢筋屈服强度为368 MPa,箍筋间距为70 mm,配箍率为0.57%。试验时柱顶施加157 kN的轴压力,轴压比约为2.89%。
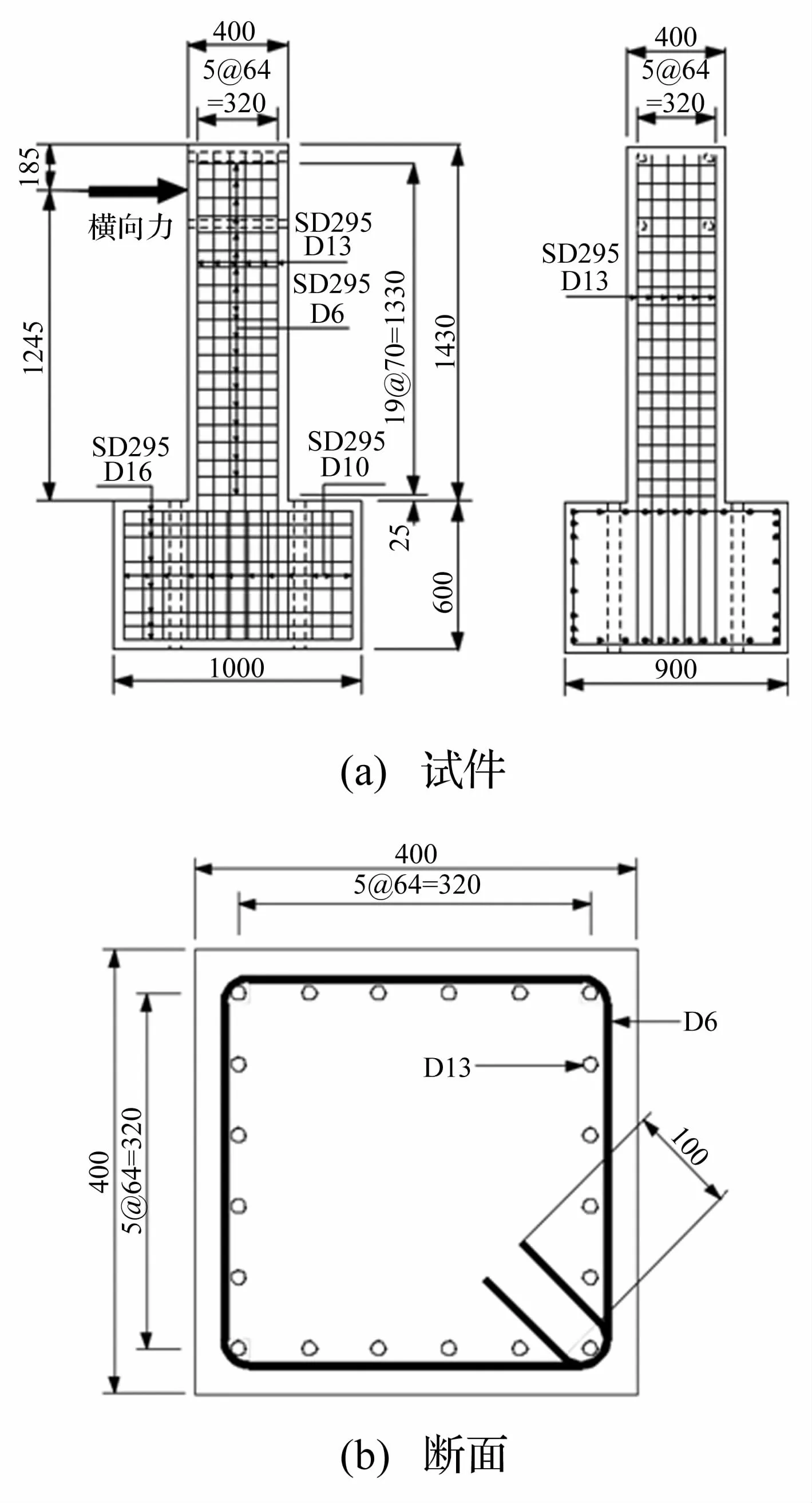
图10 试件和断面Fig.10 Test specimen and cross section
6个试件的加载路径均不相同,均采用位移控制,其加载模式如图11所示。
针对这组试验,文献[9]中确定了强度退化函数的简单形式:

式(16)中,λ为强度退化系数,取为 0.8。式(16)所示的强度退化函数采用了简单的线性形式,只有一个参数,易于确立。
各试件的试验结果与本文的数值模拟结果比较如图12所示,为了显示是否考虑反应与能力相互耦合对数值模拟结果的影响,分别列出了考虑强度退化和不考虑强度退化的数值计算结果。其中“数值模拟结果1”是考虑强度退化的结果,“数值模拟结果2”是不考虑强度退化的结果。图中的弯矩-转角的试验结果是根据力-位移的试验结果转化而来。

图11 加载路径Fig.11 Loading Hystereses
从图12中可以看出:
(1)虽然TP001~TP006的加载方式各异,但是总体来说,数值模拟结果1即考虑强度退化的结果与试验结果较为接近,这说明,对于试件TP001~TP006来说,式(16)所示的强度退化函数式是合适的,同时也说明本文考虑反应与能力相互作用的方式是可行的。
(2)数值模拟结果2即不考虑强度退化的结果与试验结果差别较大,这说明在某些情况下,不考虑损伤导致的强度退化将给数值模拟带来较大的误差。
5 结 论
本文首先说明了计算钢筋混凝土桥墩地震反应中考虑反应与能力相互作用的必要性,建立了考虑强度退化的方法。然后提出了考虑地震反应与能力相互作用的初步的设计流程和有限元程序的实现流程。最后通过两个方面的实例对本文方法进行了验证,主要成果有:
(1)提出了计算钢筋混凝土桥墩地震反应中考虑反应与能力相互作用的初步的设计流程和有限元程序的实现流程。
(2)结果表明,本文方法能够实现钢筋混凝土桥墩骨架曲线的负刚度段,从而避免数值计算上的困难;
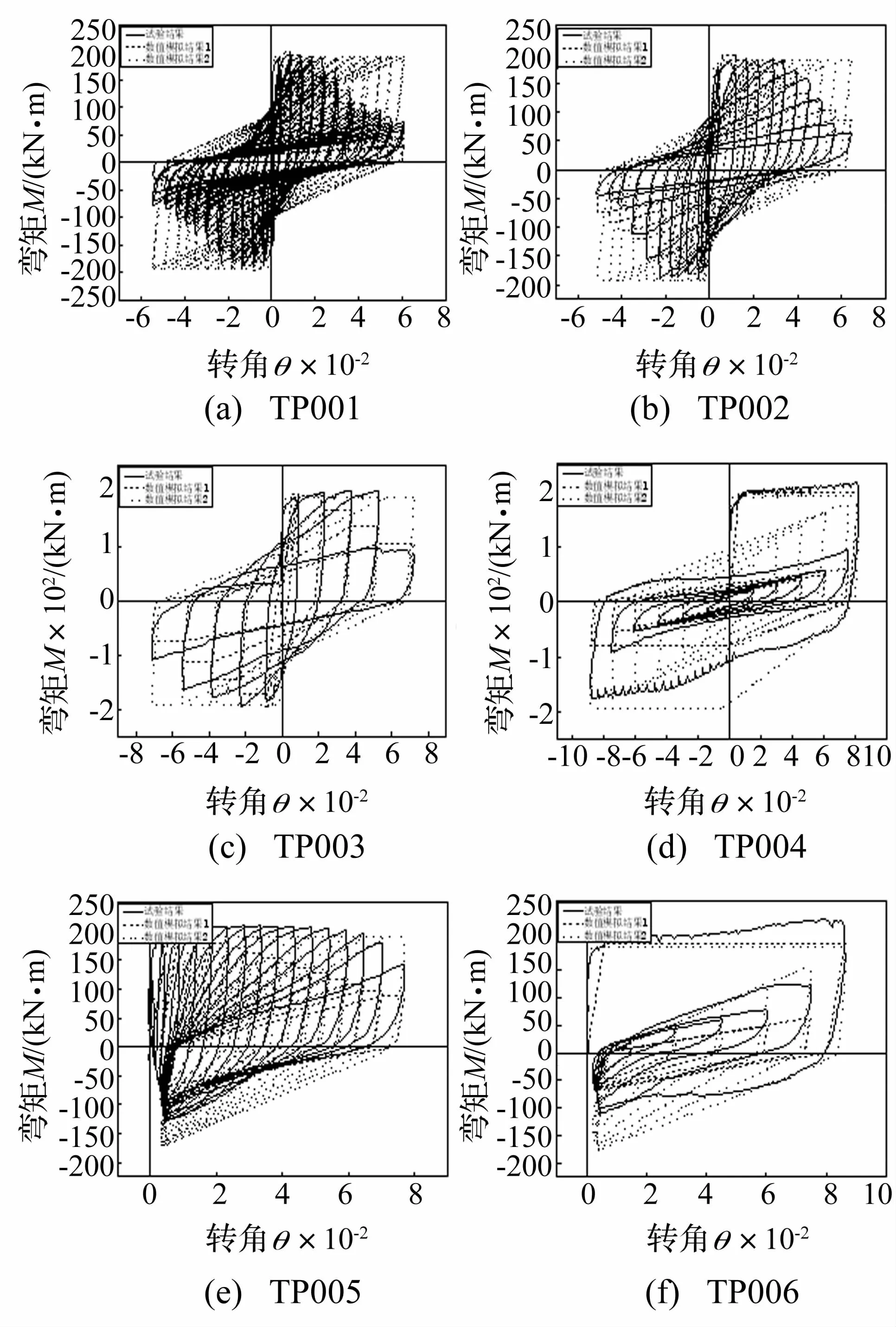
图12 文献[17]中试验结果和本文数值模拟结果Fig.12 Experimental results in Literature[17]and numerical results in this paper
(3)与试验结果的比较可以发现,本文方法能够较好地模拟钢筋混凝土桥墩不同加载模式下的试验现象。
以上结论表明,针对钢筋混凝土桥墩,本文所提出的考虑地震反应与能力相互作用的办法是可行的。
反应对能力的影响是多方面,除了本文重点讨论的强度退化现象之外,还有动轴力和双向弯曲现象。对于沿两个主轴方向的弯曲特性不相同的截面来说,空间转动的方向也会影响其能力的大小。另外,桥墩的非线性转动能力会随着轴力的变化而变化。因此全面地考察反应对能力的影响,还需要进一步考虑双向弯曲和动轴力的因素,本文的考虑办法和流程对这两种因素也是适用的。
[1]Bertero V V.The Need forMulti-level Seismic Design Criteria[C]//Earthquake Engineering Research at Berkeley-1996:Papers Presented at 11th WCEE.Report No.UCB/EERC-96/01.University of California at Berkeley,U.S.A.,1996:25-32.
[2]C Vision 2000 Committee. Performance-Based Seismic Engineering[C].Report prepared by Structural Engineers Association of California,Sacramento.California.U.S.A.,1995.
[3]中华人民共和国交通运输部.公路桥梁抗震设计细则(JTG/T B02-01-2008)[S].北京:人民交通出版社,2008.
[4]中华人民共和国铁道部.铁路工程抗震设计规范(GB 50111-2006)[S].北京:中国计划出版社,2006.
[5]铁道构造物等设计标准及解说——抗震设计[S].日本铁道技术综合研究所,1999.
[6]American Association of State Highway and Transportation Of-ficials.AASHTO Guide Specifications for LRFD Seismic Bridge Design [S]. Washington, DC, USA:AASHTO,2007.
[7]曲哲,叶列平.基于有效累积滞回耗能的钢筋混凝土构件承载力退化模型[J].工程力学,2011,28(6):45-51.QU Zhe,YE Lie-ping.Strength deterioration model based on effective hysteretic energy dissipation for RC members under cyclic loading[J].Engineering Mechanics,2011,28(6):45-51.
[8]Wang M L,Shah SP.Reinforced concrete hysteresismodel based on the damage concept[J].Earthquake Engineering and Structural Dynamics,1987,15(8):993-1003.
[9]郭进,王君杰.基于累积损伤的弯矩-曲率强度退化滞回模型[J].同济大学学报(自然科学版),2013,41(12):1767-1774.GUO Jin, WANG Jun-jie. Reinforced concrete strength degradation hysteretic moment-curvature model based on cumulative damage[J].Journal of Tongji University(Natural Science),2013,41(12):1767-1774.
[10]Clough RW,Johnston SB.Effect of stiffness degradation on earthquake ductility requirements[C]//Proc.2th Japan Earth.Engng.Symp.,Tokyo Japan,1966.
[11] Takeda T,Sozen M A,Nielsen N N.Reinforced concrete response to simulated earthquake[J]s.Journal of Structural Division,ASCE,1970,96(12):2557-2573.
[12]Park Y J,Ang A H S.Mechanistic seismic damagemodel for reinforced concrete[J].Journal of Structural Engineering,1985,111(4):722-739.
[13]Park Y J,Ang A H S,Wen Y K.Seismic damage analysis of reinforced concrete buildings[J].Journal of Structural Engineering,1985,111(4):740-757.
[14]王东升,冯启民,王国新.考虑低周疲劳寿命的改进Park-Ang地震损伤模型[J].土木工程学报,2004,37(11):41-49.WANG Dong-sheng,FENG Qi-min, WANG Guo-xin. A modified Park-Ang seismic damage model considering low-cycle fatigue life[J].China Civil Engineering Journal,2004,37(11):41-49.
[15]Kunnath S K,Reinhorn A M,Lobo R F.IDARC Version 3.0:A Program for the inelastic damage analysis of reinforced concrete structures[R].Technical Report NCEER-92-0022,National Center for Earthquake Engineering Research,State University of New York,Buffalo NY.
[16]郭进,王君杰,黄勇.Park-Ang损伤模型在弯矩-转角层面的三维拓展[J].世界地震工程,2013,29(4):141-146.GUO Jin,WANG Jun-jie,HUANG Yong.Three dimensional extension for Park-Ang damage model in moment-rotation level[J].World Earthquake Engineering,2013,29(4):141-146.
[17]Takemura H,Kawashima K.Effect of loading hysteresis on ductility capacity of reinforced concrete bridge pier[J].Journal of Structural Engineering,Japan,1997,43A:849-858.

