减震垫对导弹水下垂直发射横向振动的影响

孙船斌，马大为，朱忠领

（南京理工大学 机械工程学院，南京 210094）

导弹在水下平台垂直发射的方式具有饱和攻击、隐蔽性强、反应时间短等诸多特点［1］，出筒过程中导弹受到流体阻力［2－3］、气密环－减震垫的支撑以及摩擦作用［4］，使得导弹筒内运动的振动响应非常复杂。本文针对水下平台的导弹发射过程进行研究，将气密环－减震垫作为弹性减震垫来研究［5］，分析了导弹在筒内横向运动的自由振动特性，得到了导弹出筒过程的横向振动方程，在此基础上研究了减震垫的刚度、轴向尺寸和筒内分布对导弹横向振动频率、截面受力以及出筒姿态的影响。

1 动力学模型

根据动量与动量矩定理，在弹体坐标系中建立水下垂直发射过程的导弹横向运动微分方程［6－7］：

式中，x0、y0、θ0、m、Jzz、B、G分别是弹体坐标系下导弹质心的轴向位移、横向位移、俯仰角、质量、转动惯量、浮力和重力；xB是浮力对导弹质心的作用距离；λ22、λ26、λ66是流体的附加质量、静矩和转动惯量；YNa0、YNw0、Mza0、Mzw0是流体的法向力和俯仰力矩；Ys0、Mzs0是减震垫对导弹的横向作用力和作用力矩。

2 自由振动特性

建立平台坐标系，平台坐标系原点固定在发射平台上，与导弹质心初始位置重合，X轴正向沿着发射筒轴向上，Y轴正向与发射平台相对于海水的运动方向一致，Z轴由右手法则确定。

将式（1）、（2）的等号右边作为导弹在发射过程中所受的外力，并在发射平台坐标系中改写，得到导弹横向运动的自由振动方程：

式中，x、y、θ为发射平台坐标系下导弹质心的X轴方向位移、Y轴方向位移和绕 Z轴的俯仰角；m、Jzz、λ22、λ26、λ66与式（1）、（2）中一致；Fsi、Msi、Ys、Mzs为平台坐标系下第i个减震垫对导弹的横向作用力、力矩以及所有减震垫对导弹的横向作用力合力、合力矩，ki、xi、Hi为第i个减震垫的等效横向刚度、第i个减震垫上端相对于导弹质心的位置坐标以及减震垫与导弹实际作用的轴向长度，当导弹脱离第i个减震垫时，其作用长度Hi＝0。

结合式（7）、（8），对式（5）、（6）进行泰勒展开，并省略θ的高阶小量可得：

从式（11）、（12）中可以看出，C1、C2、D1、D2与减振垫的刚度ki、相对于导弹的位置xi以及实际作用的轴向长度 Hi相关，可以写成 C1／C2／D1／D2＝f（ki，xi，Hi），其中xi、Hi随导弹质心X轴位移x变化。

从式（14）可以看出 A1、A2、B1、B2与导弹的质量、转动惯量 m、Jzz以及流体的附加质量 λ22、λ26、λ66相关，m、Jzz不随导弹运动变化，而 λ22、λ26、λ66则是导弹轴向位移 x的函数［8］。

由式（19）可知导弹在筒内某一位置的横向自由振动的频率 w＝g（A1，B1，B2，C1，D1，D2），因此 w与减振垫的刚度、轴向尺寸以及减振垫在筒内分布相关，且随着导弹的轴向运动而改变。

3 振动方程

结合式（15）、（16），在平台坐标系下，导弹筒内运动的受迫振动方程由式（3）、（4）写成：

式中其中M是系统质量矩阵，K是系统刚度矩阵，v是导弹横向运动的物理坐标，f1、f2为系统所受外力外力矩。YNa、YNw、Mza、Mzw分别是平台坐标系下的流体法向力和俯仰力矩。

由式（19）可得导弹横向运动的1阶2阶频率w1、w2，代入式（17）、（18）可得发射过程导弹横向振动的特征矢量 V1、V2：

可将导弹的横向运动的物理坐标v表示为：

式中，q1（t）和 q2（t）是导弹横向振动的广义主坐标，q1（t）和 q2（t）是振动频率 w1，w2的周期函数且相互独立，将式（25）代入式（15）、（16）得：

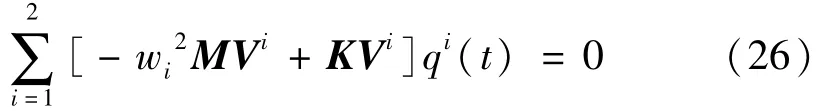
结合式（11）至（14），可知矩阵 M、K实对称，可知当（23）、（24）关于矩阵 M、K对称，则由式（27）可得［9］：

式中 ＜N1，N2＞表示向量 N1、N2的内积；Mp、Kp的物理含义为系统p阶模态质量、刚度。

由式（28）、（29）可知 Mp、Kp仅是导弹 X轴方向位移 x的函数，将式（25）代入式（20），结合式（28）、（29）可得广义主坐标下导弹横向运动v的振动方程：

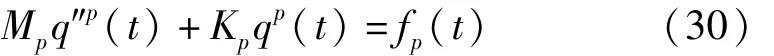
导弹在筒内的运动过程可以分成无数个微元时段det T，在微元时段det T内，导弹轴向位移变化所引起的系统质量矩阵M和刚度矩阵K的改变量为微小量。可以假设在微元时段内M、K的值不变，且由前一微元时段ti－1末导弹的横向运动状态作为导弹在当前微元时段ti的初始状态；同时由式（21）和式（22）可知，外激励fti可由 ti－1末导弹的运动状态近似得到。结合式（25）和（30），由导弹在 ti－1结束时的横向运动状态 v0可得到导弹在筒内当前时刻t的横向振动，其中ti＜t＜ti＋det T：

式（31）中Vp是导弹横向振动的p阶特征矢量，式（32）中v0是导弹在 ti－1结束时横向的运动状态，qp0为 ti－1结束时导弹横向运动的广义坐标。

4 算例和结果分析

由式（31）、（32）可知，导弹在筒内任意时刻的横向振动可以分成2部分：其一，从ti－1到ti，导弹在X轴方向的运动x引起导弹横向振动频率w的突变，同时ti－1结束时的导弹横向运动状态将作为初始状态突然加载，而产生导弹横向的自由振动；其二，在ti内，由外部激励f1、f2引起的导弹横向的受迫振动。

由式（19）、（31）可知，导弹横向运动的振动特性与减震垫参数密切相关，为研究减震垫对导弹横向振动的影响，给出发射条件如下：导弹质量2 000 kg，质心位置距导弹底部3．5 m，导弹轴长及发射筒长均为8 m，发射平台相对海水水平速度vt＝2 m／s。根据8道减震垫的轴向长度、横向的等效刚度以及在筒内的分布位置，分别建立5个工况，如表1。在各工况中，第8道减震垫上端位于发射筒口，其余减震垫按数字倒序依次在筒内从上到下分布。各工况的导弹轴向运动速度、加速度等内弹道参数保持一致。文中所用数据均采用国际单位制，如角位移、角速度、力和力矩单位分别为rad、rad／s、N和 N·m。

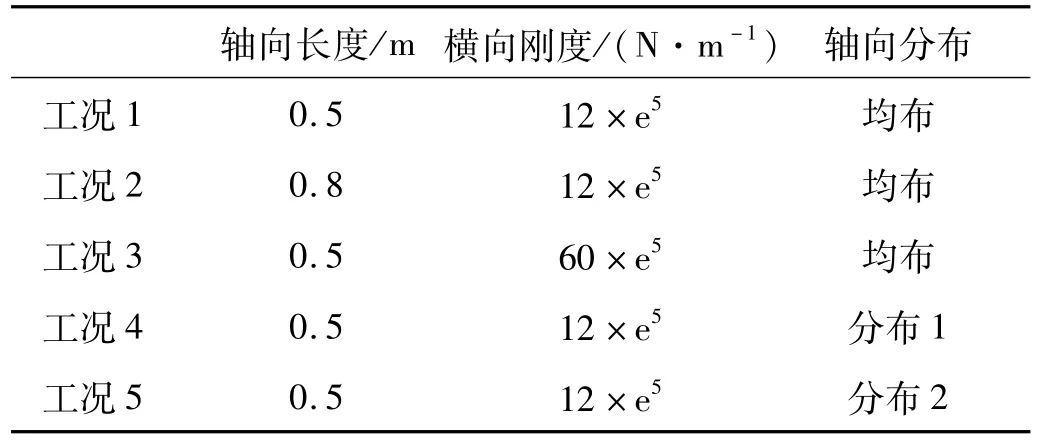
表1 各工况的减震垫参数Tab．1Parameters of pads for working conditions

图1 系统1阶2阶振动频率Fig．1 Curves of first and second frequency for the system

图1为出筒过程中各工况导弹横向振动的1阶2阶频率 w1、w2，从式（11）、（12）、（13）和（14）可知，A1、A2、B1、B2中 λ22、λ26、λ66关于导弹轴向位移 x的斜率是连续的，而C1、C2、D1、D2关于导弹轴向位移 x的斜率在导弹脱离减震垫的过程中存在间断点，且各间断点的位置位于导弹运动到各减震垫的下端位置时，从而导致导弹横向振动频率w关于时间的斜率也存在间断点，如图1所示。图1中（a）、（b）分别为工况1、2、3的1阶2阶频率曲线，从中可以看出，由于增大了减震垫的轴向长度、减震垫的横向刚度，导弹横向振动的1阶2阶频率也增大了；从工况2的频率曲线可以看出，增大减震垫的轴向长度，导致减震垫的间隙减小了，使得导弹的频率w斜率相邻的两个间断点位置更近，而使曲线更为光滑；从工况3的频率曲线可以看出，增大减震垫的横向刚度，导致导弹的频率w斜率在间断点前后变化增大，使得曲线起伏程度变大。图1中（c）、（d）分别工况1、4、5导弹横向振动的1阶2阶频率，从中可以看出，改变减震垫在筒内的分布位置，会相应地改变1阶2阶频率斜率间断点的位置。

图2 导弹出筒姿态Fig．2 Curves of pitch angle and angle velocity for themissile

图3 指定截面的剪切力和剪切力矩Fig．3 Curves of cross section shear stress and shear torque

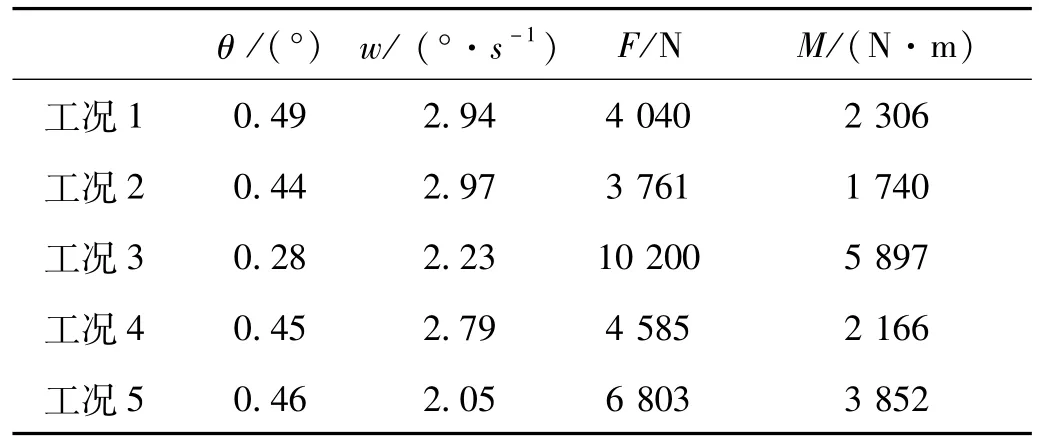
表2 出筒时刻计算结果Tab．2 The computation results for the outlet of them issile

图2是出筒过程中导弹的俯仰角和俯仰角速度，图3是出筒过程中指定截面的剪切力和剪切力矩，其中剪切力F与计算值符号相反。表2是各工况导弹出筒时刻的姿态以及指定截面的剪切力、剪切力矩峰值。

从图2（a）、（c），图 3（a）、（c）以及表 2中可以看出，增大减震垫长度可以使得导弹出筒姿态曲线平滑，能够较好地抑制指定截面剪切力和剪切力矩峰值；增大减震垫刚度能够较明显地减小出筒姿态，但会增大导弹俯仰角速度的震荡，而且会增大指定截面的剪切力和剪切力矩峰值。

从图2（b）、（d），图 3（b）、（d）以及表 2中可以看出，工况4和工况5的曲线显示了减震垫分布对导弹横向振动的影响。工况4中第6、7、8道减震垫间隙为0，工况5中第4、5、6道减震垫间隙为0，相比于前者，后者的导弹俯仰角速度震荡程度更大，且指定截面的剪切力和剪切力力矩峰值更高。

5 结 论

本文推导了水下平台导弹出筒的横向振动方程，分析了出筒过程中导弹的横向振动特性，主要得出以下结论：

（1）导弹出筒过程的横向振动由两部分组成：其一，由导弹振动频率w的突变引起的横向自由振动；其二，由外力引起的导弹横向受迫振动。

（2）导弹横向振动的1阶2阶频率曲线反应了导弹振动频率的时变特性，减震垫的间隙导致频率曲线的斜率存在间断点。

（3）增大减震垫的轴向尺寸，导弹的姿态及指定截面受力均较好；增大减震垫的横向刚度能明显减小导弹出筒的俯仰角和俯仰角速度，但会显著增加导弹姿态的震荡和导弹的截面受力，从而增加导弹出筒的不稳定性和不安全性；应当避免减震垫的间隙在发射筒内末端分布过大，否则会引起导弹出筒姿态较大的震荡以及较高的截面受力。

［1］赵世平，蔡体敏．横向流对潜艇垂直发射导弹的影响［J］．船舶力学，2006，10（4）：33－37．ZHAO Shi-ping，CAI Ti-min．Effects of lateral flow to the missile vertical launched from a submarine［J］．Journal of Ship Mechanics，2006，10（4）：33－37．

［2］Waugh JH，Stubstad GW．Hydroballistiesmodeling［R］．AD－A007529．1975．

［3］Burgdorf O．Hydrodynamics of unsteady underwater launched missile with trailing cavities and cross-flow drag［R］．AIAA，Fluid Dynamics，Plasma Dynamics，and Lasers Conference，19th，Honolulu，1987．

［4］尚书聪，孙建中，秦丽萍．潜载导弹水下发射出筒横向动力学特性研究［J］．振动与冲击，2012，31（23）：82－86．SHANGShu-cong， SUN Jian-zhong， QIN Li-ping． Lateral dynamic behavior of a underwater missile launched out its launch tube［J］．Journal of Vibration and Shock，2012，31（23）：82－86．

［5］裴，张宇文，袁绪龙，等．潜载导弹垂直发射横向振动特性仿真分析［J］．兵工学报，2009，30（8）：1056－1060．PEIXuan， ZHANG YU-wen， YUAN XU-long， et al．Simulation and analysis on the lateral vibration characteristic of vertical launching for submarine-borne missile［J］．Acta Armamentarii，2009，30（8）：1056－1060．

［6］张宇文．鱼雷弹道与弹道设计［M］．西安：西北工业大学出版社，1999．

［7］刘乐华，张宇文．深海垂直发射内弹道研究［J］．舰船科学技术，2004，26（1）：24－26．LIU Le-hua，ZHANG Yu-wen．Study on trajectory for vertical launch under deep-sea［J］．Ship Science and Technology，2004，26（1）：24－26．

［8］郜冶，陈宇翔，刘乾坤．潜射导弹出筒过程水动力计算［J］．计算机仿真，2011，28（9）：86－89．GAO Ye，CHEN Yu-xiang，LIU Qian-kun．Hydrodynamic computation for submarine-launched missiles emerging from a submarine［J］．Computer Simulation，2011，28（9）：86－89．

［9］芮筱亭，来峰，陆毓琪，等．多体系统传递矩阵法及其应用［M］．北京：科学出版社，2008．