高温下不同比例钢筋混凝土柱力学性能相似性有限元分析

蔡新江，夏玮超，毛小勇，田石柱

(1. 苏州科技大学土木工程学院，江苏，苏州 215011；2. 苏州科技大学江苏省结构工程重点实验室，江苏，苏州 215011)

研究工程结构耐火性能时，一般希望采用足尺模型(原型)进行耐火试验，采用足尺模型的优点在于可以直接得到构件的耐火极限、极限承载力及极限变形等高温力学性能指标，缺点在于足尺模型试验费用高昂，同时以目前的火灾试验设备能力来说，也只能覆盖部分常规尺寸的足尺构件试验，对于超高层、大跨度结构等来说，依然无法进行足尺模型试验。缩尺模型具有低成本、易于调节试验参数等显著优势，目前已经广泛应用于结构静动力试验、抗震试验、抗风试验等领域[1−2]，并能较好反映原型结构的力学行为。因此，基于模型相似理论，研究缩尺模型和足尺模型之间高温下时间和温度场相似关系，力求通过模型耐火性能试验结果反推原型耐火性能，进而降低工程结构耐火试验成本。

目前国内外针对火灾试验中的缩尺行为进行了理论与试验研究。王进军等[3]针对足尺标准燃烧室建立缩尺燃烧室数值模型，并基于火场相似关系调整火源功率，模拟表明缩尺燃烧室的火场可以较好地反映足尺燃烧室内部温度分布。陈适才等[4]设计钢框架缩尺模型和缩尺火场进行整体结构火灾反应试验，试验表明高温下钢框架缩尺模型和原型的承载力和稳定性能等力学特性满足相似关系。邱仓虎等[5− 6]通过调整缩尺模型的防火涂料厚度和升温曲线，对有防火保护的H 型钢缩尺模型进行高温下数值模拟和试验，结果表明缩尺模型可以正确地反映足尺模型的温度场、结构变形和耐火极限。王永超等[7]通过修正H 型钢柱缩尺模型的受火时间和表面换热系数使得缩尺模型和足尺模型的温度场相似，并通过修正缩尺模型的刚度比、荷载比和偏心距使得两者耐火极限相同。王君等[8]基于FDS 软件建立空间火场的1/20 缩尺模型，并对缩尺模型的参数进行无因次化，研究表明，1/20 缩尺模型和足尺模型的火源功率、温度、能见度和烟气层高度等关键火灾参数均具有较高的吻合性。刘利先等[9− 10]设计不同截面尺寸的钢筋混凝土轴压柱，并基于截面尺寸比值调整升温时长和荷载，通过试验得出了构件耐火极限和截面尺寸比值的关系。Connor 等[11]针对钢筋混凝土结构，得出缩尺模型升温曲线调整方法并进行火灾试验，试验表明调整缩尺模型升温曲线可以使得缩尺模型和足尺模型的温度场始终保持一致。吕昊然等[12]基于文献[11]升温曲线调整方法得出0.7 和0.5 缩尺比例下的缩尺模型升温曲线，依据相似理论建立钢筋混凝土简支梁缩尺模型进行数值模拟和耐火试验，并与足尺模型耐火性能进行对比，证明高温下钢筋混凝土梁的缩尺模型可以较好地反映原型的温度场、跨中挠度和耐火极限。

针对足尺钢筋混凝土模型柱，本文基于相似理论分别建立2/3、1/2、1/3 缩尺模型并进行耐火性能分析，对比缩尺和足尺模型的温度场、结构变形、耐火极限和极限承载力等高温下力学性能指标，力求能从缩尺模型反推得原型结构的耐火性能。

1 热力响应相似关系

1.1 结构相似关系

依据相似理论，缩尺模型和足尺模型在满足几何相似，荷载相似、质量相似、时间相似、刚度相似和边界条件相似的前提下，才可将两者对应的力学性能指标进行对比分析，因此需要对缩尺模型的物理量根据相似关系进行严格换算。本文参照《建筑抗震试验规程》[13]中拟静力试验缩尺模型相似关系进行取值，当缩尺模型和足尺模型采用同种材料时，相似关系如表1 所示。

表1 缩尺模型相似关系Table 1 Similarity relation of scale model

1.2 高温下时间相似关系

缩尺模型和足尺模型的热力响应满足相似关系的前提是在任意时刻两者的温度场需保持一致，因此需要对缩尺模型的升温曲线进行调整，将升温曲线分为升温时长和对应各时间点的温度(炉温)两方面进行调整，文献[6]认为缩尺模型的等效受火时长tm取决于缩尺模型几何相似常数SL和足尺模型的升温时间tp，其关系式如下：

由式(1)可得，缩尺模型实际升温时长是由足尺模型升温时长按照缩尺比例进行缩放得到。

1.3 温度场相似关系

式(1)确定了缩尺模型的实际升温时长，同时也需要对缩尺模型的炉温进行调整，热流密度公式如下：

由于在火灾试验中，同时考虑热对流和热辐射参数对热流的影响相对比较困难，所以一般选择不考虑热对流或者热辐射的影响来进行简化。本文采用文献[11]推导的热辐射公式，即认为热流密度由热辐射控制，假定炉辐射换热系数和试件表面的辐射换热系数一致，则由式(3)和式(6)联立可得：

针对缩尺模型进行耐火性能分析时，式(7)中由于缺少足尺模型表面温度数据，导致无法求得缩尺模型的炉温，因此需要通过有限元方法对足尺模型进行温度场计算，得出足尺模型表面温度Tw,p。本文将有限元温度场计算结果进行拟合，提出一种足尺模型表面温度计算公式：

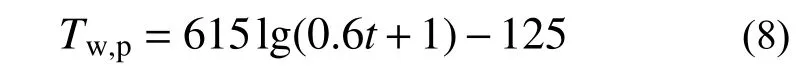
式中，t为足尺模型升温时长。以Z1 足尺模型柱由ISO 834 标准升温曲线进行四面受火150 min 为例，由式(8)所得足尺模型表面温度和有限元温度场计算结果对比如图1 所示。

图1 拟合足尺模型表面温度对比Fig. 1 Comparison of surface temperature of fitting full -scale model

结合式(1)和式(7)可以得出缩尺模型升温曲线，并由式(3)可知缩尺模型的热流密度要高于足尺模型，即缩尺模型炉温要高于足尺模型，故两者升温曲线如图2 所示。

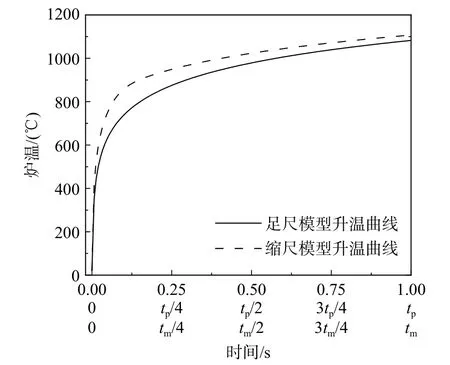
图2 缩尺模型升温曲线Fig. 2 Temperature rise curve of scale model

2 足尺模型和相似模型有限元建模

2.1 计算模型

设计12 组钢筋混凝土足尺模型柱，设计参数见表2，其中，各模型均采用ISO834 标准升温曲线升温，且受火高度和柱高保持一致，Z1～Z10 为轴心受压柱，Z11 和Z12 柱为偏心受压柱，进行热力耦合时，轴压柱需在非加载端设置固定约束，在加载端仅不约束加载方向位移分量，其余转动及位移分量均保持约束，偏压柱在轴压柱约束基础上，还需放松柱两端的转动位移方向的转动分量。依据表1 所述缩尺模型相似关系分别建立2/3、1/2 和1/3 缩尺模型，研究不同比例下缩尺模型和足尺模型之间的温度场以及高温下力学性能的相似关系。

表2 钢筋混凝土柱设计参数Table 2 Design parameters of reinforced concrete column

基于ABAQUS 进行有限元建模时，混凝土和钢筋高温下应力-应变关系按Lie 等[14]规定取值，高温下弹性模量按陆洲导[15]建议取值，热工参数包括热膨胀系数、比热、热传导率等均采用欧洲规范EC2[16]建议取值，取钢筋混凝土柱受火面对流换热系数为25 W/m2·K，非受火面受热系数为9 W/m2·K，综合辐射换热系数为0.7。温度场计算时，设置钢筋单元类型为DC1D2 两结点传热连接单元，混凝土单元设为八结点线性传热实体单元，且钢筋与混凝土之间设为绑定(Tie)连接，进行热力耦合计算时，设置钢筋单元类型为T3D2 两结点线性三维桁架单元，混凝土单元设为C3D8R八结点线性实体单元，且需将钢筋内置于混凝土中以完成力学计算。为验证有限元模拟的准确性，以Lie 等[17]中试验柱1 的实验结果进行模拟对比，结果如图3 所示，由图可知，有限元模拟所得轴向变形位移曲线和试验结果基本吻合，因此，本文所用混凝土和钢筋高温本构关系、热工参数和建模方法较为准确。

2.2 升温曲线

以模拟柱Z1 在ISO834 标准升温曲线下四面受火升温150 min (9000 s)为例，取足尺模型跨中截面外表面处温度作为式(7)所述试件外表面温度并通过式(7)可得其2/3、1/2 和1/3 缩尺模型对应足尺模型升温时间的升温曲线如图4 所示。

图4 缩尺模型原型升温曲线Fig. 4 Prototype heating curve of scale model

依据温度场相似关系，需通过式(1)把缩尺模型升温时间调整为66.7 min 和37.5 min 后才可进行数值模拟，缩尺模型实际升温曲线如图5 所示。

图5 缩尺模型实际升温曲线Fig. 5 The actual temperature rise curve of the scale model

由图4 可知，2/3、1/2 和1/3 缩尺模型的升温曲线均高于足尺模型升温曲线，且1/3 模型升温曲线在三条曲线中对应各点温度最高，原因是缩尺模型和足尺模型的热流密度成反比，即截面尺寸越小，模型热流密度越大，炉温越高。

3 有限元结果分析

3.1 截面温度分析

影响钢筋混凝土柱截面温度场的主要因素为截面尺寸、受火时间及受火面数，其中，受火时间对截面最终温度高低影响较大，对截面温度场分布影响较小，即对缩尺模型和足尺模型的温度场相似性影响不大，因此以表2 中Z1、Z7 及Z9四面受火柱为例，依据2.2 节所述升温曲线分别对缩尺模型和足尺模型进行升温数值模拟，得出3 组柱跨中截面温度云图如图6 所示。

图6 柱截面温度云图 /(℃)Fig. 6 Temperature nephogram of column section

由图6 可知，三组钢筋混凝土受火柱缩尺模型和足尺模型的温度分布较为一致，截面尺寸、受火面数对温度分布影响较小，证明建立的缩尺模型升温曲线可以保证缩尺模型和足尺模型温度场一致。

选取Z1 系列柱跨中截面任一受火面处1/10 处混凝土、柱截面中心混凝土和任一受火面处纵筋温度进行分析，结果如图7 所示。

图7 Z1 柱截面不同位置处温度曲线Fig. 7 Temperature curves at different positions of Z1 column section

由图7 可知，对于柱截面1/10 处混凝土，在升温约33 min (2000 s)后，缩尺模型的温度略高于足尺模型，且最终温度相差16 ℃左右。对于中心混凝土，缩尺模型和足尺模型的温度时间曲线基本保持重合，缩尺模型的温度略低于足尺模型，且随着缩尺比例的减小，缩尺模型的温度和足尺模型相差越大。由于Z1 系列柱在三个位置处的温度时间曲线均基本重合，因此可以认为缩尺模型和足尺模型的温度场在任意时刻均保持一致。

3.2 柱顶轴向位移分析

在温度场相似情况下，调整柱截面尺寸、轴压比、配筋率、长细比、受火面数和偏心率，以此分析不同初始条件下的缩尺模型与足尺模型的结构相似性，将缩尺模型轴向变形时间曲线均按缩尺比例原型化后的模拟结果如图8 所示。

由图8 可知，在约33 min (2000 s)后，缩尺模型的轴向变形均略小于足尺模型。通过3.1 节分析可知缩尺模型和足尺模型的温度场存在较小的差异，而升温时长33 min 时炉温均在800 ℃左右，缩尺模型和足尺模型内部的温度相对也较高，导致其力学性能退化较大，因此缩尺模型和足尺模型的温差会使得两者轴向变形产生较大的误差。Z3 和Z7 两组轴向变形曲线中，对应的1/2 和1/3 缩尺模型的轴向位移明显低于足尺模型，两组柱的膨胀变形相对较大。由表2 可知，由于提高了纵筋配筋率和加大了截面尺寸，Z3 和Z7 柱相当于提高了柱的承载能力，但轴向荷载未发生变化，导致其荷载比偏小，对该试件变形相似性产生一定影响，但影响较小。Z11 和Z12 系列偏压柱，缩尺模型轴向变形略低于足尺模型，但两者轴向变形曲线基本吻合。

图8 原型化柱轴向变形曲线Fig. 8 Prototype column axial deformation curve

因此，轴压和偏压情况下，足尺模型和缩尺模型高温下的轴向变形均具有较好的相似性。在工程模型试验中，依据相似关系建立的缩尺模型可以较为精确地反映出足尺模型在常温下的力学性能，因此，在保证缩尺模型和足尺模型温度场相似的情况下，两者高温下的力学性能也应当具备相似关系。

3.3 耐火极限分析

根据《建筑构件耐火试验方法第1 部分：通用要求》[18]规定，柱达到耐火极限的判定准则之一是柱的轴向压缩变形大于h/100 mm，其中h为柱的受火高度。对各组柱升温360 min 后进行耐火极限分析，以Z1 和Z2 两组柱为例，将缩尺模型的轴向变形和受火时间按缩尺比例原型化后，两组柱的轴向变形时间曲线如图9 所示。

对于原型化后的Z1 和Z2 系列柱，其轴向变形达到42 mm 时可认为柱达到耐火极限，由图9可知，三种缩尺比例下，缩尺模型与足尺模型的轴向变形均较为吻合，其中，Z1 系列柱在升温183 min 后，由于高温下柱的力学性能退化明显，且1/3 缩尺模型和足尺模型之间存在相对较大的温差，使得1/3 缩尺模型的轴向变形和足尺模型产生较大的误差，导致其耐火极限下降。各组柱原型化后的耐火极限和对应误差如表3 所示。

图9 柱耐火极限轴向变形曲线Fig. 9 Axial deformation curve of column fire-resistance limit

由表3 可知，各组柱对应的缩尺模型的耐火极限均接近于足尺模型。仅Z9 系列柱的耐火极限差距较大，其1/2 和1/3 缩尺模型的耐火极限和足尺模型分别相差7.2%和10.9%，在三面受火情况下，缩尺模型和足尺模型的温度差相对较高，使得Z9 系列柱在高温下的力学性能出现较大的差异，导致耐火极限相差较大。

表3 各组柱耐火极限计算结果Table 3 Calculation results of fire-resistance limit of each column

3.4 耐火承载力分析

基于位移增量加载方法对12 组柱求解高温下轴压承载力和位移的关系，设置各组足尺模型位移的加载速率为1 mm/1 min，依据相似关系，对足尺模型加载速率进行调整并应用于缩尺模型柱，即对于2/3、1/2 和1/3 缩尺模型分别采用0.44 mm/0.67 min、0.25 mm/0.5 min 和0.11 mm/0.33 min 位移加载速率，位移加载曲线如图10 所示。

图10 位移加载曲线Fig. 10 Displacement loading curve

由于构件加载至临近破坏时，有限元计算增量会急剧减小并最终低于最小计算增量，导致有限元进程中断，此时，构件已经产生过大的轴向压缩变形，因此本文在有限元计算中断时即认为各组柱达到极限破坏状态，将缩尺模型的位移和承载力进行原型化处理后，各组柱的高温下承载力位移曲线如图11 所示。

图11 原型化柱承载力-位移曲线Fig. 11 Load-bearing displacement curves of prototype columns

由图11 可得原型化后各组柱的承载力-位移曲线基本重合，其中缩尺模型的曲线均略高于足尺模型，且缩尺比例越小，承载力位移曲线相差越大。由3.1 节和3.2 节分析可知，各组柱的缩尺模型和足尺模型的温度场均存在细微的差异，且缩尺模型的轴向变形均略小于足尺模型，可以认为这部分温差使得缩尺模型在高温下的力学性能退化程度较低，即具有更高的承载能力，因此各组缩尺模型的承载力位移曲线均高于足尺模型。各组柱原型化后的极限承载力和对应误差如表4所示。

由表4 可知，缩尺模型的极限承载力均略高于足尺模型，各组柱对应的2/3、1/2 和1/3 缩尺模型和足尺模型的极限承载力误差分别在4%、6%和10%左右。由3.1 节可知，缩尺比例越小，缩尺模型内部混凝土温度越低，导致比例越小的缩尺模型高温下力学性能退化程度越低，因此缩尺比例越小，极限承载力越高。

表4 各组柱高温下极限承载力计算结果Table 4 Calculation results of ultimate bearing capacity of columns in each group at high temperature

整体上各组柱的承载力-位移曲线基本保持重合，高温下的极限承载力误差不大，可以认为缩尺模型和足尺模型高温下的极限承载力具有较好的相似性。

4 结论

本文研究不同比例下钢筋混凝土柱缩尺模型和足尺模型高温下的温度场以及力学性能的相似性，得出以下结论：

(1) 采用本文所示升温曲线升温时，钢筋混凝土柱缩尺模型和足尺模型温度场分布具有相似性。

(2) 不同截面尺寸、轴压比、配筋率、长细比以及受火面数情况下，缩尺模型和足尺模型结构变形具有相似性，但随着荷载比的减小，相似性变差。

(3) 缩尺模型和足尺模型的耐火极限具有相似性，仅在三面受火情况时某个模型的耐火极限误差达到11%。

(4) 对缩尺模型位移加载速率调整后，缩尺模型和足尺模型的耐火极限承载力满足相似关系，但缩尺比例越小，承载力位移曲线相差越大。

(5) 现有研究中缺少基于尺寸效应影响的材料高温本构关系，因此本文对缩尺模型和足尺模型采用同种强度等级的材料本构关系，无法完全准确反映出尺寸效应对材料强度的影响，将在后续工作中进一步进行研究。