运动方程自适应步长求解的高性能Galerkin 时程单元初探

袁 驷，袁 全

(清华大学土木工程系，土木工程安全与耐久教育部重点实验室，北京 100084)

结构动力响应问题是工程计算的重要课题，常用的时程积分方法更是最有效的方法之一，但其计算效率、计算精度、数值稳定性等均与步长的选择和优化相关[1−2]，因此自适应步长求解也成为近几年研究的难点和热点之一。就自适应求解而言，有对离散解进行误差估计并建立自适应算法[3− 4]的研究，但在时域上逐点按最大模控制误差的高效自适应求解更为困难，也极为少见，而这恰是本文追求的目标。

袁驷等依据有限元数学原理[5]提出的单元能量投影[6−8](element energy projection，简称EEP)法是一种非常有效的有限元后处理的超收敛算法，可用于进行逐点误差估计和精度修正。该EEP 算法已应用于一维[9−10]、二维有限元[11]，乃至三维有限元[12]，并且提出一类基于EEP 技术的Galerkin有限元时程积分的自适应方法[13]。该法对常规单元构建了单步法递推公式，用EEP 超收敛解进行误差估计，创建了自适应步长算法公式并给出了数学证明[14]，进而再次运用EEP 技术对结点位移修正[15]来实现高效的自适应求解。

文献[16]将二阶运动方程等效地转换为一阶方程组初值问题(以下称为一阶运动方程)，构建了一类无条件稳定的Galerkin 常规单元。但该类单元采用结点位移修正技术后，蜕变为有条件稳定[16]，故需要进一步探索一类无需结点位移修正的、超高结点精度的新型单元，以期实现更加高效、更加稳定、更加可靠的按最大模控制误差的自适应步长求解算法。

本文基于一阶运动方程的非自伴随性质，尝试提出一种通过对检验函数凝聚而提高单元端结点精度的新型单元——凝聚单元。本文算法相比于文献[16]的常规单元，在保持了无条件稳定的前提下，对任何次数单元，其端结点位移的收敛阶均可提高2 阶，极大提高了结点位移精度和自适应步长求解的效率。

1 问题描述与常规Galerkin 有限元

1.1 问题描述

为了表述简明，本节以单自由度常系数运动方程为例，其可以归结为如下二阶常微分方程初值问题：

其中：

可见，将二阶运动方程转化为一阶方程组后，Galerkin 法中对检验函数降低了要求，属于H0空间即可，本文将充分利用这一性质。

1.2 常规Galerkin 有限元

由于可以逐单元步长积分求解，不失一般性，仅考虑两端结点坐标为(0,h)的典型单元e。注意，对于一阶运动方程的Galerkin 弱形式式(5)，若将试探函数uh取为m¯次多项式，则检验函数vh通常取为低一次的m¯−1次多项式，即：

1.3 EEP 超收敛公式

2 凝聚单元——高性能单元

本节是本文的重点，将提出一套新型高效单元——凝聚单元。研究发现，对于上述的一阶运动方程的Galerkin 常规单元作少许巧妙的改进，便可在不提高单元次数且保持无条件稳定的前提下，将各次单元端结点位移的精度普遍提高2 阶。本法可概括为“三部曲”，即“同次、凝聚、升阶”。简述如下：

1) 同次，是指将检验函数vh的次数由m¯−1次取为和试探函数uh相同的m¯次，亦即为vh增加了一个自由度，但并没有增加单元的次数；

2) 凝聚，是指利用伴随问题凝聚掉vh的一个自由度，使其还原为原本的自由度数，但更加逼近精确的检验函数，亦即构造出凝聚检验函数v∗，其余则按常规有限元步骤求解；

3) 升阶，是指由此得到的单元端结点解答的精度可比同次数常规单元解答的精度普遍提升2 阶。

为了帮助理解该单元的构成，本节先对精确检验函数做一说明。

2.1 精确检验函数

2.2 凝聚单元的构成

2.3 凝聚单元性质

凝聚单元具有诸多优良性质，列举几点如下：

1) 凝聚单元，求解运动方程是无条件稳定的，求解一般初值问题是A 稳定的；

2) 凝聚单元，单元内部位移精度仍然为O(hm¯+1)阶；

4) 对于线性元，凝聚单元结点位移精度翻倍，为O(h4)阶；

3 自适应步长

本文采用与文献[13, 16]相同的自适应策略和目标，即在精确解u未知的情况下，事先给定误差限tol，寻求一个优化的单元步长分布，使得这些单元上有限元解答uh按最大模度量，逐单元满足：

在确定和调整步长上，同样采用与文献[13, 16]相同的步长公式，即：

4 数值算例

本文采用符号计算软件Maple 计算有阻尼简谐运动、无阻尼自由振动以及多自由度的算例，以验证本法的有效性。为方便起见，本文引入误差比，即误差与误差限之比，记作e¯h。

例1. 有阻尼简谐运动

计算数据为：m=1，k=1，c=0.04，f=sin(0.2t)，u0=0，v0=1 ，T¯ =256 s，初始步长h0=0.5。表1 为三次元的相关计算结果。图1、图2 为三次元、tol=0.001的数据结果。由表1 可知，本法的误差得到有效控制，最大误差比均小于1。改变单元长度次数很少，最多不到5 次，最大最小单元长度比合理，体现了本法的高效性。由图1、图2 可见，本法步长分布合理，误差分布均匀，且多数单元误差在上下限区间内。

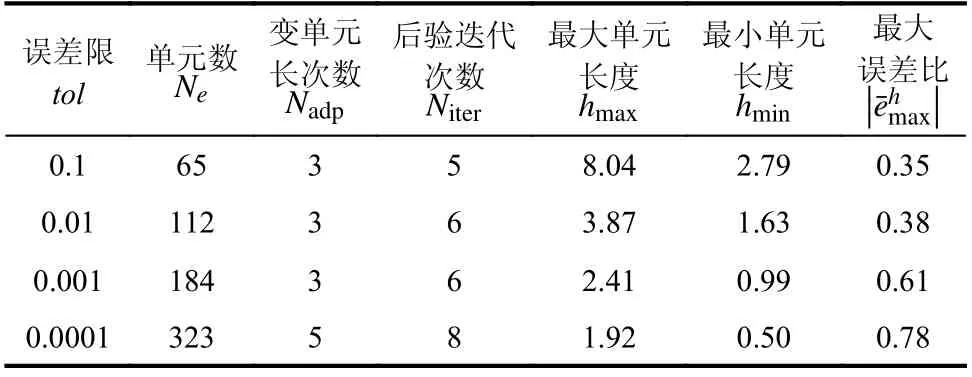
表1 有阻尼简谐振动数据 (256 s，三次元)Table 1 Results of damped harmonic motion (256 s, Cubic)

图1 例1 步长分布图Fig. 1 Step-size distribution for example 1

图2 例1 单元位移误差比图Fig. 2 Displacement errors of elements for example 1

例2. 无阻尼自由振动

计算数据为：m=1，k=1，c=0,f=0，u0=0，v0=1 ，T¯ =256 s，初始步长h=0.5。表2为三次元的相关计算结果。图3、图4 为三次元、tol=0.001的数据结果。由表2 和图3 可知，本法对无阻尼自由振动只需调整步长一次，即可在全部时域上满足误差要求，这符合无阻尼自由振动自身的特性。由图4 可见，其误差分布几乎是呈周期分布。

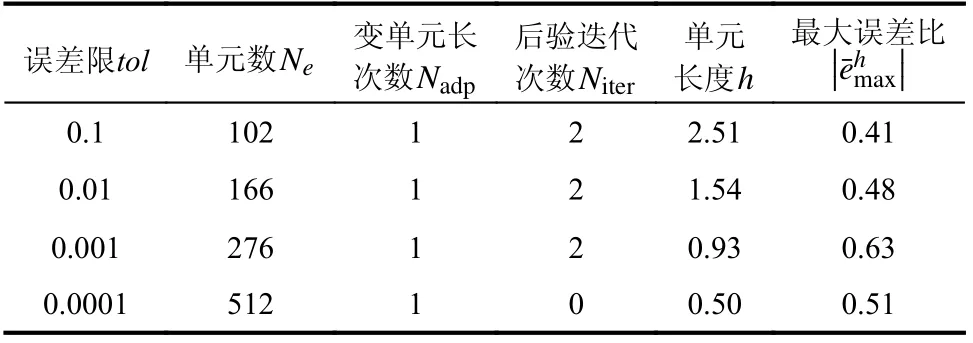
表2 无阻尼自由振动数据 (256 s，三次元)Table 2 Results of undamped free vibration (256 s, Cubic)

图3 例2 步长分布图Fig. 3 Step-size distribution for example 2

图4 例2 单元误差比图Fig. 4 Displacement errors of elements for example 2

例3. 多自由度简谐振动

图5 例3 步长分布图Fig. 5 Step-size distribution for example 3

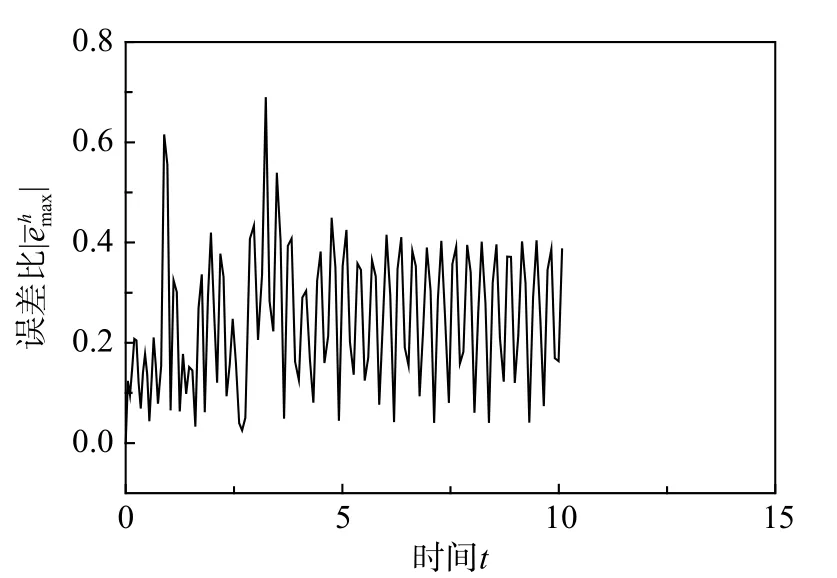
图6 例3 单元误差比图Fig. 6 Displacement errors of elements for example 3

物理模型来源于3 层剪切型框架结构，计算数据为：性质与单自由度相似，步长分布均匀且合理。由表3 和图4 可见，由于其多自由度特性，尽管自适应次数和迭代次数仍然较少，但是多于单自由度问题。由图5 可知，误差分布多在误差上下限区间内。

表3 多自由度简谐运动计算数据(256 s, 三次元)Table 3 Results of multi-degree-of-freedom system motion (256 s, Cubic)

5 结论

本文以运动方程为例，提出了凝聚单元。该单元巧妙地利用一阶运动方程的非自伴、低检验函数的性质，在保持无条件稳定的前提下，以低次单元获得超高阶收敛的结点位移精度，不失为一类高性能自适应步长时程单元。