基于双死区设计的空气悬架高度滑模控制方法

尹 航，邬明宇，李雪冰，吕靖成，杜永昌，梁冠群，危银涛

(清华大学汽车安全与节能国家重点实验室，北京 100084)

可控悬架的出现为车辆性能的进一步改善带来了可能。相比于全主动悬架[1]，半主动悬架能耗更低，控制简便，应用越来越广泛[2]。其中，空气悬架作为一种实现高度调节的半主动悬架，具有一定的刚度和阻尼变化特性，有利于调节车身姿态稳定，越来越受到人们的关注。

空气悬架控制的有效实现依赖于精确的动力学模型[3−13]，文献中常见的模型有Li 等[3− 4]提出的几何学图解与有限元分析模型，Oda 等[5]、Shimozawa等[5− 8]提出的等效力学模型和Berg 等[9− 10]提出的实验数据辨识模型等。上述动力学模型一般假设气体发生多方变化，其指数需要数据拟合或经验确定，不易有效反映高度控制过程中气室的充放气物理过程。

在空气悬架高度控制过程中，为了减少目标高度附近系统频繁充放气控制切换及对操纵稳定性、平顺性和元件寿命的影响，需要在控制系统中设置一个高度死区范围。然而，文献中大多只设置单个死区[14−15]，系统仍有可能在死区边沿出现频繁的控制律切换，这种单死区设置的缺陷改进少有报道。

空气悬架的高度控制策略需要保证足够的响应速度和精度。江洪等[16]、Prabu 等[17]提出的PID 控制策略、Gao 等[18]提出的模糊逻辑控制等利用高度偏差构造系统的控制策略，方法简易实用，而控制律较少结合系统内部动力学特性。一些非线性控制策略和智能控制策略，如Ma 等[14]、Sun 等[15]对整车姿态稳定进行的模型预测控制，Chen 等[19]对动力学系统线性化后提出的线性二次最优控制，Shan 等[20− 21]基于模糊自适应学习的神经网络算法，H∞控制[22]、滑模变结构控制[23]、反演控制[24]等也得到应用。这些控制方法多与系统特性进行深入结合，取得了较好的控制效果，但控制律有时较为复杂或无明确的表达形式，不便于实际应用，还可能受到算力的限制。

本文针对上述问题展开研究，主要进行以下几部分工作：1) 利用热力学第一定律，建立不依赖于多方变化规律、充分考虑各种能量变化的空气弹簧气室非线性模型，并进行实验验证，进而完成四分之一空气悬架系统动力学模型搭建；2) 提出一种高度控制的双死区设置方法，相比于单死区设置，在保证控制精度的同时，减少车高动态变化的干扰以及控制频繁切换问题；3) 在上述工作基础上运用滑模控制理论，提出一种与系统动力学特性充分结合、形式较简，且能适应外界扰动输入和系统动力学参数变化的鲁棒性控制策略，并利用MATLAB/Simulink 仿真平台对动力学模型和控制策略的有效性进行了分析和检验。

1 空气悬架系统建模

1.1 空气悬架气路系统简述

一种乘用车空气悬架系统气路结构如图1 所示，包含4 个空气弹簧、蓄压器、空压装置及相对应的控制阀等主要部分。蓄压器或空压装置作为高压气源，当需要向某个空簧充气时，高压气源控制阀与空簧充气阀打开，高压气流流入气室，使该位置的车身高度增加；当某个空簧需要放气时，空簧放气阀打开，气室内的气体流入大气，使该位置的车身高度降低。此外，空压装置还可以对蓄压器充气，保证其中的高压状态。

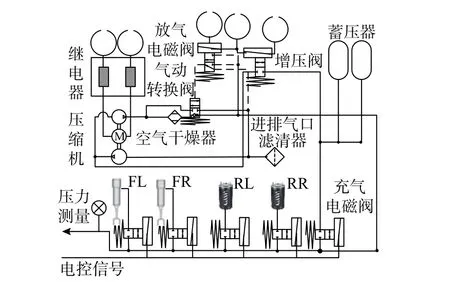
图1 整车气路结构Fig. 1 Gas path structure of full car

相比于整车模型，四分之一车辆二自由度系统结构简单，能较好地反映系统的基本垂向动力学特性，尤其是空气悬架的车高调节过程。因此，本文接下来将以四分之一车辆系统作为主要研究对象，其基本结构如图2 所示，气流往来于气源和气室之间。空气悬架系统建模一般包含部分假设[25]，以下将基于上述文献中假设，并分别对其中的气体多方变化规律假设、管路节流孔假设进行放宽，对空气弹簧气室、连接管路建立更精确的模型，最终完成完整的四分之一车辆动力学建模工作。

图2 四分之一系统简化结构Fig. 2 Simplified structure of quarter car

1.2 空气弹簧气室的精确模型与实验验证

空气弹簧气室是空气悬架动力学模型中最关键的部分，具有高度非线性，气体状态变化复杂，且在控制过程中气室内的气体量会发生变化，因此根据定质量气体多方变化规律确定气体状态存在一定偏差。采用热力学第一定律进行分析可以清楚反映不同物理过程对应的能量影响，过程完备，准确性更高。

以气室内的气体作为控制体，对气体状态方程进行微分：

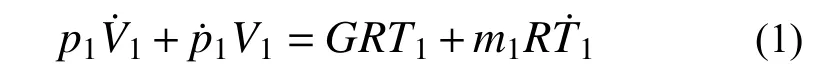
式中：p1、V1、m1、T1、R分别表示气室内的绝对压强、体积、质量与温度以及气体状态常数；G为从外界输入控制体的质量流量，即m1的变化率，以质量增加(充气)为正，减少(放气)为负，无控制指令时，气室处于被动隔振状态，G=0。

根据热力学第一定律的微分形式：

式中，4 个微分量分别表示外界传递给气室的热量、外界对气室所作体积功、外界输入气体质量带来的能量和气室气体内能的增量。其中，微元时间dt内外界传递的微元热量与外界和气室的温度差成正比：

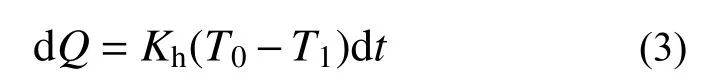
式中，Kh、T0分别表示气室的导热系数与大气温度。外界对气室所做的微元体积功为：

式中，CV表示空气的定容比热容。

将以上各微元表达式代入式(2)，再除以dt，可得：

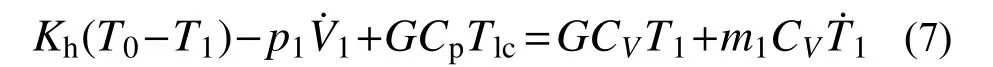
结合式(1)、式(7)，假设气体很快达到均匀状态，以T1代替Tlc，气囊产生的作用力FAS为相对压强与有效面积A(空簧气室的作用力与气室内相对压强的比值)的乘积：

式(8)即空簧气室模型的微分控制方程，从压强和温度两个方面刻画了空簧气室的特性。其中γ 为空气的比热容比，pa为大气压。气室的几何性质也会影响动力学特性，气室的体积V1和有效面积A的变化规律可通过试验确定，这里假设它们随高度线性变化[26]：

式中：V10、A0为静态初始状态下气室的体积与有效面积；Vh、Ah表示体积和有效面积随高度的变化率；(z2–z1)表示气室高度的增加量。

在此基础上利用Mechanical Testing & Simulation公司生产的力学性能测试平台对某型号空气弹簧进行实验，图3、图4 展示了实验平台设备与原理。将空簧上端固定，调节下端位置到一定高度并充气至初始压强值。实验中不进行充放气，通过下端的液压作动器给定位移激振，测量空簧产生的垂向力，数据由计算机进行采集读取，部分实验参数见表1。

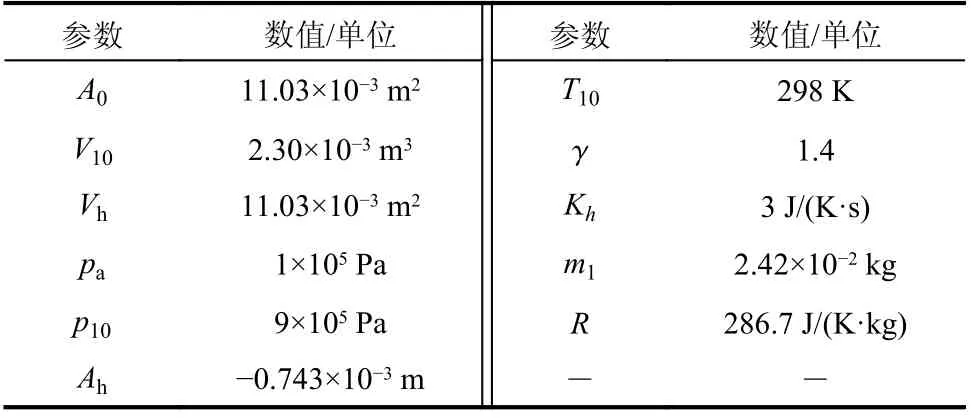
表1 空气弹簧气室实验部分参数Table 1 Parameters in air spring chamber experiment

图3 实验平台设备Fig. 3 Experiment apparatus

图4 实验原理Fig. 4 Experiment principle

以1 Hz 的正弦激振作为给定位移，分别测试了3 组不同振幅下的受力响应情况，其与根据上述理论仿真的结果对比如图5～图7 所示。可见实验与理论仿真结果均较好地体现了空簧的非线性特征，这证明了该空簧气室建模方法的合理性。

图5 气室模型仿真与实验结果对比-振幅26 mmFig. 5 Comparison of chamber model simulation and experiment result - amplitude 26 mm

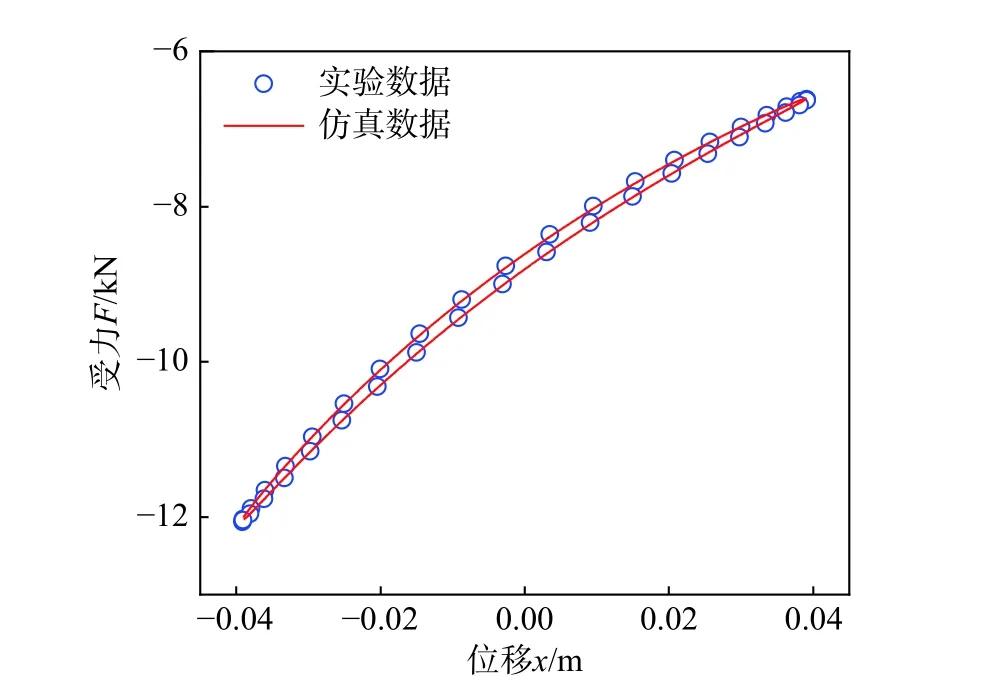
图6 气室模型仿真与实验结果对比-振幅39 mmFig. 6 Comparison of chamber model simulation and experiment result - amplitude 39 mm

图7 气室模型仿真与实验结果对比-振幅52 mmFig. 7 Comparison of chamber model simulation and experiment result - amplitude 52 mm

1.3 四分之一空气悬架车辆模型的实现

下面在上述空簧气室建模的基础上，完成四分之一车辆模型的其他部分建模。直接控制车身高度的质量流量G与气路连接管路模型密切相关。目前对空气悬架系统的连接管路建模大多等效为一个节流孔，质量流量为压强的线性或非线性代数表达式[6− 7,26]；或结合一维等熵流动假设，建立考虑气流音速状态流量壅塞现象的节流孔式模型[27−28]。但很多情况下管路的长度和截面积不一定很小，高速气流的惯性效应不可忽略，有必要对整个管路进行动力学分析，建立节流管式连接管路模型，如考虑一些线性化假设的文献[29]。下面结合空气动力学知识，推导出一种更精确的节流管式管路模型质量流量公式。

管道内的流体流动如图8 所示，气流从上流高压pu处流向下流低压pd处，管长为L，x坐标处长度为dx、质量为dm的气流质量微元密度为ρ，两端的压强、流速分别为(p,u)和(p+(∂p/∂x)×dx,u+(∂u/∂x)×dx)。视流动为一维流动，微元质量的动力学方程为：

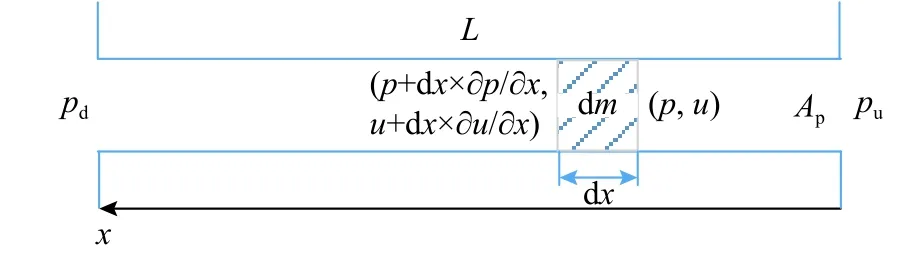
图8 节流管式管路模型动力学分析Fig. 8 Dynamic analysis of throttle pipe model in pipeline

式中：Ap为管路截面积；f为微元在流动中的微元摩擦阻力，通过沿程损失计算：

式(14)即为基于管路气流动力学分析的质量流量微分模型。

此外，考虑到流速的有限性和管路阻力效应，实际气流还会存在一定的时滞和耗散效应。根据流动中速度、密度变化率的小量假设[30]，前述的微元动力学方程和流动连续性方程可以整理为带耗散项的二阶偏微分波动方程：

式中：Rt为单位长度上的管道阻力特性；a为声速。在给定管路起始端流量边值G0(t)的情况下，可以求出管路末端因损耗和时滞造成的最终流量表达式Ge(t)[31]：

式(14)、式(16)确定了节流管式管路模型的质量流量动力学规律与损耗和时滞效应。同时，在本文建立的模型中假定高、低压气源处在恒定状态，压强分别保持为恒值ph和大气压pa，温度均为大气温度[25]。

相比于采用金属弹簧的悬架系统，空气悬架车身不再有忽略簧上重力影响的所谓“平衡位置”。据此，在垂向车辆建模中引入一项等效力Δ：

式中：FAS0、FAS分别表示初始静止状态时和动态情况下空簧气室产生的实际作用力；Mg为簧上重量。等效力Δ与传统悬架以“平衡位置”为原点、忽略簧上重力的悬架弹簧相对作用力的特性相似，可在动力学方程中等效，无需改变传统悬架的动力学分析方法：

式中：Mt、C、Ct、Kt分别表示非悬挂质量、减振器阻尼系数、轮胎的等效阻尼和等效刚度；z2、z1、z0分别表示悬挂质量位移、非悬挂质量位移和路面位移激励，均以初始高度位置为原点。

综上所述，可得较完备的空气悬架四分之一车辆动力学状态方程(见附录1)。式中q为路面扰动，是对路面速度激励的描述，质量流量G作为该动力学系统物理层面的控制输入，将通过下面叙述的控制策略实现对系统车高的控制。

2 空气悬架的高度控制策略

2.1 高度控制的双死区设置方法

空气悬架系统的闭环控制逻辑如图9 所示。车辆垂向模型反馈的车身高度等状态量作为被控量，通过控制器产生连接管路中节流电磁阀的等效比例开度信号u作为系统输入，由连接管路模型转换为充放气时的气流质量流量，改变气室内的气体量，使车身高度达到控制要求。直接控制量u为脉宽调制 (pulse width modulation, PWM) 信号，取值为0 或1，通过改变调制波占空比α 的形式驱动on-off 模式工作的电磁阀达到等效的比例开度控制效果。

图9 空气悬架系统闭环控制基本逻辑Fig. 9 Basic logic of air suspension close-loop control

空气悬架控制策略既要保证速度与精度，又要抑制目标高度附近的连续振荡，需要设置一定死区，当车高偏差小于一定范围时即停止控制，防止频繁的控制模式切换影响平顺性与执行器寿命。然而，死区可能影响控制的稳态误差，其边界附近也可能产生振荡。鉴于此，本文提出一种双死区设置方法，在目标高度上下Δs高度范围内设置小死区Ds，在目标高度上下Δs到Δl范围内(Δl>Δs>0)设置大死区Dl。车高调节时，若初始高度h0的偏差绝对值大于Δl，系统将进行控制操作，直至高度偏差进入小死区范围才停止控制。但当系统高度稳定在小死区内，由于扰动等因素车高进入大死区时，系统不进行控制操作，除非高度偏差进一步离开大死区，系统才进一步控制高度偏差到小死区内。即：当系统高度位于大死区外，进行控制(如图10 左侧虚线线段)；系统高度位于小死区内或从小死区进入大死区后，不进行控制；从大死区外进入大死区，高度被控制到小死区范围内(如图10 右侧虚线线段)。可写成如下表达式：

图10 双死区设置的基本控制机理Fig. 10 Dual-deadband design in control

2.2 高度控制的滑模控制器设计

下面针对已建立的四分之一空气悬架系统进行滑模控制(sliding mode control, SMC)设计。考虑到控制的实现问题，对模型进行一定的简化[25]：1)视充放气过程中气室内气体很快达到均一状态，气室与外界近似视为绝热；2)假设车高调节中气室温度与大气温度近似相等。基于上述假设得到的四分之一悬架系统动力学状态方程可写为如下形式：

式(20)的详细表达式见附录2。借助微分几何中的Lie 导数运算方法，对上述非线性模型进行反馈线性化分析以便于控制理论的应用[16]。利用系统的动行程高度x1进行反馈控制，系统输出为：

分析系统的相对阶属性，可确定其相对阶为3，则反馈线性化后的系统整理为：

式中：

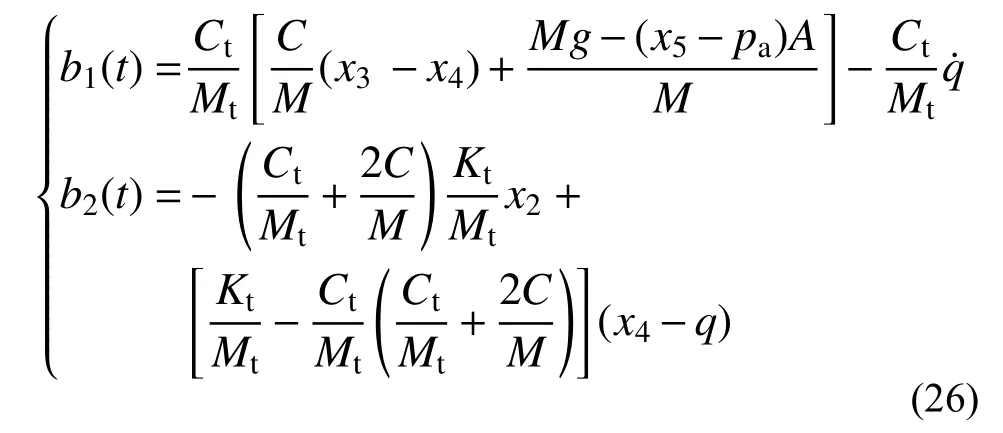
这两项对应了滑模面一阶导数中随机路面激励、非悬挂质量参数及位移等因素可能带来的扰动。假定这两部分分别满足有界条件：

式中，Ga为系统当前的质量流量。考虑到Gc表达式中存在无法测量的压强等参数，可以参考文献[25]进行压强观测器的设计，根据压强观测值pˆ1计算Gˆa。上述滑模控制器的设计可以充分发挥滑模控制在非线性控制领域的鲁棒性优势，对非悬挂部分参数变化、外界扰动等因素有着较强的抗干扰性。

3 系统仿真与验证

为验证上述四分之一空气悬架模型与控制策略的合理性，利用MATLAB/Simulink 仿真平台搭建了空气悬架的动力学模型，并进行了滑模高度控制器的设计。仿真工况包含：1)在系统处于静止状态下进行静态高度调节，设定车高变化20 mm为一挡，从初始高度依次完成升挡1 次、降挡2 次、再升挡1 次的控制操作；2)在系统行驶于C级路面时进行动态高度调节，设定车高变化30 mm为一挡，从初始高度依次完成升挡1 次、降挡2 次、再升挡1 次的控制操作。模型和控制参数见附录3，根据上述的模型控制器与仿真工况设计完成的仿真情况如图11、图12 所示。

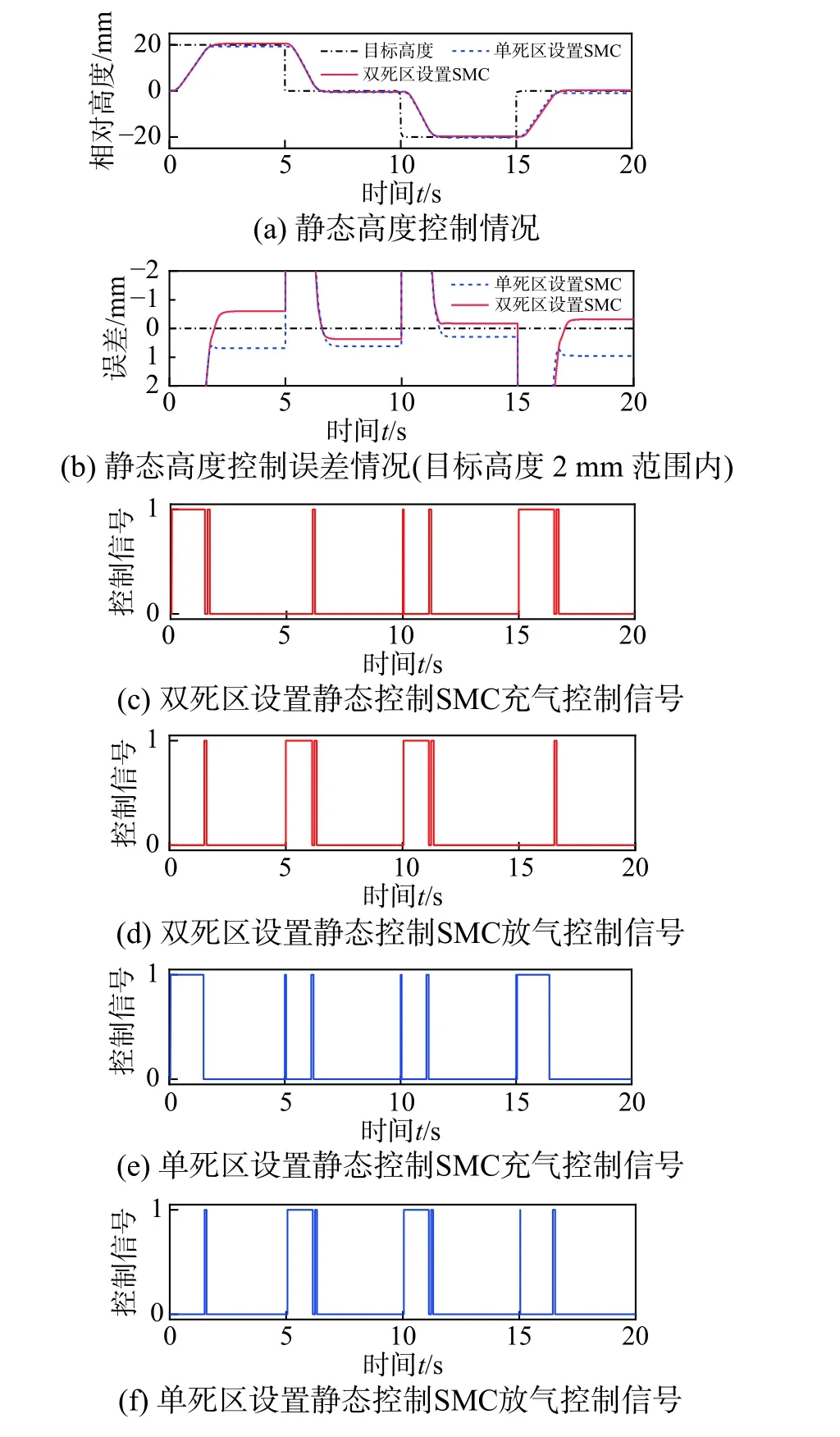
图11 静态高度控制的仿真情况Fig. 11 Simulation of static height control

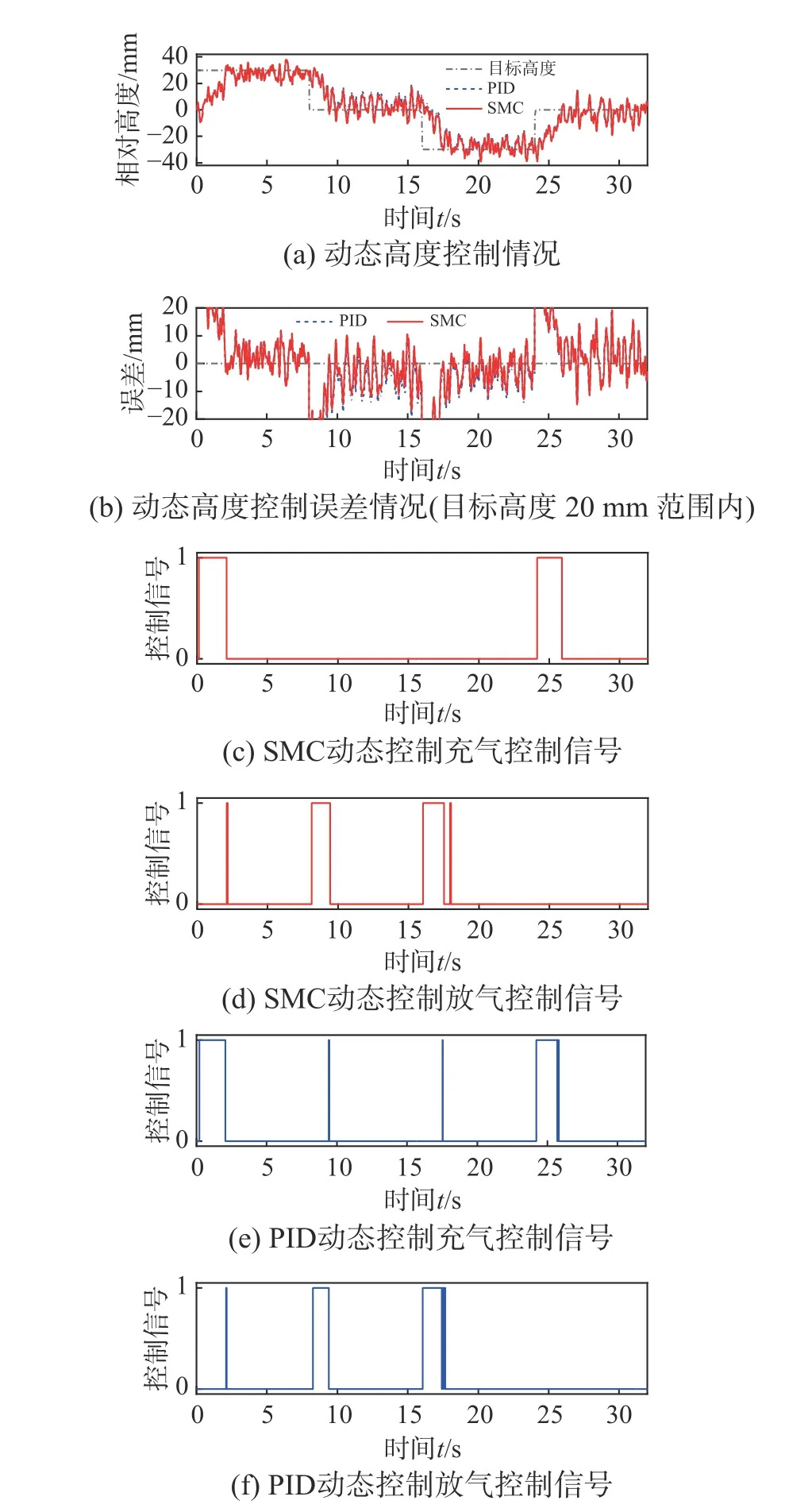
图12 动态高度控制的仿真情况Fig. 12 Simulation of dynamic height control

静态车高控制仿真中，对采用了双死区设置和单死区设置的滑模控制器(单死区范围与双死区的大死区范围相同)进行对比，2 种控制模式的稳态高度相对误差情况如图13 所示(计算方法见附录4)，图中箭头下方数字表示双死区设置相比于单死区设置的控制相对误差改善率。

图13 稳态高度相对误差(静态控制)Fig. 13 Relative errors of steady-state height (static control)

可见，不论采用单死区或双死区设置，本文提出的滑模控制策略都可有效实现静态车高控制，相比于设置的最大误差限10%(两种控制模式单边最大死区范围均为2 mm)，两种控制模式都能将高度误差控制在5%以内。其中双死区设置使得控制误差相比于单死区设置进一步改善10%以上。

动态车高控制仿真中，对采用双死区设置的PID 控制器与滑模控制器进行了对比，停止控制且车身平衡位置稳定后的高度误差均方根(root mean square error, RMSE)情况如图14 所示(计算方法见附录5)，图中箭头下方数字表示滑模控制器相比于PID 控制器的RMSE 改善率。可见，滑模控制方法相比于PID 控制方法的高度误差均方根值更小，控制精度有所提升。上述仿真过程验证了本文提出的双死区设置方法和滑模控制策略的有效性。

图14 车身平衡位置稳定后高度RMSE(动态控制)Fig. 14 RMSE of ride height when stabilized (dynamic control)

4 结论

本文提出一种基于热力学的空气悬架建模方法，并在此基础上提出了用于车高控制的双死区设置方法与有较好鲁棒性的滑模控制策略，完成了理论分析、实验对比及仿真验证的工作。主要结论如下：

(1) 建立的压强-温度双控制方程的空簧气室模型可以有效反映空气弹簧实际的非线性动力学特性。

(2) 提出的高度控制双死区设置方法可以减少外扰等因素造成的频繁控制模式切换，进一步提升控制精度。

(3) 提出的滑模车高控制策略在静态高度控制中有较高精度，动态高度控制精度较PID 控制更高。

本文的理论分析与仿真实验表明，所提出的空气悬架动力学模型能较好地反映实际工作特性，提出的双死区设置及滑模控制策略能够实现较高精度的空气悬架控制。

附录：

附录1. 较完备的空气悬架四分之一车辆动力学状态方程

附录2. 用于控制设计的四分之一车辆动力学状态方程

附录3. 仿真中采用的模型与控制参数见附表A1

表A1 参数表Table A1 Parameters

式中：N为该挡控制结束后车身平衡位置稳定时间段采样点个数；err(k)表示第k个采样点对应高度与目标高度的偏差。