羽流中固体颗粒在真空环境下分布的数值仿真①

李中华，李志辉，吴俊林，彭傲平

(中国空气动力研究与发展中心超高速所，绵阳 621000)

羽流中固体颗粒在真空环境下分布的数值仿真①

李中华，李志辉，吴俊林，彭傲平

(中国空气动力研究与发展中心超高速所，绵阳 621000)

通过对气-固两相间动量和能量相互作用解耦处理，建立了一种适于模拟真空环境气固两相混合物羽流的DSMC双向耦合算法与固体颗粒空间输运变化特性的TPMC计算技术。仿真了固体火箭发动机两相羽流流场和固体颗粒在远离发动机喷口数十公里空间扩散运动分布特性，通过将计算结果与典型文献结果及理论分析比较确认，证实本文方法的准确可靠性。结果表明，固体颗粒对气相的扩散有一定的阻滞作用;仅在离发动机喷口一定距离，气相对固体颗粒有较大影响，致颗粒温度下降、速度增加;颗粒温度随发动机喷口距离增大而减小，一直要在远离喷口上百公里颗粒温度才随轴向位置趋于平衡，且不同尺寸的颗粒温度差别较大，对指导外层空间高真空环境气固两相羽流传输影响工程研制具有重要意义。

稀薄气体;DSMC方法;两相流;双向耦合;TPMC方法;高空羽流

0 引言

固体火箭发动机广泛采用含金属复合推进剂，燃烧后会生成大量的固体颗粒。燃气射流通常是由多种气体成分、固体颗粒形成典型的两相多组分混合物流动，产生复杂的相互作用干扰流场［1－6］。如何准确可靠地模拟真空环境气固两相混合物羽流传输及固体颗粒远离喷口扩散运动轨迹、分布变化规律，一直是国内外学术界与工程应用部门关心的问题。

在高空，一般采用DSMC(Direct Simulation Monte Carlo)方法［7］模拟羽流流场。该方法采用有限数目的仿真分子模拟实际流场中数目巨大的真实分子。通过跟踪流场中仿真分子的运动和分子间的碰撞达到流场模拟的目的。该方法广泛用于模拟高空火箭或太空船推进器的羽流，在描述这些流动中的气体特性时有很高的精确度［8－9］。为了模拟气固两相流问题，Gallis提出了一种改进的DSMC模拟方案［10］，利用Green函数发展的DSMC方法适用于求解在任意分子速度分布的气相流场中颗粒所受的力和热，可模拟包括稀薄和化学惰性固体颗粒相在内的稀薄流动。但Gallis方法只考虑气相对固体颗粒的作用，忽略颗粒相作用于气体的影响。这种假定在固体推进剂火箭羽流中是有一定缺陷的，因为在固体火箭发动机羽流中，很多模拟范围内相间动量和能量的传递对气体流动特性有重大的影响。后来经Burt、Boyd等人的发展，建立了一种适用于DSMC方法的双向耦合(Two-way coupled)算法［5，11－13］，既考虑气相对固相的力和热的作用，又考虑固相颗粒对气相的作用，能较准确地描述固相颗粒在稀薄过渡流中的输运过程。

对于在大气层外真空环境工作的发动机，其羽流流场中含有大量Al2O3粒子，且大小不一。这些粒子会在空间形成一团粒子流云团，对相关的红外观测设备造成污染影响，而且粒子云团的存在还会严重干扰红外观测效果。对于长时间高真空环境工作的发动机，会出现羽流中固体颗粒如Al2O3粒子形成约数公里长的粒子流，随后又运动较长的时间。Al2O3粒子在数公里长的粒子流中的数密度、温度分布难以按照常规宏观流体力学数值方法和关于空间位置、速度的飞行力学数值推进计算确定。

为了研究大气层外高真空环境羽流场中固体颗粒空间分布、变化特性，本文在前期研究［9，14－16］基础上，提出发展适于气固两相羽流DSMC双向耦合算法与TPMC(Test Particle Monte Carlo)模拟技术，采用DSMC和TPMC相结合的方法开展研究，拟分两步进行计算。第一步，首先考虑发动机固定不动，把羽流视为一个定常问题，利用DSMC方法计算得到稳定喷流中流场温度、粒子数密度及粒子速度。在DSMC方法中，采用双向耦合算法计算固体颗粒与喷流气体分子之间的相互作用。第二步，在第一步计算的基础上，分析得到发动机喷流径向剖面上的流场温度、粒子数密度及粒子速度基本不再受喷流气体影响的剖面计算参数(包括粒子数密度、温度、流动速度)，以此数据为基础，采用TPMC方法计算粒子在远离发动机喷口的空间位置分布，得到不同时刻粒子的温度和数密度分布。

1 气-固两相羽流DSMC双向耦合算法

DSMC方法是羽流流场计算行之有效的模拟方法。依托DSMC方法，采用变刚球分子模型，能量交换使用Larsen-Borgnakke模型［17］;网格采用二级直角网格，碰撞网格根据密度自适应［9，14－15］，碰撞对的选取限制在碰撞网格内，发展考虑气-固两相相互作用影响的DSMC双向耦合算法。为了提高计算效率，采用了基于MPI的DSMC并行计算技术，将计算区域分解为N个子区域，分别分配给N个节点。各节点进行独立且完整的DSMC仿真。仿真分子穿过边界区域时，计算区域之间进行仿真数据信息交换。两相流DSMC模拟运算准则是基于相间动量和能量从微粒特性的瞬时变化的传递进行解耦，分为两个方面:

(1)考虑气相对固体颗粒的作用［10］。假设固体颗粒处于当地自由分子流的状态，不考虑多原子气体的振动激发，在同一个网格里气相的每个DSMC仿真分子作用到一个固体颗粒上的能量和动量可表示为

式中 Rp为等效颗粒半径;Ng为每个仿真分子所模拟的真实气体分子数目;τ为颗粒表面热适应系数;Vc为网格体积;m为单个气体分子质量;ur为气体分子与相关颗粒的相对速度，cr是ur的绝对值;k为Boltzmann常数;Tp为颗粒温度;Λ为气体转动自由度数;erot为单个分子转动能。

(2)考虑固体颗粒对周围气体的影响，首先要确定在每个时间步长内哪个仿真分子将与颗粒进行碰撞。通过对Bird的非时间计数方法［7］进行修正，来确定与所选的颗粒可能发生碰撞的仿真分子数ns。

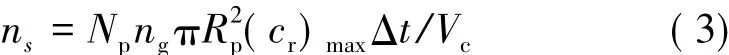
式中 Np为一个仿真颗粒所表示的实际固体颗粒数量;ng为与固体颗粒在同一网格里的气体仿真分子数;Δt为时间步长;(cr)max为网格内采样到的分子-颗粒对碰撞前最大相对速度。

一个与这个颗粒发生碰撞的给定的气体仿真分子，要么为以概率等于颗粒热适应系数τ的等温漫反射碰撞，要么为概率为1-τ的镜面反射。如果发生镜面反射，则相对速度cr在碰撞中不发生改变，碰撞后的相对速度可通过cr与单位矢量⇀n相乘得到。如果发生漫反射，碰撞后相对速度围绕初始相对速度的方位角ε在［0，2π］上等概率分布。在漫反射碰撞中，碰撞后相对速度能假定为等于初始相对速度cr，而是需要通过使用“取舍”法，从如下分布函数来确定的值:

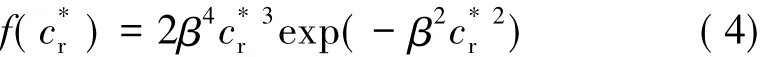
式中 β为气体基于颗粒温度的最可几热运动速度的倒数，β=［m/(2kTp)］1/2。

2 真空环境固体颗粒分布TPMC计算

大气层外真空环境发动机长时间工作，固体颗粒会随羽流扩散运动到离发动机喷口很远的距离，这时再采用上文介绍的DSMC和双向耦合算法来模拟颗粒运动分布，显然不再合适。为了跟踪固体颗粒长时间的运动轨迹，本文建立了一种粒子跟踪的TPMC方法。发动机羽流在真空环境膨胀到一定程度后，流场中气流密度会变得很低，气相和固相不再相互作用。这时，固体颗粒保持匀速直线运动。在这样的羽流场，模拟固体颗粒的TPMC方法基本步骤可设计为

(1)在羽流场入口处产生一个样本粒子(试验粒子)。根据DSMC方法得到羽流场的结果，在TPMC界面上随机产生一个固体颗粒。

(2)跟踪颗粒的运动。颗粒在起始点以本身所具有的速度做匀速直线运动。在给定时间步长内，运动到新的位置。运动一定时间后，记录颗粒的位置。

(3)在大气层外真空环境中运动，固体颗粒要吸收太阳辐射能量，本身也要向外辐射能量，温度会发生变化，要进行温度变化的处理。

(4)重复(1)～(3)的过程，直到记录到足够多颗粒为止。

还需要建立在高真空环境考虑太阳辐射影响的可计算模型。假设太阳辐射是均匀的，单位时间固体颗粒受到太阳辐射的能量为

式中 Es为固体颗粒受到的太阳辐射能量功率;fa为太阳常数;在外层空间高真空环境可设置fa=1 368 W/m2;Sp为颗粒等效受热面积;α为发射系数和吸收系数。

在Δt时间步长内，颗粒受太阳辐射引起的温度变化可表示为

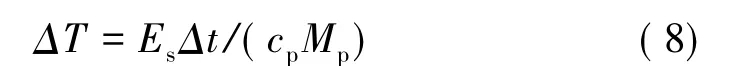
式中 cp为颗粒材料的比重压热容;Mp为颗粒质量。

颗粒由自身辐射引起的温度变化应为

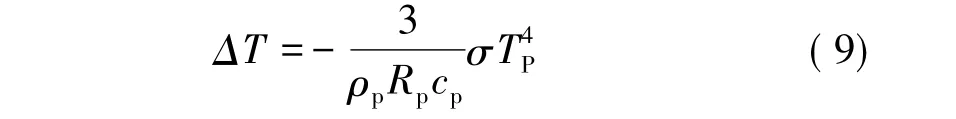
式中 σ为Stefan-Boltzmann常数;cp为颗粒材料的热容;ρp为颗粒材料密度。

在每个时间步长内，对式(8)和式(9)进行迭代求解，可给出颗粒的温度变化。

颗粒数分布按颗粒半径的连续分布密度，可近似地由对数正态分布曲线来拟合［18］。即

3 算例与结果讨论

3.1 气-固相互作用模型验证

为了比较确认本文发展的两相流双向耦合算法的准确可靠性，基于文献［11］提供两相稀薄流中一个气-固相互作用影响模拟的双向耦合模型算例，拟定0.1 mm宽和20 mm长的矩形区域(图1)进行计算。

模拟中，气相混合物为H2、CO和N2组成的混合气体，分子数密度分别设置为 2×1023、1×1023、1×1023m－3;在入口处，气体速度为2 000 m/s，温度为1 000 K。固相有2 种铝粒子:直径分别为 3×10－6、6×10－6m，每种粒子的质量流量相等;在入口边界上，粒子的速度为1 200 m/s，温度为 2 200 K。

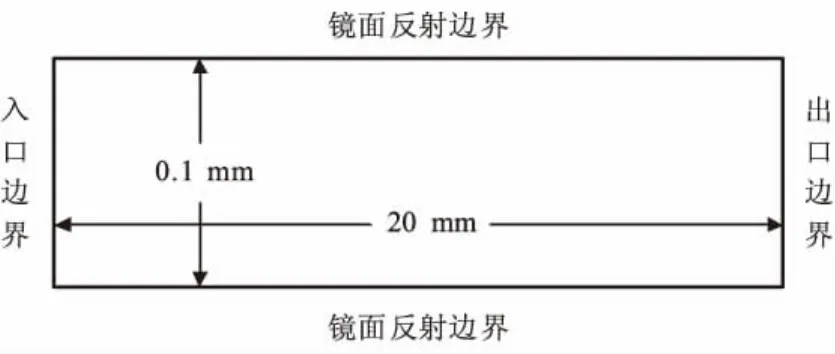
图1 气固两相流计算区域与边界条件示意图Fig.1 Sketch of domain and boundary types

图2和图3绘出了流场中不同截面上动量与能量传递速率随位置的变化关系。图中显示，气-固两相之间有较强的动量和能量传递。

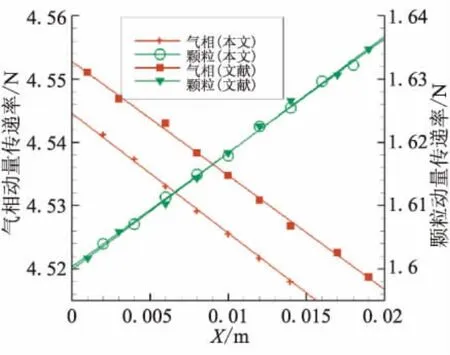
图2 两相流中动量传递速率随位置变化比较Fig.2 Comparison of momentum transfer rates

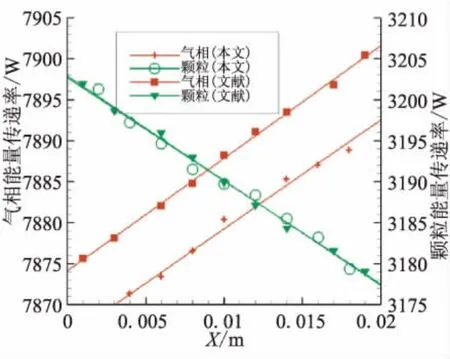
图3 两相流中能量传递速率随位置变化比较Fig.3 Comparison of energy transfer rates

通过比较气相和固相的变化梯度，可看出两者的梯度大小大致相等，符号相反。这表明在模拟计算中，气相作用在固相的动量和能量，等于固相反作用于气相的动量和能量，即在相间相互作用时，动量和能量是守恒的。在前面介绍的双向耦合算法中，气相对固相的作用和固相对气相的作用过程是解耦的，两个过程独立计算。在计算固相对气相的作用时，其过程是一个随机统计计算过程，不能保证在每一步的计算中严格地遵守动量和能量守恒，但在大样本数情况下统计平均时，可保证动量和能量守恒。通过图2、图3将本文仿真模拟方法结果与典型文献结果［11］进行定量化对比分析，表明本文所建立的气-固两相流动DSMC双向耦合算法用于计算仿真固体火箭发动机羽流中气相混合物与固体颗粒输运过程是可靠的。

3.2 固体发动机两相羽流流场计算

本文对某固体发动机真空环境产生的两相羽流流场进行模拟，其中发动机出口马赫数1.5，出口温度2 960 K，出口速度设为均匀流动，固体颗粒的质量流量占总流量的30%。羽流中气相组元的摩尔分数见表1。

表1 羽流气相组元摩尔分数Table 1 Mole fraction of plume gas species

计算中，背景环境设为真空边界条件。关于固体颗粒Al2O3的模拟，采用有限分组方法，根据式(10)，把Al2O3分成不同尺寸和质量的5组，视为5种颗粒来处理。每一组颗粒具有相同的尺寸和质量，颗粒直径在20～200 μm之间，具体尺寸见表2。

表2 固体颗粒尺寸Table 2 Particles size

图4给出了计算得到的两相羽流流场数密度分布等值线云图。从图4(a)的气相流场可看出，由于喷流出口马赫数较低，只比音速稍高，喷流向真空膨胀十分迅速。沿流动方向，数密度迅速下降，温度下降也很快。沿径向，数密度下降更快。固相颗粒的扩散是气相扩散引起的，图4(b)中，显示出固相颗粒的扩散是有界的。当气相膨胀到密度很低时，对固相颗粒的影响会变得很小，颗粒会保持自己的运动状态做匀速直线运动。从数密度分布来看，固体颗粒比较集中地分布在核心区域。为了验证固体颗粒对气相羽流的影响，还进行了不包含固体颗粒的单相羽流对比计算。图5给出了考虑固体颗粒对气相影响的两相羽流与单相羽流2种情况下模拟得到的羽流轴线上气相温度与流动速度分布比较。可看出，单相羽流模拟得到的气体流动速度较双相羽流模拟值普遍偏大，说明在没有固体颗粒的情况下，气相流场膨胀得更快，速度增加更多，在x－=6处(以喷流半径为参考无量纲化)2种情况模拟得到的速度相差约160 m/s，证实固体颗粒对气相的扩散有一定的阻滞作用。两相情况下，气体不断从颗粒相吸收能量，温度较高，图中显示出在x－=6处，两相羽流模拟得到的气相温度高于单相羽流模拟值约40 K。

图6给出了该发动机两相羽流场中固体颗粒温度分布等值线云图，呈现出复杂流场结构，沿轴向，随着气相的迅速膨胀，温度迅速下降，能量从固体颗粒向气相转化，颗粒的温度也逐渐下降。沿径向，轴线附近颗粒的温度比外围的温度稍低，更外围的颗粒温度更低，这是因为表2设置的5种颗粒与气相相互作用时能量交换不同，导致颗粒的温度不同;同时，动量交换也不相同，颗粒扩散的程度因此会有所差异，这些因素导致温度的分布比较复杂。不过整个流场中颗粒温度分布差别不大，最大差异在300 K左右。由图7所示的颗粒轴向速度分布表明，外围颗粒被气相加速较大，这是因为外围主要是小尺寸的颗粒，颗粒尺寸越小，越容易被气相加速。

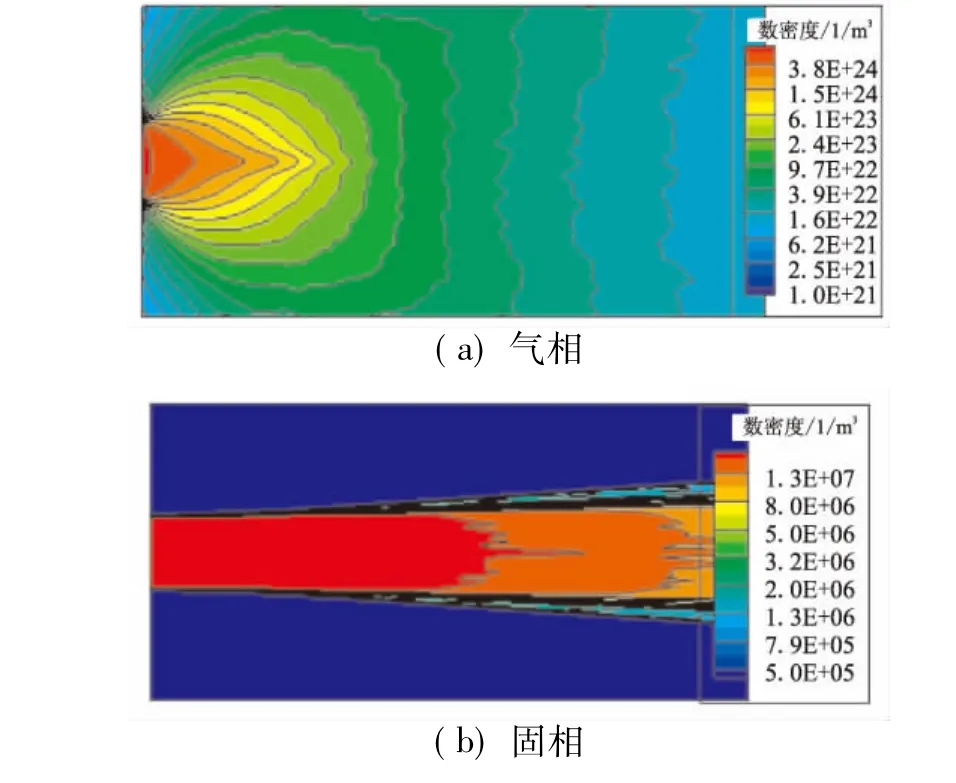
图4 两相羽流流场数密度分布Fig.4 Number density distribution in two-phase plume flow field

图5 单相和两相羽流轴线上温度与流动速度分布比较Fig.5 Comparison on temperature and flow velocity distribution of one-and two-phase plume flows

图6 羽流中固体颗粒温度分布Fig.6 Particles temperature distribution in two-phase plume flow field

图7给出5种颗粒沿羽流轴线不同位置的温度、速度分布，显示出在距离喷口x－=5以内的羽流场中，气相对固体颗粒有较大影响，颗粒温度下降和速度增加较快，由此计算证实了式(1)、式(2)表征的气相分子数对固相颗粒动量和能量的作用影响很大;但在x－=5处，气相数密度比出口处下降1个量级，此时气相对固体颗粒的影响已经变得很小。x－＞5之后，不同位置的颗粒温度下降和速度增加较小，基本上各种颗粒的温度、速度分布均保持在相应量值。

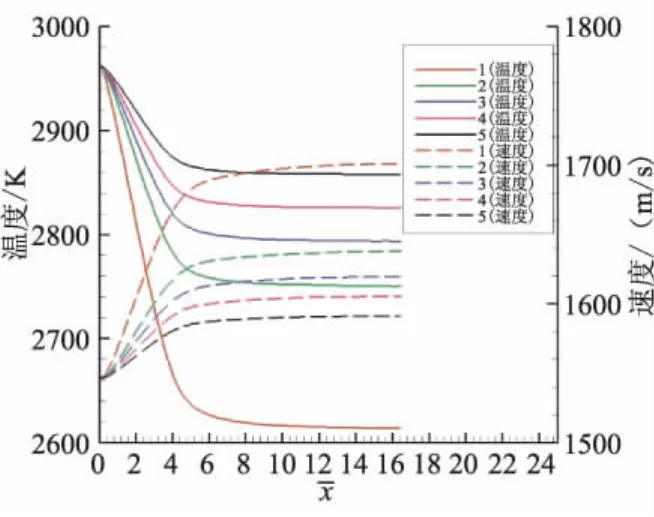
图7 不同固体颗粒沿轴线温度、速度分布计算比较Fig.7 Comparison on temperature and velocity distribution of particles along the axis of the plume flow

为了揭示该发动机长时间真空环境工作所产生两相羽流场固体颗粒运动轨迹与分布特性，利用所建立TPMC方法，对发动机工作70 s后的颗粒分布进行了模拟计算。由于考虑太阳辐射和自身辐射时，发射系数对颗粒温度变化过程有一定影响。根据文献［19］中的结果，Al2O3在 800～1 300 K 之间、波长为 1.89 μm的发射系数比较接近0.5，而且随温度变化不大。因此，在计算中假设，Al2O3在所有温度范围、各波段内的发射系数均为0.5。图8给出了发动机工作70 s后，第1种颗粒在中心对称面的数密度、温度等值线云图分布。计算表明，此时在羽流轴线方向，粒子扩散到离发动机喷口63～115 km范围的扇形区域内。在周向，基本上保持轴对称分布，由此颗粒分布是在一个近似圆台的范围内，扩散范围很大。图9展示了本文计算设置的5种颗粒分别在离发动机喷口74、115 km的扩散半径(R)与颗粒直径(dp)变化关系。由图9分析，颗粒直径越大，扩散半径越小，两者基本上呈反比关系。

图10绘出了该发动机羽流轴对称中心线上不同颗粒的温度随远离喷口轴向位置60 km＜x＜110 km变化关系。图10中显示出，颗粒温度随远离喷口位置增大而减小;颗粒尺寸越大，起始温度越高，在整个扩散过程中，也保持较高的温度。在发动机工作达70 s时，尺寸最小的第1种颗粒温度随位置x基本保持不变而趋近平衡温度，其他颗粒仍随轴向位置x增大而减小，还未到达平衡温度。这种现象说明，受太阳辐射和自身辐射的影响，颗粒温度随着远离发动机喷口的扩散运动而逐渐下降，一直要在远离发动机喷口上百公里颗粒温度，才随轴向位置x逐渐趋于平衡，且不同尺寸的颗粒温度也各不相同。这对指导固体发动机高真空环境气固两相羽流空间环境影响工程研制具有重要意义。

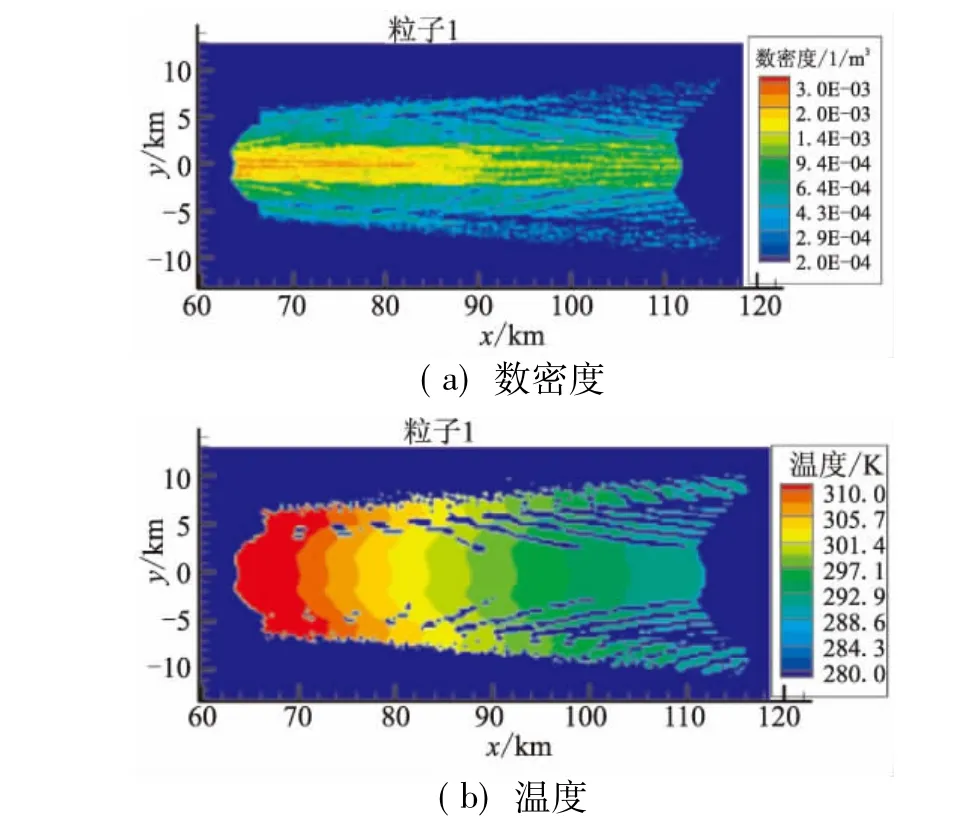
图8 发动机工作70 s后颗粒1参数分布Fig.8 Number density and temperature distribution for Particle 1 after 70 s with engine working

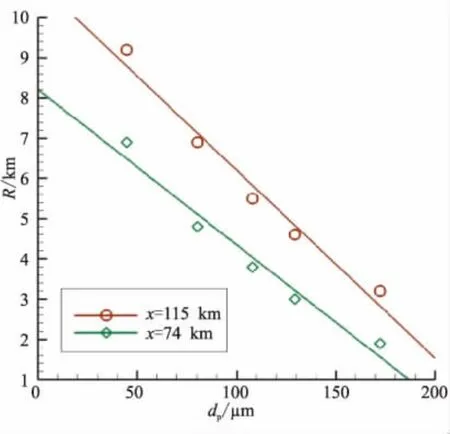
图9 颗粒扩散半径与颗粒直径的关系Fig.9 Relation between diffused radius and particle diameters

图10 不同颗粒温度分布比较Fig.10 Comparison on temperature distribution for different types of particles

4 结论

(1)采用双向耦合技术，建立了适于气固两相多组元混合物羽流问题DSMC仿真方法，通过对相间相互作用进行解耦处理，实现了气-固两相间动量和能量相互作用的模拟。研究证实固体颗粒对气相的扩散有一定的阻滞作用，会使气相温度增加。颗粒温度下降，且沿径向轴线附近颗粒温度比外围温度稍低。

(2)在距离发动机喷口一定位置，如x－=5以内的羽流场中，气相对固体颗粒有较大影响，颗粒温度下降和速度增加，而在x－＞5之后不同位置，气相对固体颗粒的影响甚微，颗粒温度和速度逐渐趋于相应平衡值。

(3)研制了一套适于真空环境固体颗粒空间分布运动特性模拟的TPMC方法。通过对发动机长时间工作(如70 s)所产生颗粒分布进行模拟计算，结果表明，颗粒扩散集聚到离发动机喷口63～115 km范围的近似圆台区域;在一定气体数密度范围内，羽流中气-固两相有较强的相互作用，颗粒尺寸对颗粒的扩散范围和温度分布有很大影响。颗粒直径越大，扩散半径越小，两者基本上呈反比关系。

(4)受太阳辐射和自身辐射的影响，颗粒温度随着远离发动机喷口的扩散运动而逐渐下降，直至远离发动机喷口上百公里颗粒温度，才随轴向位置逐渐趋于平衡，且不同尺寸的颗粒温度也各不相同。对指导固体发动机高真空环境气固两相羽流空间环境影响工程研制具有重要作用。

(5)通过DSMC和TPMC方法相结合，本文方法为稀薄两相流的计算、大尺度范围内计算高空羽流中颗粒输运过程提供了一种数值模拟手段。研究体会到，固体颗粒尺寸对颗粒的扩散范围和温度分布有很大影响。在一定气体数密度范围内，羽流中气-固两相有较强的相互作用。在气体数密度很小时，气-固两相作用很弱，可不予考虑。

［1］Dettleff G.Plume flow and plume impingement in space technology［J］.Progress in Aerospace Sciences，1991，28(1).

［2］Siebenhaar A，Bulman M J.The strutjet engine:the overlooked option for space launch［R］.AIAA 95-3124.

［3］于胜春，汤龙生.固体火箭发动机喷管及羽流流场的数值分析［J］.固体火箭技术，2004，27(2).

［4］李东霞，徐旭，蔡国飙，等.火箭发动机气体-颗粒两相流双流体模型研究［J］.固体火箭技术，2005，28(4).

［5］Marris H，Deboudt K，Augustin P，et al.Fast changes in chemical composition and size distribution of fine particles during the near-field transport of industrial plumes［J］.Science of The Total Environment，2012，427-428:126-138.

［6］Johnson G R，Jayaratne E R，Lau J，et al.Remote measurement of diesel locomotive emission factors and particle size distributions［J］.Atmospheric Environment，2013，81:148-157.

［7］Bird G A.Molecular gas dynamics and the direct simulation of gas flows［M］.London:Oxford Univ.Press，1994.

［8］Ivanov M S，Khotyanovskyy D V，Kudryavtsev A N，et al.Numerical study of backflow for nozzle plumes expanding into Vacuum［R］.AIAA 2004-2687.

［9］李志辉，李中华，杨东升，等.卫星姿控发动机混合物羽流场分区耦合计算研究［J］.空气动力学学报，2012，30(4):483-491.

［10］Gallis M A，Rader D J，Torczynski J R.DSMC simulations of the thermophoretic force on a spherical macroscopic particle［R］.AIAA 2001-2890，American Institute of Aeronautics and Astronautics，Washington，D C，2001.

［11］Burt J M，Boyd I D.Development of a two-way coupled model for two phase rarefied flows［C］//42nd AIAA Aerospace Sciences Meeting and Exhibit，Reno，Nevada，5-8 Jan.2004，AIAA 2004-1351.

［12］Burt J M，Boyd I D.Monte carlo simulation of a rarefied multiphase plume flow［C］//43rd AIAA Aerospace Sciences Meeting and Exhibit 10-13 January 2005，Reno，Nevada.2005，AIAA 2005-964.

［13］Harris A J L，Ripepe M，Hughes E A.Detailed analysis of particle launch velocities，size distributions and gas densities during normal explosions at Stromboli［J］.Journal of Volcanology and Geothermal Research，2012，231-232:109-131.

［14］李中华.飞行器材料高空放气污染蒙特卡罗数值模拟［C］//中国宇航学会首届学术年会，2005.

［15］李中华，李志辉，李海燕，等.过渡流区NS/DSMC耦合算法研究［J］.空气动力学学报，2013，31(3).

［16］Li Z H，Wu J L，Peng A P.Coupled navier-stokes/direct simulation monte carlo simulation of multicomponent mixture plume flows［J］.Journal of Propulsion and Power，2014，30(3):672-689.

［17］Borgnakke C，Larsen P S.Statistical collision model for Monte Carlo simulation of polyatomic gas mixtures［J］.J.of Comput.Phys.，1975，18:405-420.

［18］李洁，任兵，陈伟芳.稀薄流过渡区气固两相喷流的建模与数值模拟［J］.空气动力学学报，2005，23(4).

［19］Freeman G N，Ludwing C B，Malkmus W，et al.Development and validation of standardized infrared radiation model(SIRRM)［R］.AFRPL 79-55.

(编辑:崔贤彬)

Numerical simulation on particle distribution of the plume flow in vacuum

LI Zhong-hua，LI Zhi-hui，WU Jun-lin，PENG Ao-ping
(China Aerodynamics Research and Development Center，Mianyang 621000，China)

A numerical simulation approach was presented to simulate rarefied two-phase mixture plume flow by applying twoway coupling technique of DSMC method.The interaction between rarefied gas and solid particles was dealt with decoupling computation of momentum and energy exchange between phases.The TPMC computing technology was also developed to solve the space transport characteristics of solid particles in distant field space.The two-phase plume flow field and particle distribution characteristics far away from the engine nozzle were simulated by the DSMC and TPMC method.It is indicated that the present methods and models are correct by the comparison of the computed results with the typical confirmed results from the reference and theoretical analysis.There exists some retarded elasticity in gas phase diffusion of solid particles to some extent.From the engine nozzle distance，gas and solid particles have a greater impact caused with temperature drop and increases of the speed of particles.The granular temperature away from the nozzle exit tends to balance，and the particle temperature is very different with different size of particles.It is shown that there are more intensely interaction between phases in case of higher number density，and particle size affects diffusing range and temperature distribution.The results are of great significance to guide the vacuum gas-solid two-phase plume transmission.

rarefied gas;DSMC method;two-phase flow;two-way coupled method;TPMC method;plume flow

V438

A

1006-2793(2014)06-0797-07

10.7673/j.issn.1006-2793.2014.06.011

2014-03-03;

2014-08-12。

973计划(2014CB744100);国家自然科学基金(91016027、11325212);国防基础科研基金(51313030104)。

李中华(1970—)，男，高工，研究方向为稀薄气体动力学。E-mail:lzhzcb@aliyun.com

李志辉。E-mail:zhli0097@x263.net