求解非负约束优化问题的可行LS共轭梯度法*
刘陶文,周 蓉
( 湖南大学 数学与计量经济学院,湖南 长沙 410082 )
非负约束优化问题广泛存在于许多学科及工程应用领域中,如:非线性回归分析、金融投资、大地测量、卫星导航等,并且有关的数据处理是非常庞大的,呈现的问题通常是大规模的.因此,研究求解这些问题的高效算法具有重要的现实意义.非负约束优化问题的一般形式为

(1)
这里函数f:Rn→R是连续可微的,D={x∈Rn:x≥0}是可行域.
问题(1)的一阶最优性条件 ( KKT条件 )可以表示为

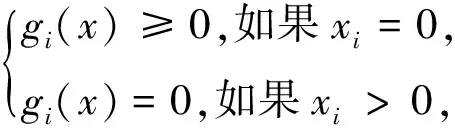
(2)
这里g(x)=▽f(x)表示函数f在点x处的梯度,gi(x)表示g(x)的第i个分量.满足条件(2)的点x被称为问题(1)的一个KKT点.
与问题(1)相关的是下面的有界约束问题:

(3)
这里l和u是Rn中的有界向量.许多研究集中于求解大规模有界约束问题(3),人们提出了如谱梯度投影法、有限记忆拟牛顿法和共轭梯度法等有效算法[1,4,6].尽管问题(1)可以看作问题(3)的特殊情形,但不知这些方法能否经过适当的修改被用来求解非负约束问题.
众所周知,共轭梯度法及其修正形式是求解大规模无约束问题minf(x),x∈Rn的有效方法[2,7-8].因此,人们设想用共轭梯度法的思想求解约束问题.文献[6]研究了用共轭梯度的思想求解有界约束问题(3),通过求解一个约束子问题来计算搜索方向,作者证明了在 Wolfe型线性搜索下所提出的方法是收敛的.然而已有研究表明在该研究上存在许多的困难[5].
在本文中,我们研究用共轭梯度型方法求解非负约束问题 (1).结合已有求解有界约束问题的子空间思想[4]和求解无约束问题的Liu-Storey (LS)共轭梯度法[3],提出了一个求解问题(1)的可行LS共轭梯度法,与文献[6]的方法比较,本文提出的方法的优点是无需求解子问题,并且在Armijo搜索下具有全局收敛性,节省大量计算.
1 计算下降可行方向
给定x∈D及常数ε>0,首先定义如下的索引集合:
B(x)={i:xi>ε},
A1(x)={i:xi=0,gi(x)≥0}∪{i:0 A2(x)={i:0≤xi≤ε,gi(x)<0}, A3(x)={i:0 (4) 我们称集合A(x)=A1(x)∪A2(x)∪A3(x)为x处的有效集,而B(x)称为非有效集. 设xk∈D是问题(1)的一个近似解,为了计算在该点处的下降可行搜索方向dk∈Rn,采用如下策略:由于A1(xk)中的变量满足条件(2),这些变量的取值保持不变; 对于A3(xk)中的变量,由于-gi(xk)指向可行域的边界,对-gi(xk)进行截断处理获得搜索方向;对于B(xk)∪A2(xk)中的变量先计算某种共轭梯度型方向,然后进行适当的截断处理产生搜索方向.dk的具体计算方法如下: 设矩阵Pk由列{ei:i∈B(xk)∪A2(xk)}构成,矩阵Qk由列{ek:i∈A3(xk)}构成,其中ei表示n阶单位矩阵的第i列.首先计算共轭梯度方向如下: (5) 这里gk=g(xk),yk=gk-gk-1,并且 (6) 容易验证 令 (7) (8) (9) 因此,由dk的定义(7)可得 (10) 证毕 证由KKT条件(2)以及(10)即可验证定理结论成立. 证毕 现在提出求解问题(1)的可行LS共轭梯度算法如下: 算法1(可行LS共轭梯度法) 步 0:取初始点x0∈D,常数ρ,σ∈(0,1),ε>0.令k=0. 加拿大林间猫头鹰的鸣声“呵呵——呵——呵——”,极像老翁冷冷的笑声,与我记忆中江南的猫头鹰的叫法“骨碌碌碌……”圆滚而阴森的鸣音,大异其趣。鸱鸮的鸣法会超过人类的方言上万种吗?鸟啼人语,都是天趣。 f(xk+αdk)≤f(xk)-σ‖αdk‖2 (11) 的最大值αk.令xk+1=xk+αkdk. 步4:令k:=k+1,然后转步1. 在算法1的步3中,使用了Armijo 型线性搜索(11)计算步长αk,这比文献[6]中使用的Wolfe 型搜索更容易实现,而且节省大量投影计算.显然由算法1产生的序列{xk}⊂D. 下面分析算法1的全局收敛性.首先作如下的假设: 假设A由算法1产生的序列{xk}在D内是有界的,函数f(x)在D内有下界并且其梯度g(x)在可行域D内是Lipschitz连续的,即存在常数L>0满足 ‖g(x)-g(y)‖ ≤L‖x-y‖,∀x,y∈D. 注当dk≠0,dk是f(x)在xk处的一个下降可行方向,从而由假设A可知序列{f(xk)}单调下降且有下界,从而得到 (12) (13) 证根据索引分类(4)分4种情形进行讨论. 情形1:当i∈B(xk)时,(xk)i>ε,故 情形2:当i∈A1(xk)时,(xk)i+γ(dk)i=0,∀γ≥0. 情形3:当i∈A2(xk)时, 情形4:当i∈A3(xk)时,gi(xk)≥0,即有 以上的讨论表明(13)成立. 证毕 引理3如果存在某个常数δ>0使得 那么序列{dk}是有界的,即存在常数M>0使得‖dk‖∞≤M. 证在假设A的条件下,{xk},{gk}是有界的,即存在常数M1>0,使得 ‖xk‖∞≤M1,‖gk‖∞≤M1,∀k≥0. (14) 另一方面,由(12),必存在常数μ∈(0,1)及正整数k1,使得 2δ-1M1L‖αk-1dk-1‖ ≤μ,∀k≥k1. 因此,∀k≥k1,进一步有 所以,对任意的k≥0,有 证毕 利用引理3,可以得到下面的全局收敛性定理. 定理2设序列{xk}由算法1产生.如果假设A 成立,则有 (15) 下面对步长αk分两种情形讨论. 另一方面,由泰勒中值定理及g(x)的 Lipschitz 连续性容易验证 由上面的两个不等式可推出 证毕 由定理1及定理2知,必存在迭代序列{xk}的某一个极限点x*是问题 (1)的KKT点. 在这一节,将所提出的算法应用于大地测量中数据处理问题[9].对一理想边坡因地质断层构成一可能的滑体,按地质学知识,滑体只能沿底盘向东北方向偏下移动.选定三个基点,其坐标分别为A(500.00,0,100.00),B(0.00,-500.00,150.00),C(500.00,500.00,200.00).在滑体上,取监测点P(0,0,100.00),分别在基点A,B,C处用边前方交会监测P点的位移(x,y,-z),AP,BP和CP为3个观测边,且有先验信息x,y,z>0.设观测向量为L∈R3,则有相应的误差方程: L+V=(|AP|,|BP|,|CP|)T, 其中V为观察噪声向量.设A,B,C3个边观测的一次观测值分别为500.04,502.52,714.13.试估计P点的位移(x,y,-z). 当P点有位移(x,y,-z)时,观测向量L的误差方程为: 文献[9]将误差方程线性化后,利用求解线性互补问题的Lemke算法求解得P点位移的最小二乘估计.由于线性化产生的误差及Lemke算法的计算复杂性,这种估计的精度是有限的. 记函数. 则P点位移的估计问题等价于下面的带非负约束的非线性最小二乘问题: (16) [1]BIRGIN E G,MARTINEZ J M,RAYDAN M.Non-monotone spectral projection gradient methods on convex sets [J].SIAM Journal on Optimization,2000,10(1):1196-1211. [2]DAI Y,YUAN Y.Nonlinear conjugate gradient methods [M].Shanghai:Shanghai Science and Technology Publisher,2000. [3]LIU Y,STOREY C.Efficient generated conjugate gradient algorithms Part 1:Theory [J].Journal of Optimization Theory and Applications,1991,69(1):129-137. [4]NI Q,YUAN Y.A subspace limited memory quasi-Newton algorithm for large-scale nonlinear bound constrained optimization [J].Mathematics of Computation,1997,66(220):1509-1520. [5]NOCEDAL J.Conjugate gradient methods and nonlinear optimization,In:Linear and nonlinear conjugate gradient-Related method [M].Philadelphia,SIAM Press,1996,9-23. [6]PYTLAK R.An efficient algorithmfor large-scale nonlinear programming problems with simple bounds on the variables [J].SIAM Journal on Optimization,1998,8(2):532-560. [7]ZHANG L,ZHOU W J,LI D H.A descent modified Polak-Rebière-Polyak conjugate gradient method and its global convergence [J].IMA Journal of Numerical Analysis,2006,26(4):629-640. [8]ZHANG L,JIAN S Y.Further studies on the Wei-Yao-Liu nonlinear conjugate gradient method [J].Applied Mathematics and Computation,2013,219 (14):7616-7621. [9]宋迎春,朱建军,罗德仁,等.附非负约束平差模型的最小二乘估计 [J].武汉大学学报:信息科学版,2008,33(9):907-909. SONG Ying-cun,ZHU Jian-jun,LUO De-ren,etal.Least-squares estimation of nonnegative constrained adjustment model [J].Geomatics and Information Science of Wuhan University:Information and Science,2008,33(9):907-909 .(In Chinese)
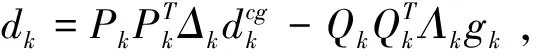






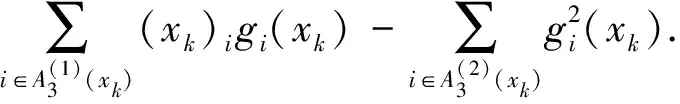




2 算法结构及其收敛性分析


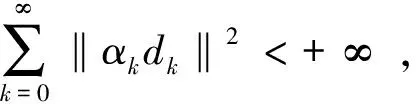


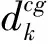

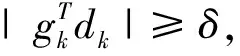



3 数值实验




