借助几何图形理解高等数学中的抽象概念和结论

赵小艳， 李换琴

(西安交通大学数学与统计学院，陕西西安710049)

当代科学技术的发展对数学知识的需求越来越深、越来越广、越来越现代化，而高等数学是大学生进入大学必修的第一门数学基础课，它对学生关于数学概念的理解和对数学思想和所学内容的可应用性的掌握以及数学思维的培养起着至关重要的作用.然而，我国国内的高等数学教材内容是比较抽象的.学生普遍认为“高等数学是神圣的、高高在上的”，也是“望而生畏”的，很难主动的带着兴趣去学习. 因此，如何帮助学生直观、形象的理解高等数学中的概念和结论，是教师在教学中的一个重点和难点.考虑到几何图形简单直观，如果能将高等数学的一些概念和结论与几何图形紧密的结合，必有助于加深学生对抽象数学概念结论的理解，激发学生的兴趣.国家教育发展纲要[1]中指出：“……(四)探索多样化人才培养新模式……，探索学生自主学习模式, 创新教育教学方法，开展启发式、探究式、讨论式、参与式教学，……”.如果能在教学中让学生主动思考、动手去做，一方面加深学生对这些概念结论的理解，另一方面，亦可提高学生的计算机能力，培养学生的数学思想.本文通过几个具体案例说明这个问题.

1 用几何图形从两个方面加深对重要极限的理解

图1 函数f(x)=sinx/x的图形 图2 函数y=sinx和y=x的图形

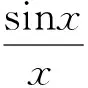
2 利用图形理解微分概念

在讲函数的微分时，传统的教学方式是通过例子给出微分的定义，讨论导数与微分的关系得出微分的表达式，后面就关注于微分的计算及应用，比如突出微分形式的不变性等.学生对于微分的理解不够透彻，不能理解dx与dy的真正意义.微分是微分学转向积分学的一个关键概念.绘制微分的几何图形有助于直观的理解微分思想.事实上，微分的思想就是线性近似计算，即在局部范围，用线性函数近似代替非线性函数.下面通过一个例子说明.

设f(x)=x3,一阶导数为f′(x)=3x2,函数f(x)在x=1处的切线为

y=f(1)+f′(1)(x-1)=3x-2.

用matlab软件分别绘制f(x)=x3和切线y=3x-2的图形，如图3(a). 可以看到，在点(1,1)附近曲线和切线非常靠近，但是离开x=1误差就比较大了.图3(b)和图3(c)在越来越小的区间上展示了函数f(x)和切线y的图形，图3(d)显示在包含1的很小的区间上，曲线和切线非常靠近，这时用计算机绘图已经不能区分这两条曲线了.这表明，在局部范围内，可微函数的性态就像一条直线.多元函数的微分思想和一元情形类似，我们举个更直观的例子来说明.大家都知道地球是圆的，但是为什么感觉我们所站的地方是平面，而不是想象中的曲面呢？这是因为地球表面可以看做是空间中的曲面，在其可微点的局部领域，地球的表面和它在这点处的切平面是近似重合的.

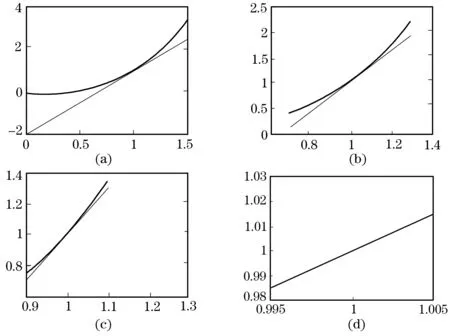
图3 函数f(x)=x3在可微点(1,1)处的性态

3 利用图形理解积分公式

在积分学中有很多公式结论，如果不加理解的直接死记硬背，恐怕是记不住的.教师可以通过图形等有效方法使学生记住这些有用的结论.下面举个例子来说明.

在一元积分学中大部分学生都可以很容易的利用Newton-Leibniz公式证明下面积分成立

但是，很少学生认真考虑这个结论的意义.为了增强学生对此结论的记忆，教师可以结合数学实验，让学生先画此积分的被积函数的几何图形，既可以加强matlab绘图软件的操作，又对此函数有所了解，进一步对积分结果有直观上的理解，可谓一举两得.然后再通过严格的证明论证这个结论.比如，不妨设f(x)=sin2xsin3x,g(x)=sin22x，通过matlab软件绘制曲线如图4(a)和图4(b).

(a) 函数f(x)的曲线 (b) 函数g(x)的曲线图4 函数f(x)和g(x)的曲线

利用函数图形的对称性，及定积分的几何意义，在函数非负时定积分值为与x轴围成的区域的面积，在函数小于零时，定积分值为与x轴围成的区域的面积的负值，所以

而最后一个积分很容易通过三角变换积分出来.我们相信，有了上面的两个图形，学生一定对定积分的几何意义有很深刻的了解，也很容易的记住一些积分结论.

4 分别利用通俗的语言和图形理解函数的凹凸性与极值

在讲到函数的凹凸性及函数的极值时，几乎所有教材都是先给出凸函数的定义，然后再用函数的一阶导函数的严格单调增或单调减来判断原函数是凸函数或凹函数，也可以用函数的二阶导函数是否大于零来判断，学生对此理解不深，记不住哪个是哪个，很容易搞混.

图5

我们可以用下面的很通俗的语言来描述凹凸函数，比如①学生每月的花费以越来越快的速度在上涨；②学生每月的花费继续增长，但是速度越来越慢.首先让学生琢磨这两句话，理解其表达的意思，然后绘制相应的函数图形，如图5(a)和图5(b).教师再分别解释，①其实是说明花费函数曲线的切线斜率在增加，花费函数是凸函数，而②的花费函数曲线的切线斜率在减少，花费函数是凹函数.函数的凹凸性就比较容易区分清楚了.

当然，也会有教师说，仍然有部分学生在判断函数极值和凹凸性时，左顾右盼的，拿不定主意.那么，我们也可以用下面简单有趣但是很形象的“脸谱图案”来表示，如图6.图6(a)是一个哭脸，两个减号表示眼睛闭着，代表函数的二阶导数为负，下弯的嘴形就代表局部极大值，相应函数就是凹函数，图6(b)是一个笑脸，两个加号当做眼睛，微笑的嘴形当然就代表局部极小值，当然原函数是凸函数了.我们相信，有这两个可爱的“脸谱图案”，学生一定能将函数的极值和凹凸性记清楚.

(a) 极大值和凹函数 (b) 极小值和凸函数图6 脸谱图案表示函数凹凸性和极值

5 结束语

本文探讨了如何借助几何图形理解高等数学中一些抽象的结论.通过案例说明，借助几何图形，可以直观、形象的理解高等数学中的一些概念和结论，把“令人生畏”的高等数学的教学变得“生动有趣”.特别是在探索教学改革的今天， 在教学中尽量把一些比较抽象、较难记住、难理解的知识结论，通过学生自己绘图，自己观察结论，以学生最容易接受的形式表达出来，对于减少学生的理解障碍，提高学习数学的兴趣有着重要积极的意义.

[参 考 文 献]

[1] 国家中长期教育改革和发展规划纲要(2010-2020年)[DB]. http:∥www.gov.cn/jrzg/2010-07/29/content_1667143.htm.

[2] 王绵森，马知恩. 工科数学分析基础(上册)[M]. 北京：高等教育出版社，2006:51-52.

[3] 李继成. 数学实验[M]. 北京：高等教育出版社，2006: 13-21.

[4] Dale Varberg, Edwin J Purcell, Steven E Rigdon. 微积分[M]. 北京：机械工业出版社，2009: 148-149.

[5] Colin Adams, Joel Hass, Abigail Thompson, 微积分之屠龙宝刀[M]. 长沙：湖南科学技术出版社，2004: 102-103.