ζ(2k)的一种简便算法
2014-09-17 06:52:00周华生
大学数学 2014年4期
周华生
(江苏常熟市中学 ,江苏常熟215500)
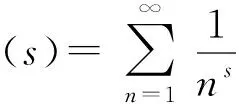
定理1设z∈,则

(1)
其中bn满足
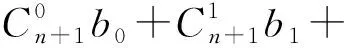
或
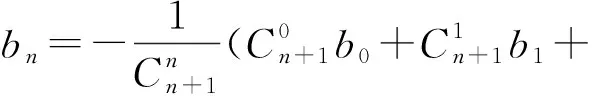
且b0=1,b2k+1=0(k∈+).

设t=2iz,则


比较tn的系数得b0=1,且有
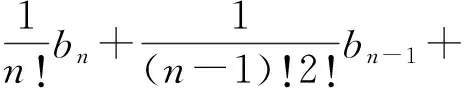
两边乘以(n+1)!,得
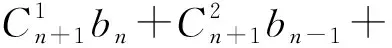
或

(2)
若将bn看成bn,上式可利用如下的二项式定理帮助记忆,即
(b+1)n+1-bn+1=0 (n=1,2,3,…).
由于zcotz为偶函数,故z2k+1的系数b2k+1=0(k∈+).
依次将n=1,2,3,…代入(2),由b0=1可逐步求得
将t换回到z,可得
(3)
zcotz还有另一种展开形式,我们有
定理2当|z|<π时,
证首先,考虑coszx是偶函数,故可以在(-π,π)上展开为余弦级数.又
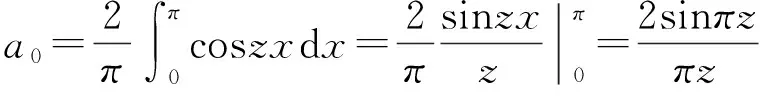
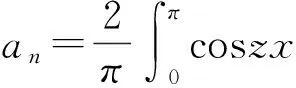

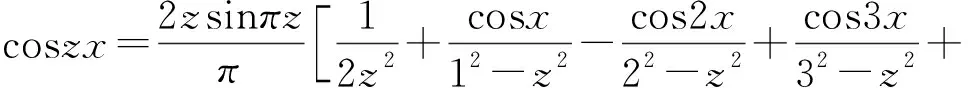
以x=π代入,得
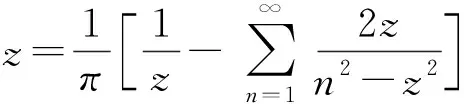
(4)
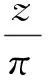
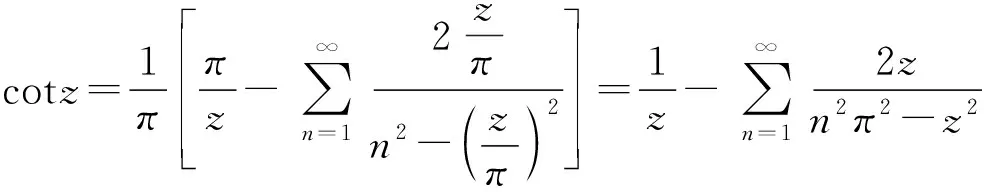
所以

又当|z|<π时,
故
(5)
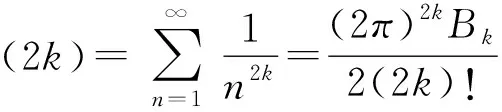
其中Bk=(-1)k-1b2k(k=1,2,3,…)称为贝努利数.
证比较(3),(5),zcotz两种展开式相等,令Bk=(-1)k-1b2k,可得
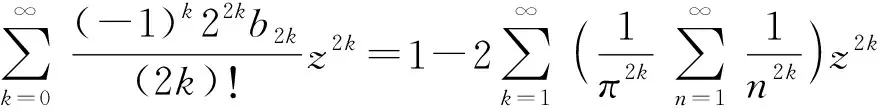
因为z2k的系数相等,故有
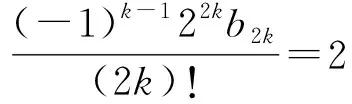
化简,可得ζ(2k)的表达式.
(6)
公式(6)称为欧拉公式,其中Bk称为贝努利数,且
由公式(6)可得
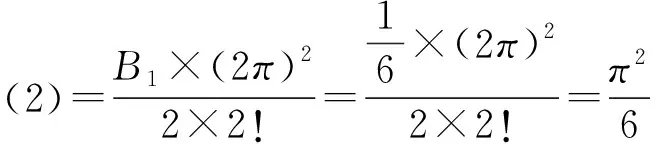
(华南工学院1979年研究生入学试题)
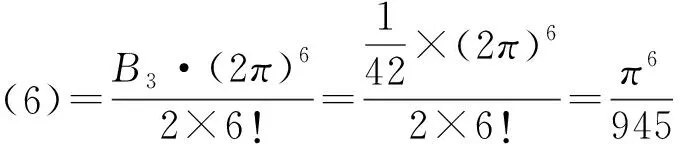
此外还可求得
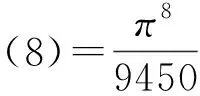
欧拉公式还有如下的一些应用:

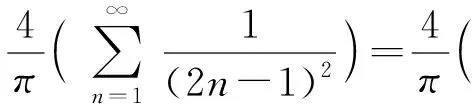
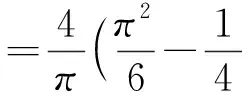
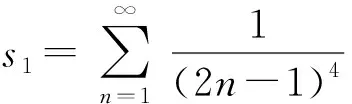


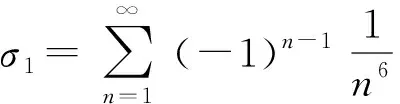
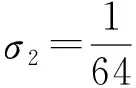
[参 考 文 献]
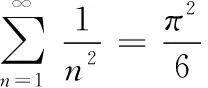
[3] 华罗庚.高等数学引论(第一卷第二分册)[M].北京:科学出版社,1979:282-284.
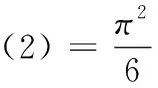
猜你喜欢
汽车观察(2022年12期)2023-01-17 02:20:42
小学生学习指导(高年级)(2022年10期)2022-11-04 06:20:50
哈哈画报(2022年1期)2022-04-19 11:27:20
车迷(2022年1期)2022-03-29 00:50:26
中学生数理化·七年级数学人教版(2017年3期)2018-01-20 12:45:54
数学小灵通·3-4年级(2017年9期)2017-10-13 08:11:04
中学生数理化·七年级数学人教版(2017年12期)2017-02-15 09:56:01
中学生数理化·七年级数学人教版(2017年12期)2017-02-15 09:56:01
中学生数理化·高一版(2016年9期)2016-05-14 09:03:49
中学数学杂志(高中版)(2016年1期)2016-02-23 01:14:41

