用傅里叶级数求自然数幂和

李卫高， 李兆强

(漯河医学高等专科学校, 漯河462002)

(1)

其中

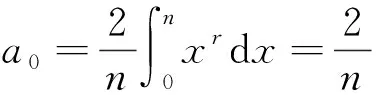
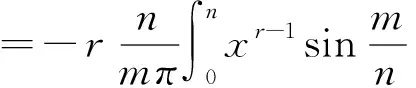
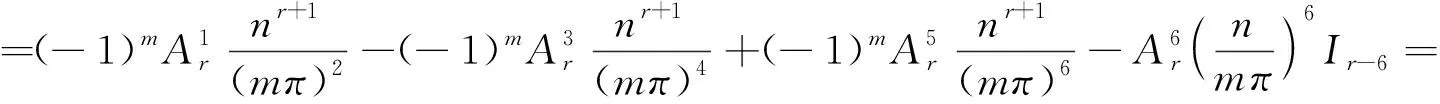
而

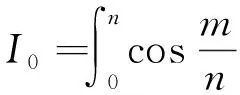
于是

为表示自然数幂和，在(1)式中依次令x=1,2,3,…,n，得到

……

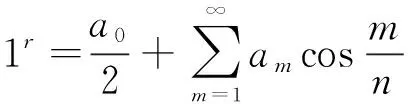
把以上n个等式相加，得

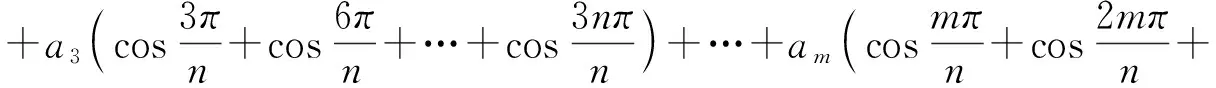
此时

m=2kn,k=1,2,3,….

易知这些项中每一个括号的和都等于n，于是

或者

(2)

例2r=3，m为偶数时，

代入(2)式，

r为偶数时，

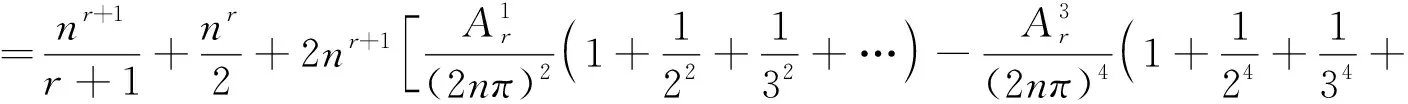
r为奇数时，

同理可得

为简便起见，把它们统一写成

(3)

不难看出，这种一般表达式和历史上伯努利幂和公式虽形式不同，但是相通的.同时和zeta函数建立了联系，(3)式本身包含了求ζ(2k)的计算方法，例如求ζ(2)，ζ(4).

令n=1,r=2，

令n=1,r=4，

[参 考 文 献]

[1] 陈传璋,等.数学分析(下册)[M].北京：高等教育出版社，1983.

[2] 罗见今．自然数幂和公式的发展[J]．高等数学研究，2004，7(4)：56-61.