(n-1)维曲面所围空间体积的计算公式
陈凌蛟
(东南大学吴健雄学院,南京210096)
1 引 言
在高等数学理论[1-6]中,对于求解光滑闭曲线(曲面)所围区域面积(体积)的问题,由于在方法上采用了Green公式,难以推广到n维空间求取光滑闭曲面所围区域的体积.本文则从变量代换的角度,用类似极坐标变换的方式,将闭区域的内部用它的边界表示出来,再利用重积分的变量代换公式,求出闭区域的面积.进一步地,将这一思路应用到高维空间当中,得出了高维空间中光滑闭曲面所围区域体积计算的一个新公式.文章的最后,给出了本文的新方法与新公式的几个应用举例,尤其在单纯形体积计算上,体现出了本文所得结果的实用价值.
2 简单闭区域面积计算公式新的证明
如引言所述,在一些高等数学的文献[5,6]里,求简单闭曲线所围区域面积的公式,是作为Green公式的一个推论给出的.Green公式在二维平面中确实有很广的应用[7],但由于Green公式本身是针对平面围线积分的,所以这种方法并不便于向n维空间做推广.本文为了利于把求闭曲线所围区域面积的公式推广向n维空间,给出了下面完全不同的证明方法.
定理1设D为平面上包含原点的有界区域,其边界为光滑的简单闭曲线

且满足
x′(t)y(t)-y′(t)x(t)≠0,
则D的面积为

证注意区域D可以表示为D=(x,y)|x=x(t)·u,y=y(t)·u,a≤t≤b,0≤u≤1,并记D*=(t,u)|a≤t≤b,0≤u≤1.
当u≠0时,

根据有界闭区域上重积分的变量代换定理,得到
关于定理1的几点注记:
注1 定理1中的条件x′(t)y(t)-y′(t)x(t)≠0是为了保证从xOy平面到tOu平面的映射满足一一对应关系.事实上,只要闭区域D内满足x′(t)y(t)-y′(t)x(t)≥0≤0,且等于0的所有点构成的点集Ds的测度为0,上述定理依然成立.特别地,当Ds为有限集时,定理成立.
注2 定理1中的条件“包含原点”是为了保证从xOy平面映射到tOu平面时,可以直接把区域D表示为D=(x,y)|x=x(t)·u,y=y(t)·u,a≤t≤b,0≤u≤1.而对于不包含原点的情形,根据积分与坐标平移的无关性,可以先将闭区域D做适当平移,使得D包含原点,这就又回到了定理1中的条件.
3 高维空间区域体积计算的新方法
如上节所述,本文对定理1给出新的证明方法是为了能够在n维空间做有效的推广.事实上,这一方法除了通过变量代换用高维区域的边界条件表示其内部外,只需要再结合n重积分换元公式[8],就可以推广到n维空间中.下面的定理对这一推广给出了完整的表述和证明.
定理2设Dn为n维空间上包含原点的有界区域,其边界为光滑的n-1维简单闭曲面
(x1u1,u2,…,un-1,x2u1,u2,…,un-1,…,xnu1,u2,…,un-1)|ai≤ui≤bi,1≤i≤n,
且满足
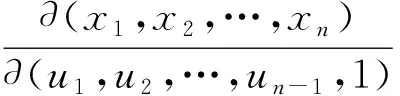
则它的体积为

证区域Dn可以表示为
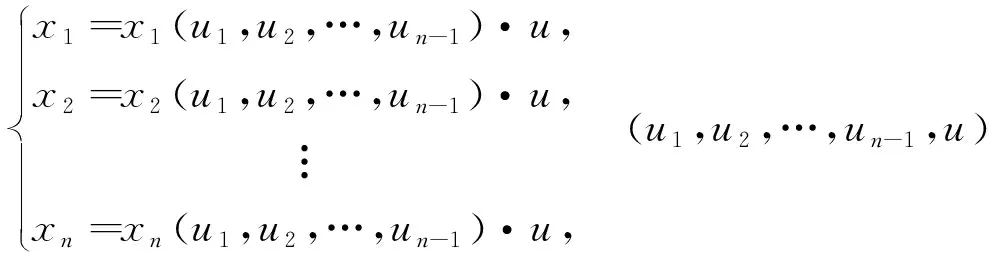
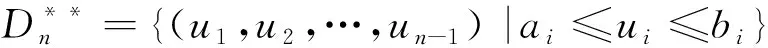

根据有界闭区域上重积分的变量代换定理,得到
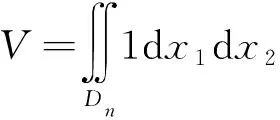
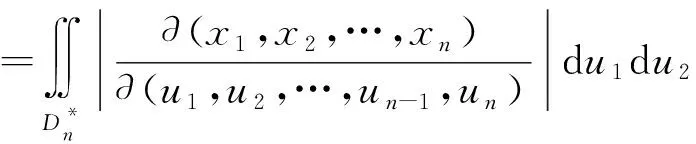



关于定理2的几点注记:
注3 类似于注记1的讨论,还可以在高维空间中论证,只要闭区域Dn内满足

且其等于零的所有点构成的点集Dns的测度为0, 上述定理依然成立.特别地,当Dns为有限集时,定理成立.
注4 在定理2中,n=2时,就得到定理1的结果;n=3时,就得到3维空间中闭区域的体积计算公式.
4 简单应用举例
接下来给出几个具体的算例.
1)设简单闭曲线
l=x(t),y(t)|x(t)=cost+a,y(t)=sint+b,t∈0,2π,
求l所围区域D的面积S.
解随着参数a,b的变化,闭区域D内并不总是包含原点.通过平移变换
将闭区域D映射到Ω=x*(t),y*(t)|x*(t)=cost,y*(t)=sint,t∈0,2π,则区域Ω是包含原点的.
注意到x*′(t)y*(t)-y*'(t)x*(t)=-sin2t-cos2t=-1<0,且平移变换前后对应区域的面积不变,可以应用定理1,有
由参数方程可以看出,区域D就是一个单位圆.上式所得结果与我们熟知的“单位圆面积为π”相吻合.
解椭球面的参数方程为:


3) 求标准n-单纯形Δn=(x1,x2,…,xn)∈,∀i,xi≥所围区域D的体积Vn.

当n≥3时,通过变量代换

则

故有

且等于零的所有点构成的点集测度为0,根据注记3,可以应用定理2,得到



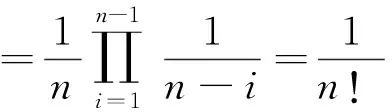
综上,即有

注5 本文所举的应用中,前面两个是较为平凡的情形,而第三个例子则较好地显示了本文所给新方法的精彩之处.n-单纯形在最优化算法、计算几何等领域中有广泛的应用[9],而求取标准n-单纯形的体积虽然只是一个基本的问题,却不是一件容易的事.单纯形理论中的求解方法[10]需要借用几何的观点,引进面的概念.分析数学里的处理方法[5]则需要采用数学归纳法.然而,本文所给出的新算法,可以通过巧妙地引入变量代换,直接计算出标准n-单纯形,既摆脱了对几何的依赖,又避免了数学归纳法的繁琐.由此可见,本文提供的新方法在求取高维区域体积问题上,具有一定的优势.
5 结束语
本文着重讨论了在已知边界情形下如何求解闭区域的面积(体积)的一种新方法,并将之推广到了n维空间,得到了一个全新的公式.这一方法可以看作是对Green公式求面积和Gauss公式求体积领域的统一和推广.给出的几个应用实例,体现了本文结果的意义,以及在高维区域体积计算领域里的实用价值.
致谢本文在撰写过程中,得到了东南大学数学系孙志忠教授和电气工程学院陈歆技教授的悉心指导和热心帮助,在此表示最衷心的感谢!
[参 考 文 献]
[1] Richard Courant, Fritz John. Introduction to calculus and analysis[M]. New York: Interscience Publishers,1965.
[2] Walter Rudin. Principles of Mathematical Analysis[M]. New York: Macgraw-Hill,1976.
[3] 菲赫金哥尔茨. 《微积分学教程》 [M].北京:高等教育出版社, 2006.
[4] 徐森林,薛春华. 《数学分析》[M].北京:清华大学出版社, 2006.
[5] 陈纪修,等. 《数学分析》 [M].北京:高等教育出版社, 2004.
[6] 同济大学数学系. 《高等数学》[M].北京:高等教育出版社, 2007.
[7] 蒲和平,李厚彪 何林芸. 从等周不等式谈Green公式的一个应用[J].大学数学,2013,29(2) :82-85.
[8] 袁俊华.n重积分换元公式的证明[J].大学数学,2013,29(2) :126-130.
[9] 燕子宗,等. 线性规划的单纯形法及其发展[J].计算数学,2007,29(1):1-14.
[10] 沈文选. 单形论导引[M].长沙: 湖南师范大学出版社, 2000.

