一类重积分解法的探讨

龚伟枫， 吴 洁

(1.华中科技大学光学与电子信息学院，湖北武汉430074； 2.华中科技大学数学与统计学院，湖北武汉430074)

在2010年全国硕士生入学统一考试数学三中有如下试题：

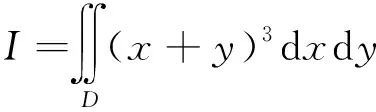
图1

解法1区域D如图1所示.

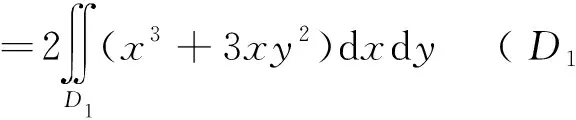
=14/15 .

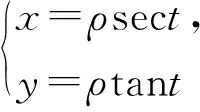
说明：

(i)ρ和t并没有几何意义，它们仅表示关于x,y的某个表达式的值.

图2 图3

图4 图5

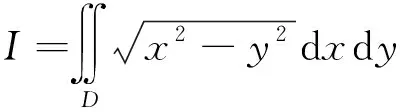
解法1利用直角坐标并由对称性，得

可见，当被积函数含x2-y2，用“双曲坐标变换”避免了复杂的计算过程.例3将说明当被积函数和积分区域同时含有x2-y2项时，采用“双曲坐标变换”的优越性.

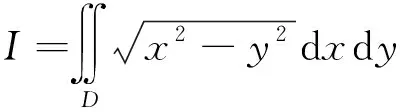
解法2利用直角坐标并由对称性，得

由于后面的积分过程比较复杂，积分结果由以下Matlab程序提供.

syms y;

f=inline(′sqrt(1+y.^2)′);

i=quad(f,0,1);

f1=inline(′y.^2.*log(sqrt(1+y.^2)+1)′);

i1=quad(f1,0,1);

i2=quad(′sqrt(2).*y.^2′,0,1);

f3=inline(′y.^2.*log((sqrt(2)+1).*y)′);

i3=quad(f3,0,1);

i0=i-i1-i2+i3;

运行结果：

i0=0.5876.

两种方法的计算结果一致，说明了运用“双曲坐标变换”方法的正确性.

类似于极坐标，利用双曲坐标变换还可以处理一些直角坐标无法计算的问题.

注 该题被积函数为ey2·e-x2，在直角坐标系下，无论是先对x还是先对y积分，均无法积出.

“双曲坐标变换”的方法也可以运用到三重积分的计算上.如果单叶双曲面、双叶双曲面、圆锥面、双曲抛物面或双曲柱面的标准形式出现在积分区域边界上或被积函数中，可以根据需要做相应的变换，变换的形式可以多样.

图6

因此

解法2利用对称性，

例5的积分区域含单叶双曲面，且单叶双曲面在积分区域边界上.对比两种解法可以看出 “双曲坐标变换”更加直观和自然.例6则根据区域的不同边界选取了不同的“双曲坐标变换”，均可达了到简化计算的效果.

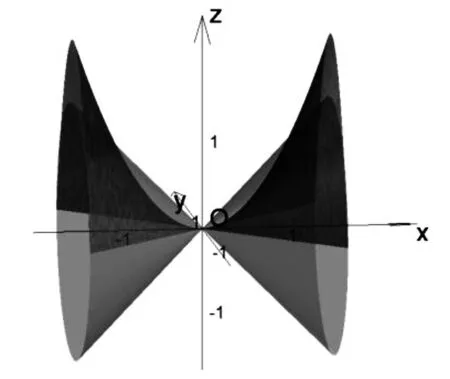
图7

解法1利用对称性，

因此

本文引入的“双曲坐标变换”实际上是重积分极坐标代换的一种推广.极坐标代换便于解决积分区域为圆域、被积表达式中含有平方和项的重积分问题，从前面几例可以看出，“双曲坐标变换”适用于积分区域边界含有双曲线、被积表达式中含有平方差项的重积分问题.在这类问题上，这种变换有着不可替代的优越性.应当指出的是，使用“双曲坐标变换”时积分区域受到一定限制，积分区域不应当越出该变换可以使用的范围，否则该方法失效.

[参 考 文 献]

[1] 华中科技大学数学系. 微积分学[M].3版.北京：高等教育出版社, 2008.