Chetaev型非完整系统Nielsen方程Lie对称性导致的一种守恒量*

徐瑞莉 方建会 张斌 王菲菲

(中国石油大学理学院，青岛 266580)

Chetaev型非完整系统Nielsen方程Lie对称性导致的一种守恒量*

徐瑞莉†方建会 张斌 王菲菲

(中国石油大学理学院，青岛 266580)

研究Chetaev型非完整系统Nielsen方程Lie对称性导致的一种守恒量，给出无限小群变换下Chetaev型非完整系统Nielsen方程Lie对称性的确定方程，得到Chetaev型非完整系统Nielsen方程Lie对称性直接导致的一种守恒量及其存在条件，并举例说明结果应用．

非完整系统， Nielsen方程， Lie对称性， 守恒量

引言

对称性原理是物理学中更高层次的法则［1］．寻求守恒量是对称性理论的重要用途之一，动力学系统的对称性与守恒量研究在数学、力学和物理学中具有极其重要的理论意义和实际意义．近代分析力学中寻求约束力学系统守恒量的方法主要有Noether对称性［2］、Lie 对称性［3］和 Mei对称性［4］，这三种对称性导致的守恒量主要有Noether守恒量、Hojman守恒量和 Mei守恒量［5］．近年来，人们对各类力学系统Noether对称性、Lie对称性和Mei对称性导致的Noether守恒量、Hojman守恒量和Mei守恒量的研究取得了一系列重要成果［6－14］．随着其研究的不断发展，寻找新守恒量的研究受到了人们的关注．文献［15］给出了Lagrange系统Lie对称性直接导致的一种新守恒量，文献［16］进一步研究了Lagrange系统Noether对称性和Mei对称性导出这种新守恒量，Nucci［17］在文献［16］的基础上对其中算例具有的这种新守恒量做了更细致的研究．

约束动力学系统的各种运动方程可分为三大重要体系:Lagrange体系、Nielsen体系和Appell体系．关于Nielsen体系中Nielsen方程的对称性与守恒量已有许多研究．王树勇和梅凤翔［18］给出了Nielsen方程Noether对称性与Mei对称性的关系，方建会［19］等研究了非保守力学系统Nielsen方程的Mei对称性，乔永芬［20］等研究了非完整系统相对论变质量Nielsen方程的Mei对称性和守恒量，许学军［21］等给出了非保守 Nielsen方程的Mei对称性导致的非Noether守恒量，文献［22］研究了相对运动动力学系统Nielsen方程Lie对称性与Hojman守恒量．然而，Nielsen方程对称性导致文献［15］给出的新守恒量的研究成果还未见报道．本文在文献［15］的基础上研究Chetaev型非完整系统Nielsen方程Lie对称性导致的这种新守恒量，给出无限小群变换下Chetaev型非完整系统Nielsen方程Lie对称性的确定方程，得到Chetaev型非完整系统Nielsen方程Lie对称性直接导致的这种新守恒量的形式及其存在条件．

1 Nielsen方程的Lie对称性

设力学系统的位形由n个广义坐标qs(s=1，…，n)确定，L=L(t，q，q)为系统的Lagrange函数，Qs=Qs(t，q，q)为非势广义力，其运动受到g个双面理想Chetaev型非完整约束

约束(1)加在虚位移δqs上的Chetaev条件为

由D＇Alembert－Lagrange原理和虚位移上的Chetaev条件(2)，用Lagrange乘子法可得系统的Nielsen方程为

其中λβ为约束乘子，方程(3)可写为

其中Ns为Nielsen算子

Λs为广义非完整约束反力

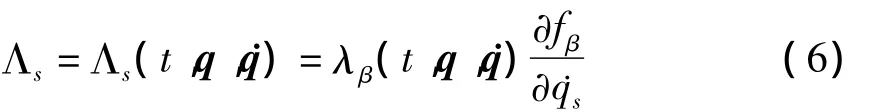
假设系统(3)非奇异，即

可求出所有广义加速度，记作

引入时间和广义坐标的无限小变换

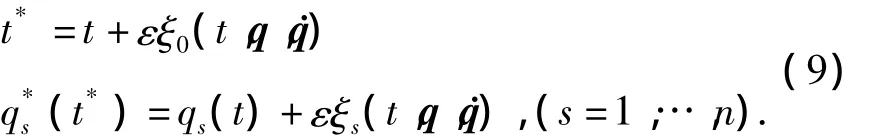
其中ε为无限小参数，ξ0，ξs为无限小变换生成元．

根据力学系统的Lie对称性理论［1］，非完整系统Nielsen方程Lie对称性的确定方程为

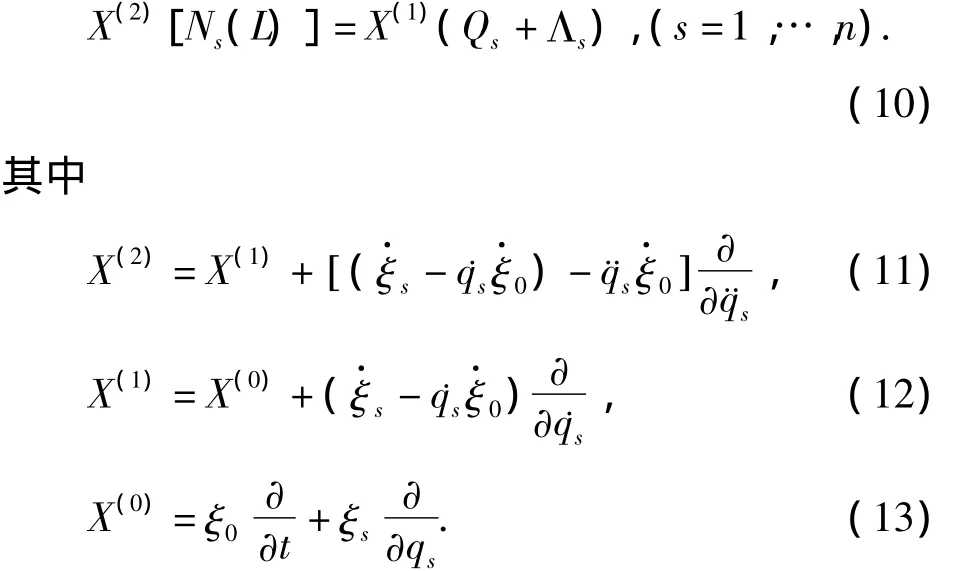
方程(8)对应的Lie对称性的确定方程表示为

可以证明Lie对称性的确定方程的两种表示(10)和(14)是等价的．

于是，可得到如下判据:

判据1 如果存在无限小生成元ξ0，ξs满足确定方程(10)或(14)，那么相应不变性为与非完整系统(1)，(3)相应的完整系统(4)或(8)的Lie对称性．

非完整约束力学方程(1)在无限小变换(9)下的不变性归为如下限制方程

判据2 如果存在无限小生成元ξ0，ξs满足确定方程(10)或(14)以及限制方程(15)，那么相应不变性为非完整系统(1)，(3)的弱Lie对称性．

考虑到等时变分与非等时变分有如下关系

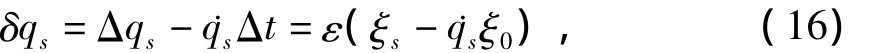
将(16)式代入(2)式，有

称方程(17)为附加限制方程．

判据3 如果存在无限小生成元ξ0，ξs满足确定方程(10)或(14)，限制方程(15)以及附加限制方程(17)，那么相应不变性为非完整系统(1)，(3)的强Lie对称性．

2 Nielsen方程的Lie对称性的结构方程和守恒量

已有的研究表明［5］，非完整系统的Lie对称性可以直接导致Hojman守恒量．下面研究非完整系统Lie对称性直接导致的一种新守恒量及其存在条件．命题1 如果非完整系统(1)，(3)的Lie对称性的生成元ξ0，ξs以及规范函数G=G(t，q，q)满足如下结构方程

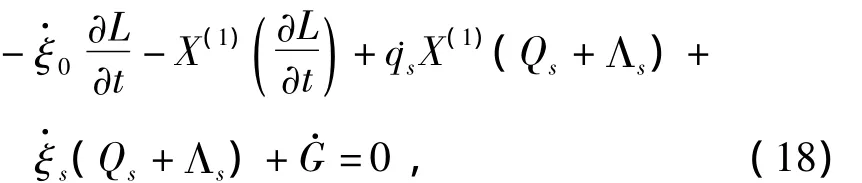
则相应完整系统的Lie对称性直接导致一种守恒量

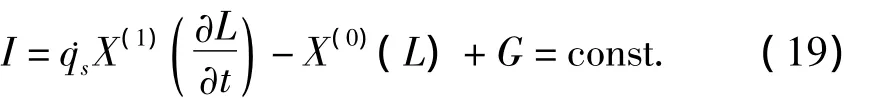
证明 求守恒量I对时间t的导数，得

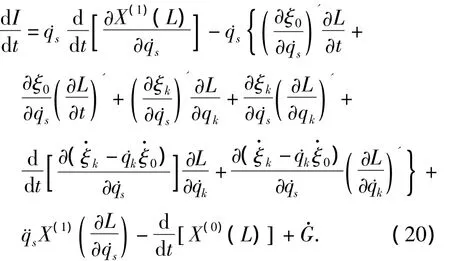
由(12)式易得

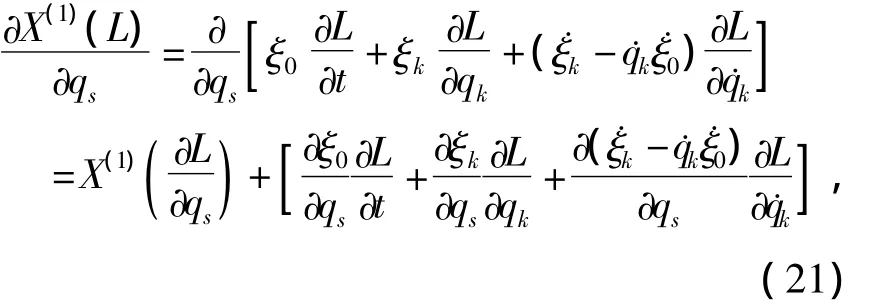
结合(20)和(21)式，有

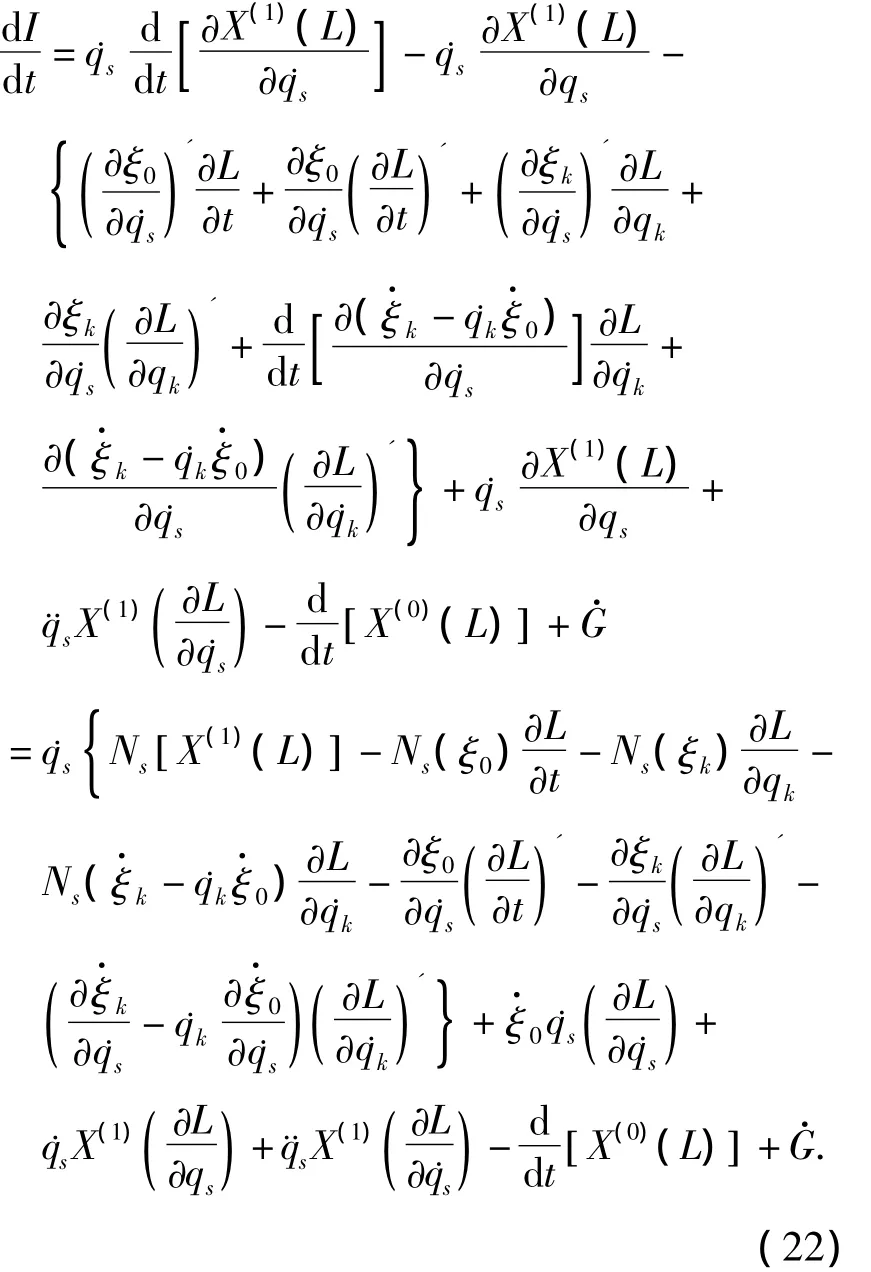
考虑如下关系式

由(23)和(24)式得

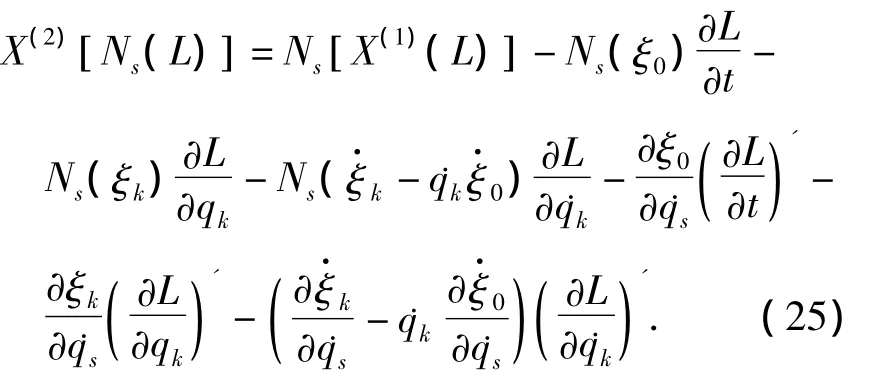
将(25)式代入(22)式，得

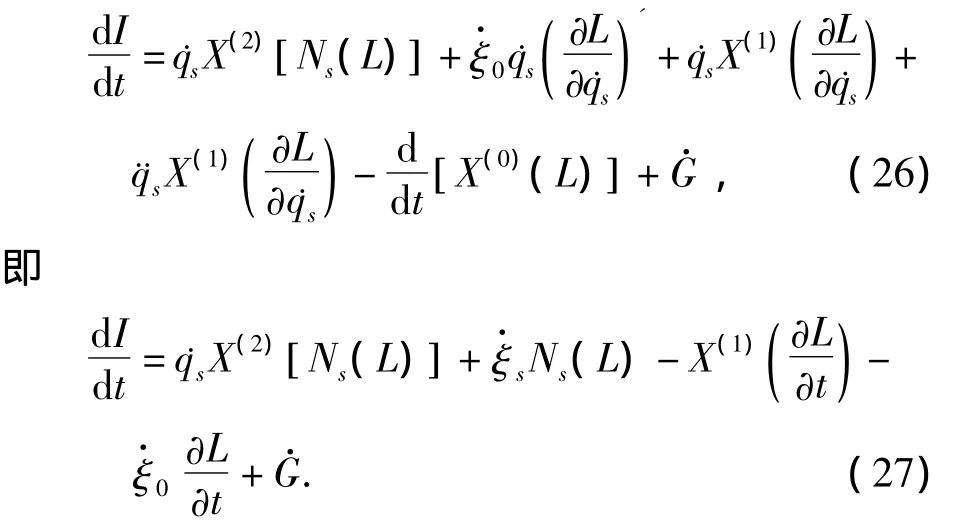
由(27)式，结合(4)，(10)和(18)式可得

命题1得证．

利用命题1，判据2和判据3容易得到如下命题:命题2 对于Chetaev型非完整系统(1)，(3)，如果存在无限小生成元ξ0，ξs满足确定方程(10)或(14)以及限制方程(15)，且存在规范函数G=G(t，q，q)使得方程(18)成立，则非完整系统的弱Lie对称性直接导致守恒量(19)．

命题3 对于Chetaev型非完整系统(1)，(3)，如果存在无限小生成元ξ0，ξs满足确定方程(10)或(14)，限制方程(15)以及附加限制方程(17)，且存在规范函数G=G(t，q，q)使得方程(18)成立，则非完整系统的强Lie对称性直接导致守恒量(19)．

对于一般完整系统，Λs=0，由上述命题可得推论:推论1 对一般完整系统，如果存在无限小生成元ξ0，ξs满足确定方程

X(2)Ns(L[ ])=X(1)(Qs)，(s=1，…，n)，(29)

且存在规范函数G=G(t，q，q)满足结构方程

则一般完整系统的Lie对称性可直接导致守恒量(19)．

对于完整保守系统，Qs=0，Λs=0，由以上命题可得推论:

推论2 对完整保守系统，如果存在无限小生成元ξ0，ξs满足确定方程

且存在规范函数G=G(t，q，q)满足结构方程

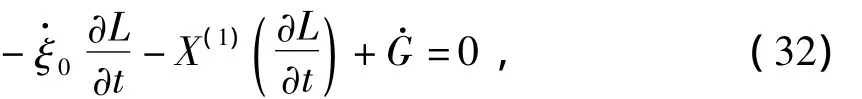
则完整保守系统的Lie对称性可直接导致守恒量(19)．

3 算例

非完整系统的Lagrange函数为

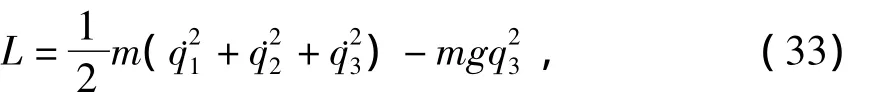
系统非完整约束力学方程为

非势广义力Qs=0，试研究非完整系统Nielsen方程Lie对称性导致的一种守恒量．

将(33)，(34)式代入方程(3)，得

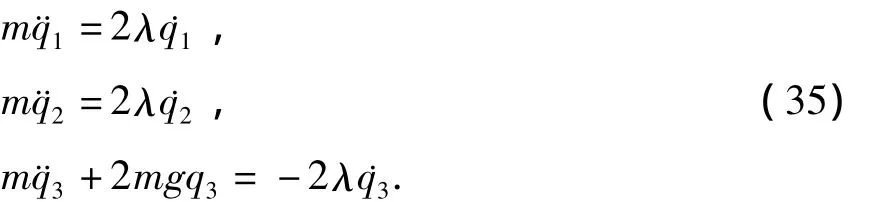
对(34)式求时间t的导数

结合(35)式和(36)式，可得

将(37)式代入方程(35)，得

由确定方程(14)和(38)式得

根据限制方程(15)得

根据附加限制方程(17)得

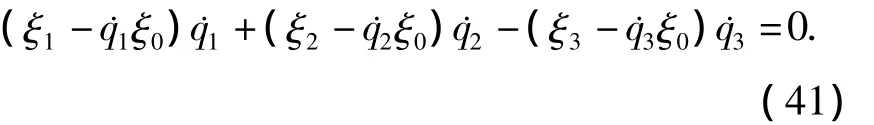
联立方程(39)、(40)和(41)，求解方程组可以得到如下无限小生成元

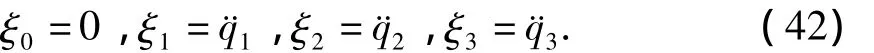
将生成元(42)代入结构方程(18)，存在

利用生成元(42)，规范函数(43)和命题3可得

4 结论

本文给出了无限小群变换下Chetaev型非完整系统Nielsen方程Lie对称性的确定方程，得到了Chetaev型非完整系统Nielsen方程Lie对称性直接导致的一种守恒量及其存在条件．该守恒量是与Chetaev型非完整系统Nielsen方程Lie对称性直接导致的Hojman守恒量，间接导致的Noether守恒量和Mei守恒量不同的另一种守恒量．本文结果更具一般意义，对非完整系统、一般完整系统和完整保守系统都适用．若将Nielsen算子转换为与之等价的Euler算子，在Qs=0，Λs=0的条件下，本文结果将回到文献［15］的结果．

1 梅凤翔．李群李代数对约束力学系统的应用．北京:科学出版社，1999(Mei F X．Application of Lie groups and Lie algebras to constrained mechanical systems．Beijing:Science Press，1999(in Chinese))

2 Noether A E．Invariante variations problem．Nachr．Akad．Wiss．Gottingen Math．Phys，1918，KI II:235 ～237

3 Lutzky M．Dynamical symmetries and conserved quantities．Journal of Physics A:Mathematical and General，1979，12(7):973～981

4 Mei F X．From invariance of Lagrange system．Journal of Beijing Institute of Technology，2000，9(2):120～124

5 梅凤翔．约束力学系统的对称性与守恒量．北京:北京理工大学出版社，2004(Mei F X．Symmetries and conserved quantities of constrained mechanical systems．Beijing:Beijing Institute of Technology Press，2004(in Chinese))

6 罗绍凯．Hamilton系统的Mei对称性、Noether对称性和Lie对称性．物理学报，2003，52(12):2941～2944(Luo S K．Mei symmetry，Noether symmetry and Lie symmetry of Hamilton system．Acta Physica Sinica，2003，52(12):2941～2944(in Chinese))

7 郭永新，尚玫，罗绍凯．Birkhoff系统的Poincar_Cartan积分不变量．应用数学和力学，2003，24(1):62～66(Guo Y X，Shang M，Luo S K．Poincar_Cartan integral invariants of Birkhoffian systems．Applied Mathematics and Mechanics，2003，24(1):62～66(in Chinese))

8 梅凤翔．完整力学系统的三类对称性与三类守恒量．动力学与控制学报，2004，2(1):28～31(Mei F X．Three kinds of symmetries and three kinds of conserved quantities for holonomic systems．Journal of Dynamics and Control，2004，2(1):28～31(in Chinese))

9 张毅．广义经典力学系统的对称性与Mei守恒量．物理学报，2005，54(7):2980～2984(Zhang Y．Symmetries and Mei conserved quantities for systems of generalized classical mechanics．Acta Physica Sinica，2005，54(7):2980～2984(in Chinese))

10 Zhang H B，Chen L Q．The united form of Hojman＇s conservation law and Lutzky＇s conservation law．Journal of the Physical Society of Japan，2005，74(3):905～909

11 Wu H B．Lie－form invariance of the Lagrange system．Chinese Physics，2005，14(3):452～454

12 Jia L Q，Zhang Y Y，Luo S K．Hojman conserved quantity for nonholonomic systems of unilateral non－Chetaev type in the event space．Chinese Physics，2007，16(11):3168～3175

13 Chen X W，Liu C，Mei F X．Conformal invariance and Hojman conserved quantities of first order Lagrange systems．Chinese Physics B，2008，17(9):3180～3184

14 Fu J L，Chen B Y，Chen L Q．Noether symmetries of discrete nonholonomic dynamical systems．Physics Letters A，2009，373:409～412

15 Fang J H．A new type of conserved quantity of Lie symmetry for the Lagrange system．Chinese Physics B，2010，19(4):040301

16 Fang J H，Zhang M J，Zhang W W．A new type of conserved quantity induced by symmetries of Lagrange system．Physics Letters A，2010，374:1806～1811

17 Nucci M C．Many conserved quantities induced by Lie symmetries of a Lagrangian system．Physics Letters A，2011，375:1375～1377

18 Wang S Y，Mei F X．On the form invariance of Nielsen equations．Chinese Physics，2001，10(5):373 ～375

19 方建会，薛庆忠，赵嵩卿．非保守力学系统Nielsen方程的形式不变性．物理学报，2002，51(10):2183～2185(Fang J H，Xue Q Z，Zhao S Q．Form invariance of Nielsen equation of a nonconservative mechanical system．Acta Physica Sinica，2002，51(10):2183～2185(in Chinese))

20 Qiao Y F，Zhao S H，Li R J．Form invariance and conserved quantities of Nielsen equations of relativistic variable mass nonholonomic systems．Chinese Physics，2004，13(3):292～296

21 许学军，梅凤翔，秦茂昌．非保守Nielsen方程的形式不变性导致的非Noether守恒量．物理学报，2004，53(12):4021～4025(Xu X J，Mei F X，Qin M C．A non－Noether conserved quantity constructed using form invariance for Nielsen equation of a non－conservative mechanical system．Acta Physica Sinica，2004，53(12):4021～4025(in Chinese))

22 Wang X X，Sun X T，Zhang M L，Xie Y L，Jia L Q．Lie symmetry and Hojman conserved quantity of a Nielsen equation in a dynamical system of relative motion with Chetaev－type nonholonomic constraint．Chinese Physics B，2011，20(12):124501

*The Natural Science Foundation of Shandong Province of China(ZR2011AM012)，and the Postgraduate＇s Innovation research Foundation of China University of Petroleum(East China)(13CX06005A)

† Corresponding author E－mail:w13666363629@163．com

A TYPE OF CONSERVED QUANTITY OF LIE SYMMETRY FOR
NONHOLONOMIC SYSTEM OF NIELSEN EQUATION OF CHETAEV'S TYPE*

Xu Ruili†Fang Jianhui Zhang Bin Wang Feifei
(College of Science，China University of Petroleum，Qingdao266580，China)

This paper studied a type of conserved quantity deduced by the Lie symmetry for nonholonomic system with Chetaev－type of the Nielsen equation．Firstly，the determining equations of the Lie symmetry for nonholonomic system with Chetaev－type of the Nielsen equation were given under the infinitesimal transformation of groups．Secondly，the conditions of the existence of the type of conserved quantity of the system as well as its forms were obtained．And finally，an example was given to illustrate the application of the results．

nonholonomic system， Nielsen equation， Lie symmetry， conserved quantity

9 March 2013，

23 April 2013．

10．6052/1672－6553－2013－069

2013－03－09 收到第 1 稿，2013－04－23 收到修改稿．

*山东省自然科学基金(ZR2011AM012)、中国石油大学(华东)研究生自主创新科研计划项目(13CX06005A)

E－mail:w13666363629@163．com