异质性和时滞作用下神经元网络的共振动力学*
贾雁兵 杨晓丽† 孙中奎
(1.陕西师范大学,数学与信息科学学院,西安 710062)(2.西北工业大学,应用数学系,西安 710072)
异质性和时滞作用下神经元网络的共振动力学*
贾雁兵1杨晓丽1†孙中奎2
(1.陕西师范大学,数学与信息科学学院,西安 710062)(2.西北工业大学,应用数学系,西安 710072)
利用参数互异的Fitzhugh-Nagumo神经元构建了含耦合时滞的无标度神经元网络模型,通过数值模拟的方法,提出研究参数异质性和耦合时滞影响下神经元网络的共振动力学.结果发现,当耦合项中不含时滞时,适中的参数异质性能够使得神经元网络对外界弱周期信号的响应达到最优,即适中的参数异质性能够诱导神经元网络的共振响应,而且异质性诱导共振对耦合强度具有鲁棒性.更重要的是,耦合时滞对参数异质性作用下神经元网络的共振特性也有着显著性影响.当时滞约为信号周期的整数倍时,神经元网络能够周期性地出现共振现象,即适当的耦合时滞能够诱导神经元网络的多重共振,而且这种现象在异质性参数的适当范围内都能明显出现.
共振, 异质性, 时滞, 神经元网络, 谱放大因子
引言
2013-07-31 收到第 1 稿,2013-09-23 收到修改稿.
*国家自然科学基金(11272258,11172342)和中央高校基本科研业务费专项资金(GK201302001)资助项目
在过去的几十年里,许多研究者致力于研究噪声和非线性系统的相互作用.一些经典的现象如随机共振[1]、相干共振[2]、噪声诱导或增强同步[3-4]、噪声诱导相变[5]等见证了噪声对非线性系统有序动力学的积极影响.而且,研究对象也从简单的低维系统,逐渐扩展到耦合系统以至复杂网络系统,有兴趣的读者可参考综述文献[6-8].
对于网络系统,出于数学模型的简化,大部分研究工作认为所有的耦合单元是完全相同的.事实上,许多真实体系如生物网络和社会网络等,网络的个体之间往往是存在差异的.这种差异性在理论研究中通常通过模型方程中的某些关键参数不同来体现,它被称为参数异质性[9,10].类似于噪声,参数异质性对网络系统的混沌、同步、共振等集体动力学具有深刻的影响.例如文献[11]报道了最近邻耦合的单摆振列中,摆长多样性能够将单摆振子由混沌运动转变为周期运动;在神经元网络中,参数异质性可以将神经元由振动状态转变到可激状态[12],也能够增强网络的相干共振[9,13];在 Josephson结阵列中,Braiman等发现参数异质性对同步动力学具有增强作用[14].
特别地,Tessone等于2006年在PRL上报道了在全局耦合的神经元或双稳振子网络中,模型参数的差异性能够增强网络系统对弱周期信号的响应并引起共振现象[10].相对于经典的噪声诱导随机共振,这种现象被称为异质性诱导共振.随后,异质性诱导共振在转子体系[15]、电子电路[16]、细胞钙体系[17]等耦合体系中得到了广泛的研究.最近,异质性与网络结构、噪声、时滞等因素的相互影响也引起了一些学者的关注.例如,在神经元网络中,Gassel等研究了噪声与参数异质性诱导共振的关系,发现噪声的出现使得诱导共振出现的参数异质性减小[18];针对由双稳振子构成的小世界网络系统,吴丹等发现随机长程连接能够增强异质性诱导的共振,而时滞却对共振有削弱作用[19].
在神经科学中,耦合的神经元之间是存在差异的,这意味着神经元网络模型中参数异质性普遍存在[9,10].同时,由于动作电位沿轴突的有限传播速度以及突触间隙的存在,神经信息的传递存在时滞效应[20].因此,探索参数异质性与耦合时滞对神经元网络的集体动力学的影响有着重要的理论意义和潜在的应用价值.
已有的研究结果表明,参数异质性能够诱导全局耦合的神经元网络[10]和小世界神经元网络[21]的共振.然而,大脑皮层中一些区域内神经网络的连接形式具有无标度特性[22].那么,参数异质性能否诱导无标度神经元网络的共振?另外,在噪声的作用下,时滞能够诱导由全同神经元耦合构成的神经元网络的多重共振响应[23-25].那么,在参数异质性作用下,时滞对非全同神经元构成的神经元网络的共振动力学又有着怎样的影响呢?通过查阅文献,我们发现这些问题还没有得到研究.本文将通过构造节点上是Fitzhugh-Nagumo(FN)神经元的无标度神经元网络,并利用数值模拟方法来探讨参数异质性和耦合时滞对神经元网络共振动力学的关键影响.
1 神经元网络模型和研究方法
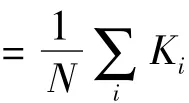
我们将FN神经元作为BA无标度网络的节点,在外界弱周期信号激励下,神经元网络的动力学方程为
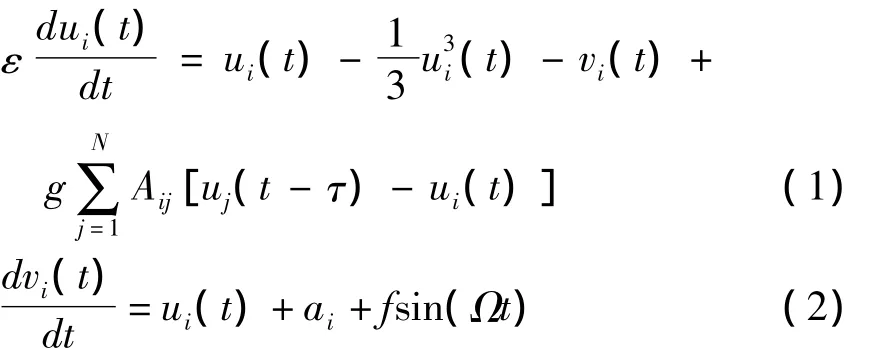
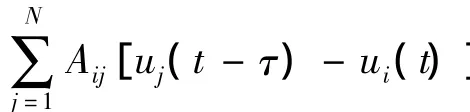
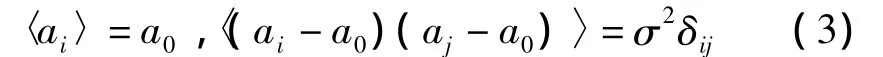
显然,σ决定不同神经元特征参数的差异性程度:当σ=0时有ai=a0成立,即N个神经元完全相同;当σ>0时,不同神经元的特征参数存在差异,而且σ越大,差异性就越显著.因此,我们也称σ为异质性参数.另外,fsin(Ωt)表示幅值为f、频率为Ω=2π/T的弱周期信号(T代表周期信号的周期).在以下研究中,我们固定ε=0.01,a0=1.12,f=0.05,T=5.0,并假定 ai是服从正态分布的随机变量.
为了定量刻画系统对激励信号的响应,我们引入谱放大因子η[10],其定义为


2 主要结果
在这一部分,我们首先讨论当方程(1)中的耦合项不含时滞(即τ=0时),神经元网络在参数异质性作用下的共振响应.然后,我们在耦合项中引入时滞,并探究时滞对神经元网络共振特性的影响.
2.1 参数异质性诱导神经元网络的共振响应
当耦合项中的时滞τ为0时,我们来研究异质性参数σ对神经元网络集体动力学的显著性影响.首先通过时空图来刻画神经元网络的时空动力学.当g=0.01时,图1刻画了不同σ取值下神经元网络的时空图.由图1可以观察到参数异质性对耦合神经元的放电行为产生了深刻的影响.当σ=0时,弱周期信号激励仍不足以使原本处于静息态的神经元产生放电行为,此时所有耦合神经元都没有放电,如图1(a)所示.随着σ的增大,部分神经元的特征参数减小而产生放电行为,放电神经元通过耦合作用带动其它神经元也放电,如图1(b)所示.有趣的是,当σ取值大小适中时,时空图达到了一个最规则状态,如图1(c)所示,此时不同神经元的放电动力学基本同步,而且绝大部分神经元放电周期约为5.0,这与弱周期信号的节律一致.但是,随着σ的进一步增大,大的异质性参数σ导致神经元的特征参数ai的分布比较广泛,这使得小部分神经元的特征参数远大于1.0而不能放电,同时也使得部分放电神经元的放电节律不能跟随弱周期信号的节律,如图1(d)与图1(e)所示,神经元网络的时空图反而又变的不规则了,耦合神经元的放电节律与弱周期信号节律的一致性被破坏.以上现象说明当异质性参数取值大小适中时,神经元网络的集体动力学对弱周期激励的响应达到了最优,即适中的参数异质性能够诱导神经元网络的共振行为.
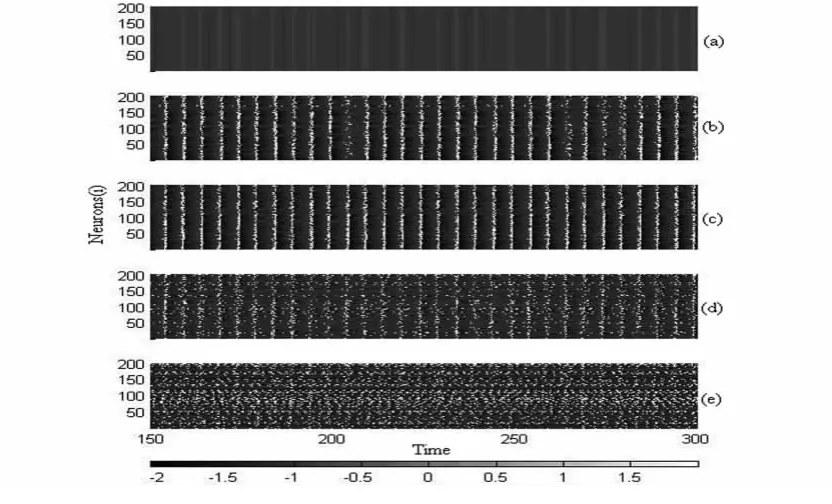
图1 g=0.01时,不同σ取值下神经元网络的时空图:(a)σ =0;(b)σ =0.055;(c)σ =0.07;(d)σ =0.12;(e)σ =0.3Fig.1 The space-time plots of coupled neurons on the networks for different σ:(a)σ =0;(b)σ =0.055;(c)σ =0.07;(d)σ =0.12 and(e)σ =0.3 when g=0.01
进一步地,下面借助于谱放大因子η(方程(4))来定量刻画神经元网络对弱周期信号的响应.当耦合强度为g=0.01时,图2刻画了谱放大因子η随着异质性参数σ变化的曲线(带实心方格的曲线).如图所示,随着σ的增大,η先增大后减小,并当σ≈0.07时达到最大值.该现象意味着适中的参数异质性能够诱导无标度神经元网络的共振响应,这与图1中定性分析的结果相一致.
另外,图2也给出了耦合强度取其它值(如g=0.005,0.02,0.05,0.08 时),η随着σ的演化曲线.不难发现,对固定的g,随着σ的增大,η总是先增大再减小,并在适中的σ处达到最大值.这表明神经元网络中异质性诱导共振对耦合强度具有鲁棒性.同时,我们也发现随着耦合强度的增加,曲线的峰值先增大再减小,这说明存在一个适中的耦合强度,使得神经元网络的共振特性最佳.
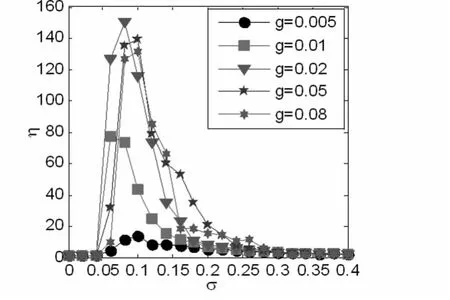
2 对不同的耦合强度,谱放大因子η随着异质性参数σ变化的曲线Fig.2 The dependence of η on σ for different coupling strength
2.2 时滞诱导神经元网络的多重共振响应
在上一节的研究基础上,下面在耦合项中引入耦合时滞,进一步研究时滞对异质性诱导的共振动力学的影响.不失一般性,固定异质性参数σ=0.07,耦合强度g=0.01.首先通过时空图来刻画时滞对神经元网络时空动力学的影响.图3给出不同时滞作用下神经元网络的时空图.
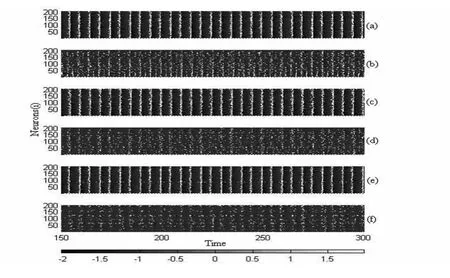
图3 异质性参数σ=0.07、耦合强度g=0.01时不同τ取值下神经元网络的时空图:(a)τ=0;(b)τ=2.5;(c)τ=5.0;(d)τ=7.5;(e)τ =10.0;(f)τ=11.0Fig.3 The space- time plots of coupled neurons on the networks for different τ:(a)τ=0;(b)τ=2.5;(c)τ=5.0;(d)τ=7.5;(e)τ=10.0 and(f)τ=11.0 when σ =0.07 and g=0.01
由图3可知,随着时滞的增加,时空图间歇性地呈现规则和不规则状态:当τ=0、5.0和10.0时,分别如图3(a)、3(c)和3(e)所示,时空图呈现规则状态,此时耦合神经元的放电行为基本达到同步,而且绝大部分神经元的放电周期约为5.0,这与弱周期信号的节律一致;而当τ=2.5、7.5和11.0时,分别如图3(b)、3(d)和3(f)所示,时空图呈现不规则状态,而且神经元的放电节律与弱周期信号的节律不一致.
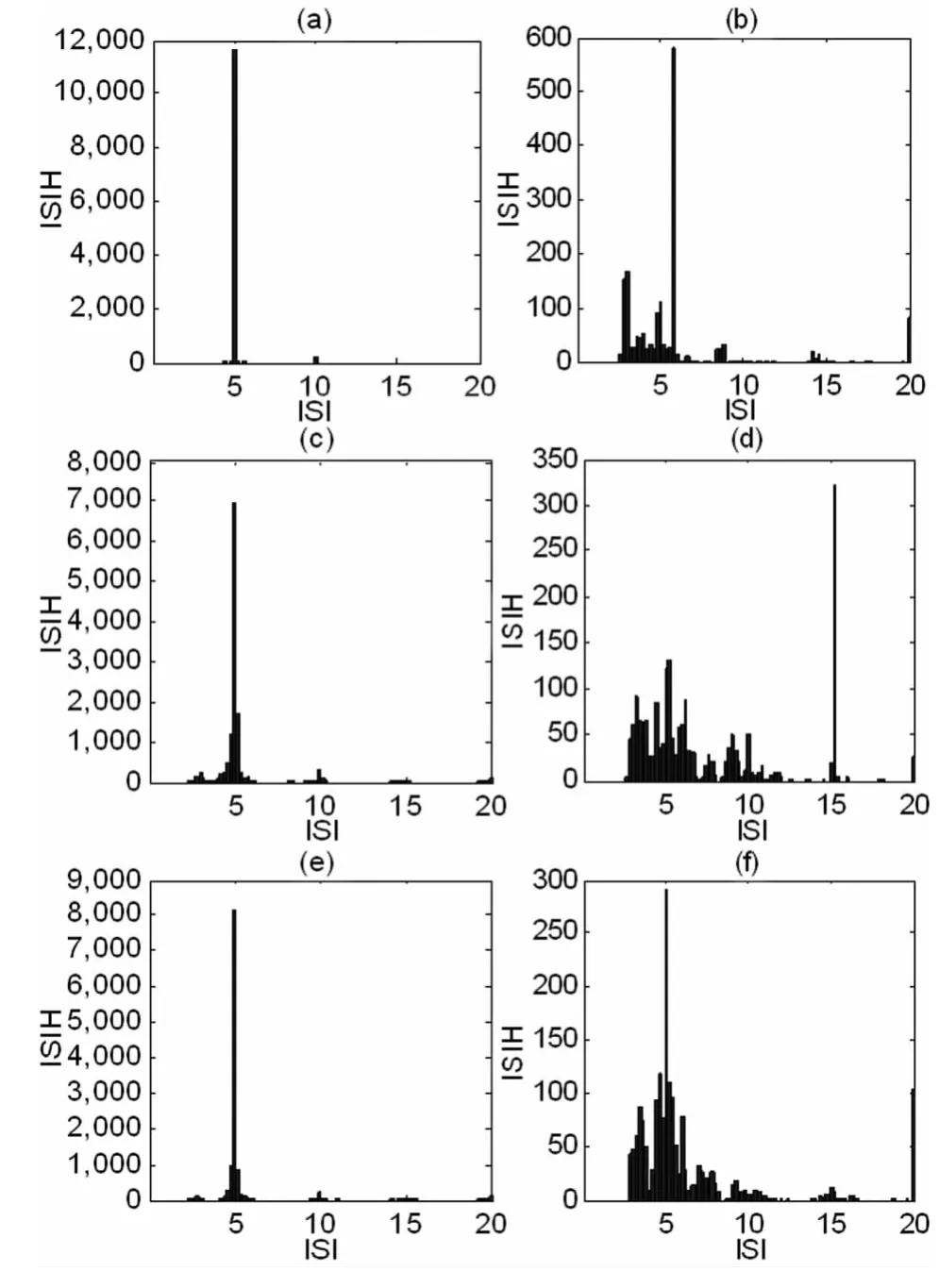
图4 异质性参数σ=0.07、耦合强度g=0.01时不同时滞取值下神经元网络中耦合神经元放电峰峰间期的统计直方图:(a)τ=0;(b)τ=2.5;(c)τ=5.0;(d)τ =7.5;(e)τ=10.0;(f)τ=11.0ig.4 The histogram of interspike intervals of the networks for different τ:(a)τ=0;(b)τ=2.5;(c)τ=5.0;(d)τ=7.5;(e)τ=10.0 and(f)τ=11.0 when σ =0.07 and g=0.01
为了更形象地刻画神经元的放电节律,下面进一步来描绘网络中耦合神经元的放电峰峰间期(ISI).图4(a)、4(c)和 4(e)分别刻画了当τ=0、5.0和10.0时耦合神经元ISI的统计直方图.由图可知,绝大部分神经元的峰峰间期集中在5.0附近.图4(b)、4(d)和 4(f)分别刻画了τ=2.5、7.5和11.0时神经元网络ISI的统计直方图,此时耦合神经元的放电峰峰间期分布在较宽的一个区域上,神经元的放电序列没有明显的规律性.根据以上分析不难得到:耦合时滞对于诱导神经元网络的时空有序行为起着积极的作用,而且时空有序出现在时滞约等于信号周期T=5.0的整数倍时.
接下来,我们也借助于谱放大因子η来定量地刻画耦合时滞对神经元网络共振动力学的影响.当σ=0.07,g=0.01时,图5描绘了谱放大因子η随着时滞τ的变化曲线.由图可知,随着τ的增加,曲线呈现出多峰现象,而且峰值分别出现在τ=0、5.0和10.0处.该结果表明当τ约为信号周期的整数倍时,神经元网络对弱周期信号的响应达到最佳,这与图3和图4的分析结果一致,即:适当的耦合时滞,能够使得参数异质性作用下的共振响应周期性出现,我们也称这种有趣现象为时滞诱导的多重共振.需要指出的是,越来越多的研究关注到耦合时滞对神经元网络动力学中的影响,一些重要结果如时滞增强的同步[27,28]、时滞诱导的同步过渡[29,30]、时滞诱导的多重随机共振[23-25]与相干共振[31]、时滞诱导的时空有序[32]已被揭晓.不同于已有的研究,这里我们研究的是无噪声情形、由不同神经元构成的无标度神经元网络中,耦合时滞对参数异质性作用下网络系统共振动力学的影响.
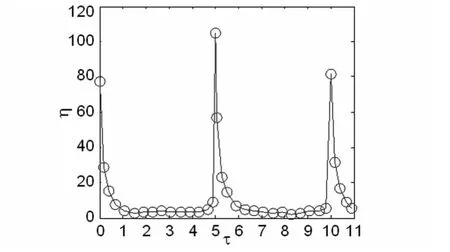
图5 当σ=0.07、g=0.01时谱放大因子η随着时滞τ变化的曲线Fig.5 The dependence of η on when σ =0.07 and g=0.01
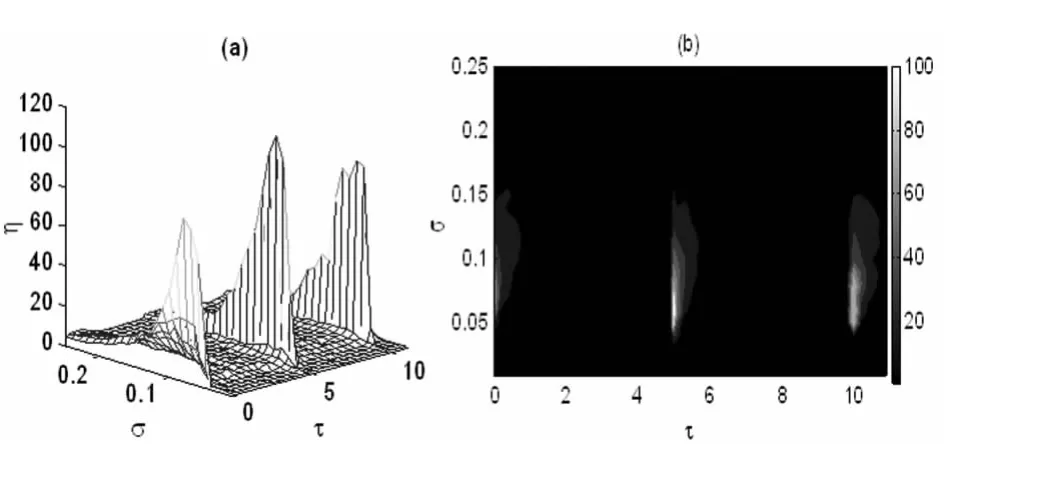
图6 耦合强度为g=0.01时,谱放大因子η随着耦合时滞τ和异质性参数σ变化的图像:(a)曲面图,(b)等高线图Fig.6 The dependence of η on τ and σ when g=0.01:(a)mesh surface,(b)contour plot
进一步数值计算的结果表明,当异质性参数取其它值时,时滞诱导的多重共振也能出现.图6描绘了谱放大因子η随着耦合时滞τ和异质性参数σ变化的曲面图及相应的等高线图.由图可知,对于适中的σ,当τ的取值在0、5.0和10.0附近时,η达到峰值.这表明对于合适的异质性参数,当时滞约为信号周期的整数倍时,即时滞和弱周期信号锁定时,时滞诱导的多重共振也能明显出现.
3 结论
考虑到大脑皮层中一些区域内的神经元网络具有无标度特性,而且参数异质性和时滞在神经系统中普遍存在.鉴于此,本文通过构建节点上动力学不同、含有耦合时滞的无标度神经元网络模型,首次讨论了参数异质性和耦合时滞作用下无标度神经元网络的共振动力学,并得到了一些重要结果:当时滞为零时,适中的参数异质性能够诱导无标度神经元网络的共振响应,而且异质性诱导共振对耦合强度具有鲁棒性;当时滞出现时,在一定的异质性参数范围内,适当的时滞能够诱导多重共振现象,即当时滞约是信号周期的整数倍时,时滞能够使得异质性作用下的共振响应周期性出现.本文的结果丰富了神经科学的理论成果,它对理解神经系统中弱周期信号的探测将提供一定的帮助.
1 Benzi R,Sutera A,Vulpiani A.The mechanism of stochastic resonance.Journal of Physics A,1981,14:L453 ~L457
2 Pikovsky A,Kurths J.Coherence resonance in a noise driven excitable system.Physical Review Letters,1997,78(5):775~778
3 Maritan A,Banavar J R.Chaos,noise,and synchronization.Physical Review Letters,1994,72(10):1451~1454
4 Zhou C S,Kurths J.Noise-induced phase synchronization and synchronization transitions in chaotic oscillators.Physical Review Letters,2002,88(23):230602
5 Van den Broeck C,Parrondo J,Toral R.Noise-induced nonequilibrium phase transition.Physical Review Letters,1994,73(25):3395~3398
6 Gammaitoni L,Hänggi P,Jung P et al..Stochastic resonance.Reviews of Modern Physics,1998,70(1):223 ~287
7 Sagués F,Sancho J M,García- Ojalvo J.Spatiotemporal order out of noise.Reviews of Modern Physics,2007,79(3):829~882
8 Lindner B,García-Ojalvo J,Neiman A et al..Effects of noise in excitable systems.Physics Reports,2004,392:321~424
9 Zhou C S,Kurths J,Hu B.Array- enhanced coherence resonance:Nontrivial effects of heterogeneity and spatial independence of noise.Physical Review Letters,2001,87(9):098101
10 Tessone C J,Mirasso C R,Toral R et al..Diversity-induced resonance.Physical Review Letters,2006,97(19):194101
11 Qi F,Hou Z H,Xin H W.New characterization of disorder taming spatiotemporal chaos.Physics Letters A,2003,308:405~410
12 Glatt E,Gassel M,Kaiser F.Variability-induced transition in a net of neural elements:From oscillatory to excitable behavior.Physical Review E,2006,73(6):066230
13 Li Y Y,Jia B,Gu H G et al..Parameter diversity induced multiple spatial coherence resonances and spiral waves in neuronal network with and without noise.Communications in Theoretical Physics,2012,57(5):817–824
14 Braiman Y,Ditto W L,Wiesenfeld K et al..Disorderenhanced synchronization.Physics Letters A,1995,206:54~60
15 Lafuerza L F,Colet P,Toral R.Nonuniversal Results Induced by Diversity Distribution in Coupled Excitable Systems.Physical Review Letters,2010,105(8):084101
16 Yao C G,Zhan M.Simple electronic circuit model for diversity-induced resonance.Physics Letters A,2010,374:2446~2451
17 Chen H S,Zhang J Q,Liu J Q.Structural-diversity-enhanced cellular ability to detect subthreshold extracellular signals.Physical Review E,2007,75(4):041910
18 Gassel M,Glatt E,Kaiser F.Doubly diversity-induced resonance.Physical Review E,2007,76(1):016203
19 Wu D,Zhu S Q,Luo X Q.Cooperative effects of random time delays and small-world topologies on diversity-induced resonance.Europhysics Letters,2009,86:50002
20 Kandel E R,Schwartz J H,Jessell T M.Principles of neural science.Elsevier,1991
21 Shen C S,Chen H S,Zhang J Q.Amplified signal response by neuronal diversity on complex networks.Chinese Physics Letters,2008,25(5):1591~1594
22 Eguíluz V M,Chialvo D R,Cecchi G A et al..Scale-free brain functional networks.Physical Review Letters,2005,94(1):018102
23 Wang Q Y,Perc M,Duan Z S et al..Delay-induced mutiple stochastic resonances on scale- free neuronal networks.Chaos,2009,19:023112
24 Gan C B,Perc M,Wang Q Y.Delay-aided stochastic mul-tiresonances on scale-free FitzHugh-Nagumo neuronal networks.Chinese Physics B,2010,19(4):040508
25 Yu H T,Wang J,Du J W et al..Effects of time delay on the stochastic resonance in small-world neuronal networks.Chaos,2013,23(1):013128
26 Barabási A L,Albert R.Emergence of scaling in random networks.Science,1999,286:509 ~512
27 Dhamala M,Jirsa V K,Ding M Z.Enhancement of neural synchrony by time delay.Physical Review Letters,2004,92(7):074104
28 张艳娇,李美生,陆启韶.ML神经元的放电模式及时滞对神经元同步的影响.动力学与控制学报,2009,7(1):19 ~23(Zhang Y J,Li M S,Lu Q S.Firing patterns and the effect of time-delay coupling on synchronization of two coupled chaotic ML neurons.Journal of Dynamics and Control,2009,7(1):19~23(in Chinese))
29 Gong Y B,Xie Y H,Lin X et al..Ordering chaos and synchronization transitions by chemical delay and coupling on scale-free neuronal networks.Chaos,Solitons&Fractals,2010,43:96~103
30 Wang Q Y,Chen G R,Perc M.Synchronous bursts on scale-free neuronal networks with attractive and repulsive coupling.PLoS ONE,2011,6(1):e15851
31 Hao Y H,Gong Y B,Lin X et al..Multiple resonances with time delays in scale-free networks of Hodgkin-Huxley neurons subjected to non-Gaussian noise.Science China,2011,54(5):782~787
32 Yang X L,Senthilkumar D V,Kurths J.Impact of connection delays on noise-induced spatiotemporal patterns in neuronal networks.Chaos,2012,22(4):043150
*The project supported by the National Nature Science Foundation of China(11272258,11172342)and the Fundermental Funds Research for the Central Universities(GK201302001)
† Corresponding author E-mail:yangxiaoli@snnu.edu.cn
IMPACT OF DIVERSITY AND DELAYS ON THE RESONANCE DYNAMICS OF NEURONAL NETWORKS*
Jia Yanbing1Yang Xiaoli1†Sun Zhongkui2
(1.College of Mathematics and Information Science,Shaanxi Normal University,Xi’an710062,China)(2.Department of Applied Mathematics,Northwestern Polytechnical University,Xi’an710072,China)
A model of scale-free neuronal networks,which consists of heterogeneous Fitzhugh-Nagumo neurons and time-delayed coupling,was constructed.Then,we explored the nontrivial effects of heterogeneity and time-delayed coupling on the resonance dynamics by numerical simulation in this model.When the delays in the coupling are absent,the result has shown that the response of the neuronal networks to an external subthreshold periodic signal is optimized at an intermediate heterogeneity,namely,an appropriate tuned level of heterogeneity can induce resonance in the neuronal networks.This phenomenon was also confirmed to be robust to the changes of the coupling strength.Most importantly,we find that the delays in the coupling have significant influences on the resonance dynamics.It is revealed that proper delays can induce multiple resonances in the neuronal networks,which appears at each multiple of the oscillation period of the signal.Moreover,the performance of fine tuned delays in inducing multiple resonances can also be clearly observed when the heterogeneity is within an appropriate range.
resonance, diversity, delays, neuronal networks, spectral amplification factor
31 July 2013,
23 September 2013.
10.6052/1672-6553-2013-096
E-mail:yangxiaoli@snnu.edu.cn

