基于变精度粗糙直觉模糊集的决策规则获取

王艳平

(辽宁工业大学理学院，辽宁 锦州 121001)

基于变精度粗糙直觉模糊集的决策规则获取

王艳平

(辽宁工业大学理学院，辽宁 锦州 121001)

以直觉模糊目标信息系统为研究对象，以粗糙集和直觉模糊集为工具，以知识发现为目的，给出了从直觉模糊决策表中获取决策规则的一种有效方法。即通过对Pawlak粗糙隶属函数的定义进行推广，给出粗糙直觉模糊隶属函数，利用新的粗糙隶属函数，建立了变精度粗糙直觉模糊集模型。在此模型基础上定义了变精度粗糙直觉模糊集的近似质量和近似约简，由近似约简导出概率决策规则集，从而给出了直觉模糊决策表的概率决策规则获取方法。最后，以实例说明了这一方法的有效性。

直觉模糊集；变精度粗糙集；近似约简；近似质量；粗糙隶属函数

1 引言

智能信息处理是当前信息科学理论和应用研究中的一个热点领域。由于计算机科学与技术的发展，特别是计算机网络的发展，为人们提供了大量的信息。信息量的不断增长，对信息分析工具的要求也越来越高，人们希望自动地从数据中获取其潜在的知识。作为知识发现的概率分析方法的工具，粗糙集、模糊集等几乎同时产生于20世纪的下半世纪。特别是近20年间，知识发现(规则提取、数据挖掘、机器学习)受到人工智能学界的广泛重视，知识发现的各种不同方法应运而生。文献[1]系统地介绍了各种信息系统上的知识发现与知识约简，包括模糊信息系统、随机信息系统、格值信息系统等；文献[2]在模糊相似关系下给出了一种基于直觉模糊粗糙集的知识获取方法。但是，对于决策目标为直觉模糊集的直觉模糊信息系统的知识发现和知识约简[3]的研究还较少。特别是将变精度粗糙集模型[4,5]推广到直觉模糊环境下，解决直觉模糊环境下带有噪声的数据分类问题，还未见相关文献。因此，本文将变精度粗糙集与直觉模糊集融合建模，用于直觉模糊决策信息系统的知识获取。对于直觉模糊决策表，通过用(a,b)—截集[6]将输出直觉模糊集转化为普通集合，定义了新的粗糙隶属函数，它是Pawlak粗糙隶属函数[7]的进一步推广；并通过设定置信阈值(α,β)建立变精度粗糙直觉模糊集模型；应用所建立的变精度粗糙直觉模糊集模型，给出直觉模糊决策表的近似约简和概率决策规则；从而解决了直觉模糊目标信息系统的知识获取问题。

2 直觉模糊集的基本理论

定义1[8](直觉模糊集)设U是一个非空经典集合，称U上形如X={〈x,μX(x),νX(x)〉|x∈U}的三元组为U上的一个直觉模糊集。其中，函数μX：U→[0,1]和νX：U→[0,1]，并且满足0≤μX(x)+νX(x)≤1，∀x∈U。简记为X=(μX(x),νX(x))。记U上所有直觉模糊集构成的集合为IF(U)。称(μX(x),νX(x))为直觉模糊数。

定义2[9]对直觉模糊数规定序如下：

(μX(x),νX(x))≥(μX(y),νX(y))当且仅当μX(x)≥μX(y)且νX(x)≤νX(y)，∀x,y∈U。

定义3[6](直觉模糊集的截集) 令X∈IF(U)，I={(a,b)|a,b∈[0,1],a+b≤1}，对∀(a,b)∈I， 则称X(a,b)={x∈U|μX(x)≥a,νX(x)≤b}为直觉模糊集X的(a,b)—截集。

3 变精度粗糙直觉模糊集

定义4 设IFS=(U,A,V,f)是一个决策表，其中，A=C∪D，C∩D=∅，C为条件属性，D为决策属性，R是有限非空论域U上的等价关系，IFX∈IF(U)为输出集合，则将这样的决策表称为粗糙直觉模糊决策表。

由于直觉模糊集合IFX的(a,b)—截集为普通集合，对于输出直觉模糊集IFX∈IF(U)中的任意一个普通集合IFX(a,b)，可以应用粗糙隶属函数，将IFX(a,b)的粗糙隶属函数定义为:

νIFX(a,b)(x)=

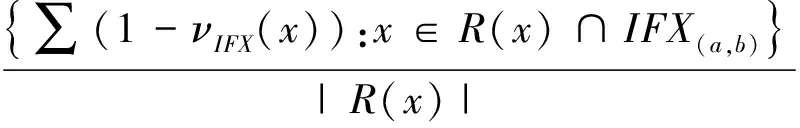
其中,R(x)表示x所在的R等价类，|R(x)|表示等价类的基数。μIFX(a,b)(x)表示x属于集合IFX(a,b)的程度，它等于R(x)∩IFX(a,b)中所包含元素的隶属度之和与|R(x)|的商；νIFX(a,b)(x)表示x不属于集合IFX(a,b)的程度，它等于1减去R(x)∩IFX(a,b)中所包含元素的可能度之和与|R(x)|的商。

由定义4可知，在同一R等价类中的x，具有相同的粗糙隶属函数值。

定理1 对于粗糙直觉模糊决策表IFS=(U,A,V,f)中的任意一个输出子集IFX(a,b)⊆U，有:

0≤μIFX(a,b)(x)≤1，0≤νIFX(a,b)(x)≤1，且0≤μIFX(a,b)(x)+νIFX(a,b)(x)≤1。

证明 因为0≤μIFX(x)≤1，0≤νIFX(x)≤1，且R(x)∩IFX(a,b)⊆R(x)，所以，0≤μIFX(a,b)(x)≤1，0≤νIFX(a,b)(x)≤1成立。又因为0≤μIFX(x)+νIFX(x)≤1，所以，0≤μIFX(a,b)(x)+νIFX(a,b)(x)=1-(∑(1-μIFX(x)-νIFX(x)):x∈R(x)∩IFX(a,b))/|R(x)|≤1。

□

由定理1可知，IFX(a,b)的粗糙隶属函数(μIFX(a,b)(x),νIFX(a,b)(x))仍是一个直觉模糊数。

定义5 (变精度粗糙直觉模糊集)令置信度0.5<α<1-β≤1，P⊆C，则将直觉模糊集IFX∈IF(U)基于(a,b)—截集的(α,β)上、下近似定义为:

∪{x∈U|(μIFX(a,b)(x),νIFX(a,b)(x))≥(α,β)}

∪{x∈U|(μIFX(a,b)(x),νIFX(a,b)(x))>(β,α)}

特别地，当(α,β)=(1,0)，输出集合IFX清晰时，变精度直觉模糊粗糙集模型退化为粗糙集模型。

4 直觉模糊决策表的概率规则获取

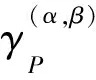
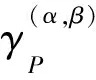
称为(C,D)的概率规则，置信度为(α,β)，表示为{rij}。其中，Ci为条件类，IFXj为决策类。

综上可得，从直觉模糊决策表获取概率决策规则的基本步骤为：

(1)根据条件属性和决策属性对论域进行分类；

(2)计算每个决策类的粗糙隶属函数；

(3)设定置信阈值，求出每个决策类的下近似；

(4)求出全部条件属性集C的分类质量；

(5)求出直觉模糊决策目标信息系统的约简；

(6)给出概率决策规则集。

下面通过一个实例来说明直觉模糊决策表的概率决策规则获取方法。本文以文献[10]中的数据为基础，作了适当修改，将决策集改为直觉模糊集，可由管理者投票给出。

例1 设有12个运输方案，每个运输方案包括四个条件属性，条件属性集C={c1,c2,c3,c4}，一个决策属性，决策属性集D={d}。其中，c1为运输成本，c2为批量规模，c3为库存量成本，c4为反应时间。d为运输方案评价，其中，d1表示运输方案评价差，d2表示运输方案评价好。若决策是清晰的，则可将一个评价级别设置为1，另一个设置为0，但目前决策者无法作出清晰判断，管理者给出的决策是直觉模糊的。具体数据见表1和表2。

根据条件属性C对论域进行划分，可得如下等价类：

U/C={X1,X2,X3,X4,X5,X6}

其中，X1={x1}，X2={x2,x3}，X3={x4}，X4={x5}，X5={x6,x7,x8,x10,x11,x12}，X6={x9}。

按决策属性D对论域U进行划分，可得如下决策类:

U/D={IFB,IFG}

其中，IFB={x1,x4,x5,x8,x9}，IFG={x2,x3,x6,x7,x10,x11,x12}。

令a=min{μ1(x),μ2(x),…,μt(x)}，b=max{ν1(x),ν2(x),…,νt(x)}，其中t为某决策类包含的元素个数。计算每个决策类IFX(a,b)的粗糙隶属函数得：

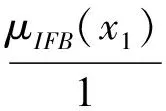
νIFB(a,b)(x)=

类似可求得其它隶属函数值，见表3。

令置信阈值(α,β)=(0.7,0.29)， 可得:

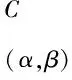
νIFB(a,b)(x))≥(α,β)}=X1∪X6

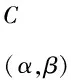
νIFG(a,b)(x))≥(α,β)}=X2∪X5

Table 1 Decision of transport scheme

求得全部条件属性集C的分类质量为:

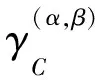
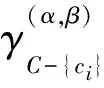
Table 2 Intuitionistic fuzzy partition on scheme of managers

Table 3 Rough membership function values of decision classes

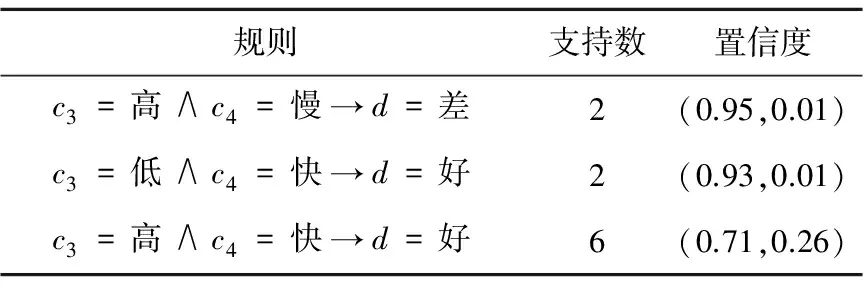
Table 4 Probability decision rule sets

通过实例表明本文给出的决策方法有效可行而且计算简单，易于实现。如果记条件属性的个数为m、条件类的个数为p，则算法的时间复杂度为O(mp)。该方法有效地推广了粗糙隶属函数在变精度粗糙直觉模糊集模型构建以及直觉模糊信息系统决策问题中的应用。

5 结束语

本文针对带有噪声的直觉模糊决策信息系统，推广了粗糙隶属函数，在Pawlak的粗糙隶属函数基础上增加了非隶属度的计算，构建了变精度粗糙直觉模糊集模型，并将该模型用于粗糙直觉模糊决策表的概率决策分析。该方法能够在决策者的思维存在模糊性和数据存在噪声的情况下，获取强的概率决策规则。

[1] Zhang W X,Liang Y,Wu W Z.Information system and knowledge discovery[M]. Beijing:Science Press, 2003.(in Chinese)

[2] Fan L, Lei Y J. Knowledge acquisition method of intuitionistic fuzzy rough sets [J].Computer Engineering and Applications, 2008,44(4):39-41.(in Chinese)

[3] Lu Y L, Lei Y J, Hua J X．Attribute reduction based on intuitionistic fuzzy rough set [J]. Control and Decision, 2009,24(3):335-341.(in Chinese)

[4] Mieszkowicz R A, Rolka L. Variable precision fuzzy rough sets [J]. Transactions on Rough Sets I, 2004,3100:144-160.

[5] Li F, Liu Q H，Yang G W. Definition of variable precision fuzzy rough sets [J]. Control and Decision,2008,23(11):1206-1210.(in Chinese)

[6] Li M. Cut sets of intuitionistic fuzzy sets [J]. Journal of Liaoning Normal University, 2007,30(2):152-154.(in Chinese)

[7] Pawlak Z, Skowron A. Rough membership functions[M]∥Advances in Dempster-Shafer Theory of Evidence,1994:251-271.

[8] Atanassov K.Intuitionstic fuzzy sets[J]. Fuzzy Sets and Systems, 1986,20(2):87-96．

[9] Chen S M, Tan J M. Handling multicriteria fuzzy decision-making problems based on vague set theory[J]. Fuzzy Sets and Systems, 1994,67(2):163-172.

[10] Jian L R. Hybrid rough set method and its application facing uncertainty decision-making [M]. Beijing:Science Press,2008.(in Chinese)

附中文参考文献：

[1] 张文修, 梁怡, 吴伟志. 信息系统与知识发现[M]. 北京:科学出版社,2003.

[2] 樊雷, 雷英杰. 基于直觉模糊粗糙集的一种知识获取方法[J].计算机工程与应用,2008,44(4):39-41.

[3] 陆艳丽, 雷英杰, 华继学．基于直觉模糊粗糙集的属性约简[J]. 控制与决策, 2009,24(3):335-341.

[5] 李凡, 刘启和，杨国纬. 变精度模糊粗糙集的一种定义[J]. 控制与决策,2008,23(11):1206-1210.

[6] 李敏. 直觉模糊集的截集[J]. 辽宁师范大学学报,2007,30(2):152-154.

[10] 菅利荣. 面向不确定性决策的杂合粗糙集方法及其应用[M]. 北京:科学出版社,2008.

WANG Yan-ping,born in 1965,professor,her research interests include fuzzy set theory and rough set theory.

Decision rule acquisition based on variable precision rough intuitionistic fuzzy sets

WANG Yan-ping
(School of Science,Liaoning University of Technology,Jinzhou 121001,China)

Taking the intuitionistic fuzzy goal information system as the research object, rough set and intuitionistic fuzzy sets as the research tools, knowledge discovery as the research purpose, an effective method is given to get decision rules from the intuitionistic fuzzy decision table. That is, through generalizing the definition of Pawlak rough membership functions, the rough intuitionistic fuzzy membership function is given, and using new rough membership function, a variable precision rough intuitionistic fuzzy set model is established. And based on this model, the approximation quality and approximate reduction of the variable precision rough intuitionistic fuzzy set are defined, the approximate reduction derives the probabilistic decision rules set, hence the probabilistic decision rules of the intuitionistic fuzzy decision table acquisition method is given. Finally, the practical example is given to illustrate the effectiveness of the method.

intuitionistic fuzzy sets；variable precision rough sets;approximation reduction；approximate quality;rough membership function

2012-08-14;

2012-12-27

辽宁省教育厅基金资助项目(L2012226)

1007-130X(2014)03-0541-04

TP301;O236

A

10.3969/j.issn.1007-130X.2014.03.029

王艳平(1965-),女,辽宁锦州人，教授，研究方向为模糊集理论与粗糙集理论。E-mail:Weiyanping65@yahoo.com.cn

通信地址：121001 辽宁省锦州市辽宁工业大学理学院

Address:School of Science,Liaoning University of Technology,Jinzhou 121001,Liaoning,P.R.China