基于约束投影的近邻传播聚类算法
钱雪忠,赵建芳,贾志伟
(1.江南大学物联网工程学院,江苏 无锡 214122;2.成都信息工程学院,四川 成都 610225)
基于约束投影的近邻传播聚类算法
钱雪忠1,赵建芳1,贾志伟2
(1.江南大学物联网工程学院,江苏 无锡 214122;2.成都信息工程学院,四川 成都 610225)
提出了一种基于约束投影的近邻传播AP聚类算法。AP算法是在数据点相似度矩阵的基础上进行聚类的,很多传统的聚类方法都无法与其相媲美。但是,对于结构复杂的数据,AP算法往往得不到理想的结果。文中算法先对约束信息进行扩展,然后利用扩展的约束信息指导投影矩阵的获取,在低维空间中,利用约束信息对聚类结果进行修正。实验表明,文中算法与对比算法相比,时间性能更优,聚类效果更佳。
半监督;聚类;约束信息;投影;近邻传播
1 引言
将物理或抽象对象的集合分成由类似的对象组成的多个类的过程称为聚类。聚类算法是在没有任何先验信息的情况下进行的,因此这类方法又称为无监督学习方法。然而,在很多实际问题中,有时候我们可以获得少部分的先验信息,如何利用先验信息来改善聚类算法的性能成为一个新的研究热点,所提出的算法称为半监督聚类算法[1]。通常先验信息是由领域专家给出的,先验信息可分为类标记信息和成对约束信息。类标记信息明确了某数据点应属于的类,而成对约束信息则规定了某两个数据点之间的联系,若它们应属于同一个类,则称这两个数据点之间存在正约束关系(Must-link),反之,则称它们存在负约束关系(Cannot-link)。半监督聚类算法大致可分为两类,一类是基于约束的方法,另一类是基于距离的方法。前者利用成对约束先验信息来指导最优聚类的搜索过程。如司文武、钱江涛等人在文献[2]中提出了一种基于谱聚类的半监督聚类算法。该方法利用标签数据信息,调整点与点之间形成的相似度矩阵,最后基于被调整的聚类矩阵进行谱聚类。而在文献[3]中,赵凤和焦李成等人提出了利用先验信息来寻找能够体现数据结构的特征向量组合,并且在UCI数据集和MINIST手写数据集上验证了算法的有效性和鲁棒性。后者则是利用先验信息来训练相似性距离测度函数,使之尽量满足所给的先验信息,再使用基于距离的方法来聚类。如Xing E P等人[4]提出利用标识信息并基于凸的方法优化了的马氏距离。Klein D等人[5]提出利用标记信息并基于图的方法改进了欧式距离。而Li Tao等人[6]充分利用先验信息所隐藏的信息,提出了基于特征向量的空间映射及矩阵因数分解的方法。然而,同时集成约束和聚类的方法也受到了研究者的关注。如Bilenko M等人[7]通过把距离约束转化为距离度量,改进了K-means算法,并将上述两种思想集成于一个框架之下。Basu S等人[8]提出了一种统一的半监督聚类概率模型,利用改进后的隐式空间数据间的距离反映约束关系。
本文所提出的基于约束投影的近邻传播聚类算法属于基于约束的方法。近邻传播聚类算法APC(Affinity Propagation Clustering)[9]是Frey B J在《Science》中提出来的。与以往的聚类方法相比,该方法可更快地处理大规模数据,得到更好的聚类效果。文中作者将近邻传播算法应用在人脸图像聚类、基因表达数据的基因识别、手写体字符识别、最优航空路线确定等问题上,实验结果表明,近邻传播聚类算法在很短的时间内就能得到K中心算法花费很长时间才能达到的聚类效果。近邻传播算法的应用范围比以往的聚类算法更广,这是因为它对样本点间形成的相似度矩阵的对称性没有任何要求。然而对于本身具有复杂结构的数据集,近邻传播算法也不能得到合理的效果[10]。针对近邻传播算法的这一缺陷,本文在半监督近邻传播算法的基础上进一步利用先验信息,使得先验信息的应用提前到降维过程中。在降维过程中应用先验信息一方面能约简数据集,使得近邻传播算法更好地发挥其性能;另一方面使约简后的数据集最大程度上保留原数据集的信息。实验结果表明,基于约束投影的近邻传播聚类算法能很好地弥补近邻传播算法处理复杂数据效果不佳的缺陷,在时间性能和聚类结果方面都能取得较为满意的效果。
2 AP算法及SAP算法
2.1 AP算法
近邻传播算法的目的是找到最优类代表点集合(Exemplar),使得所有数据点到最近的类代表点的相似度之和最大。AP算法是在数据点的相似度矩阵S(Similarity)上进行聚类的。由于聚类的目标是使数据点与其类代表点之间的距离最小化,所以任意两点的相似度可定义为两点距离平方的相反数。
AP算法引入两个重要的信息量参数,分别为吸引度R(Responsibility)和归属度A(Availability)。R(i,k)从点xi指向xk,表示xk适合作为数据点xi的聚类中心程度。A(i,k)是从点xk指向xi,表示点xi选择点xk作为其聚类中心的程度。AP算法的迭代过程是不断更新每一个点的吸引度和归属度的过程,迭代过程直到产生高质量的Exemplar结束。R和A的更新公式如下:
R(i,k)=S(i,k)-max{A(i,j)+S(i,j)}
(j∈{1,2,…,N,且j≠k})
(1)
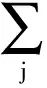
(j∈{1,2,…,N,且j≠i,j≠k})
(2)
R(k,k)=p(k)-max{A(k,j)+S(k,j)}
(j∈{1,2,…,N,且j≠k}
(3)
第i次迭代后,吸引度Ri和归属度Ai要与前一次的Ri-1和Ai-1进行加权更新,更新公式如下:
Ri=(1-lam)*Ri+lam*Ri-1
(4)
Ai=(1-lam)*Ai+lam*Ai-1
(5)
其中,lam∈[0.5,1)。
2.2SAP算法
SAP算法是利用先验信息来调整点与点之间的相似度矩阵,从而形成新的相似度矩阵S,在新得到的相似度矩阵的基础上进行AP算法[11]。算法根据所给的先验信息对相似度矩阵进行初步调整。当两个数据点属于正约束集,即(xi,xj)∈M时,认为这两个数据点之间有很高的相似度,调整相似度矩阵,令S(i,j)=0;当两个数据点属于负约束集,即(xi,xj)∈C,认为这两个数据点相似度极低,则调整相似度矩阵,令S(i,j)=-∞。在初步调整之后,算法又基于最短路径原则对不包含在先验信息中的数据点的相似度进行了全局调整。调整方法为:如果某对数据点既不在正约束集M中,又不在负约束集C中,但存在第三个数据点与这对数据点中两个数据点分别相连,并且这一数据点与这两个数据点的相似度之和大于这对数据点的初始相似度,则调整这对数据点的相似度为较大的相似度。最后利用C集中的信息对上述调整进行修正。上述过程转化成公式为:
若(xi,xj)∈M,则:
S(i,j)=S(j,i)=0
(6)
若(xi,xj)∈C,则:
S(i,j)=S(j,i)=-∞
(7)
若(xi,xj)∉{M∪C},则:
S(i,j)=S(j,i)=
max{S(i,j),S(i,k)+S(k,j)}
(8)
若(xi,xj)∉{M∪C}&(xi,xk)∈C&(xk,xj)∈M,则:
S(i,j)=S(j,i)=-∞
(9)
虽然AP算法对相似度矩阵的对称性没有要求,能在很短的时间内得到K-means算法花费很长时间才能得到的聚类效果,但是对于结构复杂的数据集,其处理时间很长,且不能得到理想的聚类结果。SAP算法在AP算法的基础上加入先验信息,在一定程度上提高了AP算法的性能,但是其时间性能却还是有待改善。据此提出了基于约束投影的近邻传播聚类算法。
3 基于约束投影的近邻传播聚类算法
3.1 约束投影
首先对先验信息做如下规定:若数据点xi和xj在聚类后属于同一个类,则称(xi,xj)是一个正约束对;若数据点xi和xj在聚类后不能属于同一个类,则称(xi,xj)是一个负约束对,所有正约束对的集合称为正约束集M,所有负约束对的集合称为负约束集C。根据约束传播理论可知,如果(xi,xj)∈M,且(xj,xk)∈M,则可以得到(xi,xk)∈M;如果(xi,xj)∈C,且(xj,xk)∈M,则可以得到(xi,xk)∈C。根据上述约束传播,可以得到更多的约束,更新正约束集M和负约束集C,得到扩充的约束集M和C。
数据投影是根据某一准则,将高维数据变换到有意义的低维表示[12]。在利用约束信息指导投影矩阵的获取时,除了考虑根据约束传播原理更新的约束集M和C以外,还需考虑以下问题:在一个很小的局部区域内的数据点应该具有相似的特性,在高维空间中离正约束对最近的一对数据点,如果不属于负约束集,在低维空间中应尽量使其靠近。同理可得,离负约束对最近的一对数据点,如果不属于正约束集,在低维空间中应尽量使其远离。为了解决上述问题,我们分别建立临时正约束集M′和临时负约束集C′,对M集和C集做临时的扩充。这里所说的临时扩充是指这一步扩充所得的约束信息仅用于指导投影矩阵的获取,而在低维空间中进行聚类时,使用的监督信息是根据约束传播原理所得到的M集和C集。M′和C′的计算方法如下:
∀xl∈Nk(xi),若dist(xi,xj)≥dist(xl,xj),且M(xl)∩C(xj)=∅,C(xl)∩M(xj)=∅,则M′=M∪{(xl,xj)};
∀xl∈Nk(xi),若dist(xi,xj)≤dist(xl,xj),且M(xl)∩M(xj)=∅,则令C′=C∪{(xl,xj)}。
其中,Nk(xi)表示xi的k最邻近集,dist(xi,xj)表示数据点xi和数据点xj之间的欧氏距离,M(xi)、C(xi)分别表示与数据点xi有正约束关系和负约束关系的所有数据点的集合。
为了在投影时充分利用M′和C′所包含的信息,我们对M′和C′所包含的信息进行了量化,量化的目标是使得M′中的数据点投影到低维空间中的距离尽量缩小,而C′中的数据点投影到低维空间中的距离尽量拉大,量化过程如下:
(10)
其中,λ是伸缩因子,用于控制信息量的放大与缩小程度。dist(xi,xj)是数据点xi与数据点xj之间的欧氏距离。
为求得投影矩阵,构造目标函数f(W):
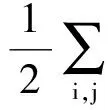
(11)
展开整理得:
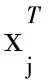
WT(XDXT-XGXT)W=
WTX(D-G)XTW
(12)
其中,D是对角矩阵,Dii=∑jgi,j。为求得最大值,构造拉格朗日函数并且对ωi求导,投影矩阵W由矩阵D-G的前k个最大特征向量组成。
3.2 算法执行过程
基于约束投影的近邻传播聚类算法CBPAP(Constraints Based Projection Affinity Propagation) 对约束信息进行了两次扩展,第一次扩展是基于约束传播进行的,旨在从逻辑的角度扩大约束信息集,也可称为真扩展。第二次扩展的目的是为了数据投影后能更准确地反映其原有的特性。第二次扩展是基于最小邻域进行的,由于本次扩展生成的约束集并不用于低维空间中的聚类,因此称为临时扩展。将临时扩展所得到的约束进行量化,并用于指导投影矩阵的获取。在低维空间中,参照SAP算法的执行过程,对相似度矩阵进行修改,在修改后的相似度矩阵上进行迭代求解。与SAP算法不同的是,CBPAP算法在修改相似度矩阵时使用第一次扩展所产生的约束信息,而利用第二次扩展所产生的约束信息对聚类结果进行调整,这样做的目的是为了使聚类结果既满足约束信息的要求,又符合某一邻域内的数据点具有相似特性的观点。具体做法是查看聚类结果,若聚类结果中有数据点违反了M′中的约束信息,则分别计算这两个数据点到其聚类中心的距离,调整这两个数据点到距离较小的数据点所在的类中;若聚类结果中有数据点违反了C′中的约束信息,计算这两个数据点到所有类的聚类中心的距离,在不违反C′约束信息的情况下,分别调整这两个数据点到离其聚类中心距离最小的类中。CBPAP算法的执行过程如下:
(1)基于约束传播对正约束集M和负约束集C进行第一次扩展。若(xi,xj)∈M,(xj,xk)∈M,则M=M+(xi,xk);若(xi,xj)∈C,(xj,xk)∈M,则C=C+(xi,xk)。
(2)计算临时约束集M′和C′,并根据gi,j的计算方法量化M′和C′中的信息。对于任意(xi,xj)属于M′或C′,分别计算xi、xj的k近邻集Nk(xi)、Nk(xj),∀xl∈Nk(xi),若dist(xi,xj)≥dist(xl,xj),且Ml∩Cj=∅,Cl∩Mj=∅,则令M′=M∪{(xl,xj)};若(xi,xj)∈C,分别计算xi、xj的k近邻集Nk(xi)、Nk(xj),∀xl∈Nk(xi),若dist(xi,xj)≤dist(xl,xj),且Ml∩Mj=∅,则令C′=C∪{(xl,xj)}。根据gi,j的计算方法量化M′和C′中的信息。
(3)利用量化的信息指导投影矩阵W的获取,并将原数据点空间X={x1,…,xn}⊂Rd投影到空间Y={y1,…,yn}⊂Rk。
(4)调整相似度矩阵S。若(yi,yj)∈M,调整S(i,j)=0。
(5)基于最短路径原则进行全面调整。如果(yi,yj)∉{M∪C},则S(i,j)=max{S(i,j),S(i,k)+S(k,j)}。
(6)利用C集对上述两步的调整进行修正。若(yi,yj)∉{M∪C}并且(yi,yk)∈C、(yk,yj)∈M,则S(i,j)=-∞,S(j,i)=-∞。
(7)在调整后的相似性矩阵上迭代计算R(i,k)和A(i,k),直到产生最优Exemplar或者达到最大迭代次数为止。
(8)利用临时约束信息对聚类结果进行调整。
4 实验及结果
本实验在UCI数据集上进行,他们分别是Iris、Balance、Austra、Ionosphere和Air,表1对这些数据集的相关特性进行了描述。

Table 1 Information of dataset UCI
约束信息通常是由邻域专家标记产生的,实验中,为了避免人为标记带来的偶然性,我们对数据点进行编号,每次随机产生一组数字,如果这组数字对应的编号所代表的数据点在同一个类中,则将这两个数据点组成一组正约束对加入正约束集中,否则组成负约束对加入负约束集中。实验输出的结果是100次实验的平均值。在这100次实验中,每次实验都随机产生新的约束对。实验利用监督信息,将三组数据集都降到了三维空间。实验所用的机器为Intel Core2 Duo CPU,2.0 GHz,内存为1.00 GB。
首先本文设计了验证算法时间性能的实验,表2列出了AP算法在各数据集上的运行时间,表3列出了约束为5、10、15和20的情况下SAP算法和CBPAP算法的时间性能对比,时间的单位为s。

Table 2 Time of AP
由表2可以看出,随着维数的增多,AP算法的运行时间变长,换言之,AP算法对于高维数据的处理效果是不理想的。由表3可以看出,CBPAP算法的时间性能明显优于SAP算法。综合表2和表3,SAP算法和CBPAP较AP算法都有所提高,且CBPAP提高的程度比SAP算法要高。
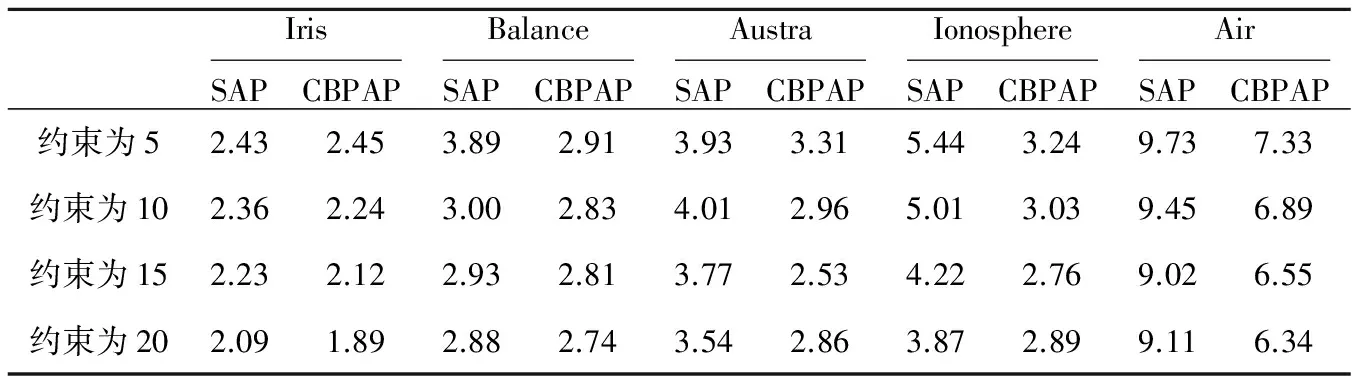
Table 3 Contrast of time between SAP and CBPAP
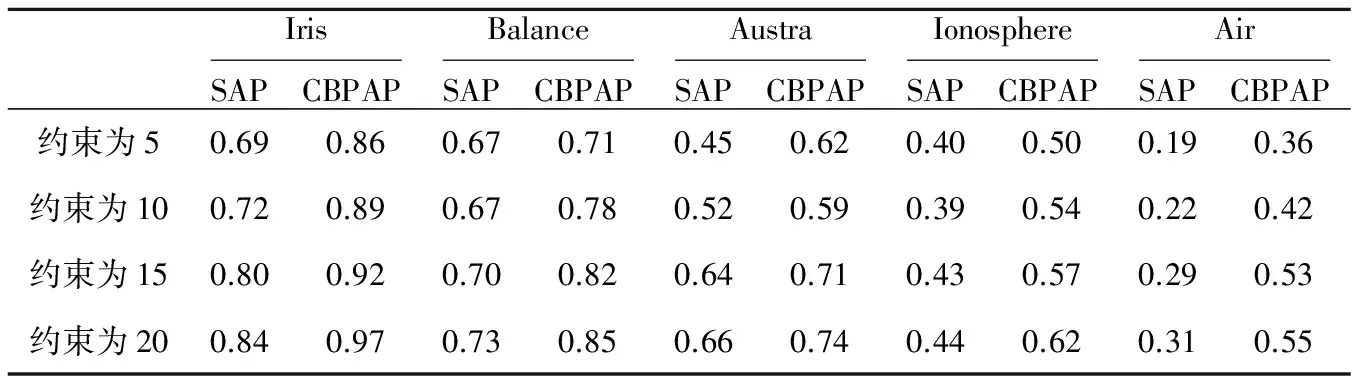
Table 4 Output of average CRI
除了上述验证算法聚类效果的实验以外,本文还采用CRI指标对两类半监督的AP算法的聚类效果进行对比。
CRI指标被视为常用的半监督聚类评价指标[5],其定义如下:
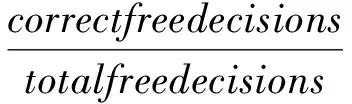
(13)
其中,totalfreedecisions=n(n-1)/2-Cn,n为数据点的数目,Cn表示约束对的数目。correctfreedecisions表示划分正确的数据对的数目减去约束对中划分正确的数据对的数目。对于相同数量的约束对进行100次实验,并输出其平均结果。表4为实验结果输出的平均CRI值。
由表4可以看出,在约束对数目相同的情况下,CBPAP算法的聚类效果显然优于SAP算法。而CBPAP算法在处理样本数较多的Balance数据集和特征数较多的Ionosphere数据集时所表现出的优越性就更为突出了。产生这种优势的原因是由两方面组成的:第一,在利用监督信息进行约束投影的时候对约束信息进行了两次扩展,这两次扩展既考虑了逻辑上的正确性又顾及了数据的空间特性,所求得的投影空间能在约简数据空间的同时更好地保留原数据集的特性,这样的处理方式能有效地解决AP算法处理复杂数据集时效果不理想的弊端;第二,在聚类结束后利用临时约束信息对聚类结果进行了修正,这样能进一步提高聚类效果。
5 结束语
本文提出了基于约束投影的近邻传播聚类算法。该方法在整个聚类过程中多次使用了约束信息,能充分挖掘和利用约束信息指导聚类。文中两次扩展了约束信息,逻辑扩展在保证约束信息正确的情况下增大了约束信息集,而临时扩充符合数据点的空间特性,为数据集的投影和最后聚类修正提供保证。实验结果表明,文中所提出的方法能很好地解决AP算法处理复杂数据集性能不佳的弊端,为半监督AP算法的研究提供了一种新思路。然而,本文在第二次扩展约束信息集的时候不能完全保证约束信息的正确性,这对于后来的聚类效果是有影响的,并且在进行降维时所选择的降维空间数是一个经验值,不能很好地从理论方面解释怎样的空间维数是最合适的。因此,如何结合数据集本身的特性来扩展约束信息并选取合适的降维空间,将是下一步的研究方向。
[1] Zhu Xiao-jin.Semi-supervised learning literature survey[R]. Computer Science TR 1530, Wl:University of Wisconsin:Department of Computer Sciences,2008.
[2] Si Wen-wu, Qian Jiang-tao.Semi-supervised clustering based on spectral clustering[J].Computer Applications, 2005,26(6):1347-1349.(in Chinese)
[3] Zhao Feng, Jiao Li-cheng, Liu Han-qiang,et al. Semi-supervised eigenvector selection for spectral clustering[J]. Pattern Recognition and Artificial Intelligence,2011,24(1):48-55.(in Chinese)
[4] Xing E P, Ng A Y, Michael I, et al. Distance metric learning with application to clustering with side-information[C]∥Advances in Neural Information Processing Systerm,2003:505-512.
[5] Klein D, Kamver S D. From instance-level constraints to space-level constraints:Making the most of prior knowledge in data clustering[C]∥Proc of ICML’02, 2002:307-314.
[6] Ding C,Li Tao,Peng Wei.On the equivalence between non-negative matrix factorization and probabilistic latent semantic indexing[J].Computational Statistics and Data Analysis,2008, 52(8):3913-3927.
[7] Bilenko M,Basu S,Mooney R J.Integrating constraints and metric learning in semi-supervised clustering[C]∥Proc of ICML’04, 2004:11.
[8] Basu S,Banerjee A,Mooney R J.Semi-supervised clustering by seeding[C]∥Proc of the 19th International Conference on Machine Learning, 2002:27-34.
[9] Frey B J,Dueck D.Clustering by passing messages between data points[J].Science,2007,315(5814):972-976.
[10] Yuan Li-yong, Wang Ji-yi.An improved semi-supervised K-means clustering algorithm[J].Computer Engineering & Science,2011,33(6):138-143.(in Chinese)
[11] Xiao Yu, Yu Jian. Semi-supervised clustering based on affinity propagation algorithm[J].Journal of Software,2008,19(11):2803-2813.(in Chinese)
[12] An S, Liu W, Venkatesh S. Exploiting side information in locality preserving projection[C]∥Proc of Conference on Computer Vision and Pattern Recognition (CVPR), 2008:1-8.
附中文参考文献:
[2] 司文武,钱江涛.一种基于谱聚类的半监督聚类方法[J].计算机应用,2005,26(6):1347-1349.
[3] 赵凤,焦李成,刘汉强,等.半监督谱聚类特征向量选择算法[J].模式识别与人工智能,2011,24(1):48-55.
[10] 袁利永,王基一.一种改进的半监督K-means聚类算法[J].计算机工程与科学,2011,33(6):138-143.
[11] 肖宇,于剑.基于近邻传播算法的半监督聚类[J].软件学报,2008,19(11):2803-2813.
QIAN Xue-zhong,born in 1967,MS,associate professor,his research interests include database technology, data mining, and network security.

赵建芳(1988-),女,江苏张家港人,硕士生,研究方向为数据挖掘。E-mail:Zhao_jian_fang@foxmail.com
ZHAO Jian-fang,born in 1988,MS candidate,her research interest includes data mining.

贾志伟(1988-),男,江苏连云港人,硕士生,研究方向为数据挖掘。E-mail:441065471@qq.com
JIA Zhi-wei,born in 1988,MS candidate,his research interest includes data mining.
Constraint projection based affinity propagation
QIAN Xue-zhong1,ZHAO Jian-fang1,JIA Zhi-wei2
(1.School of Internet of Things Engineering,Jiangnan University,Wuxi 214122;2.Chengdu University of Information Technology,Chengdu 610225,China)
A clustering algorithm, named constraint projection based affinity propagation (AP), is proposed. The AP algorithm conducts clustering based on similarity matrix, outperforming many traditional clustering algorithms. However, for those datasets with complex structure, the AP algorithm cannot always achieve the ideal results. Firstly, constraints are enlarged. Secondly, the enlarged constrains are used in getting the projection matrix. At last, the clustering result is updated by the enlarged constraints in the space with lower dimension. The result shows that, compared with the comparison algorithms, the proposal is better in both time performance and clustering results.
semi-supervised;clustering;constraints;projection;affinity propagation
2012-09-04;
2012-12-21
国家自然科学基金资助项目(61103129);江苏省科技支撑计划资助项目(BE2009009)
1007-130X(2014)03-0524-06
TP274
A
10.3969/j.issn.1007-130X.2014.03.026

钱雪忠(1967-),男,江苏无锡人,硕士,副教授,研究方向为数据库技术、数据挖掘和网络安全。E-mail:qxzvb@163.com
通信地址:214122 江苏省无锡市江南大学物联网工程学院
Address:School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,Jiangsu,P.R.China

