异构超混沌广义同步系统构造及其电路仿真

张小红，周勇飞

(江西理工大学信息工程学院，江西 赣州 341000)

异构超混沌广义同步系统构造及其电路仿真

张小红，周勇飞

(江西理工大学信息工程学院，江西 赣州 341000)

在三维新混沌Chen系统基础上构建了一个四维超混沌系统。根据Lyapunov稳定性原理，采用自适应控制方法，在新构建的四维超混沌系统和四维超混沌Chen系统之间设计广义同步控制器，对控制器中的变量参数估计值和外部参数值进行广义同步实现的可行性进行讨论，进而将异构系统的广义同步问题转换为对控制器的选择。通过对不同参数估计值的比较分析得出合适的取值，达到了良好的广义同步效果。最后设计了一种实现广义混沌同步的基本电路原理图，数值仿真和电路实验结果表明了该方法的有效性，以及电路的可行性和实用性。

超混沌系统；参数对比；广义同步；电路仿真

1 引言

本文根据三维新混沌Chen系统[8]，在其基础上增加参数变量构建了一个新的四维超混沌系统，并验证了其超混沌特性，设计了相应的基本电路原理图。基于Lyapunov稳定性原理[9,10]，采用自适应控制方法[11,12]，构造了广义同步控制器，通过对变量参数的取值对比讨论，将新构建系统作为驱动系统，超混沌Chen系统作为响应系统，在Matlab软件平台上实现了广义同步。最后，设计了一种实现异构超混沌广义同步电路，电路结果证实了该系统的复杂动力学和同步特性，也表明了其在实际应用中的价值。

2 广义混沌同步系统构建

考虑如下两个耦合系统：

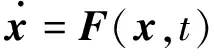
(1)

(2)

在本文中考虑参数估计值对比，将系统(1)和系统(2)进行拆分改写为如下形式：

(3)

(4)

其中f∈Rm，g∈Rn，Θ∈Rm为参数向量，Φ∈Rn为Θ的估计值，U∈Rn为广义同步控制器，则系统动力学误差为：

g(Y)+G(Y)Φ-Ψf(X)-ΨF(X)Θ+U

(5)

定理1 对于驱动系统(3)和响应系统(4)，当选取广义控制器为：

U=-g(Y)+Ψf(X)-

[G(Y)-ΨF(X)]Θ-δe

(6)

参数自适应率为：

(7)

其中δ为外部参数且是大于零的常数，那么系统(3)和(4)将达到广义同步。

□

3 超混沌系统的构建及动力学分析

Chen介绍的一种新三维混沌系统[8]，其动力学方程为：

(8)

本文旨在式(8)的基础上构造一个新的四维超混沌系统，考虑到新系统必须具备复杂非线性特性，在参数选配和变量反馈设计上进行了反复试验，新系统方程如下：

(9)

其中，a=5,b=-12,c=-3.5,d=0.7,e=0.5，通过计算机数值仿真得到如图1所示的轨迹相图。

对于一个动力学系统，判断其是否为超混沌系统一般可依据以下几个条件：

(1)是否具有耗散性结构；

(2)动力学系统方程模型中不稳定维数至少为二维，且其中非线性项的个数要不少于一个；

(3)该系统中Lyapunov指数值有至少两个大于零。

3.1 耗散性分析

Figure 1 Trajectory phase diagram of new construction four-demensional system图1 新构建四维系统的轨迹相图

3.2 平衡点稳定性分析

令方程(9)中各式为0可求得系统平衡点，解得系统唯一平衡点S0=(0,0,0,0)，然后对其线性化得到Jacobi矩阵为J：

代入S0，令det(J-λI)=0，特征方程为λ4+9.8λ3-42.85λ2+54.25λ+147=0，计算可得其特征值为λ1=λ2=λ3=1,λ4=0.96。根据Routh-hurwitz条件判定准则[13]，平衡点S0是系统不稳定的鞍点，因此系统在鞍点处是不稳定的。

3.3 Lyapunov指数性质

混沌吸引子中任意相空间轨迹线之间会表现为一种互斥的形式，任意两轨迹线之间的距离也会以指数速率相互分离，Lyapunov指数就是定量描述轨迹线彼此间的排斥和吸引的量，是混沌系统的重要特征。本文采用Jacobi方法计算系统(9)的Lyapunov指数值(简记为LE)，得LE1=6.1458，LE2=3.1151，LE3=-1.5185，LE4=-5.8928。图2为四维系统的Lyapunov指数图，系统吸引子的分形维数(记为DL)为：

表明这个新构建的四维系统LE维数是分数维。综上分析，该新构建四维系统为超混沌系统。

Figure 2 Lyapunov index phase diagram of four-demensional system图2 四维系统Lyapunov 指数相图

从上述对新构建的超混沌系统动力学分析可知，新系统具有超混沌的所有特性(两个大于0的Lyapunov指数)，代表动力系统轨道在相空间中分离特性的Lyapunov指数的快速分离。即使这样简洁的四维系统也能产生丰富的吸引子运动轨迹，实际上这也为今后从硬件方面实现提供了便捷的条件，彰显了其复杂非线性动力学优势。

4 异构超混沌系统同步仿真

超混沌Chen系统具有丰富的动力学特征，其数学模型可表示为：

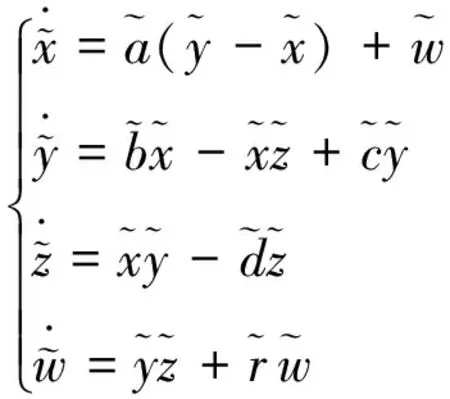
(10)

驱动系统方程：

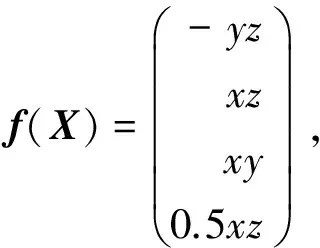
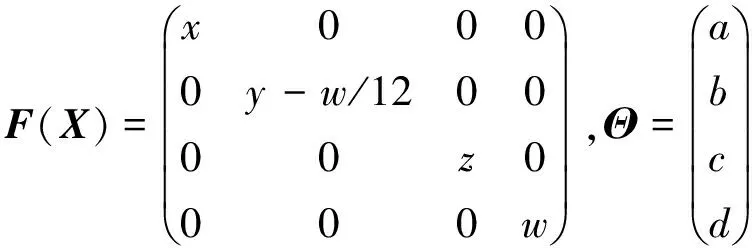
响应系统方程：

根据定理1，令广义控制器U=(U1,U2,U3,U4)T，则可表示为：

相应的参数自适应率为：

系统仿真中采用步长h=0.0001的四阶-龙格库塔方法，取矩阵Ψ为单位矩阵。本文中广义同步控制器是采用自适应控制方法进行设计构造，参数估计值Φ和外部参数δ的取值将决定广义同步控制器的选择，从而影响系统是否能够实现广义同步。通过计算机数值仿真分别取数估计值Φ为(5,-10,-3,0.4)、(5,-12,-3.5,0.7)，外部参数δ为30、50，得到如图3所示的仿真效果图。

Figure 3 System synchronous simulation results图3 系统同步仿真效果图

图3a和图3b为δ=50，Φ分别为(5,-10,-3,0.4)、(5,-12,-3.5,0.7)时的同步轨迹图，图3c和图3d为Φ取(5,-12,-3.5,0.7)，δ分别为30、50时的同步轨迹图。实验结果表明，取合适的参数估计值Φ和外部参数δ，系统达到同步的效果很明显，且δ的取值对同步效果影响更大。

5 超混沌系统广义同步电路实现

根据系统方程，设计包含实现驱动电路、响应电路和广义同步电路三部分组成的电路模块，如图4～图8所示。其中运算放大器为LM347，模拟乘法器为AD633，各电路元件的取值由系统方程参数决定。模拟乘法器实现系统中的非线性项，运算放大器实现电路中的加减。

为了取值方便，设τ=t/(10RC)，因此可以得到如下无量纲标准化方程，驱动系统电路表示为：

(11)

响应系统电路表示为：

Figure 4 Schematic diagram of generalized chaos synchronization circuit图4 广义混沌同步电路总图

Figure 5 Schematic diagram of drive system图5 驱动系统电路原理图

Figure 6 Schematic diagram of response system图6 响应系统电路原理图

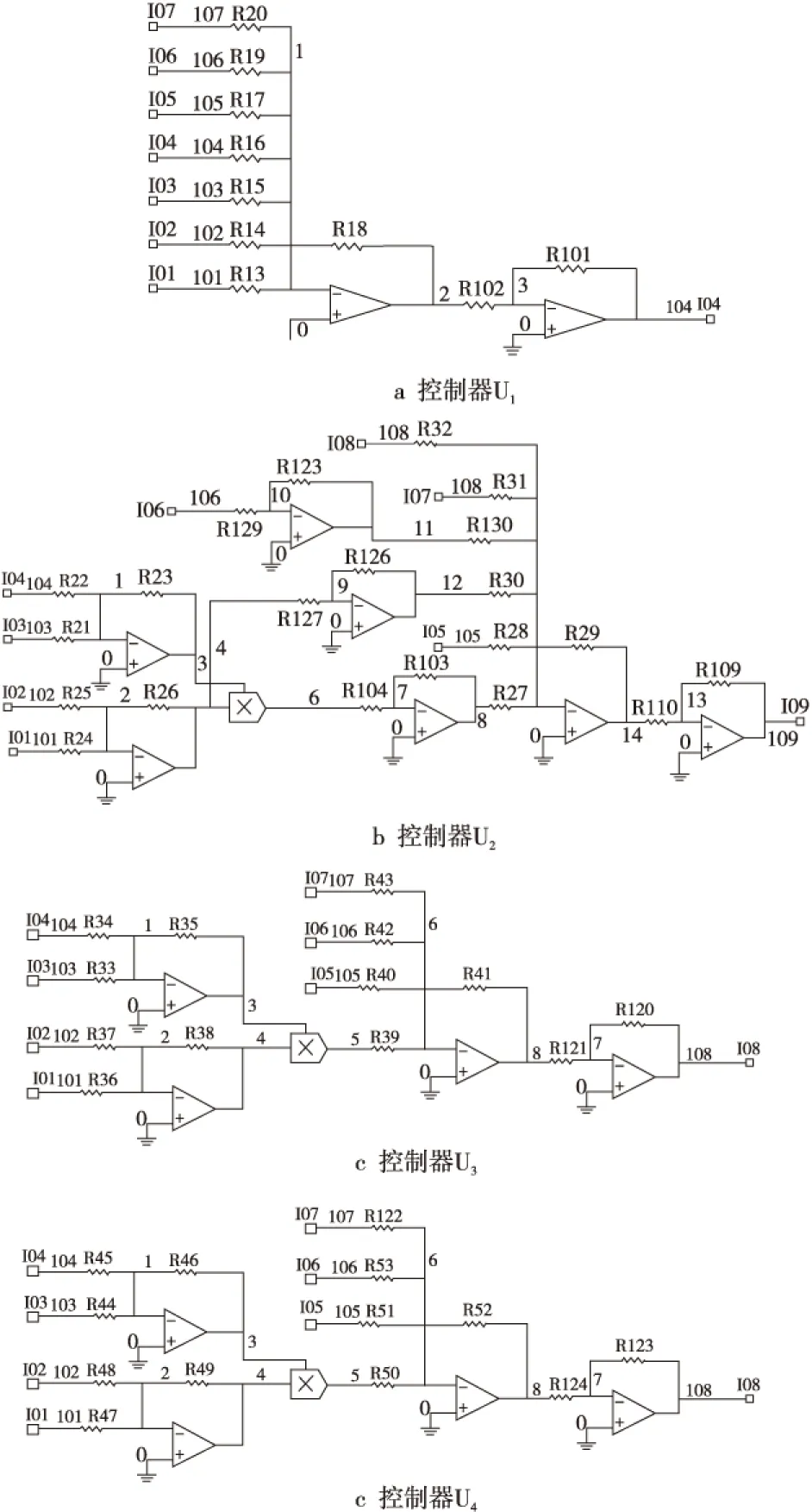
Figure 7 Circuit subgraph of generalized synchronized controller图7 广义同步控制器子图

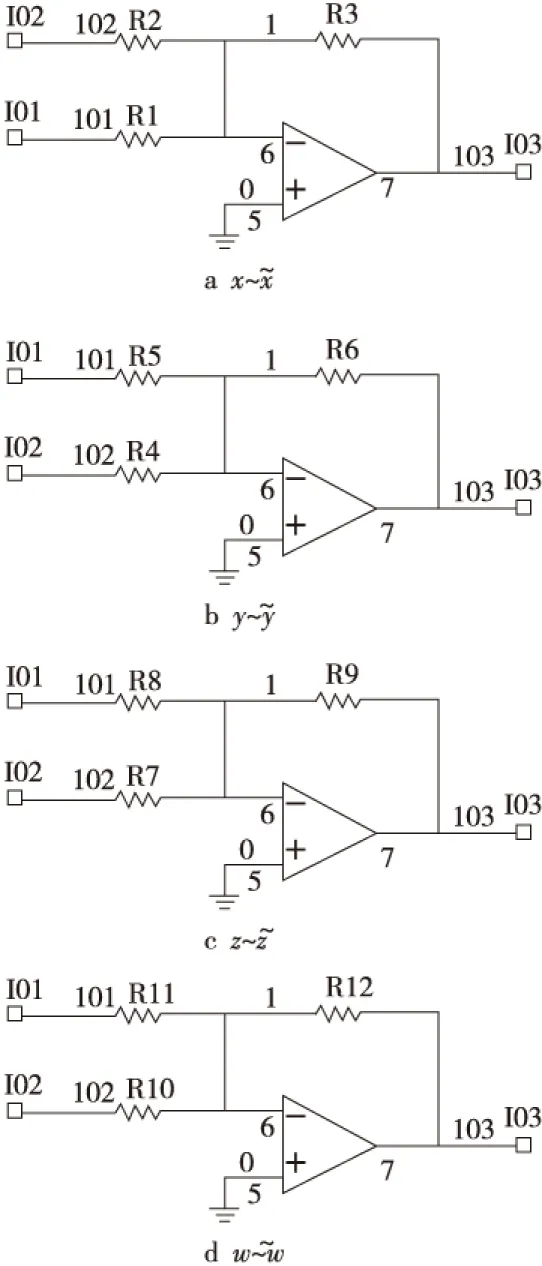
Figure 8 Circuit subgraph of system error图8 系统误差电路子图

(12)

在电路图中令Rx,Ry,Rz,Rw,Rx′,Ry′,Rz′,Rw′=10 kΩ，C1,C2,C3,C4,C5,C6,C7,C8=10 nf。将式(11)、式(12)分别和式(9)、式(10)对比可得：Rx1=20 kΩ，Rx2=100 kΩ，Ry1=8.33 kΩ，Ry2=100 kΩ，Ry3=100 kΩ，Rz1=28.57 kΩ，Rz2=100 kΩ，Rw1=142.86 kΩ，Rw2=100 kΩ，Rx′1=2.86 kΩ，Rx′2=2.86 kΩ，Rx′3=100 kΩ，Ry′1=14.29 kΩ，Ry′2=100 kΩ，Ry′3=8.33 kΩ，Rz′1=100 kΩ，Rz′2=33.33 kΩ，Rw′1=100 kΩ，Rw′2=200 kΩ。取参数估计值为(5,-12,-3.5,0.7)，δ=50时，对应于广义控制器中电阻的取值如下：R13=10 MΩ，R14=2 MΩ，R15=1 MΩ，R16=200 kΩ，R17=2 MΩ，R18=10 MΩ，R19=70 MΩ，R20=70 MΩ，R27=10 MΩ，R28=10 MΩ，R29=10 MΩ，R30=833.3 kΩ，R31=10 MΩ，R32=200 kΩ，R130=1.16 MΩ，R39=10 MΩ，R40=10 MΩ，R41=10 MΩ，R42=22.8 MΩ，R43=200 kΩ，R50=10 MΩ，R51=20 MΩ，R52=10 MΩ，R53=200 kΩ，R122=17 MΩ。为了方便，其他电阻取值统一为100 kΩ，实验结果如图9和图10所示。

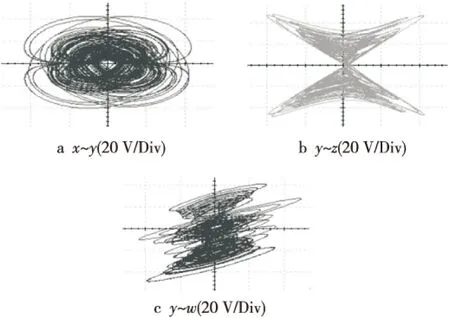
Figure 9 Trajectory diagram of drive system’s circuit图9 驱动系统电路轨迹图

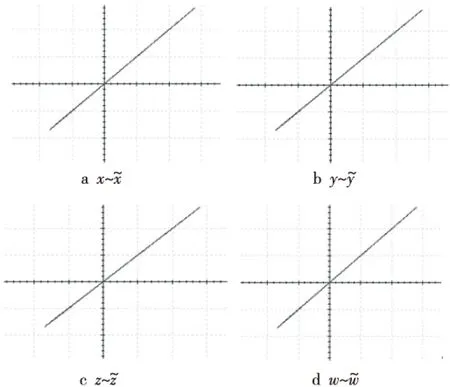
Figure 10 Trajectory diagram of generalized choas synchronization circuit图10 广义混沌同步电路轨迹图

6 结束语

本文构造出一个新的四维超混沌系统，并对其超混沌特性进行了理论和电路仿真分析。对于同步分析，关键一点在于控制器中外部参数δ的取值，通过取不同值对比讨论，得到了一个合适的控制器，从而使驱动系统和响应系统达到同步。最后，在Multisim电路仿真软件上设计了一种实现异结构超混沌广义同步电路，对于各部分电路模块将其各自封装为一个子电路，使得电路模块结构清晰，实验结果验证了其有效性和实用性。新构建的超混沌系统在保密通信、智能优化、图像辨识、模糊控制等方面具有潜在的应用价值，也为今后硬件集成实现提供一定可借鉴的参考价值。

[1] Pecora L M, Carroll T L. Synchronization in chaotic systems[J]. Physics Review Letters, 1990, 64(6):821-824.

[2] Wang Guang-yi, Zheng Yan, Liu Jing-biao. A hyperchaotic Lorenz attractor and its circuit implementation[J]. Acta Physica Sinica, 2007, 56(6):3308-3313.(in Chinese)

[3] Bowong S, Moukam Kakmeni F M. Synchronization of uncertain chaotic systems via back stepping approach[J].Chaos, Solitions and Frantals,2004,21:999-1011.

[4] Zhu Z W, Leung H. Adaptive identification of nonlinear systems with application to chaotic communications[J]. IEEE Transactions on Circuits and Systems-I, 2000, 47(7):1072-1080.

[5] Lu Chi-mei. A 4-D four-wing chaotic system and its circuit implementation[J]. Information and Electronic Engineering, 2011, 9(2):229-234.(in Chinese)

[6] Tang Liang-rui, Li Jing, Fan Bing. A new four-dimensional hyperchaotic system and its circuit simulation[J]. Acta Physica Sinica, 2009, 58(3):1446-1455.(in Chinese)

[7] Long Yan, Chen Di-yi, Yang Fu-zeng. New hyper-chaos and its adaptive synchronization control [J]. Electronic Design Engineering, 2010, 18(7):63-67.(in Chinese)

[8] Liu Wen-bo, Chen Guan-rong. A new chaotic system and its generation[J]. International Journal of Bifurcation and Chaos, 2003, 13(1):261-267.

[9] Li Chun-biao, Hu Wen. Synchronization methods and properties of the improved chaotic system with constant Lyapunov exponent spectrum[J]. Acta Physica Sinica, 2010, 59(2):801-815.(in Chinese)

[10] Liu Yan, Lv Ling. Synchronization of N different coupled chaotic systems with ring and chain connections[J]. Applied Mathematics and Mechanics (English Edition), 2008, 29(10):1299-1308.

[11] Zhang Ruo-xun, Yang Shi-ping. Modified adaptive controller for synchronization of incommensurate fractional-order chaotic systems[J]. Chinese Physics B, 2012, 21(3):030505.

[12] Aghababa M P. Design of an adaptive finite-time controller for synchronization of two identical/different non-autonomous chaotic flywheel governor systems[J]. Chinese Physics B, 2012, 21(3):030502.

[13] Chen Yong, Yan Zhen-ya. Chaos control in a new three-dimensional chaotic T system[J]. Communications in Theoretical Physics, 2008, 49(4):951-954.

附中文参考文献：

[2] 王光义, 郑艳, 刘敬彪. 一个超混沌Lorenz吸引子及其电路实现[J]. 物理学报, 2007, 56(6):3308-3313.

[5] 鲁池梅. 一个四维四翼混沌系统及其电路实现[J]. 信息与信息工程, 2011, 9(2):229-234.

[6] 唐良瑞, 李静, 樊冰. 一个新四维自治超混沌系统及其电路实现[J]. 物理学报, 2009, 58(3):1446-1455.

[7] 龙燕, 陈帝伊, 杨福增. 超混沌系统的电路仿真及其自适应同步[J]. 电子设计工程, 2010, 18(7):63-67.

[9] 李春彪, 胡文. 改进恒Lyapunov指数谱混沌系统的同步方法与特性研究[J]. 物理学报, 2010, 59(2):801-815.

ZHANG Xiao-hong,born in 1966,PhD,professor,her research interests include secure communication, and chaos synchronization.

周勇飞(1988-),男,江西临川人，硕士生，研究方向为混沌同步电路和非线性动力学。E-mail:yongfeitop@126.com

ZHOU Yong-fei,born in 1988,MS candidate,his research interests include chaos synchronization circuit, and nonlinear dynamics.

Generalized synchronization system construction of heterogeneous hyperchaotic and its circuit simulation

ZHANG Xiao-hong,ZHOU Yong-fei
(School of Information Engineering，Jiangxi University of Science and Technology，Ganzhou 341000,China)

A four-dimensional hyperchaotic system is built based on the three dimensional chaotic Chen system. According to the Lyapunov stability theory, using the adaptive control method, a generalized synchronization controller is designed between the newly constructed four-dimensional hyperchaotic system and the four-dimensional hyperchaotic Chen system. The feasibility of generalized synchronization for the variable parameters estimates and the external parameter values in the controller is discussed, and then the generalized synchronization of heterogeneous systems is converted to the choice of controller. Through comparative analysis of different parameter estimates, appropriate values in the controller can be obtained to achieve the generalized synchronization. Finally, a generalized synchronization circuit is designed. The results of numerical simulation and circuit experiment demonstrate the validity of the method as well as the effectiveness and usefulness of the circuit.

hyperchaos system;parameters comparison;generalized synchronization;circuit simulation

2012-09-20;

2012-11-30

国家自然科学基金资助项目(11062002)；江西省自然科学基金资助项目(2010GZS0083)；江西省教育厅科技项目(GJJ11470)

1007-130X(2014)03-0551-07

TP391.9

A

10.3969/j.issn.1007-130X.2014.03.031

张小红(1966-),女,河北昌黎人，博士，教授，研究方向为保密通信和混沌同步。E-mail:xiaohongzh@263.net

通信地址：341000 江西省赣州市江西理工大学信息工程学院

Address:School of Information Engineering，Jiangxi University of Science and Technology，Ganzhou 341000,Jiangxi,P.R.China