二元域上线性半群到任意域上线性半群的同态
朱 捷, 顾秋宇, 刘 莹, 杜广环, 王佳秋
(黑龙江科技大学 理学院,黑龙江 哈尔滨 150027)
0 引言
线性半群同态近年来引起许多学者关注,已成为矩阵代数中重要的研究课题[1-9].我们描绘了F2上的n阶线性群到域K上的m阶线性群(n=m=2,n=m≥3,n>m)的同态形式[1-3],从而完全描述了二元域F2上一般线性群的同态形式.但关于矩阵半群同态的描绘并不多[4-7],因此,我们使用矩阵计算与群的定义关系,结合文献[1-3]中已有的一般线性群结果,在文献[4]中通过引入标准型、延断型、平凡型、特殊型的概念,描述了M2(F2)到M2(K)的线性半群同态形式(其中同态是仅保持乘法,但未必保单位矩阵的映射).
本文结合文献中已有的关于一般线性群的结果,在正整数n≥m的限制下,给出了n>m,乘法半群同态(不必保幺元)为In,s,r或为φ1的延断(其中:若X为GL2(F2)的2阶元,φ1(X)=-1;若X=I2或X为3阶元,φ1(X)=1);当n=m时,乘法半群同态(不必保幺元)除In,s,r外,为标准型或线性非平凡解同态的延断.从而完全描述了Mn(F2)到Mm(K)的所有线性半群同态形式(仅保持乘法,未必保单位矩阵的映射).
1 基础知识
本文中,设K为域,n∈N+,SLn(K),GLn(K),Mn(K),DGLn(K)分别表示K上的n阶特殊线性群、一般线性群、线性半群、换位子群.以F2表示仅含两个元素的域,Tij(λ)(i≠j,λ∈K*,K*=K{0})为将n阶单位矩阵中(i,j)位置的元素易之以λ所得到的矩阵.对于X∈Mn(K),记iPX=P-1XP(其中P∈GLn(K)).
由[1-7]可知,下述映射φ是Mn(F2)到Mm(K)(n≥m)的半群同态(仅保持乘法,未必保单位矩阵).
Ⅰ标准型
1)φ(X)=PXτP-1,∀X∈Mn(F2),其中P∈GLm(K),τ:F2→K为嵌入.
2)φ(X)=P(X*τ)TP-1,∀X∈Mn(F2),其中P∈GLm(K),X*为X的伴随矩阵,τ同1).
Ⅱ延断型
设φ1:GLn(F2)→GLm(K)为非平凡同态,则称下列映射φ为φ1在Mn(F2)到Mm(K)的延断:
Ⅲ平凡型
设r,s∈{0,1,…,m},r≤s,P∈GLm(K),置
其中对于任意n,m∈N+,任意域K,称其为平凡同态,并以In,s,r表之.
Ⅳ特殊型
设ChK≠2,φ:M2(F2)→M2(K),
易证,φ为同态.
引理1[7]当n≥3时,有DGLn(F2)=SLn(F2)=GLn(F2).
引理2[4]设φ:M2(F2)→M2(K)为半群同态,则
1)φ=I2,2,2,I2,2,1,I2,2,0,I2,1,1,I2,1,0,I2,0,0.
2) 当ChK=2时,φ为标准型或标准型延断,或者为下述φ1的延断:
φ1(X)=PT12(1)P-1,
φ1(Y)=I2,
其中X∈GL2(F2)为任意2阶元,Y=I2或为3阶元,P∈GL2(K).
3) 当ChK≠2时,φ为下述φ1,φ2,φ3之一的延断:
φ1(X)=-I2,φ1(Y)=I2,
φ2(X)=P[1,-1]P-1,φ2(Y)=I2,
φ3(X)=P[-1,0]P-1,φ3(Y)=P[1,0]P-1,
其中X∈GL2(F2)为任意2阶元,Y∈GL2(F2)为任意3阶元.
4)φ为特殊型.
2 主要结论
定理1设φ:Mn(F2)→Mm(K)是半群同态,n>m,则仅当n=2,ChK≠2时,φ可以是φ1的延断,其它情形φ均为平凡型,其中

由InX=XIn=X,∀X∈Mn(F2),推出
iPφ(X)=X1⊕Om-s,X1∈Ms(K).
(1)
可推出φ1:X→X1是GLn(F2)到GLs(K)的群同态,由文献[3,定理2]知,当n≥3时,φ1是平凡的,即
∀X∈GLn(F2).
(2)
而当n=2时,若ChK≠2,由文献[3,定理1]知,除上述φ1为平凡外,还有下述形式:
φ1(X)=-1,φ1(Y)=1,
(3)
其中
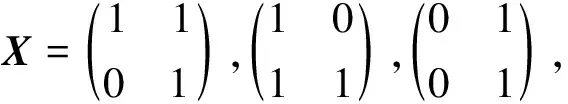
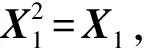
iPφ(In-1⊕0)=X1⊕Om-s.

iQφ(X)=Is⊕Om-s, ∀X∈GLn(F2),
iQφ(In-1⊕0)=Ir⊕Om-r.
从而对于任意X∈Mn(F2),rankX=n-1,有T1,T2∈GLn(F2),使X=T1(In-1⊕0)T2,可推出
iQφ(X)=Ir⊕Om-r.
于是,对于t∈{0,1,…,n-2},由
(4)
推出
iQφ(It⊕0)=Ir⊕O.
因此
iQφ(X)=Ir⊕Om-r,
∀X∈Mn(F2)GLn(K),
即φ为平凡型的.
对于(3)式,设φ(E11)=x∈K,由于T12(1)E11=E11,取象后,(-1)x=x,得x=0.不难指出
φ(X)=O, ∀X∈Mn(F2)GLn(K),
即φ是φ1的延断.证毕.
定理2设φ:Mn(F2)→Mn(K)为半群同态(只保持矩阵乘法),n≥3,则
1)φ为平凡的,即φ=In,s,r;
2)φ为标准型,或为标准型延断;
3)φ为下述φ3的延断,φ:GL3(F2)→GL3(K),其中ChK≠2,多项式2x2-x+1在K上分裂,且有P∈GL3(K),使
iPφ3(T12(1))=-I2⊕1,
iPφ3(T13(1))=1⊕(-I2),


证若存在sn,P∈GLn(K),使iPφ(In)=Is⊕On-s.则由定理2证明可知,∀X∈Mn(F2),有X1∈Ms(K),使iPφ(X)=X1⊕On-s.由文献[3,定理2]可知,iPφ(X)=Is⊕On-s,∀X∈GLn(F2).与定理2证明类似,可知φ=In,s,r.
如果φ(In)=In,则φ诱导出GLn(F2)→GLn(K)的群同态.置φ1=φ|GLn(F2),由引理1知,φ1是SLn(F2)到SLn(K)的群同态.如果φ1是平凡的,可知φ=In,s,r;如果φ1不是平凡的,由文献[2,定理1,3]有
Ⅰ) 当ChK=2时,φ1为标准型[2,定理3]);
Ⅱ) 当ChK≠2时,当且仅当n=3,多项式2x2-x+1在域K上分裂,存在P∈GL3(K),使iPφ1具有文献[2,定理1]中iPφ的形式.
如果上述Ⅰ)成立,则
iPφ1(X)=Xστ, ∀X∈SLn(F2)
(5)
或者
iPφ1(X)=((Xτ)-1)T, ∀X∈SLn(F2),
(6)
其中τ:F2→K为嵌入.
当(5)成立时,由于
(In-1⊕0)(A⊕1)=(A⊕1)(In-1⊕0),
∀A∈SLn-1(F2),
(In-1⊕0)Tnl(1)=In-1⊕0,l=1,2,…,n-1,
∀A∈SLn-1(F2).
(7)
令

上述式子取象后得
X(A⊕1)=(A⊕1)X,XTnl(1)=X.
推出
AX1=X1A, (A-In-1(1))X2=O,
X2ei=O,X3(A-In-1)=O,X4ei=O,
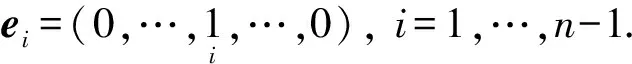
X1=aIn-1,X2=O(n-1)×1,X3=O1×(n-1).
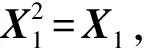
iPφ(In-1⊕0)=In-1⊕0
(8)
或
iPφ(In-1⊕0)=On.
(9)
若(8)发生,经(4)得,iPφ(It⊕On-t=On,不难指出
iPφ(X)=O, ∀X∈Mn(F2)GLn(F2),
即φ为标准型的延断.
若(7)发生,∀X∈Mn(F2),rankX=n-1,有T1,T2∈GLn(F2),使
X=T1(In-1⊕0)T2.
(10)
推出
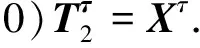
再由(4)不难指出,上式对于∀X∈Mn(F2)GLn(F2)成立,故φ为标准型.
若(6)成立,由GLn(F2)=SLn(F2),可知det (Xτ)=1,故(Xτ)-1=(Xτ)*.于是(6)为
iPφ1(X)=((Xτ)*)T, ∀X∈GLn(F2),
(11)
X((Aτ)-1)T⊕1)=(((Aτ)-1)T⊕1)X,XTln(1)=X,l=1,…,n-1,∀A∈GLn-1(F2),
其中

故又有
X1((Aτ)-1)T=((Aτ)-1)T⊕X1,
(((Aτ)-1)T-In-1)X2=O,
X3((Aτ)-1)T-In-1)=O,
X3ei=O,
可推出
经X2=X,得X=Enn或On.与上述讨论类似,由X=On,可推出φ为标准型φ1的延断.
当X=Enn时,则
iPφ(In-1⊕0)=((In-1⊕0)τ)*T.
经(10),(11)得,

=(((T1(In-1⊕0)T2)τ)*)T
=(Xτ)*T,
其中X∈GLn(F2),rankX=n-1.
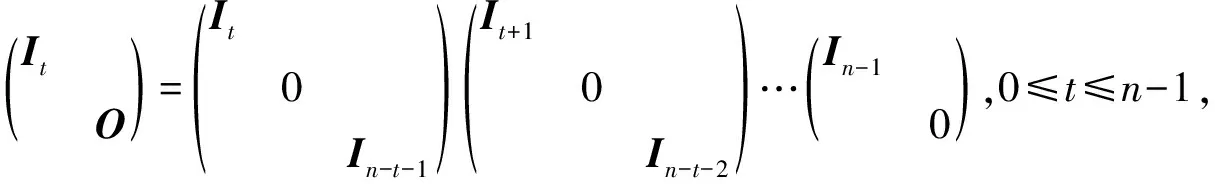
iPφ(It⊕0)=((It⊕0)τ)*T.
从而对于X∈Mn(F2),rankX=n-1,有S1,S2∈SLn(F2),使X=S1XS2.取象iPφ(X)=((Xτ)*)T,因此φ为标准型.
如果上述Ⅱ)成立,此时n=3,ChK≠2,φ1=φ3.
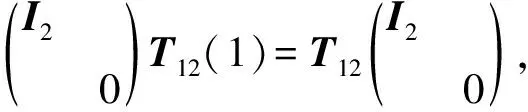
⊕x33.
又由T13(1)(I2⊕0)=I2⊕0,推出
⊕0.
再经(I2⊕0)T31(1)=I2⊕0,推出
故x11=x12=0,即iPφ(I2⊕0)=O.由此不难指出φ为φ3的延断.证毕.
定理3设K为域,且φ:Mn(F2)→Mm(K)为乘法半群同态(不必保幺元),n≥m,
1) 若n>m,则φ=In,s,r或为下述φ1的延断:
2) 若n=m,则除φ=In,s,r外,φ为标准型或为线性非平凡解同态的延断.
参考文献:
[1] 朱捷,张晓光,母丽华.F2上线性群GL2(F2)到域K上线性群GL2(K)的同态[J].黑龙江科技学院学报,2004,14(4):255.
[2] 朱捷.二元域上一般线性群到任意域上一般线性群的同态[J].吉林大学学报:理学版,2005,43(3):268.
[3] 朱捷,母丽华,王佳秋.F2上n阶线性群到域K上m阶线性群的同态[J].哈尔滨商业大学学报:自然科学版,2005,21(3):340.
[4] 朱捷,刘莹,杜广环.二元域上二阶线性半群到任意域上二阶线性半群的同态[J].黑龙江科技学院学报,2013,23(3):311.
[5] 朱用文,郭爱丽.带数乘的矩阵半群[J].数学学报:中文版,2010,53(6):1181.
[6] 左落粟,朱用文.矩阵单逆半群[J].吉林大学学报:理学版,2010,48(5):733.
[7] 朱用文,陈大亮.交换矩阵半群的可约性[J].数学学报:中文版,2010,53(5):905.
[8] 朱用文.正则矩阵半群[J].数学进展,2009,38(1):75.
[9] 华罗庚,万哲先.典型群[M].上海:上海科学技术出版社,1963.
——如何培养学生的创新思维

