p-adic典型群上轨道积分的若干性质
俞小祥
(江苏师范大学 数学与统计学院,江苏 徐州 221116)
0 Introduction
The study of intertwining operators plays an important role in Langlands program and harmonic analysis,it is raised from the study of Eisenstein series[1-3]and Eisenstein integrals[4-5].Recent breakthrough to study those operators attached to non-generic supercuspidal representations is to study the orbit integrals associated to them[6-8],since these integrals don't require to bear a Whittaker model,by doing so,one may relate the harmonic analysis on non-generic representations to generic ones.As the theories on generic representations[2,7]are fairly well known,this will find a way to approach the local Langlands program.
To save context,we'll freely use notations from[6-8],particularly from those in[9-11].However,we are not trying to expose the whole frame work mentioned above,but rather,only demonstrate some elementary and interesting properties of these orbit integrals.
Suppose Fis a p-adic field,let Glbe a quasi-split connected reductive classical group of rank l defined over F.Let M=GLn(F)×Gmbe the Levi subgroup of a maximal parabolic subgroup Pof Gl,where Gmis a subgroup of the same type of Gl,with rank m(l=n+m).Letτ′andτbe unitary irreducible supercuspidal representations of GLn(F)and Gm,respectively,withτ′ being ramified.Then the value of,A(s,τ′⊗τ,w0)h(e)〉at s=0is proportional to[10]
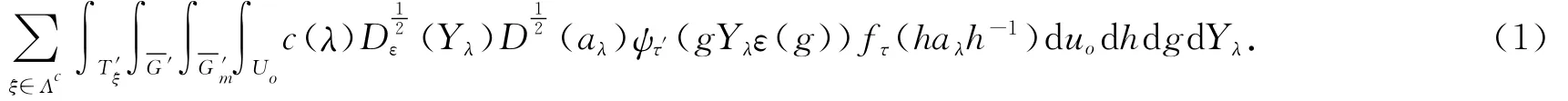
Here his a function which lies in the induction space IndGlP(τ′⊗τ⊗|det|s⊗1);ψτ′and fτare matrix coeffi-cients ofτ′andτ,respectively;Λcis the set of compact parameters;Uois the quotient of the twisted cen-;( )1( )tralizer of the orbit parametrized byλmodula that of the centralizerYdgand D2adhprovide inλλvariant measures on theε-conjugacy class of Yλand conjugacy class of aλ,respectively;and finally,Yλis related to aλunder norm correspondence.
1 Orbit integrals
Lemma 1Suppose G′is a reductive linear algebraic group defined over F,Γis a closed unimodular subgroup of G′,Kis a compact open subgroup of G′.If f∈Cc(G′/Γ)such that
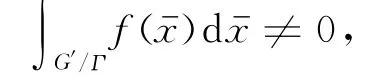
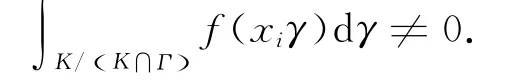
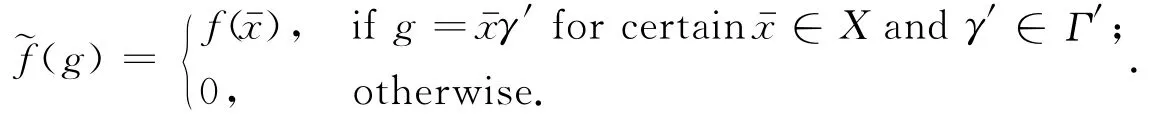
Then it's not hard to see that∈Cc(G′)and(gγ)=(g)=f)for any g∈G′,γ∈Γ′,wheregis the representative of gin G′/Γ.Normalize the measure onΓ′so that meas(Γ′)=1.Then

Here,dgis a left invariant measure on G′,the last equation is obtained by applying Lemma 1.2.5in[5].
Since Kis open compact and~fis compactly supported,
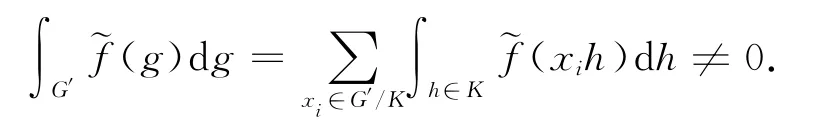
Therefore,there is at least one xisuch that
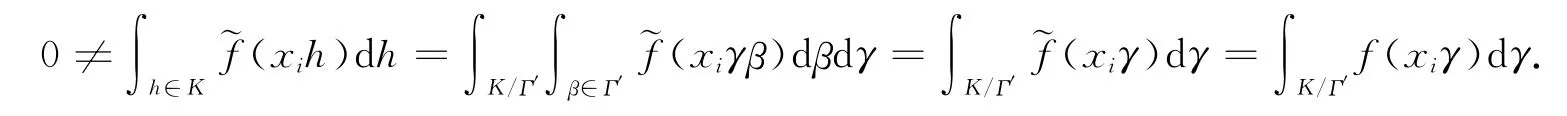
Let V′be the representation space ofτ′.Supposeψτ′(g)is defined by
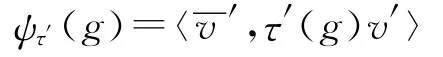
Theorem 1Let A(0,τ′⊗τ)be the expression in(1),then there is a functionalφon Cc(GLn(F)),so that
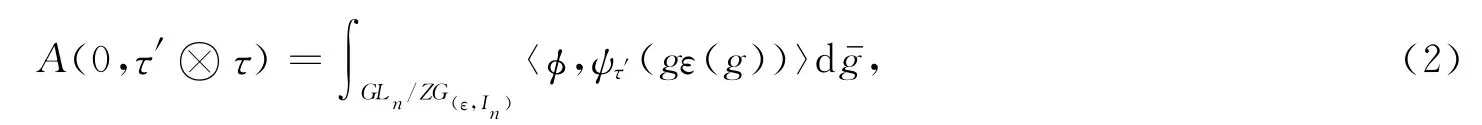
where Zis the center of GLn(F),G(ε,In)is the twisted centralizer of Inin GLn(F),dis a left invariant measure on GLn/ZGε,In.

We'll also define a right representationσof GLn(F)on Cc(GLn(F))by

Define a functional Pon Cc(GLn(F)/Z)by
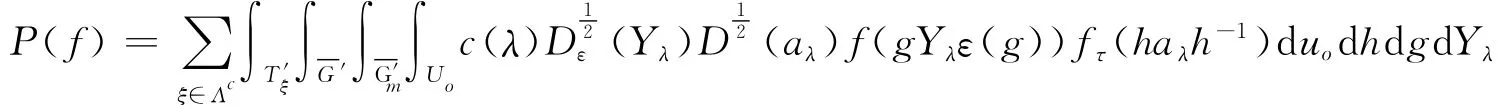
for any f∈Cc(GLn(F)).Then by the definition of P,it's directly checked that Pis linear on Cc(GLn(F))and
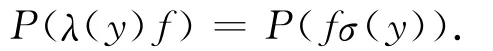
Applying Corollary 1.8.3in[5]toψτ′,there is one functionalφon Cc(GLn(F)/Z)so that(2)holds.
Let Kbe an open compact subgroup of GLn(F).Let ZK=K∩Z,G(ε,K)=G(ε,In)∩K.Then
Proposition 1(1)is nonzero only if for a matrix coefficientφ(x)of V′,

LetΓ=ZG(ε,In),thenΓis obviously closed and unimodular.One may regardψτ′(ge(g))as a function of GLn(F)/Γ,defined by
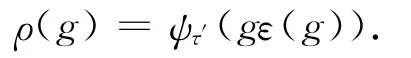
Then by Theorem 1and Lemma 1,(1)is nonzero only if

But

Then(4)can be rewritten as(3).
[1]Shahidi F.On the ramanujan conjecture and finiteness of poles for certain L-functions[J].Ann Math,1988,127(2):547.
[2]Shahidi F.A proof of Langlands conjecture on Plancherel measures:complementary series for p-adic groups[J].Ann Math,1990,132(2):1.
[3]Silberger A J.Introduction to harmonic analysis on reductive p-adic groups[M].Princeton:Princeton Univ Press,1979.
[4]Harish-Chandra.Harmonic analysis on reductive p-adic groups[M].Berlin:Springer-Verlag,1970.
[5]Harish-Chandra.Introducyion to harmonic analysis on reductive p-adic groups[M].Princeton:Princeton Univ Press,1979.
[6]Goldberg D,Shahidi F.On the tempered spectrum of quasi-split classical groups[J].Duke Math J,1998,92(2):255.
[7]Shahidi F.Twisted endoscopy and reducibility of induced representation for p-adic groups[J].Duke Math J,1992,66(1):1.
[8]Shahidi F.The notion of norm and the representation theory of orthogonal groups[J].Invent Math,1995,119(1):1.
[9]Yu Xiaoxiang.Prehomogenuity on quasi-split classical groups and poles of intertwining operators[J].Canad J Math,2009,61(5):691.
[10]Yu Xiaoxiang,Wang Dengyin.Norm correspondence on p-adic classical groups[J].J Algebra,2013,378:22.
[11]Yu Xiaoxiang.Residues of standard intertwining operators on p-adic classical groups.preprint.

