基于广义区间梯形模糊集的大学生素质评价模型

陈秀明, 胡贤德, 龚 芳, 程家兴,2

(1.安徽新华学院 信息工程学院,安徽 合肥 230088; 2.安徽大学 计算智能与信号处理教育部重点实验室,安徽 合肥 230039)

0 引言

大学生素质教育评价是对大学生素质教育的一种反馈调节系统,评价指标体系的构建依据是高校素质教育目标.做好大学生素质教育评价的组织实施是实现高校素质教育目标的重要环节[1]．然而，目前的教育评价模型在很大程度上束缚了大学生素质教育的发展[2]．这些模型的缺陷具体表现在:过度重视学习成绩，轻视综合素质培养;注重共性引导，忽视个性发展;注重教师主导作用，轻视学生主体作用;轻视大学生的人文素质、心理素质、社会交往能力;评价模型与社会需求存在严重错位．因此需要构建更加科学合理的素质教育评价模型[3]．文献[4]采用层次分析法、模糊集等方法建立了大学生体育素质教育的评价模型．文献[5]利用BP神经网络建立了大学生安全教育评价模型．文献[6] 应用模糊数学评价法构建了大学生廉洁教育评价指标体系，提出了大学生廉洁教育模糊综合评价模型．文献[7]采用灰色关联分析与模糊层次组合提出一种评价大学生素质教育模式的方法．文献[8]运用信息融合理论、Agent技术等研究评价过程中的多源数据融合、评价指标和个性化综合评价模型等问题．文献[9]对大学生综合素质进行实证分析，对42个指标进行主成分分析，验证指标体系构建的合理性，构建大学生素质评价模型．

实际上,不同的评价者对大学生素质的权重分配存在着差异,并且权重分配信息通常是采用模糊语言表达的．可见,实际的大学生素质评价问题具有模糊性、区间性、多属性等特点,以往文献中的方法不适合处理模糊语言信息的大学生素质评价模型问题．为此本文设计一种新的模型来处理大学生素质评价问题．

1 广义区间梯形模糊数的概念与运算

1.1 广义梯形模糊数的定义与重心

(1)

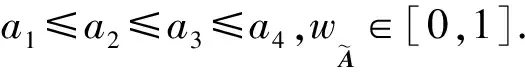
解得

(2)

(3)

图1 模糊数集合

表1 本文方法与文献[13]方法结果对比

1.2 广义区间梯形模糊数的定义及运算

图2 广义区间梯形模糊数

(4)

(5)

(6)

(7)

(8)

2 模糊语言与广义梯形模糊数的转化

根据文献[10],模糊语言可转化为广义区间梯形模糊数,见表2.

表2 模糊语言与广义区间梯形模糊数的转换关系

3 素质教育评价问题描述与模型表示

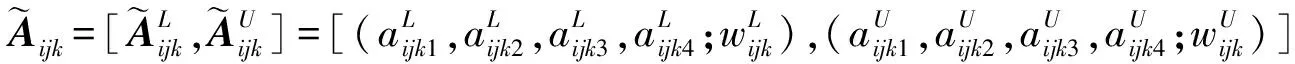
(9)

(10)

引入广义区间梯形模糊集的混合集成算子ITHA来计算综合评价值,即

4 算例分析

表3 素质指标的重要性

假设有4名大学生A1，A2，A3，A4需要进行素质评价,选取身心素质(C1)、道德品质(C2)、专业素养(C3)和实践素质(C4)作为4个评价指标,DM1,DM2,DM3分别代表学生自我评价、管理部门评价者和社会评价者．其中,素质指标的重要性见表3,3位评价者的评分信息见表4．

表4 3位评价者的评分信息

评价步骤如下:

1) 将模糊语言信息转化为区间梯形模糊数．

2) 采用广义区间梯形模糊集的有权算术集成算子,将3位评价专家的个人评价综合成综合评价信息．

3) 利用广义区间梯形模糊集的混合集成算子来计算综合评价值,此步骤中可根据具体问题赋予不同的权值．本例中,采用平均权重方法，即w=(0.25,0.25,0.25,0.25),得到综合评价值．

4) 根据公式(2),(7),计算得到各个模糊数的重心和距离，如表5所示.

表5 重心和距离计算结果

由以上结果可知,A1≻A2≻A3≻A4,即第1位学生的综合素质优于其他3位学生．

5 结论

广义区间梯形模糊集可以准确地描述各种属性值和权值均为模糊语言表达的群体决策问题．本文提出的评价方法是基于广义区间梯形模糊集的有权算术集成算子和混合集成算子给出的,同时给出了具体的评价步骤．算例结果显示该模型处理大学生素质评价问题是有效的．

参考文献:

[1] 朱中华.关于构建高校素质教育评价体系的思考[J].教育探索,2006(3):61.

[2] 丛玉燕.素质教育呼唤科学的教育评价体系[J].山西经济管理干部学院学报,2009,17(3):103.

[3] 郑媖.高校学生能力素质模型构建及其应用研究[D].武汉:武汉大学,2013.

[4] 吴晓强.我国普通高校体育素质教育评价模型的研究[J].安徽体育科技,2003(2):68.

[5] 王新泉.基于人工神经网络的大学生安全教育评价模型的研究[J].河南教育学院学报:哲学社会科学版,2006,25(5):111.

[6] 龙仕平，童洪志.大学生廉洁教育评价指标体系与模糊评价模型的建构[J].学校党建与思想教育,2013(3):89.

[7] 刘君，罗晓媛.素质教育在关联分析下的模糊层次综合评价模型[J].黑龙江科技信息,2012(14):202.

[8] 方宝红.基于多源信息融合的本科生综合素质评价研究[D].上海：东华大学,2011.

[9] 唐仁春.我国普通高校本科生综合素质多重视角评价研究[D].长沙:中南大学,2009.

[10] Liu P.A weighted aggregation operators multi-attribute group decision-making method based on interval-valued trapezoidal fuzzy numbers[J].Expert Systems with Applications,2011,38(1):1053.

[11] Chen S H.Ranking fuzzy numbers with maximizing set and minimizing set[J].Fuzzy Sets and Systems,1985,17(2):113.

[12] Chen S J,Chen S M.A new method for handling multicriteria fuzzy decision-making problems using FN-IOWA operators[J].Cybernetics & Systems,2003,34(2):109.

[13] Cheng C H.A new approach for ranking fuzzy numbers by distance method[J].Fuzzy Sets and Systems,1998,95(3):307.

[14] Wei S H,Chen S M.Fuzzy risk analysis based on interval-valued fuzzy numbers[J].Expert Systems with Applications, 2009,36(2):2285.

[15] Chen S M,Chen J H.Fuzzy risk analysis based on ranking generalized fuzzy numbers with different heights and different spreads[J].Expert Systems with Applications,2009,36(3):6833.