融合邻域信息的k-近邻分类
林耀进,李进金,,陈锦坤,马周明
(1.闽南师范大学 计算机科学与工程系,福建 漳州 363000; 2. 闽南师范大学 数学与统计学院,福建 漳州 363000)
k-近邻法是一种非常简单有效的分类算法,广泛应用于数据挖掘和模式识别的各个领域[1-3]。其基本思想是通过计算寻找训练集中距离待分类样本最近的k个邻居,然后基于它们的类别信息,依据投票的原则对待分类样本的类别进行判定。k-近邻算法的分类精度很大程度受影响于样本之间距离的度量。
近几年,出现了许多改进的距离度量方法以提高k-近邻算法的分类性能,主要分为局部距离和全局距离两大类。在传统的全局距离度量方面,针对异构特征,提出了相应的距离度量方法,如:值差度量(value difference metric, VDM)、修正的值差度量(modified value difference metric, MVDM) 和异构欧几里德—重叠度量(heterogeneous euclidean-overlap metric, HEOM)等[4-5]。另外,许多学者考虑了样本之间的权重以增强样本之间的相似性。Hu等[6]提出一种通过梯度下降的方法估计样本之间的权重进行改进KNN的分类算法;Wang等[7]提出一种简单的自适应距离度量来估算样本的权重。同时,一些学者通过属性加权或属性选择途径改进距离度量[8-9]。在局部距离度量方面,许多方法利用局部自适应距离处理全局优化问题,如:ADAMENN中的自适应距离,WAKNN中的权重校正度量方法及DANN中的差异化自适应度量方法[10-11]。
上述方法虽能有效地度量样本之间的距离,但基本上都是从单一的距离进行考虑,存在着以下缺点:1)并未考虑样本之间的邻域结构;2)易受噪声的影响;3)不能处理多模态分布问题。因此,本文受推荐中的用户群体影响概念的启发[12],提出了一种融合样本邻域信息的k-近邻分类算法。
1 k-近邻分类法
k-近邻分类法是一种非常简单有效的用于分类学习和函数逼近的算法。给定由n个样本标签对组成的数据集D,D={(x1,c1),(x2,c2),…,(xn,cn)},其分类的任务在于获取映射函数f,使得能正确预测无标签样本。设Nk(x)为测试样本x的k-近邻集合,k-近邻分类法在于通过测试样本x的k-近邻进行大众数投票进行确定x的标签,其公式为
(1)
式中:cj为样本xj的类标签,I(·)为指示函数,当ci与cj一样时,I(cj=ci)=1,否则,I(cj=ci)=0。
2 融合邻域信息的k-近邻分类算法
2.1 邻域信息的影响
传统的k-近邻分类算法本质上是利用样本个体与个体之间的距离(寻找对测试样本影响最大的前k个近似邻居)来预测测试样本的类标签,该预测只是简单地考虑样本个体之间的相似性,而忽略了样本的邻域信息。因此,在计算样本个体距离时不仅要考虑样本个体之间的距离,也要考虑样本邻域信息产生的距离。图1清楚地描述了样本邻域信息产生的影响作用,从图1可以看出,虽然样本x1与x2之间的距离与样本x1与x3之间的距离相等,即d(x1,x2)=d(x1,x3),但是样本x1的邻域信息与x3的邻域信息之间包含更多的大量的共同邻居,则从认识论的角度出发,d(x1,x3)≥d(x1,x2)。根据以上分析,可以得出准则1。
准则1 考虑样本邻域信息的影响能更加精确地刻画样本之间的距离。
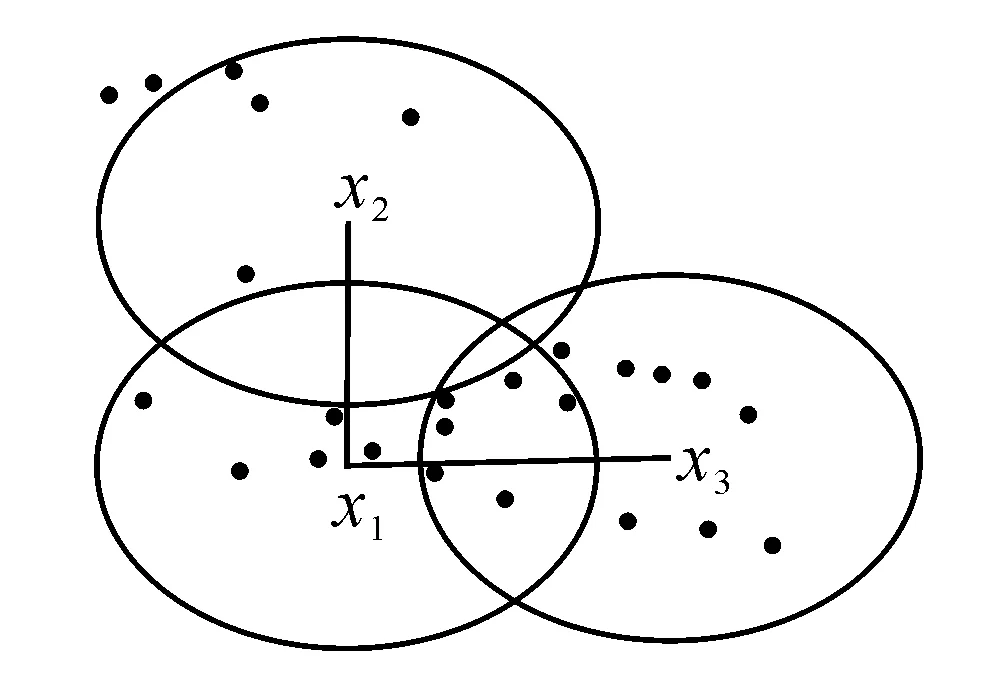
图1 样本邻域图Fig.1 Neighborhood of sample
2.2 样本邻域的定义
据2.1节分析可知,考虑样本邻域之间的距离可以更加精确地刻画样本之间的距离Δ,因此,寻找样本邻域对提高k-近邻分类算法具有重要的影响。本节中给出样本的度量空间及样本邻域的定义。
定义1[13]给定一个m维的样本空间Ω,Δ:Xm×Xm→X,称Δ是Xm上的一个度量,如果Δ满足:1)Δ(x1,x2)≥0,Δ(x1,x2)=0,当且仅当x1=x2,∀x1,x2∈Xm;2)Δ(x1,x2)=Δ(x2,x1),∀x1,x2∈Xm;3)Δ(x1,x3)≤Δ(x1,x2)+Δ(x2,x3),∀x1,x2,x3∈Xm;称〈Ω,Δ〉为度量空间。
在N维欧氏空间中,给定任意2点xi=(xi1,xi2,…,xiN)和xj=(xj1,xj2,…,xjN),其距离为
(2)
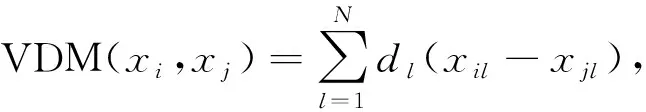
定义2 给定样本空间上的非空有限集合X={x1,x2,…,xm},对于X上的任意样本xi,定义其δ邻域为δ(xi)={x|x∈X,Δ(x,xi)≤δ},其中,0≤δ≤1。δ(xi)称为样本xi相应的δ邻域。
定义3 给定样本空间上的非空有限集合X={x1,x2,…,xm},对于X上的任意样本xi及xj,根据VDM公式,定义样本xi及xj之间的邻域距离为
(3)
性质1[13]给定一个度量空间〈Ω,Δ〉,一个非空有限样本集合X={x1,x2,…,xm}。如果δ1≤δ2,则有
1) ∀xi∈X:δ1(xi)≥δ2(xi);
根据定义3及性质1,随着样本距离δ的增大,样本邻域中所包含的对象数量随着增加,样本之间的区分度将降低。如图2所示,随着距离的增大,原来不属于同一邻域的样本x1、x2、x3变成处于同一邻域:即样本x1、x2、x3在图1中不属于同一邻域,而在图2中则处于同一邻域。根据以上分析,可以得出准则2。
准则2 选择样本邻域的大小影响着样本之间距离的精确刻画。
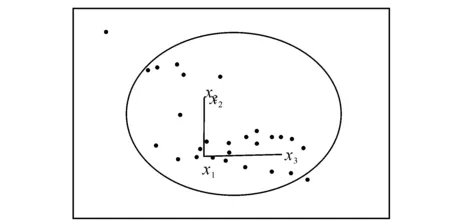
图2 δ减小后的样本邻域图Fig.2 Neighborhood of sample with smallerδ
3 算法设计
在对样本邻域影响分析的基础上,利用欧式距离计算样本之间的距离,用改进的VDM计算样本邻域之间的距离,设计融合样本邻域信息的k-近邻分类算法如下:
算法1 融合样本邻域信息的k-近邻分类算法(FK3N)。
输入:数据集D,测试样本x,距离阈值δ,近邻个数k;
输出:测试样本x的标签c(x)。
1)初始化c(x)=φ;
2)根据式(2)获取测试样本与训练样本的k/2个近邻R1;
3)根据式(3)获取测试样本邻域与训练样本邻域的k/2个近邻R2;
4)获得测试样本x的融合近邻集合R=R1∪R2后,即测试样本x的k近邻Nk(x);
5)根据式(1)获得测试样本x的类标签c(x)。
4 实验结果及分析
为了验证所提出算法的有效性,从UCI 数据集中挑选了6组数据。其中,为了验证算法的适用性,其数据集的类别从2类到3类,特征数从5~60,具体描述信息见表1。同时,进行2组实验,第1组实验与经典的分类算法KNN、NEC[13]、CART、LSVM进行比较;另一组检测在噪声数据影响下,本文所提出的FK3N与其他分类器的比较。
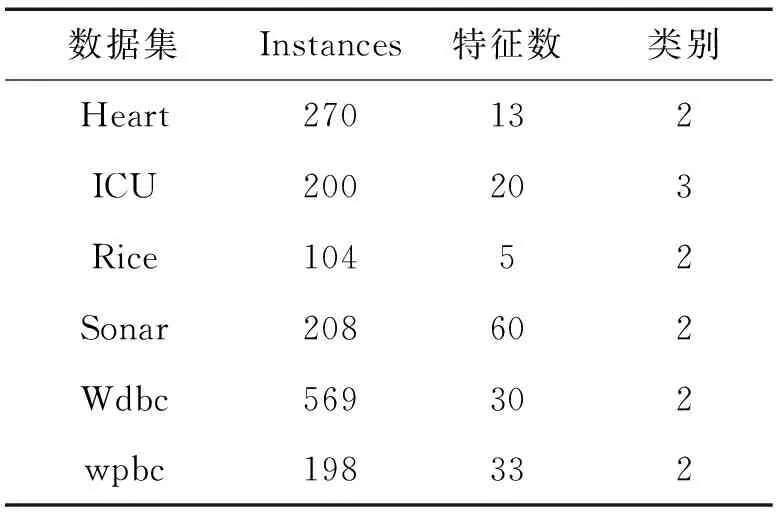
表1 数据描述
实验1 为了验证FK3N的分类性能,在本实验中,与其他流行的分类算法进行了比较,如表2。
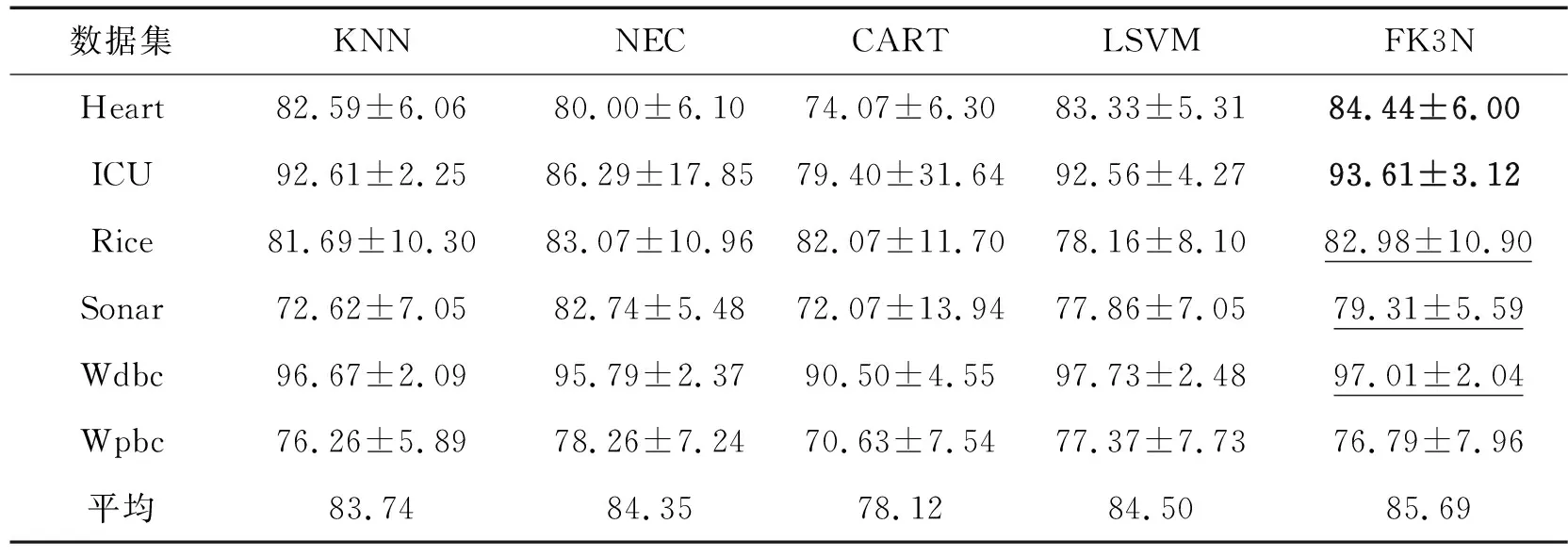
表2 不同分类器的分类精度比较
其中将FK3N、KNN涉及到的参数k设置为10,将FK3N、NEL涉及到的参数delta设置为0.1。为了显示标注FK3N在6个UCI数据集上的分类精度,在FK3N中加粗的代表分类精度最高,下划线代表分类精度第2。另外,在表2最后一行显示不同分类器的平均分类精度。从表2可以看出,FK3N虽然只在2个数据集上取得最优的分类效果,但是在其他3个数据集上取得第2(或并列)的分类精度。另外,在平均分类精度可以看出,FK3N取得最高的平均分类精度,比LSVM还高出1.19%。因此,从本实验可以看出,与其他流行的分类器相比,说明了本文提出的FK3N算法具有较为优越的分类性能。
实验2 为了考察FK3N的稳定性,在训练数据的属性中注入噪声。首先生成一个服从标准正态分布的m×n(m为样本数,n为属性数)的噪声数据,然后乘以系数a后加入原始训练数据中。本文设a的值为0.1。从表3可以看出,与其他分类器相比,在存在噪声情况下,FK3N在多个数据集上的分类精度取得良好的结果。

表3 噪声数据下不同分类器的分类精度比较
5 结束语
本文提出了一种FK3N分类算法。首先,从度量空间角度定义了样本邻域信息,分析了样本的邻域对能否精确地计算样本之间的距离具有重要的影响,提出了2条符合实际情况的准则;然后在计算样本个体之间的距离时,综合考虑了样本邻域之间的相似性;最后提出了一种获取最近邻的计算方法。在多个公开UCI数据集上的实验结果表明,本文方法在原始数据和噪声数据上分类性能优于或相当于其他相关分类器。
参考文献:
[1]COVER T, HART P. Nearest neighbor pattern classification[J]. IEEE Transactions on Information Theory, 1967 (13) : 21-27.
[2]WU X D, KUMAR V, QUINLAN J R, et al. Top 10 algorithms in data mining[J]. Knowledge and Information Systems, 2008,14(1) : 1-37.
[3]吕锋, 杜妮, 文成林. 一种模糊-证据kNN分类方法[J]. 电子学报, 2012, 40(12) : 2930-2935.
[4]WANG H. Nearest neighbors by neighborhood counting[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005,28 (6): 942-953.
[5]WILSON D R, MARTINEZ T R. Improve heterogeneous distance functions[J]. Journal of Artificial Intelligence Research, 1997 (6): 1-34.
[6]HU Q H, ZHU P F, YANG Y B, et al. Large-margin nearest neighbor classifiers via sample weight learning[J]. Neurocomputing, 2011, 74 (4): 656-660.
[7]WANG J, NESKOVIC , COOPER L.N. Improving nearest neighbor rule with a simple adaptive distance measure[J]. Pattern Recognition Letters, 2007, 28 : 207-213.
[8]KOHAVI R, LANGLEY P, YUNG Y. The utility of feature weighting in nearest neighbor algorithms[C]//Proceedings of the Ninth European Conference on Machine Learning. [S.l.], 1997.
[9]SUN Y J. Iterative RELIEF for feature weighting: algorithms, theories, and applications[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(6): 1035-1051
[10]MU Y, DING W, TAO D C. Local discriminative distance metrics ensemble learning[J]. Pattern Recognition, 2013, 46 (8): 2337-2349.
[11]SONG Y, HUANG J, ZHOU D, et al. IKNN: informative k-nearest neighbor pattern classification[C]//PKDD 2007. [S.l.], 2007: 248-264.
[12]林耀进, 胡学钢, 李慧宗. 基于用户群体影响的协同过滤推荐算法 [J], 情报学报, 2013, 32(3): 299-350.
[13]HU Q H, YU D R, XIE Z X. Neighborhood classifiers[J]. Expert Systems with Applications, 2008, 34 (2): 866-876.

