基于决策粗糙集的图像分割
李峰,苗夺谦,刘财辉,杨伟
(1.同济大学 计算机科学与技术系,上海 201804; 2.同济大学 嵌入式系统与服务计算教育部重点实验室,上海 201804)
图像分割是将图像细分为构成它的子区域或对象,把其中感兴趣的对象提取出来的技术和过程。它既是图像处理中的重要内容,又是由图像处理到图像分析的关键步骤。图像分割在实际中已得到广泛的应用,如工业自动化、文档图像处理、生物医学图像分析等方面。
Sezgin等[1]总结了2003年以前的40种经典的阈值分割方法,这些方法按照分割时考虑的图像信息分为6类:直方图形状、测试空间聚集度、熵、目标属性、空间相关性和局部灰度图。Sankar等[2]将粒计算和粗糙集思想运用于阈值分割,提出了一种基于粒计算和粗糙熵的目标提取方法。该方法主要解决灰度图像中物体之间的边界灰度值常常模糊的问题,图像信息具有较强的空间复杂性、相关性,处理过程中会遇到不完整和不确定性问题。Sankar等[3]还做了进一步的工作,将这种处理方式运用于运动目标检测。Sankar的方法是单阈值的分割,只是把图像分割成背景和感兴趣的目标区域,但有时感兴趣的目标是多个,所以为了能分割出多目标区域,Dariusz等[4]提出了自适应多阈值粗糙熵优化算法,这样可以比较灵活地处理一些特殊需求。这2种方法都是在灰度图像上进行处理,只是一维的,Dariusz等[5]又把处理的维度提升到两维。Dariusz等[6-7]针对粗糙集与图像分割的结合,还做了其他一系列工作。
上述的方法虽然解决了图像分割中模糊性的问题,但忽略了噪声对处理结果的影响。因为其使用的是Pawlak粗糙集模型,而Pawlak粗糙集模型使用的是绝对集合包含关系,对像素点的灰度值要求较严格,不能很好地处理带噪声的数据,所以上述方法都不宜处理带有噪声的图像。而决策粗糙集鲁棒性较好,能处理带噪声的数据,于是为了能够较好地处理带有噪声的图像,本文在文献[2]的基础上,结合决策粗糙集,提出一种能较好处理带噪声图像的基于决策粗糙集的图像分割方法。这里之所以选择单阈值分割这种简单情况,是因为方便阐述这种解决带噪声图像的思想,对于多阈值分割情况,可以在单阈值分割基础上进行扩展。
1 基础知识
目前图像分割的方法主要可以分为以下3类:基于阈值的图像分割、基于边缘检测和连接的图像分割以及基于区域的图像分割。其中基于阈值的图像分割是一种简单有效的图像分割方法,它用一个或几个阈值T将图像的灰度级分为几个部分,认为属于同一个部分的像素是同一个物体。如对于单阈值的图像分割,可以有
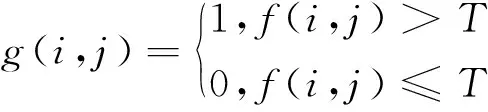
(1)
式中:g(i,j)为该像素点的所属部分,1代表目标区域,0代表背景区域,f(i,j)是指像素点第i行第j列的灰度值,T为阈值。阈值分割以其实现简单、计算量小且性能稳定的特点,在重视运算效率的应用场合得到了广泛的应用。但是,图像分割仍然是一个公认的难题。
1.1 Pawlak粗糙集
粗糙集理论[8]是1982年波兰科学家Pawlak提出的。给定信息系统S=(U,A,V,f),U为论域,A为属性集,V为值域,f:U×A→V为信息函数。设属性B⊆A和集合X⊆U,则可以在属性B下用集合X的上下近似来近似模拟X。X的下近似和上近似分别定义为:

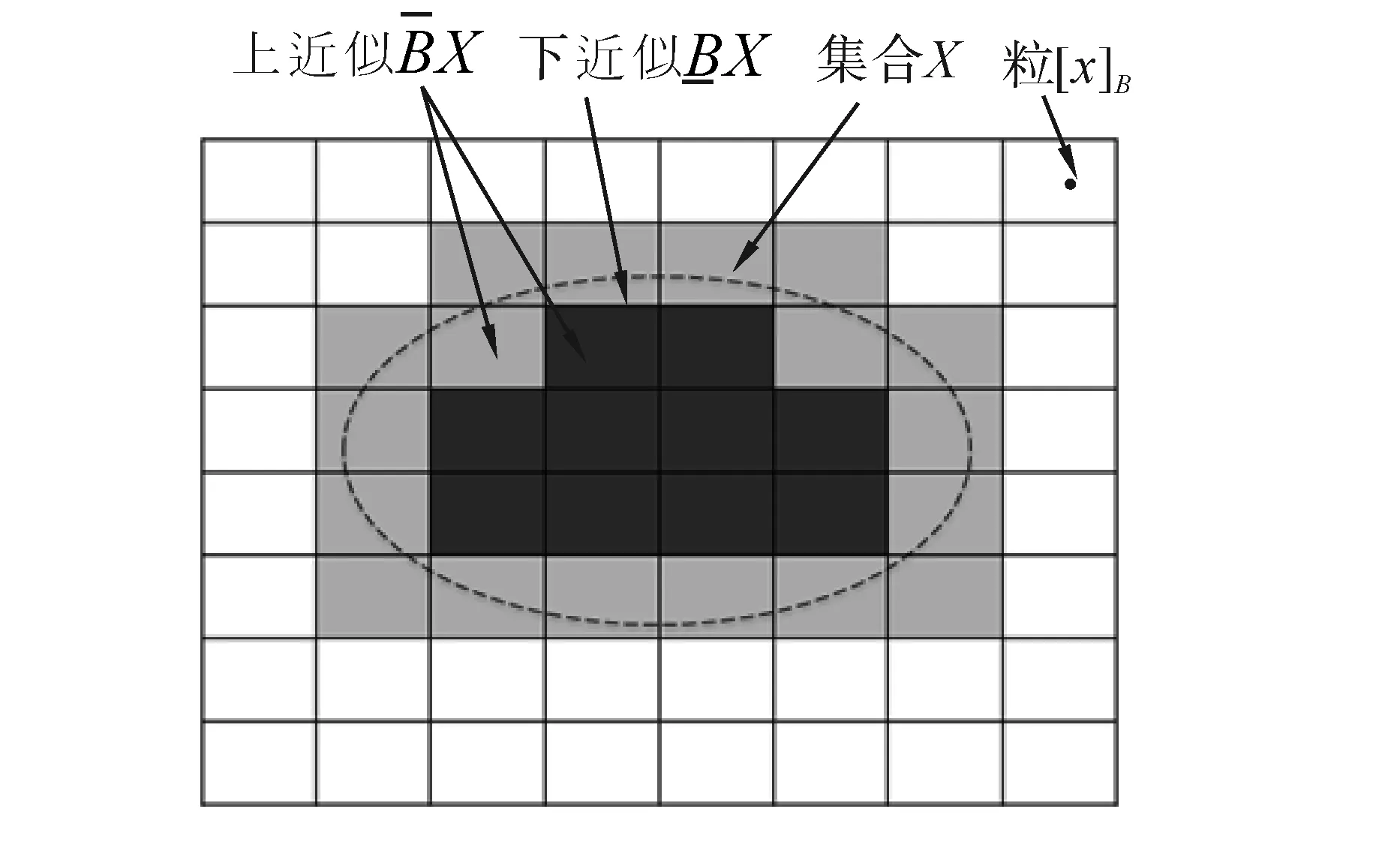
图1 集合X的上近似、下近似示意图Fig.1 The upper and lower approximations of set X
基于X的上、下近似,可以得到论域U的一个划分,分别定义为X的正域POS(X)、负域NEG(X)和边界域BND(X):

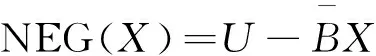

由此可知,如果x∈POS(X),则x一定属于X;如果x∈NEG(X),则x一定不属于X,即属于X的补集Xc;如果x∈BND(X),则不能判断x一定属于或者不属于X。
1.2 决策粗糙集
由于Pawlak粗糙集模型使用绝对集合包含关系来定义上、下近似,对于带有噪声的数据不能很好地处理。在文献[9]中,Wong和Ziarkao将概率近似空间引入到粗糙集的研究中。令Pr(X|[x])表示等价类[x]中元素属于X的条件概率。那么,可以得到粗糙集的另一种等价表示:
Pr(X|[x])=1⟺[x]⊆X
Pr(X|[x])=0⟺[x]∩X=∅
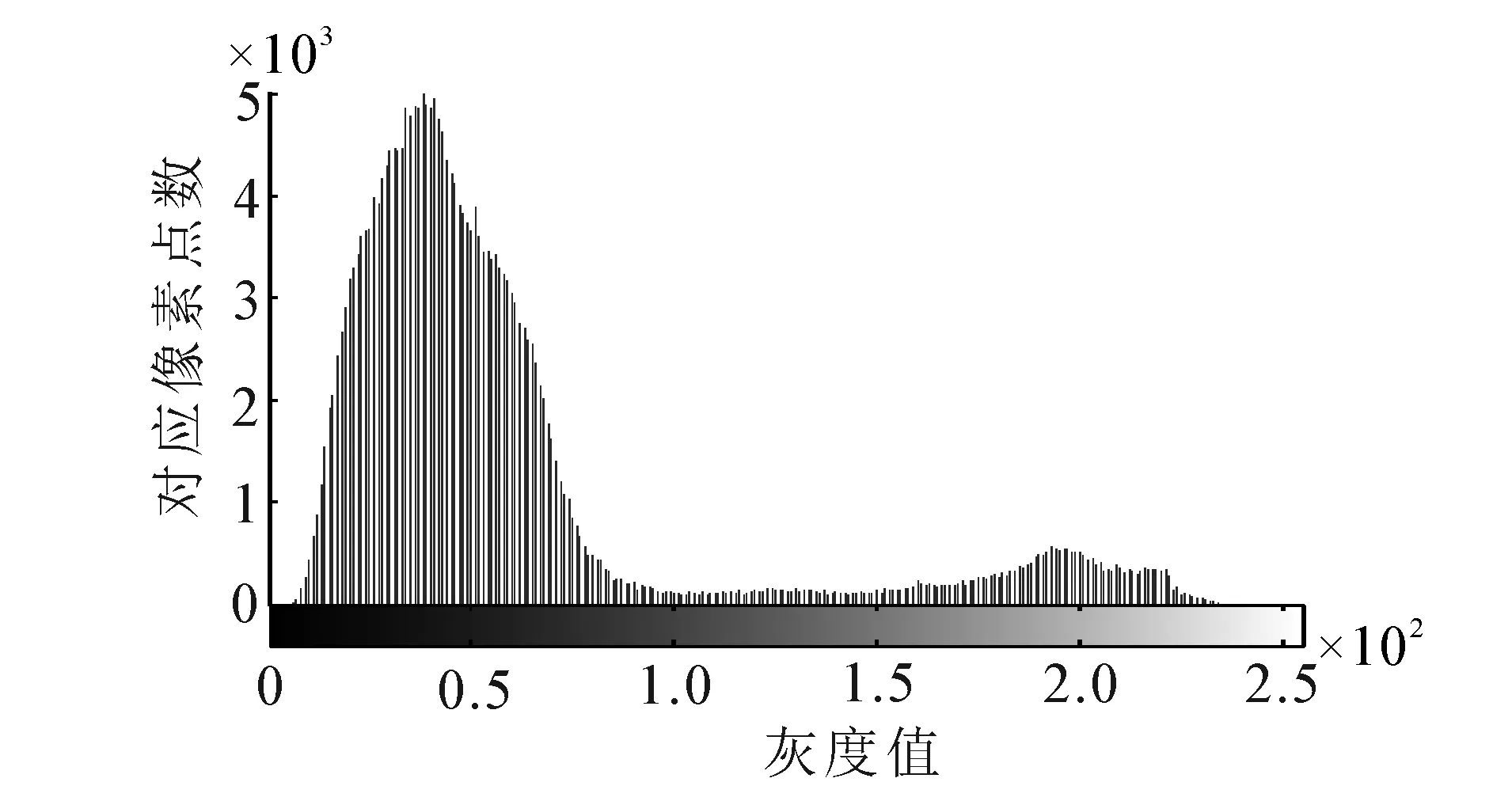
0 则粗糙集中的3个域可以有另一种表示: 这样,定性粗糙集3个域仅用了概率的2个极端值,即0和1。如果将0和1用其他的值来表示,就可以获得一种定量粗糙集。 在1990年,Yao等在文献[10]中提出了一个更一般性的概率粗糙集模型,称为决策粗糙集模型。该模型用一对概率阈值来定义概率正、负和边界域。设0≤β≤α≤1,决策粗糙集模型的一个基本结果是(α,β)-概率正、负和边界域: 同Pawlak的3个域相比,α和β分别取代了概率极值1和0。为了表示集合X在B下的不确定程度,粗糙度R的定义被提出,即: (2) 当粗糙度为0时,X在B下是精确的,即是一个精确集;而当粗糙度大于0时,X在B下是模糊不可辨的,是一个粗糙集。关于粗糙集更多详细的介绍可以参见文献[6]。 在图像分割的过程中,图像中的所有像素点构成论域U,将一幅图像划分成大小为m×n个重叠的块,每个块被看成是一个粒G。那么,每个粒中有m×n个像素点。定义粒后,图像中的目标区域就可以用粗糙集思想来模拟,即目标区域的上下近似可以分别看成内部含有的最大粒簇和外部包含他的最小粒簇。 本文处理的是二值化灰度图像,即将图像分割成目标区域B和背景区域O两部分。假设整幅图像的灰度级为L,只要找到一个最好的阈值T,就能将图像分成B(0,1,…,T)和O(T+1,T+2,…,L-1) 2类。这样就可以得到目标区域和背景区域的上、下近似,分别表示为 式中:g(j,k)是粒Gi中像素点调用式(1)后的结果。因为做的是二值化,图像中除了目标区域便是背景区域,背景也就是目标的补集,每个粒的像素点个数为mn,那么背景的正域便是目标的负域,因此可得: (3) 可以看出,对于属于目标(背景)下近似的粒,严格要求粒中的所有像素点的灰度值必须大于(小于)阈值T。此类式子对于没有噪声的图像分割效果很好,但是在实际中有一些图像带有噪声,对于这类带有噪声(如高斯噪声)的图像处理效果却不尽人意,因为此类图像几乎找不到属于下近似的粒,没有办法进行处理。 为了更好地处理带有噪声的图像,因此将决策粗糙集的思想引入到图像分割中,允许一些噪声点的存在,这样定义目标的上下近似时,概率阈值不再是{0,1},而是{1-α,α}(α∈[0.5,1]),于是从式(3)得到新的定义公式: 再根据式(2)就能得到目标和背景的粗糙度: (4) 式中:|·|表示集合的基,即集合元素的个数。这里定义图像的粗糙熵: (5) 文献[2]中指出,当粗糙熵最大时,取得最优的分割阈值T,即T*=argmaxRET。当熵取得最大值时,粗糙度也降到最低,取得最好的分类效果。 假设max_gray和min_gray分别表示图像中最大的灰度级值和最小的灰度级值。图像划分成大小为m×n的粒Gi,粒的总数用total_num表示 分别表示目标和背景的上、下近似,ROT、RBT则分别表示目标和背景的粗糙度,RET表示粗糙熵。 初始化:置 为空集 1)fori=1 to total_num *对所有的图像粒Gi进行如下操作*初始化Ni为0 forj=1 tomn *计算该粒中大于阈值T的像素点个数Ni* if the gray ofj>T Ni=Ni+1 end end ifNi/mn≥α else end ifNi/mn≤1-α else end end 2)forL=min_gray to max_gray *对所有图像灰度级进行如下操作*在进行运算前先调用 1) 根据式(4)分别得到在阈值L下目标和背景的粗糙度ROT(L)和RBT(L)。再根据式(5)计算出相应的粗糙熵RET(L)。 end 3)当粗糙熵值取得最大时图像分割阈值取得最优值,即: 本文所提出的方法是在文献[2]的基础上做出的改进,能很好地处理带噪声的图像,所以为了验证本文方法的优势,分别用文献[2]中的方法和本文所提出的方法去处理带噪声的图像,并进行了实验对比。 要完成图像分割最优阈值的选择,首先需要的是将图像划分成一簇尺寸大小相等的粒,而粒的大小的选取影响着最终分割的效果。这里依据图像的灰度直方图,选取直方图中各峰值对应的区域宽度中最小值的一半作为粒的长和宽[2]。选的太大会出现漏判目标区域为背景区域的情况,而选的太小则会把一些不必要的区域误判为目标区域,增加算法复杂度。粒的尺寸变大(变小)会使求出的最佳阈值T减小(增大)。 实验选取了文献[2]实验中的块图片(BLOCKS),并对其进行了尺寸变换(变换为512×512和加噪声(椒盐噪声)处理,然后用本文提出的方法和文献[2]提出的方法分别进行处理,并比较最终的实验结果,即最后阈值的选择情况和分割效果。 首先是选择粒的尺寸,图片的灰度直方图如图2所示,只要选择峰值对应区域宽度最小值的一半作为粒的长宽是最合适的。图2中峰值对应区域最小的部分为180和220之间,即最小宽度为40,这样将图像划分成20×20的粒群是最合适的。 图2 灰度直方图Fig.2 Histogram of the image 图像划分完成后,分别按本文前面所提算法和文献[2]中所提方法进行实验,这里参数α取0.05,参数α的取值是根据经验和多次实验迭代而来。实验结果如图3所示。 图3(b)的阈值选择结果在预期之中,如前面所讲,按文献[2]方法很难让下近似不为0,导致所求的阈值无意义,根本起不到分类的效果。针对这个问题,实验还选取了其他一些图片,同样进行加噪处理后,得到的阈值结果也为254,所以这个方法处理带噪声的图片是不行的。 而本文的方法则有相对较好的结果,在处理带噪声的图片时,允许粒中部分像素点为噪点,不会影响分割效果。而且在得到二值化的图像后,再进行去噪,也简单方便许多。所以在处理带噪声的图片上,本文的方法是比较可行的。 (a)加噪声原始图片 (b)T=254[2] (c)本文方法结果(T=104)图3 实验结果Fig.3 Experimental results 当前已有的大部分图像分割方法都是针对不带噪声图像提出的,然而实际生活中的图像常常是存在噪声的。为了较好地解决带噪声的图像分割问题,本文利用粗糙集方法模拟图像的目标和背景区域,提出了一种基于决策粗糙集的图像分割方法。实验结果表明,该方法在处理带噪声的图像分割问题中能够取得较理想的效果,并简化了以往处理带噪声图像的过程。在本文提出的方法中,如何进行参数α选取是一个较困难的问题,接下来的工作是如何寻找一种高效地选取参数α的方法。 参考文献: [1]SEZGIN M, SANKUR B. Survey over image thresholding techniques and quantitative performance evaluation[J]. Journal of Electronic Imaging, 2004, 13(1): 146-165. [2]PAL S K, SHANKAR B U, MITRA P. Granular computing, rough entropy and object extraction[J]. Pattern Recognition Letters, 2005, 26(16): 2509-2517. [3]CHAKRABORTY D, SHANKAR B U, PAL S K. Granulation, rough entropy and spatiotemporal moving object detection[J]. Applied Soft Computing, 2013, 13(9): 4001-4009. [8]PAWLAK Z. Rough sets[J]. International Journal of Computer and Information Science, 1982(11): 341-356. [9]WONG S K M, ZIARKO W. Comparison of the probabilistic approximate classification and the fuzzy set model[J]. Fuzzy Sets and Systems, 1987, 21: 357-362. [10]YAO Y Y, WONG S K M, LINGRAS P. A decision-theoretic rough set model[C]//Proceedings of the 5th International Symposium on Methodologies for Intelligent Systems, Knoxville, USA, 1990 : 17-25.
2 基于决策粗糙集的图像分割
2.1 图像的粗糙集描述

2.2 阈值最优选择算法
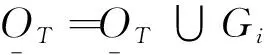

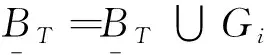
3 实验分析
3.1 粒尺寸的大小选择
3.2 实验结果
3.3 结果分析


4 结束语

