基于倾斜角的多目标测向无源定位技术

汪望松，修建娟，修建华

（海军航空工程学院信息融合研究所，山东烟台264001）

基于倾斜角的多目标测向无源定位技术

汪望松，修建娟，修建华

（海军航空工程学院信息融合研究所，山东烟台264001）

对多目标测向无源定位问题进行了研究。虽然无源观测站不同，针对同一目标的方位角和俯仰角数据也不同，但它们有共同的倾斜角。基于此，提出了基于倾斜角的多目标测向无源定位算法。该算法分别计算一组与多个目标对应的倾斜角，然后利用倾斜角最接近原则对这2组数据进行关联判断，解决多目标测向数据的关联和定位问题，并通过仿真实验，对算法的有效性和可行性进行了验证。

倾斜角；无源定位；数据关联；多目标跟踪

由于无源定位系统本身不发射信号，只是被动接收目标发射、反射或散射信号，因而具备较强的抗干扰、抗反辐射导弹、抗低空突防和反隐身能力[1-3]。在现代电子战日趋激烈的今天，无源定位系统生存能力较强，具备其他传感器所无法替代的优势，因而受到世界各国的普遍重视。但由于无源传感器不能直接测量目标的距离信息，因而在无源探测方式下欲获得目标状态的良好估计也是比较困难的[4-5]。目前较常用的无源定位方法中多站测向定位是运用较多的一种[6-8]，它通过高精度的测向设备在2个不同观测点对目标进行测向，2个测向线的交点就是目标的位置。当监视区域内存在多个目标时，2个观测站不同的测向线相交将产生大量的虚假定位点（鬼点），采用3个以上的观测站对目标进行测向交叉定位虽然可以有效排除鬼点，但此方法的计算量随着观测站和目标数量的增多而呈指数增长，数据关联的难度大[9-10]。为此，这里在2站情况下基于倾斜角方法[11]对多目标测向无源定位问题进行了研究，并给出了相应的定位算法。该算法在同一坐标系中分别计算2个无源观测站与多个目标对应的倾斜角，然后利用倾斜角最接近原则对这2组数据进行关联判断，解决多目标测向数据的关联和定位问题，最后通过仿真实验对算法的有效性和可行性进行了验证。

1 倾斜角定义

无源传感器对目标的测量信息有方位角和俯仰角，如图1所示α和β。设无源观测站获得的目标方位角和俯仰角数据是以该观测站为原点的坐标系下的数据，并假设坐标系以正北方向为y轴，正东方向为x轴，无源观测站正上方为z轴。

图1 无源观测站坐标示意图Fig.1 Schematic diagram of passive sensor coordinate

在坐标系中无源观测站不同，针对同一目标的方位角和俯仰角数据也不同，见图2，α1≠α2，β1≠β2。

图2 2部无源观测站坐标示意图Fig.2 Schematic diagram of two passive sensors coordinate

利用2个观测站测量的方位角和俯仰角就可计算出目标的位置坐标：

再利用一个精度高的观测站的俯仰角，就可计算出高度。

观测站1的测量俯仰角的精度高为

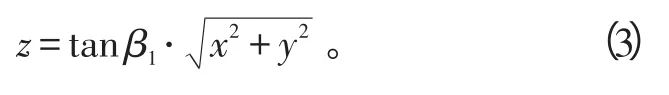
观测站2的测量俯仰角的精度高为

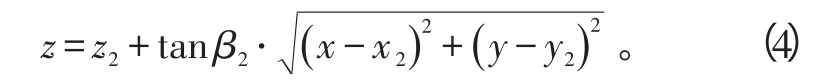
考虑到多站测向无源定位中虚假定位点排除所带来的问题以及系统的复杂性，这里考虑另一种利用倾斜角进行无源定位的方法。虽然无源观测站不同，针对同一目标的方位角和俯仰角数据也不同，但它们有共同的倾斜角[11]，下面首先看一下倾斜角的定义。假定2个无源观测站处于同一高度时，确定一个参考平面，该参考平面经过2个无源观测站站且平行于水平面，如图3所示。

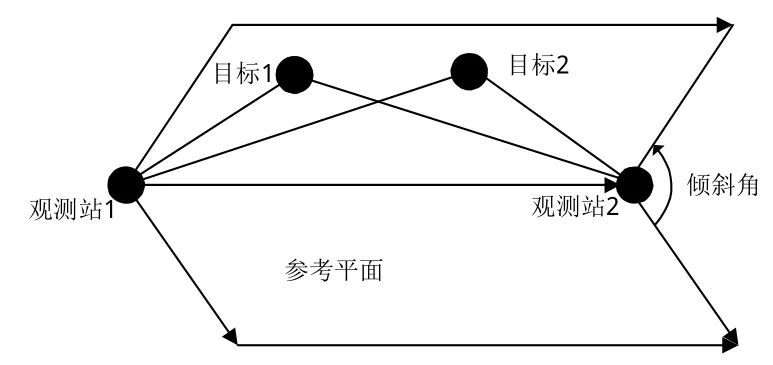
图3 2部无源观测站处于同一高度时的参考平面图Fig.3 Reference plan with two same altitude sensors

图3中，无源观测站1和无源观测站2以及目标确定的平面与参考平面的夹角即是倾斜角。当站1、站2与目标1目标2共面，则目标1、2的倾斜角相同，无法区分2目标，此时不能用倾斜角方法进行定位，该情况这里不考虑。

若2部无源观测站1、2处于不同高度，分别在A点和B点。建立坐标系：以正北方向为y轴，正东方向为x轴，z轴垂直于水平面，观测站1所在的A点为原点，如图4所示。选参考平面为AB连线与过该直线上一点且方向为正北方向的直线构成的平面ABN，ATB构成另一个平面，其中T为目标点，T′为T在参考平面上的投影。则参考平面ABN与平面ATB之间的夹角即为倾斜角θ。这里φ为参考平面ABN与水平面AB′N之间的夹角，B′为B点在A点所在水平面AB′N上的投影，d为过垂直水平面的平面AB′B与平行于正北方向且垂直水平面的平面即平面AYZ之间的夹角。当2个观测站的位置固定后，φ和d的值也就是定值了，不因坐标系不同而不同。

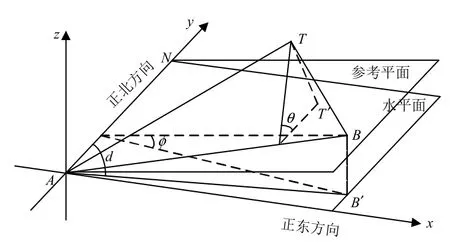
图4 2部无源观测站处于不同高度时的参考平面图Fig.4 Reference plan with two different altitude sensors

首先计算φ和d，设观测站2的坐标为(x2,y2,z2)，则可求得：

由文献[11]可知，对观测站1可求得倾斜角θ有

由式（6）可看出，倾斜角的公式完全与目标径向距离信息无关，它只与测得的目标方位角α、俯仰角β、以及平面交角φ和d有关，式（6）的限制条件是目标不能在2个无源观测站的基线或其延长线的正上空。

对于无源观测站2可用同样的方法求得倾斜角。

2 基于倾斜角的多目标数据关联

步骤1：

1

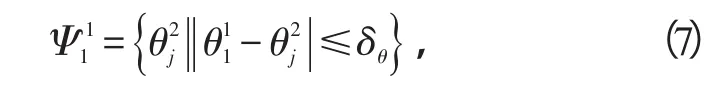
式中，δθ为关联门限，其与角度测量误差的大小有关；

标对应的倾斜角，并将其赋予集合Γ1；

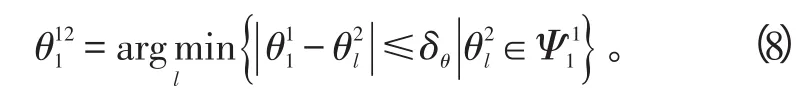
步骤2：

1）同理，以Θ1中的第二个元素为中心，按照步骤1给出的方法对集合Θ2中的各元素做出选择；

步骤3：

，则分以下2种情况：

步骤4：

同理，以集合Θ1中的其余元素为中心，按照步骤1～步骤3对集合Θ2中的各元素做出选择；在集合Θ1中的各个元素均完成关联判断后，将集合Θ2中的未关联上的元素赋予集合Γ2；此时集合Θ1和Θ2中各元素分为以下情况：

1）集合Θ1和Θ2中部分倾斜角元素关联成功，构成一对一的关联对，利用和这些倾斜角对应的方位角和俯仰角测量数据由式（1）～（3）或（4）即可确定目标位置；

2）集合Θ1和Θ2中未关联成功的倾斜角数据（集合Γ1和Γ2中的元素），可能是和虚假目标相对应的倾斜角数据，也可能是由于其中某个无源传感器漏检造成的关联不成功，此时如果有第3个无源观测站的数据（与前2个观测站在一条直线上）可利用，则可利用第3个无源观测站的倾斜角数据对集合Γ1和Γ2中的元素作进一步判断。

3 仿真分析

以2个观测站对2个目标进行观测为例，以观测站1为基准，采样间隔t=1 s，对2个目标跟踪100 s，进行100次蒙特卡洛仿真。

3.1 测角精度对算法性能的影响

观测站1的坐标为原点，观测站2的坐标为(30 000,20 000,1 000)，目标在的初始位置为(60 000,70 000,10 000)的1km内随机产生，航向随机，航速在100～350 m/s之间随机，测角精度分别为0.1°和0.5°时，仿真结果如图5～8所示。

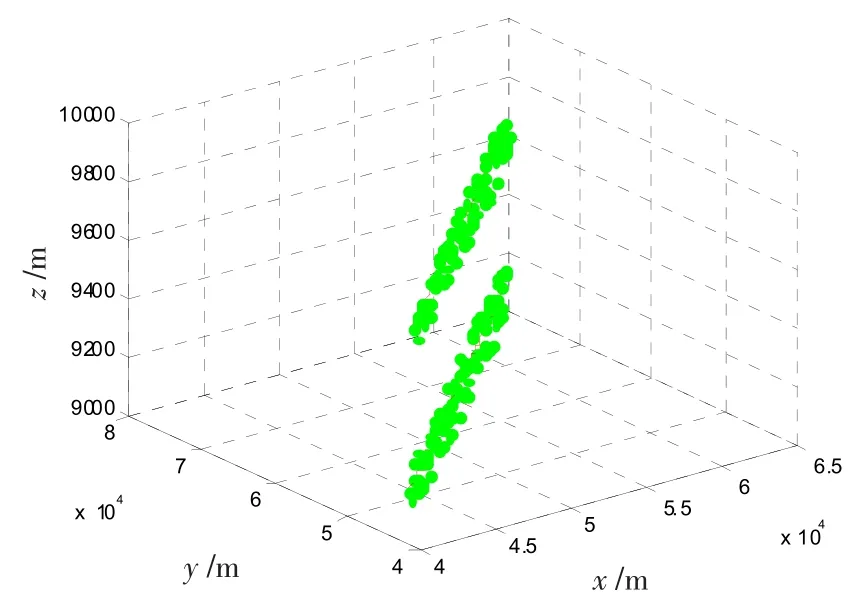
图5 跟踪曲线（测角精度0.1°）Fig.5 Tracking curve（measuring precision of angle is0.1°）

图6 均方根误差曲线（测角精度0.1°）Fig.6 RMS error（measuring precision of angle is0.1°）

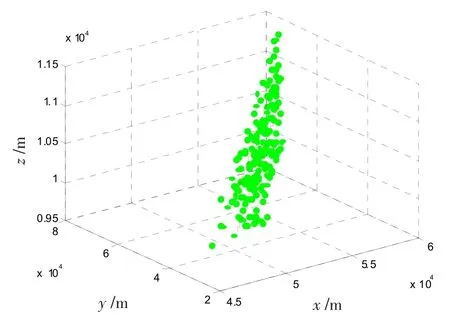
图7 跟踪曲线（测角精度0.5°）Fig.7 Tracking curve（measuring precision of angle is0.5°）

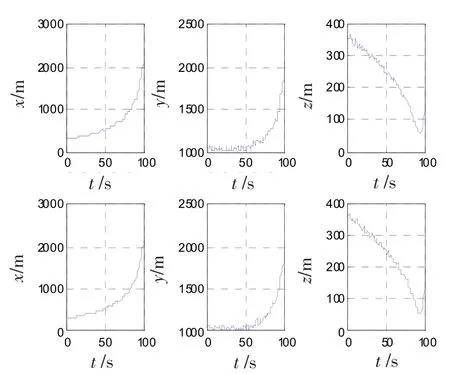
图8 均方根误差曲线（测角精度0.5°）Fig.8 RMS error（measuring precision of angle is0.5°）

由上面2幅图对比可知，测角精度对目标的跟踪效果影响较大，精度越差，均方根误差也就越大，目标跟踪效果也就越差，若精度更差，算法甚至失效。

3.2 2站的高度差对算法性能的影响

观测站2的坐标分别为(30 000,20 000,0)、(30 000,20 000,5 000)，即2站的高度差分别为0 m和5 km时，其他条件同3.1，仿真结果见图9、10（2站高度差0 m）和图11、12（2站高度差5 km）。

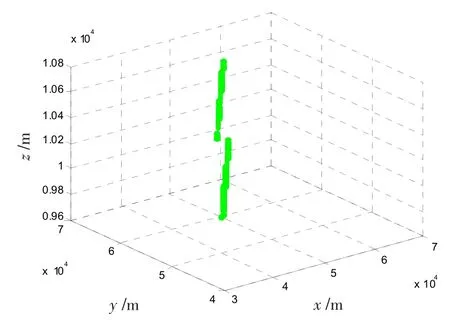
图9 跟踪曲线Fig.9 Tracking curve

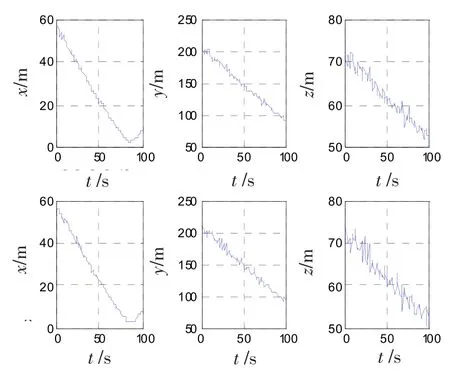
图10 均方根误差曲线Fig.10 RMS error

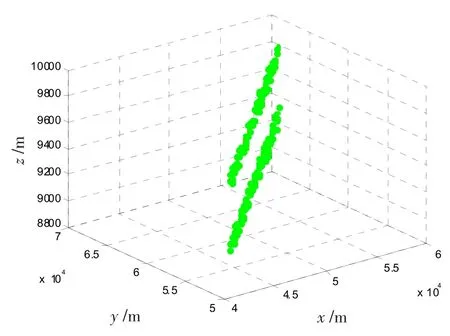
图11 跟踪曲线Fig.11 Tracking curve

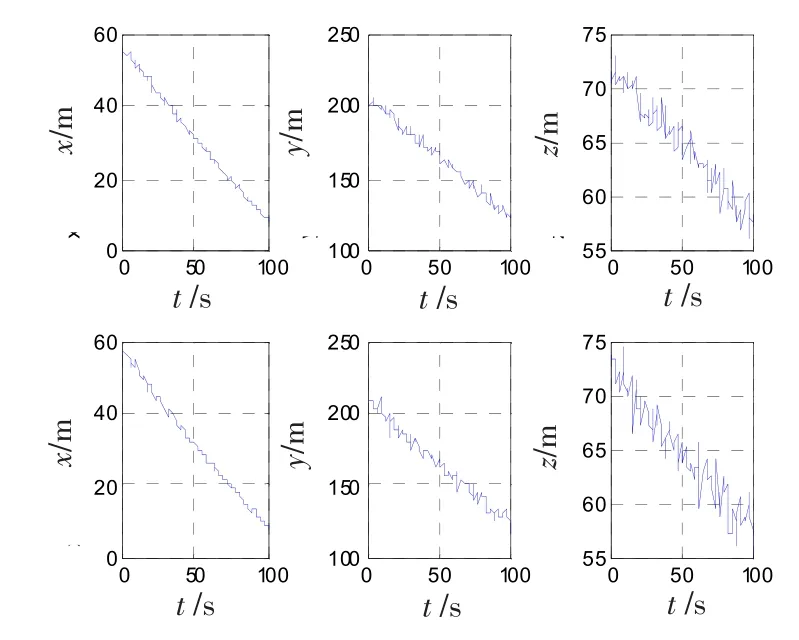
图12 均方根误差曲线Fig.12 RMS error

对比上面2幅图以及图5、图6（2观测站的高度差为1km），可以得出高度差对目标跟踪效果的影响比较小。因而该方法对布站的海拔高度选择要求就没有那么苛刻，可以利用空中和地面观测站布站。

3.3 观测站之间的距离远近对算法性能的影响

假设观测站2的位置为(20 000,20 000,1 000)，其他同3.1，仿真结果如图13、14所示：

图13 跟踪曲线Fig.13 Tracking curve

图14 均方根误差曲线Fig.14 RMS error

对比图5和图6可得出，改变2个无源观测站之间的相对位置，对目标观测的影响不大。因此，可以利用车载或舰艇上的观测设备灵活机动布站。

4 结论

从本文的仿真结果和分析可得知，利用倾斜角的方法可以有效地对目标进行跟踪。而当目标在2个观测站的基线或其延长线的上空运动时，2观测站倾斜角的方法就失效了，可以通过利用多个传感器布站成多边形同时观测来解决上述问题。该方法对观测站之间高度、距离的要求不高，可以利用机载、舰载、车载和地面固定观测站灵活搭配观测。现实中可以利用无源传感器的组网布站，调整观测站之间的距离、方位，合理利用倾斜角方法对目标进行跟踪。

[1]何友，修建娟，关欣.雷达数据处理及应用[M].3版.北京：电子工业出版社，2013：257-259. HE YOU，XIU JIANJUAN，GUAN XIN.Radar data processing with applications[M].3rd ed.Beijing：Publishing House of Electronics Industry，2013：257-259.（in Chinese）

[2]夏佩伦.目标跟踪与信息融合[M].北京：国防工业出版社，2010：186-192. XIA PEILUN.Target tracking and information fusion[M]. Beijing：National Defense Industry Press，2010：186-192.（in Chinese）

[3]权太范.目标跟踪新理论与技术[M].北京：国防工业出版社，2009：310-315. QUAN TAIFAN.New theory and technical about target tracking[M].Beijing：National Defence Industry Press，2009：310-315.（in Chinese）

[4]WANG G H，BAI J，HE Y，et al.Optimal deployment of multiple passive sensors in the sense of minimum concentration ellipse[J].IET Proceedings on Radar，Sonar& Navigation，2009，3（1）：8-17.

[5]XIU JIANJUAN，HE YOU，WANG GUOHONG.Constellation of multisensors in bearing-only location system [J].IEE Proceedings on Radar，Sonar&Navigation，2005，152（3）：215-218.

[6]BAI JING，WANG GUOHONG，KONG MIN，et al. Study on data association methods for distributed passive sensors with long baseline[J].Chinese Journal of Electronics，2009，18（2）：270-274.

[7]DARKO MUSICKI.Bearing only multi-sensor maneuvering target tracking[J].Systems Control Letters，2008，57（3）：216-221.

[8]刘晓飞.分布式无源定位系统信息融合技术研究[D].成都：西南交通大学，2008. LIU XIAOFEI.Research on information fusion techniquesofdistributedpassivelocationsystem[D]. Chengdu：Southwest Jiaotong University，2008.（in Chinese）

[9]DARKO MUSICKI.Multi-target tracking using multiple passive bearings-only asynchronous sensors[J].IEEE Transactions on Aerospace and Electronic Systems，2008，44（3）：1151-1160.

[10]陈玲，陈德煌.多站无源定位系统中的机动目标跟踪算法[J].电讯技术，2010，50（10）：10-14. CHEN LING，CHEN DEHUANG.Maneuvering target tacking algorithm in multi-passive location system[J]. Telecommunication Engineering，2010，50（10）：10-14.（in Chinese）

[11]宋军，王国宏.倾斜角定位技术的研究[J].舰船电子工程，2005，25（2）：5-11. SONG JUN，WANG GUOHONG.Study on the passive location with inclination angle[J].Ship Electronic Engineering，2005，25（2）：5-11.（in Chinese）

TN953

A

2014-02-21；

2014-03-20

“泰山学者”建设工程专项经费资助项目

汪望松（1983-），男，硕士。

1673-1522（2014）03-0275-05

10.7682/j.issn.1673-1522.2014.03.016