基于PⅠDNN变结构理论的新型弹道导弹姿控系统设计

袁钢，施建洪，李瑞涛

（1.海军装备部，上海200436；2.海军航空工程学院控制工程系，山东烟台264001）

基于PⅠDNN变结构理论的新型弹道导弹姿控系统设计

袁钢1，施建洪2，李瑞涛2

（1.海军装备部，上海200436；2.海军航空工程学院控制工程系，山东烟台264001）

针对新型弹道导弹参数及干扰的随机变化性，研究了姿控系统的设计问题。首先，对被控对象的模型进行了描述，使模型的确定量和不确定量相分离；其次，在不确定上界已知的假设下，完成了变结构控制器的设计；再次，在不确定上界未知的假设下，将比例—积分—微分神经网络（PIDNN）理论与变结构理论相结合，利用PIDNN对模型的不确定上界进行估计，完成了PIDNN变结构控制器的设计，并通过Lyapunov稳定性理论对系统的稳定性进行了证明；最后，通过仿真分析，验证了所设计方法的有效性。

新型弹道导弹；不确定上界；变结构控制；比例—积分—微分神经网络

新型弹道导弹的气动特性具有静不稳定性，也就是说，若没有姿态控制系统，导弹不能稳定飞行，很小的扰动就会使导弹翻滚。要使这种导弹稳定飞行，必须有相应的姿态控制系统。

杨泽生、徐延万[1]针对弹道导弹的弹性振动的抑制、外部干扰的补偿等具体问题，探讨了变结构自适应理论在姿态控制系统设计中的应用。他们提出了不确定边界的自适应估值算法和基于简化模型的变结构自适应控制器设计，并对设计的姿态控制系统进行了仿真，仿真结果显示采用变结构方法设计的姿态控制系统比采用经典理论设计的姿态控制系统具有更强的鲁棒性和较高的精确度。相关研究成果还有自适应时变滑模控制器[2]、新型终端滑模姿态控制[3]、积分滑模姿态控制[4]，张义捷[5]、白辰[6]、周连文[7]进一步将模糊理论引入到姿态控制系统的设计过程中。姚红[8]、王芳[9]采用H∞鲁棒控制方法进行了姿控系统定点控制器的设计，能够基本满足姿态控制的要求。鲁棒控制的优点在于抑制干扰和补偿未建模动态。但是鲁棒控制没有学习的能力，在设计时要求知道不确定性的上界值，这就造成它的设计过于保守，系统的稳定是以增加控制器的保守性为代价的。

比例—积分—微分神经网络（PIDNN）是舒怀林教授[10]于1997年提出的，它将静态神经元扩充到动态神经元，进而构成了一种具有动态特性的神经网络，具有结构简单、收敛速度快的特点以及任意精度的非线性逼近能力，在系统辨识、控制等很多领域表现出了很高的应用价值。

本文将变结构理论[11-13]与PIDNN相结合，提出了一种PIDNN变结构控制器的设计方法，用PIDNN对模型不确定上界进行估计，进而基于变结构理论进行控制器设计，最终设计的控制器对参数变化及随机干扰具有很好的适应性，而且可以保证很高的控制精度。

1 姿控系统设计

1.1 被控对象的描述

固体导弹姿态控制具有运动参数的时变性、参数及扰动的随机变化性、控制对象及设备的严重非线性以及弹性振动等特性，因而要得到其精确模型是不可能的。这里的不确定量主要包括参数的不确定性和外界的扰动（视弹体的弹性运动为扰动量），新型弹道导弹三通道模型可表示为：

式（1）中：φ、ψ、γ为导弹飞行姿态角；φ˙、ψ˙、γ˙为导弹飞行姿态角速度；φ¨、ψ¨、γ¨为导弹飞行姿态角加速度；b1、b2、b3、d3为模型的已知系数；Δb1、Δb2、Δb3、Δd3为未确定系数；fd1、fd2、fd3为干扰信号；δφ、δψ、δγ为俯仰、偏航、滚转通道的控制输入。

进一步整理可得到：

式（2）中：ρ1、ρ2、ρ3为不确定项，

从式（2）可以看出，俯仰通道的运动方程具有最一般的结构形式，因而以俯仰通道为例进行研究具有一般性，将其描述为

式中：b＞0；u为输入；fd为外加的干扰信号。

将式（3）改写为

假设1：M和由确定和不确定2部分组成，即其中，Mn和为确定量，ΔM和为不确定量。

结合假设1，式（5）进一步变为

1.2 上界已知时变结构控制器的设计

式中，φ¨d为期望的俯仰角加速度。

将滑模面定义为

对式（8）求导，得到

令s˙=0，则有

下面对所设计的控制器进行稳定性分析。

选取Lyapunov函数为

求导，并将式（7）和式（9）代入，得到

将式（10）代入式（12），整理得到

系统的稳定性得证。

1.3 基于PⅠDNN上界自适应学习的变结构控制器设计

在不确定上界未知的情况下，选取单个比例—积分—微分神经网络（SPIDNN）作为学习网络，这是一个3层前向神经元网络，为2×3×1结构，其输入层有2个神经元，接受外部输入信息；它的隐含层有3个神经元，分别为比例元、积分元和微分元，完成比例、积分和微分运算；它的输出层只有1个神经元，完成控制规律的综合和输出，其结构如图1所示。

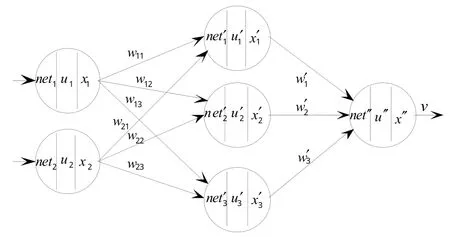
图1 单个比例—积分—微分神经网络的结构形式Fig.1 Structure of SPIDNN

在任意时刻t，对神经元网络的第j个神经元，其总输入netj等于与其相连的各支路输出量x1,x2,…,xn分别乘上权重值w1j,w2j,…,wnj后的总和，即：

神经元的状态uj由此神经元的状态转换函数g(·)决定。用神经元当前输入netj和当前状态为自变量，按其状态函数就可产生神经元的下一个状态，即，其中，θj为神经元的阈值，本文的计算中均设阈值为0。

神经元的输出xj由此神经元的输出函数f(·)决定，用神经元状态uj为自变量，按其输出函数就可产生神经元的输出值，即xj(k)=f(uj(t))。

这里采用Sigmoid函数，其表达式为

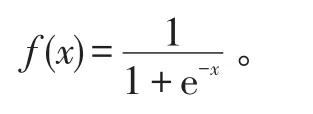
SPIDNN的输入层有2个神经元，在任意采样时刻k，其输入neti(k)=ri(k),i=1,2，输入层神经元的状态为ui(k)=neti(k),i=1,2，输入层神经元的输出为

隐含层是神经元网络中最重要的层次，SPIDNN的隐含层有3个神经元，分别为比例元、积分元和微分元，它们各自的输入总值均为

式中：wij为输入层至隐含层的连接权重值；上标“′”为隐含层变量标记。

输出层结构比较简单，它只包含一个神经元，完成网络的总和输出功能，其总输入为

式中：x′j为隐含层各神经元的输出值；w′j为隐含层至输出层的连接权重值。

输出层神经元的状态函数与比例元的状态函数相同，状态为u″(k)=net″(k)。

输出层神经元的输出函数与网络中其他神经元的输出函数相同，输出为

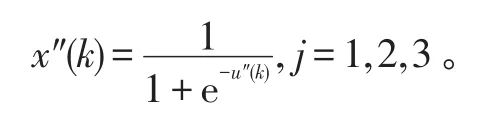
SPIDNN的输出v(k)就等于输出层神经元的输出，即

固定输入层至隐含层的权值ωij(i=1,2;j=1,2,3)，仅调节隐含层至输出层的权值，记，将网络的输入设定，输出为不确定参数上界的估计值，有，其中，为隐含层的输出，是连续系统的积分，在离散系统中代表累加，而是微分符号，在离散系统中代表差分。

上节中的变结构控制律变为利用PIDNN的逼近引理[10]，可做出如下假设。

假设2：PIDNN的最优权值向量ω*满足：

最优权值向量的元素；ε1为已知正常数。

假设3：不确定参数的上界满足：

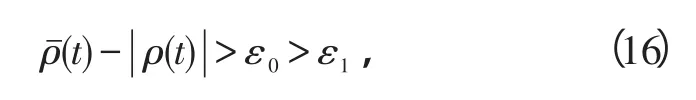
式中，ε0为已知正常数。

采用自适应算法在线调整权值，取：

选取Lyapunov函数为

式（19）两边对时间求导，并结合式（12）得到

将式（14）代入式（20），得到

通过加减项处理，得到

将式（17）、式（18）代入式（22），得到

结合假设2和假设3，最终得到

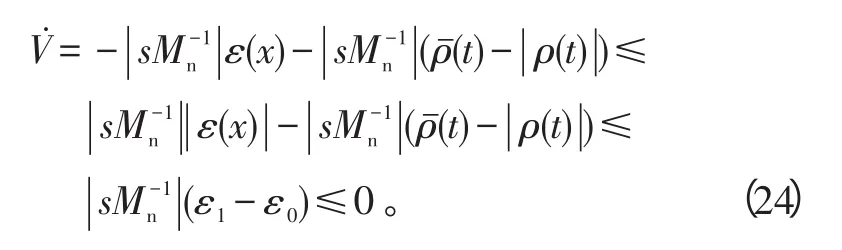
因此，控制系统的稳定性得证。

综上可得如下结论。

2 仿真分析

取b1=0.1，b2=-14.6，b3=14，Δb1=0.05sin(2πt)，Δb2=4sin(2πt)，Δb3=2cos(2πt)，fd=0.5sin(πt)，为了抑制颤振，用来代替sgn(s)。

仿真结果如图2所示。

图2 状态量及控制输入的变化情况Fig.2 Change condition of state variables and control input

从图2 a）中可以看出，所设计的控制器能够在很短的时间内将姿态角误差和姿态角速度误差控制到零，对参数变化及随机干扰具有很好的适应性，而经典控制方法则对参数和随机干扰有严格的要求，只有在其裕度范围内才能保证系统的稳定，而且响应速度慢，如果采用经典控制理论对式（25）所示的模型进行控制器设计，由于参数摄动范围过大（通常情况下摄动范围在±25%以内），将导致系统不稳定，图2 b）给出的控制输入曲线光滑有界，满足控制要求。

3 结束语

本文以弹道导弹三通道姿态运动的动力学模型为研究对象，在不确定上界已知的情况下，完成了变结构控制器的设计；在不确定上界未知的情况下，将PIDNN理论与变结构控制理论相结合，利用PIDNN对系统的不确定上界进行估计，完成了PIDNN变结构控制器的设计，并通过Lyapunov稳定性理论对姿控系统的稳定性进行了证明；最后，进行了仿真分析，仿真结果证明了所设计方法的有效性。

[1]杨泽生，徐延万.变结构自适应控制理论在运载火箭姿控系统设计中的应用[J].航天控制，1997，15（4）：9-16. YANG ZESHENG，XU YANWANG.Application of variable structure system adaptive control theory in launch vehicle attitude system design[J].Aerospace Control，1997，15（4）：9-16.（in Chinese）

[2]王亮，刘向东，盛永智.基于高阶滑模观测器的自适应时变滑模再入姿态控制[J].控制与决策，2014，29（2）：281-286. WANG LIANG，LIU XIANGDONG，SHENG YONGZHI.High-order sliding mode observer based adaptive time-varying sliding mode for re-entry attitude control[J]. Control and Desion，2014，29（2）：281-286.（in Chinese）

[3]胡庆雷，姜博严，石钟.基于新型终端滑模的航天器执行器故障容错姿态控制[J].航空学报，2014，35（1）：249-258. HU QINLEI，JIANG BOYAN，SHI ZHONG.Novel terminal sliding mode based fault tolerant attitude control for spacecraft under actuator faults[J].Acta Aeronautica et Astronautica Sinica，2014，35（1）：249-258.（in Chinese）

[4]耿洁，刘向东，盛永智，等.飞行器再入段最优自适应积分滑模姿态控制[J].宇航学报，2013，34（9）：1215-1223. GENG JIE，LIU XIANGDONG，SHENG YONGZHI，et al.Optimal adaptive integral sliding mode control for reentry vehicle attitude[J].Journal of Astronautics，2013，34（9）：1215-1223.（in Chinese）

[5]张义捷，钟友武，许得军.基于模糊控制技术的飞行器姿态控制系统设计[J].航天控制，2013，31（2）：28-32. ZHANG YIJIE，ZHONG YOUWU，XU DEJUN.The aerocraft attitude control system design based on fuzzy logic control[J].Aerospace Control，2013，31（2）：28-32.（in Chinese）

[6]白辰，任章，樊垚，等.基于模糊神经网络扰动观测器的RLV动态逆再入姿态控制[J].中南大学学报：自然科学版，2013，44（增刊1）：58-62. BAI CHEN，REN ZHANG，FAN YAO，et al.Dynamic inversion control for RLV reentry attitude based on fuzzyneural disturbance observer[J].Journal of Central South University：Science and Technology，2013，44（S1）：58-62.（in Chinese）

[7]周连文，李芳华.基于自适应模糊滑模的飞行器姿态控制系统设计[J].航天控制，2013，31（5）：13-18. ZHOU LIANWEN，LI FANGHUA.Design of aircraft attitude control system based on adaptive fuzzy sliding mode[J].Aerospace Control，2013，31（5）：13-18.（in Chinese）

[8]姚红.固体弹道导弹鲁棒及自适应姿态控制系统设计研究[D].长沙：国防科技大学，2006：54-59. YAO HONG.Research on robust and adaptive attitude control system design of solid-propellant ballistic missile [D].Changsha：National University of Defense Technology，2006：54-59.（in Chinese）

[9]王芳，宗群，田栢苓，等.基于鲁棒自适应反步的可重复使用飞行器再入姿态控制[J].控制与决策，2014，29（1）：12-18. WANG FANG，ZONG QUN，TIAN BAILING，et al.Robust adaptive back-stepping flight control design for reentry RLV[J].Control and Design，2014，29（1）：12-18.（in Chinese）

[10]舒怀林.PID神经元网络及其控制系统[M].北京：国防工业出版社，2006：76-79. SHU HUAILIN.PID neural networks and control systems [M].Beijing：National Defense and Industry Press，2006：76-79.（in Chinese）

[11]BARTOSZEWICZ A，PATTON R J.Sliding mode control [J].International Journal of Adaptive Control and Signal Processing，2007，21（8）：635-637.

[12]YOUNG K D，UTKIN V I，OZGUNER U.A control engineer’s guide to sliding mode control[J].IEEE Transactions on Control Systems Technology，1999，7（3）：328-342.

[13]PERRUQUETTI W，BARBOT J P.Sliding mode control in engineering[M].Boca Raton：CRC Press，2002：232-234.

Design of Attitude Control System for New Ballistic Missiles Based on PIDNN Variable Structure Control Theory

YUAN Gang1,SHI Jian-hong2,LI Rui-tao2
（1.Naval Equipment Department,Shanghai 200436,China; 2.Department of Control Engineering,NAAU,Yantai Shandong 264001,China）

The design problem of attitude control system for new ballistic missiles was studied to deal with the uncertainty of parameters and disturbance.Firstly,the model of the object was described to separate certain and uncertain parameters. Secondly,variable structure controller was designed on the assumption that upper bound of uncertainties was known. Thirdly,on the assumption that upper bound of uncertainties was unknown,PIDNN variable structure controller was designed by integrating variable structure control theory with PIDNN theory which was used to estimate the upper bound of uncertainties and the stability of the system was proved by Lyapunov theory.Finally,the simulation was presented to demonstrate the effectiveness of the proposed method.

new ballistic missiles;upper bound of uncertainty;variable structure control;PIDNN

TJ765.2+3

A

2014-03-01；

2014-04-01

袁钢（1974-），男，工程师，硕士。

1673-1522（2014）03-0225-05

10.7682/j.issn.1673-1522.2014.03.006