脉冲随机微分系统的均方指数稳定性分析

陈涵，杨树杰，牟朝霞

（海军航空工程学院a.研究生管理大队；b.基础部；c.军事教育与训练系，山东烟台264001）

脉冲随机微分系统的均方指数稳定性分析

陈涵a，杨树杰b，牟朝霞c

（海军航空工程学院a.研究生管理大队；b.基础部；c.军事教育与训练系，山东烟台264001）

研究了脉冲随机时滞微分泛函方程的均方指数稳定性问题。利用Lyapunov-Razumikhin型方法及随机分析的一些技巧，建立了一类脉冲随机泛函微分方程的均方指数稳定性定理。

脉冲随机微分方程；均方指数稳定；Lyapunov-Krasovskii函数

近年来，脉冲泛函微分系统（IFDSs）的稳定性的问题吸引着越来越多的学者在理论和实际应用方面的研究[1-3]，特别是在针对IFDS指数稳定性方面的研究，并且建立了一些相应的稳定性理论。但随机扰动在现实系统中也是不可避免的，随机模型在自然科学和工程领域的许多分支中正扮演着重要的角色。近几年，脉冲随机微分系统（ISDSs）稳定性分析和脉冲随机泛函微分系统的镇定性问题引起了学者们的广泛兴趣[4-14]。文献[10]利用了一些微积分不等式和随机分析的技巧，而非借助Lyapunov-Razumikhin方法研究了一类带有混合时滞的脉冲随机切换系统的均方指数稳定性。文献[4]利用数学分析方法和泛函Razumikhin方法，建立了基于Lyapunov-Krasovskii函数的一类IFDSs的均方稳定的充分性判据。受到上述文献的启发，并借助于其Lyapunov方法和随机分析的技巧，本文进一步探究了此类IFDSs的指数稳定性问题，得到了系统指数稳定的充分性判据。然而，根据作者所知，目前大部分学者对脉冲随机泛函微分方程指数稳定性的研究，都是借助于Lyapunov函数V(t,φ)在脉冲点处左右极限的一些对应关系来探究系统的稳定性问题的[12，14]。本文直接利用系统状态x(t)在脉冲点处左右极限的关系研究一类脉冲随机泛函微分系统的稳定性问题，建立了不同于文献[12]的指数稳定判定定理。

1 引理和记号

还需要如下引理。

引理1：[15]（Chaplygin比较定理）假定f,F∈C()G，如果分别是两个初值问题的解，则对所有对于所有的

2 脉冲随机时滞系统的均方指数稳定性判定定理

2.1 主要问题及定义

考虑如下脉冲随机时滞泛函系统的均方指数稳定性问题：

下面将分2种情况考虑系统（1）的均方指数稳定问题。

定义1：对于任意可容许的脉冲时刻序列N，系统（1）的解称为均方指数稳定的，是指存在一个常数λ＞0且对任意的ε＞0，都存在常数δ=δ(ε)＞0，使得对任意的初值函数，对于任意t≥t0，都有

定义2：[2]称函数属于V(1,2)，如果：

2）V(t,x)关于x是局部Lipschitz的；

3）对任意k=1,2,…，以下极限存在且有限：，且

2.2 脉冲随机时滞系统的均方指数稳定判定定理

定理1：假定存在常数b＞a＞0，λτ＞0，β＞0，及Lyapunov-Krasovskii函数，使得以下条件成立：，则系统（1）关于脉冲集是均方指数稳定的。

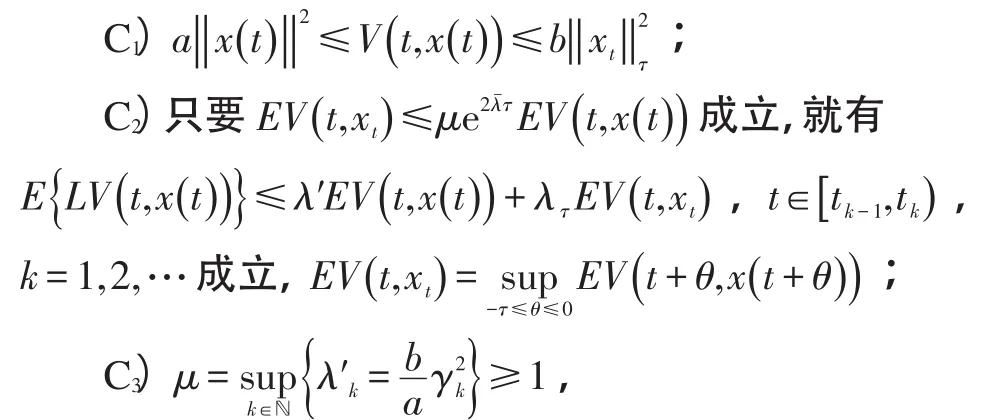
证明：对任意给定的ε＞0，选取假定初值函数，并记系统（1）通过()t0,φ的解对于，根据公式，对于t≠tk，k=1,2,…，有

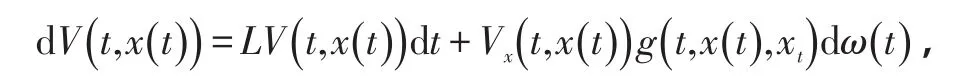
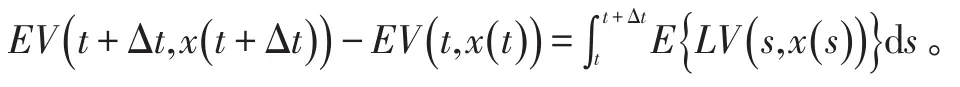
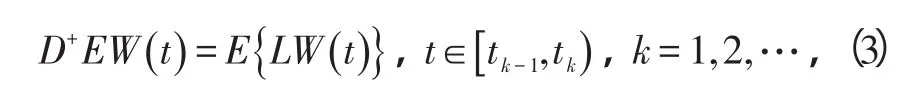
式中，

因此只需证明，对任意t∈(t0,t1)，式（5）成立即可。如果不成立，则一定存在s∈(t0,t1)，使得

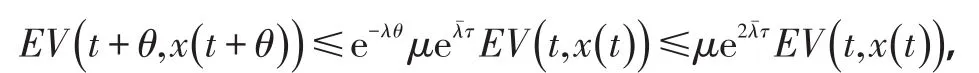
结合式（3）、（4）及条件C2）、C3），对，有

这就与式（8）及（9）矛盾，假设不成立，从而式（5）成立。

于是需要考虑以下2种情形。

（11）成立。于是根据条件C3），式（5）及引理1，得到

这就与假设矛盾。

由式（1）、（2）及（12）有：

如果用条件D1）代替定理1中的条件C1），则得到如下结果。

定理2：假定存在常数b＞a＞0、λτ＞0、β＞0、及Lyapunov-Krasovskii函数，使得条件：D1）、C2）及C3）成立，则系统（1）对任意脉冲序列Ninf(β)是均方指数稳定的。

证明：证明方法类似于定理1，故略去。证毕。

注1：对比定理1和定理2，可发现系统（1）的均方指数稳定性受到函数V(t,x(t))中时滞的影响。

注2：当μ≥1时，脉冲可能破坏稳定性，所以需要脉冲发生得不要太频繁，即脉冲间距要比较大。

条件C1）成立；

D2）：只要成立，就有成立，则：

证明：证明结论Ⅰ），Ⅱ）的证明与Ⅰ）类似，故略去。

考虑到μ＜1，故存在充分小的常数使

现在要证明式（5）在(t0,t1)成立。否则，存在s∈(t0,t1)，使得式（7）成立。

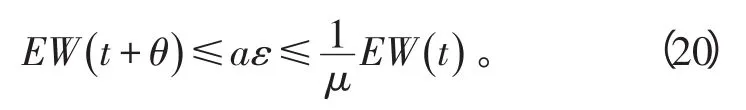
进而得到

再由条件D2），意味着对

由引理1，式（19）、（21）及D3）有

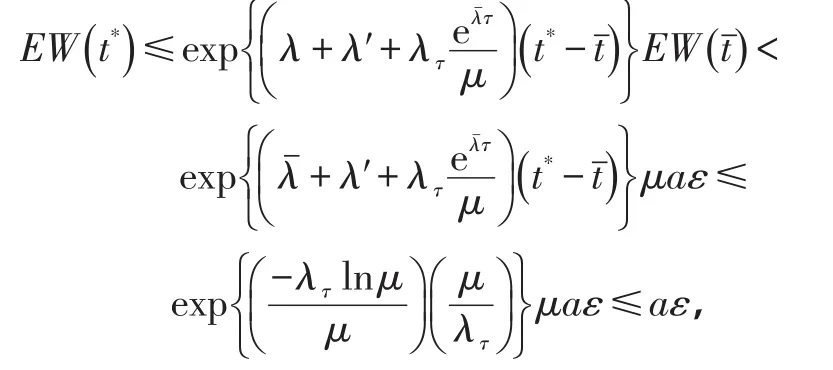
这就与式（18）矛盾。

事实上，根据式（1）、（2）、（16）条件C1）和D3），有

3 结论

本文研究了一类脉冲随机泛函微分系统的均方指数稳定性问题。利用Lyapunov函数和Razumikhin型方法，建立了系统均方指数稳定的充分性判据。本文为了方便，仅讨论了系统的均方指数稳定性，其结果可以推广到p阶矩指数稳定性上来。

[1]GOPALSAMY K，ZHANG B.On delay differential equations with impulses[J].Journal of Mathematical Analysis andApplications，1989，139：100-122.

[2]STAMOVA I，STAMOV G.Lyapunov-Razumikhin method for impulsive functional equations and applications to the population dynamic[J].Journal of Computational and Applied Mathematics，2001，130：163-171.

[3]NAGHSHTABRIZI P，HESPANHAJ.Exponential stability of impulsive systems with application to uncertain sampled-date systems[J].Systems and Control Letters，2008，57：378-385.

[4]YANG S J，SHI B，LI M.Mean square stability of impulsive stochastic differential systems[J/OL].International JournalofDifferentialEquations.Doi:10.1155/2211/ 613695.2011.

[5]YANG J，ZHONG S M.Mean square stability analysis of impulsive stochastic differential equations with delay[J]. Journal of Computational and Applied mathematics，2008，216：474-483.

[6]LIU X，BALLINGER G.Uniform asymptotic stability of impulsive delay differential equations[J].Computers and Mathematics withApplications，2011，41：903-915.

[7]WANG Q，LIU X.Impulsive stabilization of delay differential systems via the Lyapunov-Razumikhin method[J]. Applied Mathematics Letters，2007，20：839-845.

[8]FU X L，LIU D.Razumikhin-type theorems on exponential stability of impulsive infinite delay differential sys-tems[J].Journal of Computational and Applied mathematics，2009，224：1-10.

[9]ZHU Q X，SONG B.Exponential stability of impulsive nonlinear stochastic differential equations with mixed delays[J].Nonlinear Analysis：Real World Applications，2011，12：2851-2860.

[10]XU L G，HE D H.Mean square exponential stability analysis of impulsive stochastic switched systems with mixed delays[J].Computers and Mathematics with Applications，2011，62：109-117.

[11]XU L G，HE D H，MA Q.Impulsive stabilization of stochastic differential equations with time delays[J].Mathematics and Computer Modelling，2013，57：997-1004.

[12]LIU J，LIU X Z，XIE W C.Impulsive stabilization of stochastic functional differential equations[J].Applied Mathematics Letters，2011，24：264-269.

[13]CHENG P，DENG F Q，YAO F Q.Exponential stability analysis of impulsive stochastic functional differential systems with delayed impulses[J].Communications in Nonlinear Science and Numerical Simulation，2014，19：2104-2114.

[14]WU X T，ZHANG W B，TANG Y.pth Moment stability of impulsive stochastic delay differential systems with Markovian switching[J].Communications in Nonlinear Science and Numerical Simulation，2013，18：870-1879.

[15]时宝，张德存，盖明久.微分方程理论及其应用[M].北京：国防工业出版社，2005：40-41. SHI BAO，ZHANG DECUN，GAI MINGJIU.Theory and applications of differential equations[M].Beijng：National Defense Industry Press，2005：40-41.（in Chinese）

Mean Square Exponential Stability Analysiss of Pulse Randomly Differential Systemss

CHEN Hana,YANG Shu-jieb,MU Zhao-xiac
（Naval Aeronautical ang Astronautical University a.Graduate Students’Brigade; b.Department of Basic Sciences;c.Department of Military Education and Training,Yantai Shandong 264001,China）

In this paper,the mean square exponential stability analysis of impulsive stochastic functional differential systems with delays was concerned.On the basis of the Lyapunov-Razumikhin method and stochastic analysis techniques, some general criteria were established for mean square exponential stability.

pulse randomly differential equation;mean square exponential stability;Lyapunov-Krasovskii function

O175.21

A

2014-03-17；

2014-04-10

陈涵（1991-），男，硕士生。

1673-1522（2014）03-0296-05

10.7682/j.issn.1673-1522.2014.03.020