基于试验与蒙特卡洛法的子母弹子弹落点计算模型

孙少华，李国林，尚雅玲

（海军航空工程学院a.兵器科学与技术系；b.七系，山东烟台264001）

基于试验与蒙特卡洛法的子母弹子弹落点计算模型

孙少华a，李国林b，尚雅玲a

（海军航空工程学院a.兵器科学与技术系；b.七系，山东烟台264001）

针对目前子母弹子弹落点散布计算模型存在不足，影响子母弹毁伤效能评估准确性的问题，提出一种基于试验数据的子弹落点散布计算模型。对子母弹靶场试验数据进行分析处理，根据相邻子弹间距、不同环带中子弹数量的规律，建立了子弹落点散布模型；结合母弹散布，建立了子母弹子弹落点散布计算模型。该模型在给定子母弹散布参数后，可以快速生成群射子母弹子弹群的地面散布，且与实际情况基本相符，为子母弹毁伤效能评估奠定了基础。

子母弹；靶场试验；落点散布；蒙特卡洛法

子母弹以其覆盖面积大，火力密集迅猛等特点，广泛配用于导弹、火箭弹、炮弹、航空炸弹等。为评估子母弹对特定目标的毁伤效能，需要对子母弹子弹落点散布规律进行研究。对于子弹的落点散布，目前多采用蒙特卡洛方法，通过计算机仿真在指定区域如圆、圆环、椭圆或者椭圆环内按照一定分布规律（如均匀分布、正态分布等）随机产生子弹的落点散布[1-5]。这些研究近似模拟了子弹的落点散布，能基本满足子母弹毁伤效能评估的需要。随着弹药技术的发展以及CCW公约（《常规武器公约》）的限制，各种新型子母弹应运而生，它们各自具有不同的参数以及特点，在实际使用中表现出良好的性能，对于它们的落点散布，不能简单应用蒙特卡洛随机方法来产生。根据试验情况来看，计算机仿真方法随机产生的落点散布与实际情况出入较大，不能很好满足新型子母弹效能评估的需要。本文应用子母弹试验中获取的大量样本数据，对数据进行分析处理，建立基于试验数据的子弹落点散布模型，并结合母弹散布，通过该模型可以快速生成子母弹的近似落点散布。

1 子弹落点影响因素分析

子弹从母弹中抛撒后，由于抛撒机构赋予子弹串初始速度和推力，子弹串相互分离；每串子弹中各层子弹初始速度不同，子弹产生相互分离。分离后的子弹飘带和稳旋翼片迅速打开，在飘带和子弹自身结构作用下，经过过渡阶段不稳定飞行后，子弹以稳定速度向下运动，进入稳定飞行状态。

影响子弹落点的因素主要有2种：一是自然因素；二是各种设计参数。在子母弹结构定型的前提下，通常考虑下面一些因素。

1）自然条件。发射时的自然条件，如温度、湿度以及风力等气象条件，这些因素对落点分布有着重要的影响，需要在发射装定时进行修正。

2）母弹开舱点参数，包括开舱高度、开舱点处母弹外弹道倾角和攻角、开舱点处母弹的存速。开舱高度不同，子弹在空中的运动时间也会明显变化，从而对落点分布造成明显影响；开舱点处母弹外弹道倾角和攻角，这2个因素会对子弹抛撒的初始状态产生影响从而影响子弹的落点散布；开舱点处母弹的存速，由发射药量、射角以及射向决定。发射药量改变，发射压力即膛压也会随之改变，从而改变了子母弹飞行的动力，造成初速的不同，一般情况下，根据作战需要，发射药量是提前确定的。通过对不同射角试验数据的对比分析，可以发现不同射角时子弹抛撒速度并不相同，这是由于母弹弹体在抛撒过程中所受到的空气动力、力矩的差异以及重力的影响而产生的。

3）子弹药抛撒参数，包括抛撒方向和抛撒速度。抛撒方向根据弹种以及抛撒方式的不同，主要有前抛（例如122 mm火箭炮子母弹），横抛（例如70 km远程火箭炮子母弹），后抛（例如155 mm加榴炮子母弹）3种方式；抛撒速度由母弹存速以及抛撒药量决定。

4）子弹药结构参数，包括稳定带参数、战斗部参数、稳定翼片参数和子弹药旋转角速度。其中：稳定带参数，主要有稳定带宽度、长度等；战斗部参数，如冲压孔直径以及倾斜角；稳定翼片参数，如翼片材料、形状等。

5）生产以及装配工艺。生产及装配工艺的影响主要体现在子弹间是套装的，由于必然产生的加工误差，在子弹成串套装时松紧程度不同，套装松的子弹串抛撒时立即分离，套装紧的则分离稍晚，因而造成子弹落点的差异。

2 试验数据预处理

在子母弹试验中获得的开舱抛撒数据以及落点散布数据，为了给进一步分析提供较好的依据和参考，对经合理采样得到的试验数据，需要进行数据预处理，这里主要进行异常值的处理。

所谓异常值是指在一组观测结果中，明显偏离其他值的那个值，且它和其他测量值不属于同一总体。判别某个可疑数据是否为异常值的步骤：仔细检查和分析原始数据的记录、操作方法、实验条件等过程，找出异常值出现的原因并将相应值剔除。此方法称为物理方法；如果上述方法无法做出判断，就采用统计学方法，即给定一个显著水平，即发生概率，一般为1%或5%，并确定一个相应的置信限，凡超出该误差范围的测量值都是小概率事件，造成该误差的值就为异常值，应予以剔除。

根据野点剔除判定的适用分析以及子母弹的落点坐标的特点和子弹的数量，采用莱茵达准则对异常落点数据进行剔除。其原理为：对试验中观察到的n个样本数据x1,x2,…,xn，求出其算术平均值及剩余误差vi=xi-x¯，然后求出其样本方差

判别依据（假设vi服从正态分布）：，则xi相对而言误差较大，应剔除；为正常数据应该保留。

需要注意的是，由于子母弹试验中一般发射多发子母弹，在剔除野弹之前首先应剔除故障弹。所谓野弹是指以正常的姿态与速度着地并引爆，但由于各种偶然因素的作用，其落点与子弹落点整体分布有明显差异的子弹；故障弹是指没有以正常的姿态或速度着地，未能引爆的子母弹。按照设定的母弹作用可靠性指标，生成随机数剔除故障弹后[6]，剔除野弹按下述步骤进行。

1）求出每发母弹中n枚子弹落点的散布中心：

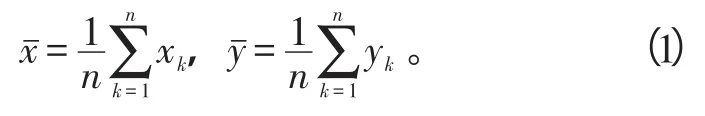
2）求出n枚子弹落点到O的距离di(i=1,2,…,N)及di的均值与样本方差s：

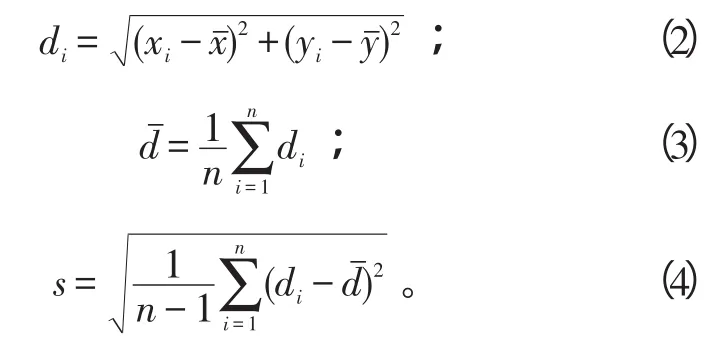
4）若Δdmax≥K·S（一般K取3），则剔除该子弹。

5）重复上述步骤，直至条件Δdmax≥K·S不再满足。

在剔除野弹的时候，剔除子弹总数不能过多，否则，计算结果无法反映子弹开舱抛撒的真实情况。一般情况下，允许剔除子弹的个数应控制在10%之内，若出现较多的野弹或故障弹，则说明该发子母弹抛撒不成功。

3 基于试验数据的子弹群落点散布模型

试验中发射N发母弹，每发母弹里有n枚子弹，第i发母弹的第j枚子弹的落点坐标为(xij,yij)，1≤i≤N，1≤j≤n，假设剔除野弹后第i发母弹中的子弹数为ni，则该枚子弹群落点中心的坐标：

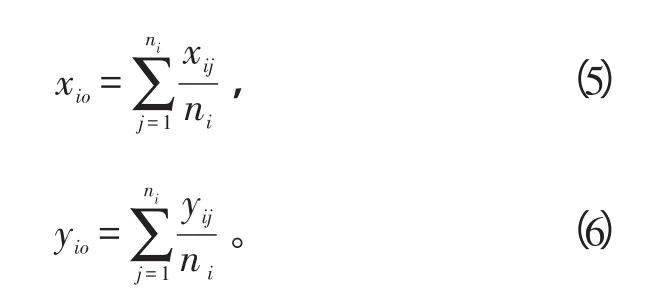
为便于处理，将N发母弹子弹落点试验数据进行处理，经过处理后第i发母弹子弹的落点坐标为：

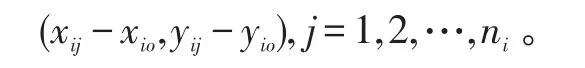
剔除野弹后的N发母弹的所有子弹数为M≤N·n，子弹群落点进行归零化处理后的M枚子弹的落点可以在统一的坐标系中表示。

第j发子弹距离坐标原点的距离为

将dij由小到大进行排序，设dmax=max(dij)。

根据实际需要将dmax划分为n等份，则相邻2个圆环间的距离为

第1环定义为以原点为圆心，以d为半径的圆，第2环定义为以原点为圆心，半径为d与半径为2d的圆所围成的圆环，以此类推，第i环为半径为i-1的圆与半径为i的圆所围成的圆环。假设第i（1≤i≤n)环内的子弹数为φi，则

统计各个相邻圆环间子弹的数量，得到第i发母弹各环中子弹数的数量。对试验中各发母弹的子弹落点数据进行分析，可以得出各发母弹在各环中的子弹数量分布，结果见表1。

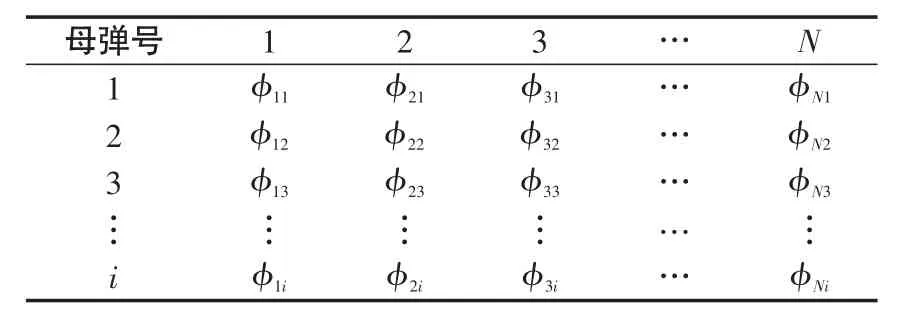
表1 各发母弹子弹在各环内的分布Tab.1 Distribution of submunitions in each circle

使用文献[7]中的方法对数据进行综合处理，建立子弹落点散布参数的计算模型并进行一致性检验。

4 应用实例

4.1 母弹落点的生成

由于母弹的落点散布是由一系列随机干扰因素引起的，这些干扰因素彼此独立，而且每个干扰因素对整体散布的作用微小，根据概率论知识中的中心极限定理可知，这些随机干扰因素产生变量的总和近似服从正态分布[8]。

如不考虑发射时的系统误差，假设母弹开舱高度为固定值，母弹落点(X′,Y′)服从(μx,μy,σx,σy,ρ)二维正态分布。μx、μy分别为母弹落点坐标的均值，即瞄准点(X,Y)，σx=σy=σ为母弹射击精度，ρ为X、Y向的相互关系系数。若坐标轴与主散布轴平行，则射向与侧向散布互相独立，即相关系数ρ=0。母弹落点可由以下随机抽样公式确定：

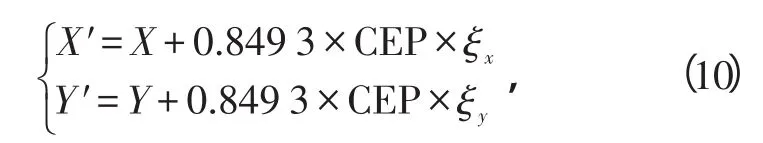
式中，CEP为圆概率误差。

、为标准正态分布的随机数，一般由如下公式产生：

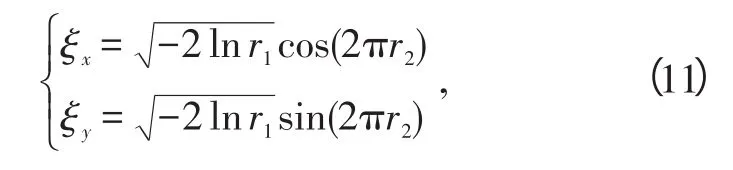
式中，r1、r2为相互独立的均匀随机数，可以利用斐波那契—同余法产生[8]。

使用整体式战斗部的弹箭，通过试验数据可以计算射向（纵向）和横向中间偏差，其CEP可以通过下式进行估算：

4.2 子弹落点的生成

以每发母弹落点为中心，生成该发母弹子弹药的落点散布，每发母弹子弹药的落点生成流程如下：

1）各环内子弹落点。根据子弹在各环内的分布规律，计算各环内子弹落点的数量。

2）确定子弹的坐标。建立极坐标系，见图1。

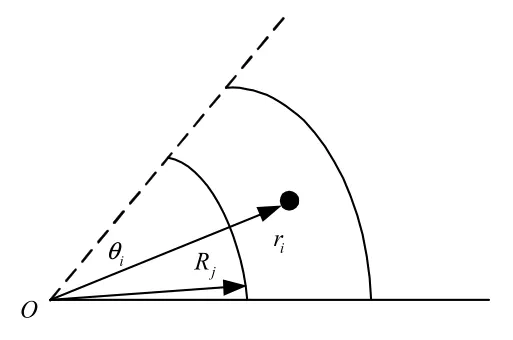
图1 极坐标示意图Fig.1 Schematic diagram of polar coordinate

因子弹落点坐标在各圆环内径向和周向上是均服从均匀分布的，并且是随机的，则第j个环内第i枚子弹的坐标可以表示为：

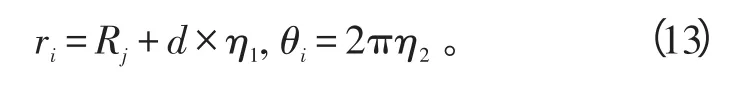
式（13）中：ri表示第i枚子弹落点距离原点的长度；Rj表示该子弹落入第j个环内的起始长度；d表示环距；θi表示第i枚子弹落点的角度；η1、η2表示（0，1）上均匀分布的随机数。

3）子弹的落点坐标统计。根据式（13）的子弹落点随机方程，利用Matlab软件随机产生一发母弹内子弹落点的坐标。

4）重复以上步骤，生成其他（Q-1）发母弹的子弹群落点，并对生成的子弹落点参数与实际试验数据进行对比，如子弹平均间隔，各环带子弹数量分布等，评估子弹落点散布性能。

给定Q=1和n=54，利用子弹药散布模型得到的子弹药散布如图2所示。可以看出，子弹药在射向（X方向）散布为140 m，在侧向（Z向）散布为160 m，子弹药并没有在散布区域内呈现均匀分布或正态分布的特征，大部分子弹基本分布在椭圆环上，且散布中心附近有部分子弹，这与某型子母弹散布情况实际相符，与使用随机数产生的子弹药散布存在明显区别。

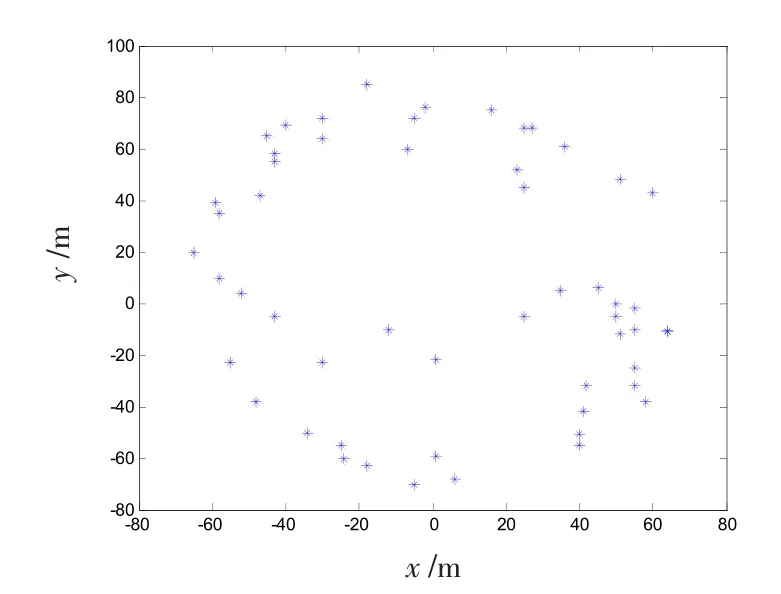
图2 子弹落点散布示意图Fig.2 Schematic diagram of bullet impact dispersion

5 结论

针对子弹药落点生成模型随机性比较大，与实际情况有所不符造成弹药毁伤效能评估结果不准确的问题，本文提出一种基于试验数据拟合的子弹落点散布模型。结合母弹落点的蒙特卡洛生成方法，对子母弹落点情况进行了综合分析。结果表明，该模型可以解决不同参数时的群弹子弹落点散布快速计算问题，且模型所求得落点散布与实际情况基本相符。

[1]孔维红，姜春兰，王在成.某型航空子母弹子弹地面散布研究[J].航空兵器，2005（4）：43-48. KONG WEIHONG，JIANG CHUNLAN，WANG ZAICHENG.Study for bomblets distribution on ground of aerial cluster bomb[J].Aero Weaponry，2005（4）：43-48.（in Chinese）

[2]薛模根，袁宏武，韩裕生，等.侦查评估子弹落点散布仿真研究[J].计算机仿真，2005（11）：46-49. XUE MOGEN，YUAN HONGWU，HAN YUSHENG，et al.Simulation of the dispersion of reconnoitering and evaluating sub-missile’s falling points[J].Computer Simulation，2005（11）：46-49.（in Chinese）

[3]杨世荣，李小强，王才宏.子母弹子弹落点模拟计算方法[J].火力与指挥控制，2008，33（4）：87-90. YANG SHIRONG，LI XIAOQIANG，WANG CAIHONG.Simulated computation method of the cluster warhead’s fall point[J].Fire Control and Command Control，2008，33（4）：87-90.（in Chinese）

[4]孙传杰，卢永刚.一种无控子母弹落点散布分析[J].弹箭与制导学报，2010，30（1）：109-111. SUN CHUANJIE，LU YONGGANG.Analysis of submunition distribution of an unguided cluster munition[J]. Journal of Projectiles，Rockets，Missiles and Guidance，2010，30（1）：109-111.（in Chinese）

[5]王丽珍，吴宏权，张玉忠.子母弹子弹群落点散布椭圆计算方法研究[J].兵器试验，2006（2）：24-28．WANG LIZHEN，WU HONGQUAN，ZHANG YUZHONG.Research on simulation method on ellipse dispersion of submunitions[J].Weapom Test，2006（2）：24-28.（in Chinese）

[6]孙少华，尚雅玲，李国林，等.基于蒙特卡洛方法的制导子弹命中概率模型[J].海军航空工程学院学报[J]. 2013，28（3）：276-280. SUN SHAOHUA，SHANG YALING，LI GUOLIN，et al. Hit probability model of guidance bullet drug based on Mento-Calo method[J].Journal of Naval Aeronautical and Astronautical University，2013，28（3）：276-280.（in Chinese）

[7]中国人民解放军总装备部军事训练教材编辑工作委员会.试验数据的统计分析[M].北京：国防工业出版社，2001：51-67. EDITORIAL BOARD OF MILITARY TRAINNING TEXTBOOK OF PLA GENERAL EQUIPMENT DEPARTMENT.Statistic analysis of experimental data[M]. Beijing：National Defense and Industry Press，2001：51-67.（in Chinese）

[8]王树山，买瑞敏.集束箭弹命中概率分析的蒙特卡洛方法[J].北京理工大学学报，2005，25（4）：286-288. WANG SHUSHAN，MAI RUIMIN.Monte-calo analysis on hit probability of multi-arrow canisters[J].Journal of Beijing Institute of Technology，2005，25（4）：286-288.（in Chinese）

[9]梁剑波，刘新学，王永刚.红外成像末制导子母弹射击效率评定研究[J].航天电子对抗，2007，23（3）：12-14. LIANG JIANBO，LIU XINXUE，WANG YONGGANG. Firing efficiency evaluation of infrared imaging terminal navigation cluster bomb[J].Aerospace Electronic Warfare，2007，23（3）：12-14.（in Chinese）

[10]孙晓峰，吴福强，赵殿善.战术导弹杀伤概率指标检验方法[J].海军航空工程学院学报，2013，28（6）：648-649. SUN XIAOFENG，WU FUQIANG，ZHAO DIANSHAN. Multi-index test method of tactical missile kill probability [J].Journal of Naval Aeronautical and Astronautical University，2013，28（6）：648-649.（inChinese）

TJ413.+3

A

2014-02-20；

2014-03-20

孙少华（1982-），男，博士生。

1673-1522（2014）03-0239-04

10.7682/j.issn.1673-1522.2014.03.009