基于组合预测模型的某型导弹贮存寿命评估方法

徐廷学，奚文骏，赵建印，赵亮

（海军航空工程学院兵器科学与技术系，山东烟台264001）

基于组合预测模型的某型导弹贮存寿命评估方法

徐廷学，奚文骏，赵建印，赵亮

（海军航空工程学院兵器科学与技术系，山东烟台264001）

科学确定导弹的贮存寿命对提高部队装备保障能力和战斗力具有重要的现实意义。针对导弹贮存数据具有“少数据”和随机波动性较大特点，建立了灰色GM(1,1)评估模型和马尔可夫模型的组合预测模型，并应用此组合预测模型解决了某型导弹贮存寿命评估的问题。结果表明，该方法对现有数据拟合程度较好，预测精度较高，克服单一预测方法的不足，有效性强，使用价值大。

灰色—马尔科夫；组合预测模型；导弹贮存寿命评估

导弹作为一次发射使用的产品，从出厂到最后的使用绝大部分时间处于贮存、维修和检测等非工作状态。在贮存过程中会受到来自周围的各种环境应力的影响，从而引起设备的性能参数变化，导致整个系统的功能异常或可靠度降低。因此，导弹贮存寿命评估技术的重要性在于能够得到准确的寿命评估结果，一方面，可以充分发挥导弹装备使用寿命潜力，避免过早报废，充分发挥资源效益；另一方面，能够避免盲目延长使用期可能造成的寿命隐患，提高装备的可用性。因此，导弹贮存寿命评估问题，一直是工业部门和军方非常关注的问题，也是研究中的难题。

国内外已有文献对导弹贮存寿命预测进行相关研究。文献[1-3]介绍了在军用飞机、车辆、电子设备及机械设备领域的寿命预估研究，这些技术是具有代表性且相对成熟的。以美国为代表的西方国家，在电子产品和机械设备中的寿命评估技术已经进入了理论成果应用阶段，大量的寿命评估技术在军事装备智能维护保障技术产品中得到广泛的应用。比较具有代表性的成熟的相关技术产品有：在无人驾驶军用飞机和陆地车辆中使用的低成本气轮发动机诊断/预测系统[4]；应用于F-35联合打击战斗机的机械设备寿命预测PHM（Prognostics and Health Management，PHM）系统等[5]。从这些基于寿命评估技术为核心建立的各种产品应用领域来看，寿命评估技术正朝向系统化、智能化、远程信息化的方向发展。

国内方面，文献[6]采用神经网络的方法，预测一定时间周期内的导弹贮存可靠性；文献[7]以温度为加速应力，采用步进应力加速试验评估某引信的贮存寿命约为17 a；文献[8]采用多模型融合技术和B样条模糊神经网络，建立了寿命预测模型；文献[9]基于贮存可靠度预测模型，提出了一种贮存时间投影估计方法，获得了贮存时间这一关键参数，进而进行贮存寿命分析。

本文针对某型导弹的特点，研究灰色模型、马尔可夫预测模型相结合的方法预测导弹贮存寿命，给出具体的算例，获得计算结果，进一步验证模型、算法的有效性。

1 导弹贮存寿命评估方法研究

所谓导弹贮存寿命评估就是一种分析估算研究导弹贮存寿命的活动，它是通过实验室或现场收集的数据和新的情报，综合考虑各种因素，运用适当的方法和技巧，对对象导弹的贮存寿命进行科学的分析和估算的一种活动[10]。

目前，按照数据获取途径的不同，导弹贮存寿命评估主要有2种基本方法：基于使用监测的方法和基于试验的方法。

基于使用监测的方法是对装备在使用应力水平下的性能参数或失效数据进行监测，通过对监测数据的建模分析实现装备寿命评估。基于寿命试验的方法可以分为常规寿命试验和加速寿命试验的方法。

通过寿命试验的方法得到的数据真实可靠，但周期较长，花费巨大。因此，本文采用基于使用监测的方法对某型导弹进行寿命评估。

基于使用监测的导弹贮存寿命评估方法的核心是评估算法的设计。随着理论基础和科技水平的不断发展，用于装备寿命评估的方法也不断推出，主要包括：专家系统、模糊控制、小波分析、基于灰色理论的方法和人工神经网络理论等方法。若采用单一的方法进行导弹贮存寿命的评估，由于数据量和方法自身的局限性，往往表现出评估结果精确度不足。

为取得较精确的评估结果，本文主要研究灰色—马尔可夫组合评估模型，通过2种模型的有机结合来达到科学预测的目的。灰色—马尔可夫模型是将灰色预测模型与马尔可夫预测方法的优化组合。灰色预测模型能够利用小样本贫信息的数据建立微分方程，预测数据未来发展趋势。马尔可夫则是一种具有无后效性的随机过程，即一个时间序列所处的状态的条件分布只与系统当前时刻所处的状态有关。利用马尔可夫模型的这种特性，修正灰色预测模型的误差，对随机趋势做出估计，可以提高预测精度。

2 灰色—马尔可夫组合预测模型建立

2.1 建GM(1,1)模型，得出原始序列的初步预测值

1）给定序列。设数据样本的时间序列x(0)有n个样本值，的一次累加生成序列，即：

2）建立GM(1,1)模型。假定x(1)序列变化过程呈指数特性，可建立白化微分方程：μ分别为待求发展系数和为灰色系数。

将式离散化，微分方程变为差分方程：

写成矩阵的形式：Y=，向量系数

将由式得到α和μ代入，解得时间响应函数：

3）模型精度检验。为确保所建立的灰色模型应用于评估实践有较高的可信度，一般需要检验模型精度，GM(1,1)模型检验一般有残差检验、后验差检验和关联度检验[11-12]。

利用残差检验方法检验所建模型的精度。

2.2 建立灰色—马尔可夫组合预测模型，得出最终预测值

1）状态划分。根据原始数据序列和GM(1,1)模型的拟合值序列，可以得到残差序列，这是一个具有马尔可夫链特点的非平稳随机序列[13]。为了定义马尔可夫链的状态转移矩阵，将残差序列划分为l个状态。

2）构造状态转移概率矩阵。一般的，第m步状态转移概率矩阵定义如下：

3）对GM(1,1)模型的预测值进行残差修正，建立GM-Markov组合预测模型。根据残差数据以及所确定的状态转移概率矩阵，就可以得出未来的转移状态，也就确定了残差预测值的变动区间，取该区间的中点作为残差预测值，建立GM-Markov组合评估模型，则最终评估模型为：

3 某型导弹贮存寿命评估实例分析

假设某型导弹5 a贮存可靠度数据如表1所示。

表1 某型导弹贮存可靠度数据Tab.1 Storage reliability data of the certain missile

由式（3）～（11）建立GM(1,1)模型，根据此模型结合式（12）得出拟合值序列及残差序列。取l=3，将残差序列划分为3个状态，即表示某一时刻的误差可能增大、减小或保持不变。设残差序列的均值和标准差分别为′，定义区间为状态1，为状态2，为状态

表2 残差状态划分表Tab.2 Partition table of residual state

根据式（15）和式（16）计算出一步状态转移概率矩阵为：

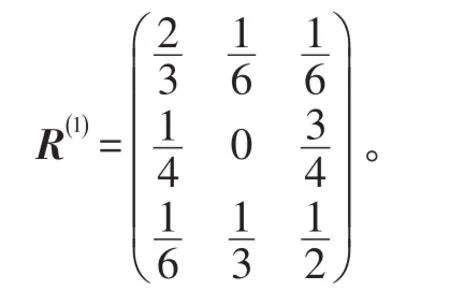
根据数据所处的状态以及得到的状态转移概率矩阵，就可以求出数据的最终预测值，将预测出来的某型导弹贮存可靠度数据与实际值比较，见表3、图1。

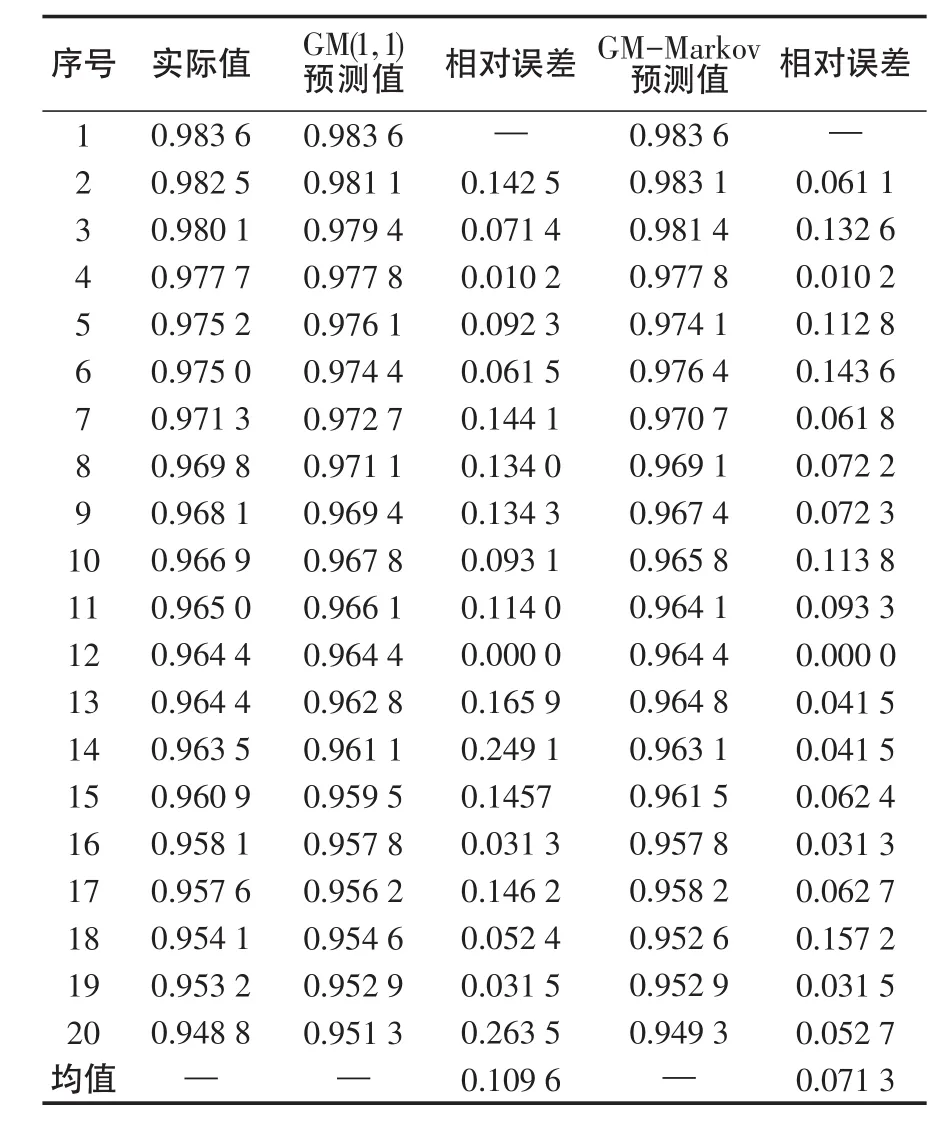
表3 2种方法预测值与实际值比较Tab.3 Comparison of the two methods predicted value and actual value

图1 2种模型预测值与实际值的比较Fig.1 Comparison of the two models predicted value and actual value

从图1中可以看出灰色GM(1,1)模型的预测曲线是一条较平滑的直线，不能反映出数据的波动性，不适用于对具有波动性的数据进行预测，GM-Markov预测模型相对误差小，预测精度很高，拟合程度很好。

用GM-Markov预测模型对某型导弹的贮存可靠度水平进行预测，结果见表4。对表4的预测结果进行多项式拟合，见图2。由图2可知，导弹在12.91 a时的贮存可靠度降低到0.9，所以，可以认为某型导弹的贮存寿命为12.91 a。

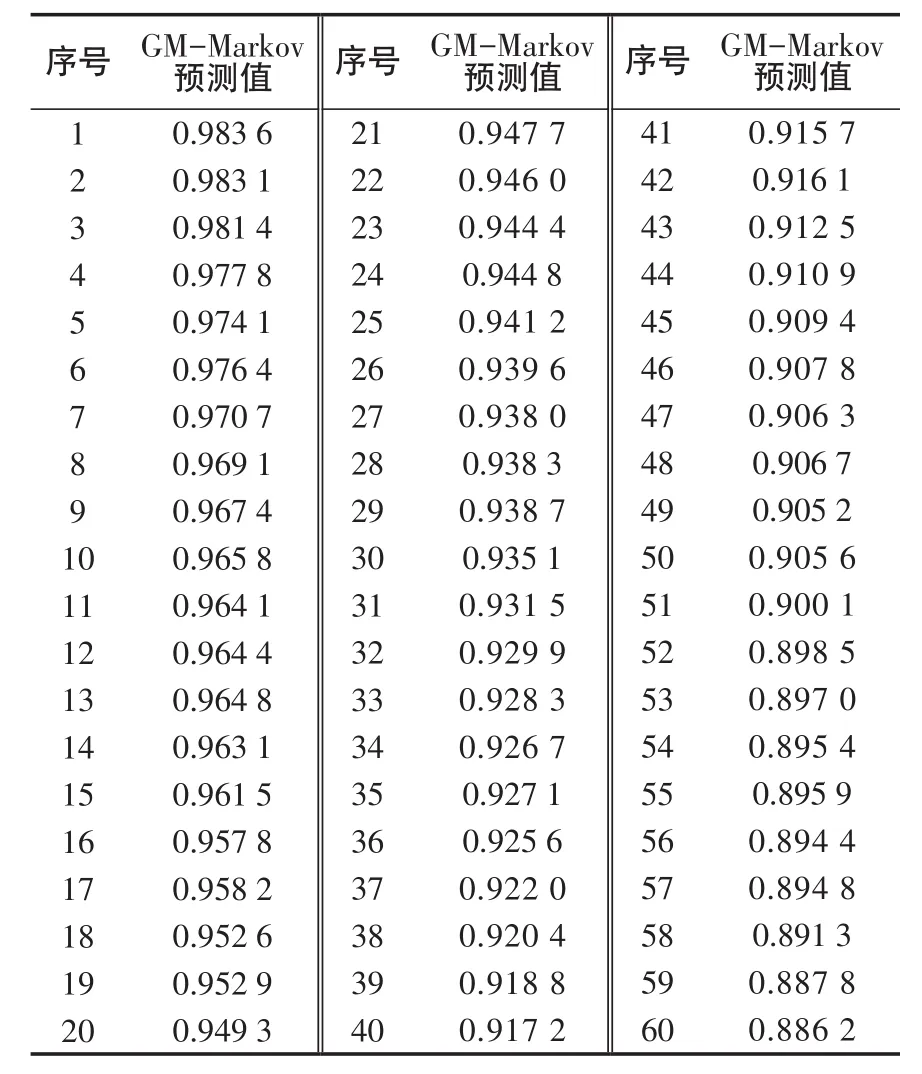
表4 某型导弹贮存可靠度GM-Markov模型预测结果Tab.4 Forecasting result of missile storage reliability with GM-Markov model

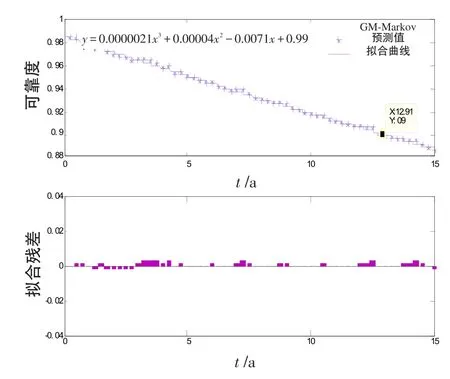
图2 导弹贮存可靠度GM-Markov模型预测值拟合结果Fig.2 Fit result of missile storage reliability with GM-Markov model

4 结束语

本文给出某型导弹寿命评估的灰色—马尔可夫组合预测方法，算例表明所建立的组合预测模型与单一的预测模型相比，结合了灰色预测和马尔可夫预测分别在趋势性和整体波动规律性预测方面的优势，具有更高的预测精度，满足预测的精度要求。该方法能够为准确合理地制定导弹的维修、保养计划提供科学的理论参考。

[1]GERALD A COLLINGWOOD.Solid rocket motor service life prediction using nonlinear viscoelastic analysis and probability approach，AD-A330303[R].1998.

[2]梁旭，李行善，张磊，等.支持视情维修的故障预测技术研究[J].测控技术，2006，26（6）：5-8. LIANG XU，LI XINGSHAN，ZHANG LEI，et al.Survey of fault prognostics supporting condition based maintenance[J].Measurement&Control Technology，2006，26（6）：5-8.（in Chinese）

[3]谢庆华，张琦，卢涌，等.航空发动机单部件视情维修优化决策[J].解放军理工大学学报：自然科学版，2005，6（6）：75-78. XIE QINGHUA，ZHANG QI，LU YONG，et al.Optimizing on-condition maintenance decision-making of aeroengine single parts[J].Journal of PLA University of Science and Technology：Natural Science Edition，2005，6（6）：75-78.（in Chinese）

[4]郝英，孙健国，白杰.航空燃气涡轮发动机气路故障诊断现状与展望[J].航空动力学报，2003，18（6）：753-759. HAO YING，SUN JIANGUO，BAI JIE.State-of-the-art and prospect of aircraft engine fault diagnosis using gas path parameters[J].Journal of Aerospace Power，2003，18（6）：753-759.（in Chinese）

[5]赵鉴，梁志君.从F-35项目来看PHM的应用与效益[J].价值工程，2012（6）：298. ZHAO JIAN，LIANG ZHIJUN.The PHM application and efficiency from the items F-35[J].Value Engineering，2012（6）：298.（in Chinese）

[6]陈海建，滕克难，李波，等.神经网络在导弹贮存可靠性预测中的应用[J].弹箭与制导学报，2010，30（6）：78-80. CHEN HAIJIAN，TENG KENAN，LI BO，et al.Application of neural network on missile storage reliability forecasting[J].Journal of Projectiles，Rockets，Missiles and Guidance，2010，30（6）：78-80.（in Chinese）

[7]郑波，葛广平.基于步进应力加速寿命试验的引信贮存寿命评估[J].北京理工大学学报，2003，23（5）：545-547. ZHENG BO，GE GUANGPING.Estimation of fuze storage life based on stepped stress accelerated life testing[J]. Journal of Beijing Institute of Technology，2003，23（5）：545-547.（in Chinese）

[8]高宏力，李登万，许明恒.基于人工智能的丝杠寿命预测技术[J].西南交通大学学报，2010，45（5）：685-691. GAO HONGLI，LI DENGWAN，XU MINGHENG.Intelligent monitoring system for screw life evaluation[J]. Journal of Southwest Jiaotong University，2010，45（5）：685-691.（in Chinese）

[9]吴进煌，戴邵武，徐胜红.基于可靠度预测模型的导弹贮存寿命分析方法[J].海军航空工程学院学报，2005，20（4）：477-479. WU JINHUANG，DAI SHAOWU，XU SHENGHONG. Analysis method of missile storage life based on forecasting model of storage reliability[J].Journal of Naval Aeronautical and Astronautical University，2005，20（4）：477-479.（in Chinese）

[10]BAGDONAVICIUS V，BIKELIS A.Estimation reliability using failure-degradation data with explanatory variables[J].Journal of Mathematical Sciences，2009，163（3）：202-212.

[11]WEN KUNLI，HUANG YIFUNG，YOU MEILI，et al. The development of GM（1，1）error toolbox[C]//IEEE International Conference on Intelligent and Advanced Systems.2007：276-279.

[12]DENG J L.Control problems of grey systems[J].Systems &Control Letters，1982，1（5）：288-294.

[13]张诚，张广胜.基于优化灰色—马尔可夫链模型的铁路货运量预测[J].技术与方法，2011，30（7）：129-131. ZHANG CHENG，ZHANG GUANGSHENG.Railway freight volume prediction based on optimized GM（1，1）-Markov chain[J].Logistics Technology，2011，30（7）：129-131.（in Chinese）

Evaluation Method of Certain Missile Storage Life Based on Combination Forecasting Modell

XU Ting-xue,XI Wen-jun,ZHAO Jian-yin,ZHAO Liang

（Department of Ordnance Science and Technology,NAAU,Yantai Shandong 264001,China）

It is very important to scientifically determine the storage life of a missile for developing support ability and combat power of army.Then,the combination forecasting modeling method was focused on describeing with less data modeling features gray GM(1,1)forecasting model and suitable for large random fluctuations Markov model.Finally,this model was used to solve the problem of certain missile storage life evaluation.Through the analytic results,the method was better than the single forecasting method,and was regarded of feasibility and high practice value.

GM-Markov;combination forecasting model;missile storage life evaluation

TP301.6

A

2014-01-13；

2014-03-25

国家部委技术基础基金资助项目（1145213）

徐廷学（1962-），男，教授，博导，博士。

1673-1522（2014）03-0230-05

10.7682/j.issn.1673-1522.2014.03.007