小波包能量谱-稀疏核主元在故障检测中的应用

朱丹，范玉刚，邹金慧，吴建德，黄国勇

1.昆明理工大学信息工程与自动化学院，昆明 650500

2.云南省矿物管道输送工程技术研究中心，昆明 650500

小波包能量谱-稀疏核主元在故障检测中的应用

朱丹1，2，范玉刚1，2，邹金慧1，2，吴建德1，2，黄国勇1，2

1.昆明理工大学信息工程与自动化学院，昆明 650500

2.云南省矿物管道输送工程技术研究中心，昆明 650500

针对滚动轴承故障检测的问题，提出一种基于小波包能量谱-稀疏核主元的滚动轴承故障检测方法。对振动信号进行小波包分解，提取信号的能量频谱，用增量式样本基构造方法，提取能量频谱的样本基，以此样本基建立核主元模型，来分析轴承振动信号能量频谱的变化。通过实验仿真来说明此算法的有效性。

滚动轴承；小波包；稀疏核主元；故障检测

1 引言

滚动轴承广泛应用于各种机械设备，其运行状态对整台机器的安全运行影响极大，一旦滚动轴承发生故障或者失效，将对机器运行带来安全隐患。因此，对滚动轴承进行监测、诊断具有重要意义。滚动轴承在不同的工况下运行，产生不同的振动信号，因此可以通过采集滚动轴承工作时的振动信号，并对该信号进行分析和研究，来诊断滚动轴承的运行状况。对振动信号进行小波包分解，得到反映信号特征的频带能量谱。当滚动轴承开始发生故障时，信号的各频带能量中包含了相应的故障信息，即振动信号各频带的能量比例会发生变化，因而可利用滚动轴承振动信号各频段的能量比例来分析轴承的运行情况，以此作为故障诊断的依据。在对滚动轴承进行监测和诊断的过程中，故障信号的分析处理是其中的核心内容，它在提高诊断的准确性和可靠性方面处于非常重要的位置。本文首先对振动信号提取能量频谱，并建立能量频谱的样本基，以此样本基建立多元统计模型，用于分析轴承振动信号能量频谱的变化。

对得到反映信号特征的频带能量谱进行分析，是故障检测的重要内容。主元分析法（PCA）是一种基于多元统计的故障检测方法。然而在现代工业系统中都存在着非线性问题，因此各种非线性PCA方法相继被提出，例如，核主元分析方法（KPCA）[1]。KPCA是一种非线性特征提取方法，得到了广泛的应用[2-5]。然而，核主元分析存在不适合大样本分析、计算复杂的缺点，因此本文提出一种稀疏核主元故障检测方法，对振动信号的小波包能量谱进行分析。首先，将滚动轴承振动信号进行小波包分解，计算各子频带信号的能量值，并构建能量频谱特征向量；其次，对得到的特征向量采用增量式样本基构造方法提取样本基，以此样本基建立正常的核主元模型，用于轴承振动信号故障检测；最后，通过仿真分析，说明了此算法的有效性。

2 小波包的能量谱特征量提取

2.1 小波包分解

小波包分解是在多分辨分解的基础上将各尺度下的细节分量作进一步分解，从而实现对随尺度变小而变宽的频率窗口再划分，提高信号高频部分频率的分辨率，使故障特征提取能够在更加细化的频带内进行。

其中，t=1，2，…，N/2i（N为原始信号的采集点数）；i= 2j，j=1，2，…，J（J为最大分解层数），原始信号经过j层小波分解得到2j个小波包，每个小波包的采样点数为N/2j。

在滚动轴承故障诊断中，将采集到的信号进行小波包分解后，得到2j（j表示分解层数）个分解向量，它们包含着各个频段的信息，而故障信息包含在其中的某些频段内。

2.2 能量谱特征量提取

按照能量方式表示的小波包分解结果称为小波包能量谱，在小波包能量谱中，可以选取各频带内信号的平方和作为能量的标志，为进一步的故障识别提供了诊断的前提条件。以3层小波包分解为例，说明滚动轴承故障信号小波包能量谱特征量提取方法[8-9]：

（1）首先对滚动轴承振动信号进行3层小波包的能量谱特征量提取。

（4）构造轴承故障信号的特征向量。由于系统出现故障时会对各频带内信号能量有较大的影响，因此，以能量为元素可以构造一个特征向量。

（5）特征向量T构造如下：

3 核主元分析

KPCA的基本思想是首先通过非线性映射将原输入空间映射到一个高维的特征空间，然后在高维的特征空间上进行主元分析，从而把输入空间中的非线性问题转化为特征空间中的线性问题。

KPCA是一种非线性方法[10-12]，它首先通过非线性映射φ将原输入空间（x1，x2，…，xN∈Rm)（其中N为采样样本的数目，m为测量变量的维数）映射到一个高维的特征空间F中（即：φ:Rm→F），然后在这个高维的特征空间F内，进行主元分析，从而把输入空间中的非线性问题转化为特征空间中的线性问题。把xi的映射记为φ(xi)=φi，则特征空间F的协方差矩阵可以表示为：

设矩阵CF所对应的特征值为λ，特征向量为v，则存在系数αi(i=1，2，…，N)，使得矩阵CF的特征向量v可以用φi表示为：

在特征空间F上进行主元分析之前，应先作标准化处理，即用下式代替矩阵K：

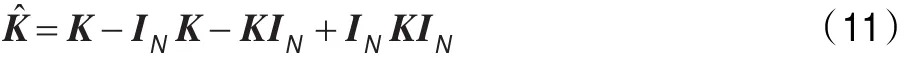
其中，IN等于1/N与一个N×N的单位矩阵E∈RN×N相乘。所以，在特征空间中进行主元分析，就等价于对式（10）求解特征值问题。结合式（10）和式（6），由矩阵K的特征向量α可以求出矩阵CF的特征向量v，且满足：

其中p为主元个数。这样，可以通过计算映射数据在特征向量vk上的投影来计算主元，即

为了解决式（10）的特征值问题，并利用式（13）直接从输入空间计算特征空间的主元向量，在特征空间中引入点积形式的核函数k(x，y)=φ(x)，φ(y)，避免直接计算非线性映射。核函数的选择完全决定映射φ和特征空间F，常用的核函数有：高斯核函数（也叫径向基核函数）：k(x，y)=exp(-‖x-y‖2/σ)；多项式核函数：k(x，y)= x，yd；符号核函数：k(x，y)=tanh(β0x，y+β1)。其中，σ，d，β0和β1需提前指定。

然而，对于那些大型的、复杂的工业过程来说，样本数据一般会很多，这就导致核矩阵的计算复杂，因此KPCA不适合大样本分析。针对这一不足，本文提出稀疏核主元的故障检测方法。

4 基于小波包能量谱的稀疏核主元分析

基于小波包能量谱的稀疏核主元分析方法，将信号各频率段的能量值构造特征向量T，并提取T的样本基，以此样本基建立核主元分析模型。因此，该算法主要包括样本基提取、KPCA模型建立两大部分。

4.1 样本基提取

样本基是稀疏核主元算法的基础，样本基的构造实质是从输入样本集X中找到一个样本子集，满足条件：（1）由该样本子集映射到特征空间的核矩阵满秩；（2）该样本子集是满足条件（1）的最大样本集。

该定理的用途是：当Kn降秩时，第n个样本对应的核变换可用前n-1个样本的核变换线性表示。

由此得到如下的样本基构造算法：

（1）令初始样本基仅包含任意一个样本，d=1，计算相应的核矩阵。

（2）逐个检验样本，计算δ，如果δ=0，则该样本不加入样本基S；否则将加入样本S，并用递推算法修改相应的核矩阵和核矩阵的逆，令d=d+1。

（3）算法结束并得到d和样本基S={s1，s2，…，sd}。

（4）以此样本基取代全部训练样本，建立KPCA模型，称为稀疏核主元。

4.2 基于小波包能量谱的稀疏核主元故障检测

基于小波包能量谱的稀疏核主元故障检测步骤如下：

（1）首先对滚动轴承振动信号进行3层小波包分解，分解算法如式（1），得到第3层从低频到高频的8个频带成分。

（2）求各子频带信号的能量值，计算方法如式（3）。

（3）对能量频谱构成的特征向量T，采用增量式样本基的构造方法构造样本基，以此样本基作为训练样本，建立正常的核主元模型。

（4）将轴承振动信号（本文选取轴承滚动铁和内圈这两种故障）重复步骤（1）、（2），得到振动信号分解后各频段的能量值，以此作为测试样本。

（5）对测试样本进行核主元分析，求取T2和SPE统计量进行故障检测。

5 仿真实验研究

本文采用来自美国西储大学（Case Western Reserve）滚动轴承实验中心的实验数据作为故障检测的依据，从中选取的数据是6205-2RSJEMSKF型的滚动轴承数据，实验装置和轴承尺寸见http：//www.eecs.cwru.edu/laboratory/bearing/。其加速度传感器安装在电机驱动端，空载转速为1 797 r/min（也就是转频为1 797/60 r/s= 29.95 Hz），采样频率为48 kHz，模拟轴承滚动铁和内圈正常与故障的[故障直径为0.014 inch（0.035 56 cm）]振动信号。利用小波包能量谱变化的主元分析方法、标准核主元分析方法和稀疏核主元分析方法，分别对轴承数据进行仿真分析，并比较所得结果，最终验证了稀疏核主元分析方法的有效性。

5.1 频谱分析

选取上面所述条件下的滚动轴承数据，外加一组在此条件下的滚动铁和内圈的故障数据（故障直径为0.007 inch）进行频谱分析，得到的频谱图如图1～图5所示。

图1 正常轴承数据频谱图

图2 滚动铁故障频谱图（故障直径为0.014 inch）

图3 滚动铁故障频谱图（故障直径为0.007 inch）

图4 内圈故障频谱图（故障直径为0.014 inch）

图5 内圈故障频谱图（故障直径为0.007 inch）

由图可看出，正常频谱图大概在0.4×104Hz附近有波峰，而轴承故障频谱图大概在0.3×104Hz附近有波峰，直接观察故障特征不是很明显，所以提出主元分析方法、核主元方法和稀疏核主元方法进一步对轴承数据进行故障检测。

5.2 主元分析

滚动轴承实验数据故障检测的主要步骤如下：

（1）首先选取轴承滚动铁和内圈正常与故障中的400组实验数据进行三层小波包变换，由于采样频率为48 kHz，故分析范围为0～24 kHz，将每组信号分解成8个频段，各节点频率范围分别为：0～3 kHz，3～6 kHz，6～ 9 kHz，9～12 kHz，12～15 kHz，15～18 kHz，18～21 kHz，21～ 24 kHz。计算各节点的小波系数，并求出其能量值。

（2）分别将其作为输入变量进行主元分析，求取主元变量的T2和SPE统计量[14]，检测故障是否发生，如图6～图9所示。

图6 滚动铁故障的T2统计量故障检测图（PCA）

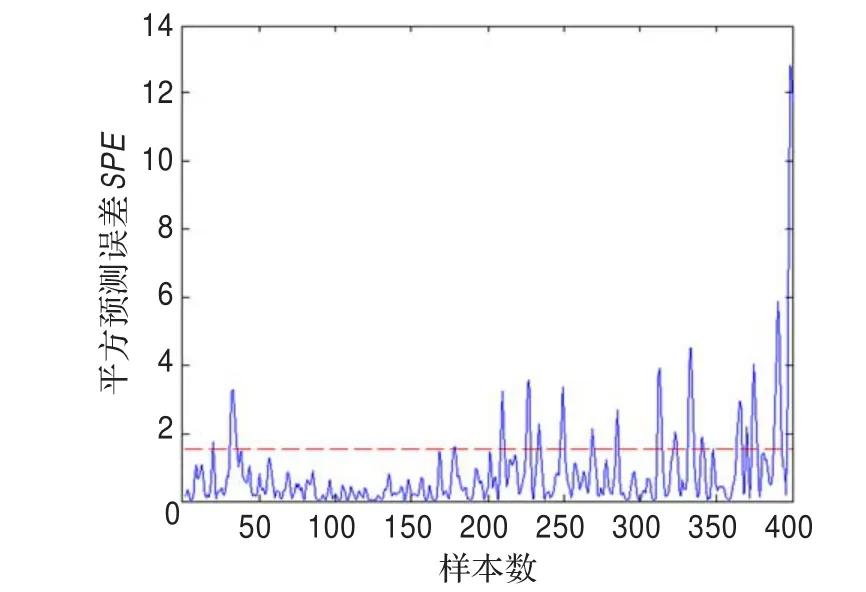
图7 滚动铁故障的SPE统计量故障检测图（PCA）

图8 内圈故障的T2统计量故障检测图（PCA）

本文采用的小波包是db3（Daubechies）正交小波包，经3层小波包分解后，求取各组样本中各频带的频谱能量值。

图9 内圈故障的SPE统计量故障检测图（PCA）

由图6～图9可看出，数据在中间段以后有变化，但变化不是很明显，检测效果不好，因此提出下面的稀疏核主元故障检测方法。

5.3 稀疏核主元分析

滚动轴承故障检测步骤同上，核函数选用普遍应用的高斯核，即k(x，y)=exp(-‖x-y‖2/σ)，这里取σ=35。

经3层小波包分解后，求取各组样本中各频带的频谱能量值。先将轴承正常400组数据训练，求得轴承运行的核主元模型，故障控制限为95%。最后分别将滚动铁故障和内圈故障400组测试数据处理后输入核主元模型，求取T2和SPE统计量，如图10～图13所示。

利用4.1节的方法得d=31及相应的样本基S。95%控制限对应滚动铁故障、内圈故障的统计量为T2(95%)= 7.403 7，SPE(95%)=0.247 9，结果见图14～图17。

图10 滚动铁故障的T2统计量故障检测图（标准KPCA）

图11 滚动铁故障的SPE统计量故障检测图（标准KPCA）

图12 内圈故障的T2统计量故障检测图（标准KPCA）

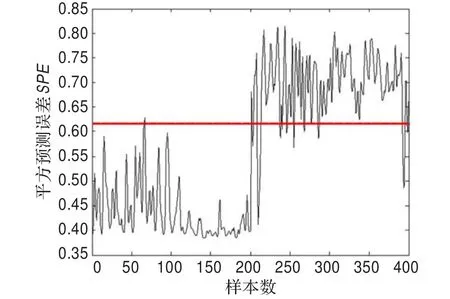
图13 内圈故障的SPE统计量故障检测图（标准KPCA）

图14 滚动铁故障的T2统计量故障检测图（稀疏KPCA）

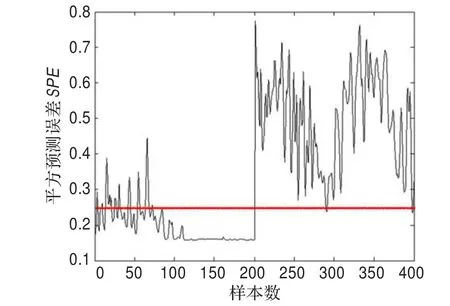
图15 滚动铁故障的SPE统计量故障检测图（稀疏KPCA）

图16 内圈故障的T2统计量故障检测图（稀疏KPCA）

由图10～图17可看出，数据在中间段以后有明显变化，超过限值并持续，可以认为是轴承发生故障，应该予以报警。但在图14～图17（稀疏核主元的T2和SPE统计量故障检测）中，样本数200以后超过限值部分明显，检测出故障信号。从400个测试样本中提取31个样本构成样本基，因此核矩阵从400×400变为31×31，极大减少了KPCA的计算量。与标准KPCA相比，计算效率得到提高，验证了稀疏核主元分析方法在滚动轴承故障检测中的有效性。

6 结论

本文提出的基于小波包能量谱-稀疏核主元的滚动轴承故障检测方法，首先将正常振动信号进行小波包分解，建立能量频谱，并对能量频谱构建特征向量T，对特征向量T采用增量式样本基构造方法提取样本基，以此样本基作为训练样本，建立正常KPCA模型；其次，将轴承信号进行核主元分析，求取T2和SPE统计量，进行故障检测。稀疏核主元方法基于样本基，从而提高了计算效率。理论分析和实验结果表明，利用该方法进行滚动轴承的故障检测是有效的。

图17 内圈故障的SPE统计量故障检测图（稀疏KPCA）

[1]Schlkopf B，Smola A，Muller K R.Nonlinear component analysis as a kernel eigenvalue problem[J].Neural Computation，1998，10（5）：1299-1319.

[2]Li Junbao，Gao Huijun.Sparse data-dependent kernel principal component analysis based on least squares support vector machine for feature extraction and recognition[J]. Neural Comput&Applic，2012，21：1971-1980.

[3]Zhang Yingwei，Li Shuai，Hu Zhiyong.Improved multiscale kernel principal component analysis and its application for fault detection[J].Chemical Engineering Research and Design，2012，90：1271-1280.

[4]Nguyen V H，Golinval J C.Fault detection based on Kernel Principal Component Analysis[J].Engineering Structures，2010，32：3683-3691.

[5]赵小强，王新明，王迎.基于PCA与KPCA的TE过程故障检测应用研究[J].自动化仪表，2011，32（1）：8-12.

[6]张亿雄，顾海明，周勇军.小波包分析在滚动轴承故障诊断中的应用[J].煤矿机械，2009，10（30）：240-242.

[7]孙洁娣，靳世久.基于小波包能量及高阶谱的特征提取方法[J].天津大学学报，2010，43（6）：563-566.

[8]王冬云，张文志.小波包能量谱在滚动轴承故障诊断中的应用[J].测量与仪器，2010（11）：32-36.

[9]姜娜，纪建伟.基于小波包分析的滚动轴承的故障诊断方法研究[J].浙江农业学报，2012，24（2）：310-313.

[10]Xiao Yingqun，Feng Lianggui.A novel neural-network approach of analog fault diagnosis based on kernel discriminant analysis and partical swarm optimization[J].App-Lied Soft Computing，2012，12：904-920.

[11]彭涛，杨慧斌，李健宝，等.基于核主元分析的滚动轴承故障混合域特征提取方法[J].中南大学学报，2011，42（11）：3385-3391.

[12]Jin Xiangyang，Lin Lin，Zhong Shisheng，et al.Rotor fault analysis of classification accuracy optimization based on kernel principal component analysis and SVM[J].Procedia Engineering，2011，15：5279-5283.

[13]付克昌，吴铁军.基于特征子空间的KPCA及其在故障检测与诊断中的应用[J].化工学报，2006，57（17）：2265-2269.

[14]许丽，张进明.基于PCA的滚动轴承故障检测方法[J].计算机仿真，2010，27（6）：325-329.

ZHU Dan1，2,FAN Yugang1，2,ZOU Jinhui1，2,WU Jiande1，2,HUANG Guoyong1，2

1.Faculty of Information Engineering andAutomation,Kunming University of Science and Technology,Kunming 650500,China
2.Engineering Research Center for Mineral Pipeline Transportation,Kunming 650500,China

For the problem of rolling bearing fault detection,a method of rolling bearing fault detection is proposed,which is based on wavelet packet energy spectrum and sparse kernel principal component.The vibration signal is decomposed by wavelet packet,in order to extract the energy spectrum of the signal.Then the sample base of energy spectrum is extracted through the method of incremental sample base.A kernel principal component model is built by the sample base for the analysis of the energy spectrum of the bearing vibration signal.The experimental simulation is presented to illustrate the effectiveness of the algorithm.

rolling bearing;wavelet packet;sparse kernel principal component;fault detection

A

TP277

10.3778/j.issn.1002-8331.1301-0027

ZHU Dan,FAN Yugang,ZOU Jinhui,et al.Application of wavelet packet energy spectrum and sparse kernel principal component in fault detection.Computer Engineering and Applications,2014,50（21）：224-229.

国家自然科学基金（No.51169007）；云南省科技计划项目（No.2010DH004，No.2011DA005，No.2012CA022）；云南省中青年学术和技术带头人后备人才培养计划项目（No.2011CI017）。

朱丹（1987—），女，硕士，研究领域为基于声发射的故障检测；范玉刚（1973—），通讯作者，男，博士，副教授，研究领域为基于机器学习的智能信息处理、数据挖掘技术等；邹金慧，女，副教授；吴建德，男，博士，教授；黄国勇，男，博士，副教授。E-mail：406742487@qq.com

2013-01-06

2013-04-17

1002-8331（2014）21-0224-06

CNKI出版日期：2013-04-26，http://www.cnki.net/kcms/detail/11.2127.TP.20130426.1018.001.html