遗传算法的阶梯电价用电需求管理方案

杨曦华，胡晓敏

1.中山大学信息科学与技术学院，广州 510006

2.中山大学公共卫生学院，广州 510080

遗传算法的阶梯电价用电需求管理方案

杨曦华1，胡晓敏2

1.中山大学信息科学与技术学院，广州 510006

2.中山大学公共卫生学院，广州 510080

用电需求管理是智能电网中的重要部分，能让消费者根据自己的用电量做出合适的决策，帮助供电者减少峰值负载，让负载的时空分布更为均衡，从而增加智能电网的可持续性，并减少运营成本和碳排放量。一种基于负载转移技术的用电需求管理方案可以满足对大量、多种设备的调节需求。用电需求管理的解决方案使用改进的遗传算法，并引入了一个新的算子，模拟测试的结果显示通过改进的算法获得的方案节省了可观的成本，并且在使用阶梯式电价的情况下，减少了智能电网的峰值负载。

智能电网；遗传算法；阶梯电价；用电需求管理；负载转移

1 引言

根据美国能源部的定义，智能电网[1-2]是一个完全自动化的电力传输网络，能够监视和控制每个用户和电网节点，保证从电厂到终端用户整个输配电过程中所有节点之间的信息和电能的双向流动，建立在先进的传感技术、控制技术、通信技术以及决策系统的应用之上。其主要特征[2]包括消费者友好、安全性能高、能兼容各种发电形式、高效地保持电力市场的运作、保证高质量的电力供给、获取最大经济效益等。这种现代电网是在经济、政治、环境、社会和科技等多种因素的共同作用下出现的。用电需求管理[3-4]是未来智能电网的电力管理中的重要部分，能够保证智能电网在多个区域中运作。合理地管理电力需求可以减少峰值负载，让用电曲线更为平滑，使电网使用具备可持续性，同时降低运营成本和碳排放量。

在用电需求管理中，各种文献[4-16]都提出了多种可供采用的技术和算法，但其中大部分都是只适用于特定系统的方案，另外一些则不能应用于实际的、具有大量不同种类设备的系统。这些方案有许多都是用动态编程[11]、线性编程[5，8]等传统方式来实现的，而它们并不能处理大量的、种类繁多的可控制设备的用电需求。在智能电网中，一个好的调度方案必须能够处理多种的、大量的可控制设备的负载请求，另外还要能够考虑到这些负载有可能在时间上延续多个时段。因此，所求的方案应该具有在其可控时间内不断处理大量可调控负载的能力。一些文献[12-16]则提出了更适合应用于智能电网的算法：文献[12-13]提出了根据市场变化来动态地对用电需求进行调度的负载迁移算法，达到了使每个时刻的负载变化更为平滑的目的。文献[14-16]提出了针对动态变化电价的电价预测算法，运用了小波变换、神经网络、模糊逻辑、支持向量机等工具来对电价进行预测。本文也参考了这些文献中提出的方法，其中文献[12-13]的负载迁移算法使得负载曲线变得更为平滑，但是没有考虑到可能多阶电价的情况，单纯考虑负载平滑可能反而在某些情境下会导致高电价。而文献[14-16]则达到了较为精确地预测电价变化并依此进行决策的目的，考虑到国内主要采用的是固定多阶电价，因此文献[14-16]中的算法并不能完全适应我国国情。

另外，在现代电网逐渐向智能电网转变的过程中，人们又发现了用电需求管理的新特性。首先，在智能电网中发电的一个重要特点是发电来源很有可能来自风能、太阳能等可再生能源[17]，而这些能源的不稳定性会导致智能电网中的电力分配难度较高。其次，智能电网的运营需要在中央控制器和许多系统组件之间进行双向通信，因此相应的用电需求管理系统应该能够处理中央控制器和可控制设备之间的通信。最后，决定最优用电曲线的标准可能十分多样化，有可能包括以最大化地利用可再生能源、获得最大经济效益、最小化从外部主电网输入的电量或减少峰值负载等。

本文提出了一种用于给出可供智能电网使用的用电需求管理方案的算法（Demand Side Management algorithm，下称DSM算法），该算法基于负载转移技术，可以用于处理大量且种类较多的设备的用电请求。应用了遗传算法的思想来解决这一问题[18-21]，并模拟了一个包含不同种类的消费者和大量设备的智能电网来进行测试。同时，对遗传算法的一些算子进行了优化，使其性能相比传统遗传算法有所提高。

DSM算法采用了负载转移的思想，即通过中央控制器对某些请求进行延时，把位于用电高峰的请求尽量向用电低谷转移，可以用于提高可再生能源的利用率、增加经济效益、降低峰值负载等等[22]。根据调控目标的不同，可以根据每天的电价变化曲线、能源利用率曲线等信息计算出一条对应的最优用电量曲线，而DSM算法的目的就是通过对各设备的用电请求进行调度，让实际用电量曲线最可能地向最优用电量曲线靠近。中央控制器要知道一天中每个时刻各类设备的使用数量，得出一个用电请求的序列，对于每一个请求要判断是否接受，若不接受要延后到什么时刻执行，而判断是否接受请求的依据与最优用电曲线有关。这一算法的一个优势就是只需要稍作改动就可以执行不同的目标、应用于不同的系统，具有较好的重用性。

用电需求管理从一个约定好的控制时段的开头开始运行，这个时段一般是一天，对用电请求的调度是实时的。用电设备需要用电时会向中央控制器提出请求，而中央控制器则根据已经计算好的调度方案回复对这个请求的处理结果，处理结果要么立即接受请求，要么给出一个允许下次提出请求的时间。

为了让算法更好地适应实际情况，本文使用的实验数据采用了分两阶的阶梯电价。阶梯电价的基本模式与国内用电政策保持同步，用电量为0～800单位时为基础用电量，电费按照一阶电价计算，超过800单位时，电费按照二阶电价计算。而在一天中的各个时刻，电价保持不变。

2 数学模型

该方案通过将某些用电请求进行延迟以使得实际用电曲线向最优用电曲线靠近，即令

最小化，其中N为时间段的数量，Objective(t)为时刻t的最优用电量，如何判断是否最优与该方案要达到的目标有关，Pload(t)为时刻t的实际用电量。Pload(t)通过下式得出：

其中Unshiftable(t)为该时刻不可调节的固定电量，Connect(t)为在该时刻接受请求的用电设备的总用电量与在该时刻之前接受请求且持续运行到该时刻的用电设备的总用电量之和。Connect(t)通过下式得出：

其中Xkit是请求被从时刻i转移到时刻t的第k种设备的数量，P1k是在第k种设备在开始运作的第1个时间段内的用电量，D是设备数量，j是第k种设备的持续工作时长。

在实际问题中还有一些额外的约束，包括：

对请求的延时必须为非负整数，即调度只能向后延迟，不能把请求向前提前。

3 算法描述

由于实际问题中涉及到大量的设备种类、数量，传统的线性编程和动态编程应用的算法难以处理这样的复杂问题[19]，因此本文采用的是遗传算法，目的是获取相对优良的解决方案[18-19]。问题的规模影响的只是算法中个体的长度，而只要对算法的评价函数作少量修改就可以让该算法针对不同的目标进行运作。在文中以用电费用最小化为算法运行目标。

3.1 编码方案

算法中个体的基因数量L=N×K，其中N为时间段的数量，K为设备类型总数。每位基因表示对该时刻该种设备提出请求的处理情况，为一个形式如a1，s1，a2，s2…的数列，其中ai和si表示该时刻该种设备的请求中，有ai个请求需要延后si个时间段才能被接受。

3.2 适应性评价

在实际问题中，电价是分阶段收费的，用电量较少的用户平均单位电费也较低，从而达到促进节约用电的目的。在本文算法中同样引入了这种模型，若Stagei≤Pload(t)＜Stagei+1，则代表该时刻的用电量对应第i阶电价。对适应值的评价函数如下：

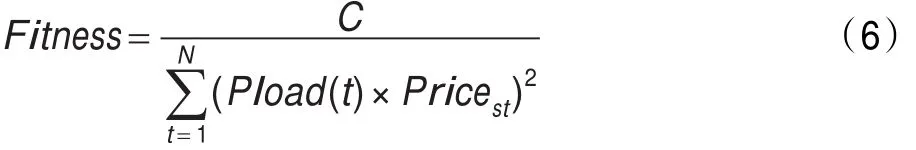
其中C是一个用于调整适应值区间的常数，Pricest表示在时刻t，该区域的用电量对应的第s阶电价。

3.3 遗传算子

遗传算法从已有的种群中不断择优产生新种群，本文提出的算法中用到的算子包括两点杂交、单点变异、扭转。较高的杂交率会让解较快收敛，而过高的变异率则会让优秀的个体难以出现和保持。通过测试，可以根据不同的问题分别找到最优的杂交率和变异率（本文采用0.7和0.02作为杂交率和变异率）。

之所以采用两点杂交而不是单点杂交，是因为两点杂交时交换的个体段的长度较短，能够更好地丰富种群多样性，也避免发生杂交时对种群的影响过大。

在算法运行的后期，变异率过高有可能导致算法的解不稳定，但在前期变异率过低又有可能降低种群多样性，因此在变异算子上乘上了一个随着进化代数呈指数形式减小的常数，让变异率在进化过程中随着进化代数增加而逐渐减小，同时解决了两方面的问题。

与原算法相比，提出了借鉴生物界中近亲杂交的扭转算子。近亲杂交的特点是交配双方的基因比较相似，因此相比远缘杂交而言会同时提高致病基因和优良基因的出现概率。在遗传算法中，可能难以判断单个基因是致病基因还是优势基因，但是可以将个体和该问题理论上的最优个体进行比较。在微电网电力调度问题中评价函数的函数值不会因为基因的微小变动而出现大幅度的波动，从而在这一背景下，两个个体的基因越接近，它们的适应值相近的概率也就越大。

因此，扭转算子被用来以某个个体为蓝本，快速复制出一些与该个体基因相近的近亲个体。当蓝本个体本身就是一个优势个体时，如果在这些近亲个体之间应用杂交算子，虽然会产生许多劣势个体，但是同时与原种群相比也提高了优势个体的出现概率；即使在某些情况下该算子可能产生较大的破坏性，也可以通过调整触发概率的方式来解决这个问题。

同时这个算子还有另一个应用，如果当算法的进化代数远未达到最大代数时，适应值的增长就已经开始长时间停滞，就有理由认为该算法有可能收敛到了一个次优解。此时可以保存当前最优的若干个体，并以其为蓝本制造出若干近亲个体，替换掉原种群中的一部分个体，再让算法继续运行。这实际上是让算法进行了部分的回滚，但在回滚过程中并未完全浪费之前的进化过程，而是保留了其中有可能代表优秀性状的部分基因。扭转算子的工作原理并不复杂，让蓝本个体的每个基因与一个微小的随机实数相加，就得到了一个近亲个体。

3.4 选择

选择算法采用的是锦标赛与轮盘赌的结合。但单纯使用这两种方法容易引发结果收敛过快，因此在选择过程中先从亲代种群中用轮盘赌选择一部分个体复制到新种群中，然后再通过锦标赛、轮盘赌等方式选出足够数量的各不相同的个体加入新种群。这种方式可以避免因超级个体导致的多样性丧失。当种群进化了一定代数（如5 000代）时，算法终止。DSM算法流程图如图1所示。

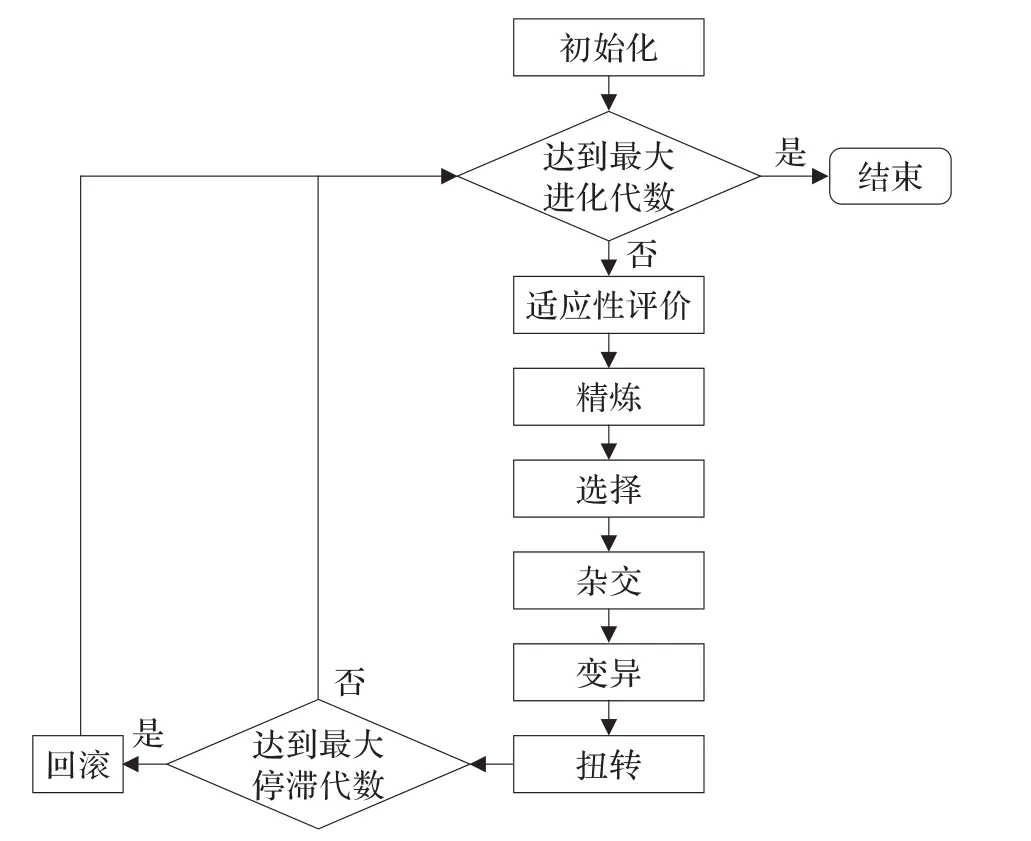
图1 DSM算法流程图

4 实验设置

为了便于比较，本文使用的测试实例数据来自文献[17]，包括商业区和居住区两种用电区域，对于每个区域内部都需要计算出一个最优调度方案。因为各个区域之间、该电网和外部电网之间都可以互相传输电力，因此测试时假定提出的用电请求一定可以被满足。测试中算法的运行目标是使消费者支付的电费最少。

表1给出了用电价格和24 h内的预测用电量。居民区和商业区两种区域的区别在于居民区的用电设备种类最多，包括14种共2 604个可控设备，商业区中有8种共808个可控设备，设备的运作持续时间较居民区的时间长。商业区每种设备的运作时间和每小时的耗电量见表2，居住区情况见表3。在本文采用的测试用例中，电价分级，用电量在800单位以下时按一阶电价计算，超过800单位的部分按二阶电价计算，因此理想的调度方案应当使得一天中大部分时间的用电量维持在800单位以下。

表1 用电价格和预测用电量

表2 商业区设备工作时间和用电量

下面将分析各区域的测试情况以及电价曲线，检验电价阶数为2时DSM算法的性能表现，并与传统遗传算法进行性能对比。此处传统遗传算法是指去除了DSM算法中的扭转算子和回滚函数的算法，其他算子、函数、参数和测试数据保持不变。

表3 居住区设备工作时间和用电量

在测试时，对每个区域都使用了10个样例进行测试，样例之间的差别主要在于用电器提出请求的顺序、时间和数量，而电价、用电器总量、一天的总用电量都是相同的。对于每个样例都独立进行20次测试，由于在几次测试之间可以记录最优个体的基因用作扭转算子的蓝本，因此随着测试次数增多会对结果有一定的改进，这里取最优结果作图。图2和图3中的初始用电量曲线代表由设备用电请求直接构成的初始方案对应的用电量曲线。

图2 商业区初始预测用电量曲线

图3 居住区初始用电量曲线

5 结果分析

从图2和图3可以看出在10个样例中，初始的可调节用电量的分布很随机。由于初始每个时刻的用电量已知，在初始可调节用电量确定的前提下，每个时的固定用电量就可以得出。采用算法调度可调节设备的用电量，使每个时刻的用电量尽量控制在800单位以下，才能尽可能减少电费的开支。

图4 两种算法对商业区的计算结果对比图

图4和图5给出了采用本文提出的DSM算法与使用传统的GA算法对商业区和居住区测试实例的优化曲线图。可以看出，在两个区域的大部分样例的进化过程中，DSM算法的收敛速度均优于传统GA算法，尤其是在算法运行的中前期和停滞期，这使得DSM算法可以更快地获得一个较优的调度方案。

图5 两种算法对居住区的计算结果对比图

表4和表5给出了商业区和居住区采用DSM算法、传统GA算法与对初始方案不进行优化（无优化）下的电费测试平均值。优化率A-B一栏表示的是A算法获得的结果相对B算法获得的结果改善了多少。

表4 商业区测试结果对比

表5 居住区测试结果对比

从表4和表5可以看到对于商业区，DSM算法在用电费用上相对于初始方案都起到了5%以上的优化作用，平均可以达到9%，而对于居住区，平均可以节省23%的费用，对于一个经济问题来说这些节省的电费是相当可观的。而对于传统的GA算法，DSM算法也能得到较优的优化率。

综合上面的图示和表格的结果，首先从两个区域的进化曲线对比图可以看出，应用了扭转算子和回滚函数后，DSM算法在收敛速度上优于传统GA算法，同时也没有因为加快了速度而收敛到局部最优解，而是在大多数测试用例中相比传统GA算法都获得了更好的解。从表4、表5中可以看出应用了扭转算子和回滚函数后，在商业区的10个样例中有6个样例的测试结果优于传统遗传算法所得结果，电费平均减少了0.21%；在居住区的10个样例中有7个样例的测试结果优于传统遗传算法所得结果，电费平均减少了0.04%。这种性能提升看似微不足道，但是对于区域电费这种基数较大的经济活动而言仍然是值得重视的，同时扭转算子和回滚函数对于收敛速度的改善也不容忽视。

下面进一步分析算法对于减少峰值负载的优势。从表6可以看出DSM算法在两个区域的所有样例中都使峰值负载显著地降低了。当然，实际问题中初始方案可能优于测试中使用的初始方案，但只要初始方案并不是最优解，就可以尝试使用DSM算法进行进一步优化。

表6 基于DSM算法优化后商业区和居住区峰值负载

图6 应用DSM算法后得到的商业区总用电量

图6和图7给出了应用DSM算法后得到的商业区和居民区每时刻的用电量曲线图。可以看出，在应用了DSM算法后，算法尽可能地把一天当中相当长时间段的用电量控制在了800单位以下，即满足一阶电价，因此DSM起到了让用电量曲线趋向于目标曲线的目的，而之所以不能完全吻合，主要与最大延长时间的限制和该时段固定电量占总用电量的比例有关。总体来说，模拟测试的结果显示，DSM算法得出的用电需求管理方案大体上完成了让实际用电曲线向最优用电曲线靠拢的目的，使用的算法成功有效地处理了大量、多种设备的用电请求，使智能电网得以良好运营。

图7 应用DSM算法后得到的居住区总用电量

6 结论

在智能电网的运营中，由于涉及到的因素较多、较为复杂，用传统的算法来解决效率相对较低，因此可以使用本文中的DSM算法，对于快速地获得最优或次优的解决方案是很有帮助的。本文的实验结果表明该算法具有较好的收敛性和运行速度，可以较为准确快速地解决智能电网中电力调度的问题。同时，该算法中应用的扭转算子和回滚函数均对算法性能有所提高，这两个机制的缺点是对于不同的问题表现出的性能不够稳定，并不是所有情况下性能都优于传统GA算法，有待在以后的研究中继续改进。

[1]Li Q，Zhou M.The future-oriented grid-smart grid[J].J Comput，2011，6（1）：98-105.

[2]Agrawal P.Overview of DOE microgrid activities[C]//Proc Symp Microgrid，Montreal，QC，Canada，2006.

[3]Rahman S，Rinaldy.An efficient load model for analyzing demand side management impacts[J].IEEE Trans on Power Syst，1993，8（3）：1219-1226.

[4]Cohen A I，Wang C C.An optimization method for load management scheduling[J].IEEE Trans on Power Syst，1988，3（2）：612-618.

[5]Ng K H，Sheblé G B.Direct load control—a profit-based load management using linear programming[J].IEEE Trans on Power Syst，1998，13（2）：688-694.

[6]Schweppe F C，Daryanian B，Tabors R D.Algorithms for a spot price responding residential load controller[J].IEEE Trans on Power Syst，1989，4（2）：507-516.

[7]Lee H，Wilkins C L.A practical approach to appliance load control analysis：a water heater case study[J].IEEE Trans on Power App Syst，1983，PAS-102（4）：1007-1013.

[8]Kurucz C N，Brandt D，Sim S.A linear programming model for reducing system peak through customer load control programs[J].IEEE Trans on Power Syst，1996，11（4）：1817-1824.

[9]Chu W C，Chen B K，Fu C K.Scheduling of direct load control to minimize load reduction for a utility suffering from generation shortage[J].IEEE Trans on Power Syst，1993，8（4）：1525-1530.

[10]Weller H G.Managing the instantaneous load shape impacts caused by the operation of a large-scale direct load control system[J].IEEE Trans on Power Syst，1988，3（1）：197-199.

[11]Hsu Y Y，Su C C.Dispatch of direct load control using dynamic programming[J].IEEE Trans on Power Syst，1991，6（3）：1056-1061.

[12]Deindl M，Block C，Vahidov R，et al.Load shifting agents for automated demand side management in micro energy grids[C]//Second IEEE International Conference on Self-Adaptive and Self-Organizing Systems，2008.

[13]Steen D，Tuan A，Bertling L.Price-based demand-side management for reducing peak demand in electrical distribution systems—with examples from Gothenburg[C]// NORDAC，2012.

[14]Motamedi A，Zareipour H，Rosehart W D.Electricity price and demand forecasting in smart grids[J].IEEE Trans on Smart Grid，2012，3（2）：664-674.

[15]Catalão J P S，Pousinho H M I，Mendes V M F.Shortterm electricity prices forecasting in a competitive market by a hybrid intelligent approach[J].Energy Conversion and Management，2011，52：1061-1065.

[16]Zareipour H，Janjani A，Leung H，et al.Electricity price thresholding and classification[C]//IEEE Power and Energy Society General Meeting，2011.

[17]Logenthiran T，Srinivasan D，Shun T Z.Demand side management in smart grid using heuristic optimization[J]. IEEE Trans on Smart Grid，2012，3（3）：1244-1252.

[18]Yao L，Chang W C，Yen R L.An iterative deepening genetic algorithm for scheduling of direct load control[J]. IEEE Trans on Power Syst，2005，20（3）：1414-1421.

[19]Back T，Fogel D，Michalewicz Z.Handbook of evolutionary computation[M].New York：IOP Publ and Oxford Univ Press，1997.

[20]Hu Xiaomin，Zhang Jun.Hybrid genetic algorithm using a forward encoding scheme for lifetime maximization of wireless sensor networks[J].IEEE Transactions on Evolutionary Computation，2010，14（5）：766-781.

[21]Hu Xiaomin.Multiobjective genetic algorithm for demand side management of smart grid[C]//Proc of the IEEE Symposium Series on Computational Intelligence（SSCI2013），2013：14-21.

[22]Maharjan I K.Demand side management：load management，load profiling，load shifting，residential and industrial consumer，energy audit，reliability，urban，semi-urban and rural setting[M].Saarbrücken，Germany：LAP（Lambert Acad Publ），2010.

YANG Xihua1,HU Xiaomin2

1.School of Information Science and Technology,Sun Yat-sen University,Guangzhou 510006,China
2.School of Public Health,Sun Yat-sen University,Guangzhou 510080,China

Demand side management plays an important role in smart grid business,which allows consumers to choose a suitable electricity consuming strategy according to their demand,lowers the peak load in smart grid,and makes the load curve even.These characteristics lead to a more sustainable,economical smart grid,and a reduction on carbon emission.A demand side management strategy based on a load-shifting technique is proposed,which will be able to manage the demand that comes from large quantities and types of devices.The strategy is carried out with an improved genetic algorithm which imports a new operator.Simulation shows that the resulting strategy generated by the proposed algorithm saves appreciable cost,and reduces the peak load of the smart grid when involving a multistep electricity price.

smart grid;Genetic Algorithm（GA）;multistep electricity price;demand side management;load shifting

A

TP391

10.3778/j.issn.1002-8331.1308-0199

YANG Xihua,HU Xiaomin.Demand side management strategy on multistep electricity price using Genetic Algorithm.Computer Engineering and Applications,2014,50（21）：264-270.

国家自然科学基金（No.61202130）；中央高校基本科研业务费专项资金资助（No.12lgpy47）；高等学校博士学科点专项科研基金资助课题（No.20120171120027）；广东省自然科学基金（No.S2012040007948）。

杨曦华，男，主要研究领域为优化算法、智能计算；胡晓敏（1983—），通讯作者，女，博士，讲师，主要研究领域为计算智能、数据挖掘、建模与优化。E-mail：xmhu@ieee.org

2013-08-15

2013-09-30

1002-8331（2014）21-0264-07

CNKI出版日期：2014-01-15，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1308-0199.html