一种改进的综合生产计划动态规划优化方法

曾强，沈玲，吴立云，兰建义

1.河南理工大学能源科学与工程学院，河南焦作 454000

2.河南理工大学安全科学与工程学院，河南焦作 454000

一种改进的综合生产计划动态规划优化方法

曾强1，沈玲2，吴立云1，兰建义1

1.河南理工大学能源科学与工程学院，河南焦作 454000

2.河南理工大学安全科学与工程学院，河南焦作 454000

提出了一种改进的综合生产计划动态规划优化方法。以1999年甘应爱主编的《运筹学》第227～230页给出的一类综合生产计划问题为研究对象，深入分析了原综合生产计划问题、数学优化模型、动态规划求解过程、计算方法存在的不足并提出了相应的改进措施。通过案例分析验证了所提方法的有效性。

动态规划；综合生产计划；计算机优化

综合生产计划是指导生产的纲领。综合生产计划的优劣决定了生产绩效的高低，研究生产计划优化方法具有重要意义。按优化目标可将综合生产计划优化分为单目标优化[1]和多目标优化[2-3]。按计划对象可将综合生产计划优化分为单一产品综合生产计划优化[4]和多产品综合生产计划优化，多产品综合生产计划优化更为复杂。按是否考虑能力约束可分为无限能力约束和有限能力约束下[5]的综合生产计划优化。无限能力约束情况下的综合生产计划可执行性差，常发生计划不能按时完成的情况。按求解方法分为经验法、数学模型法。经验法是凭借计划者的经验进行各期生产量的安排的方法，其计划方案的优劣取决于计划者的经验，不同的计划者做出的计划可能相差较大。数学模型法则是指借助数学优化模型，运用数学优化方法如线性规划法[3，6]、动态规划法[4，7-9]、运输法[4，7]等对数学模型进行求解。按计算方法可分为手工优化和计算机辅助优化两种。手工计算仅适用于计算简单、计算量小的场合，对于计算复杂、计算量大的综合生产计划优化问题，手工计算的时效性差、准确性差，故需借助计算机辅助求解。从以上分析可见，综合生产计划优化是一个复杂的系统优化问题，针对不同的边界条件，能组合出多种不同的优化问题，现实中并不存在普遍适用的解决方案，需根据具体问题进行具体处理。

本文以文献[4]提出的一类综合生产计划优化问题为研究对象，它是一个单目标、单一产品、有限能力约束的多阶段优化决策问题，适合采用动态规划方法对其求解。然而，文献[4]所描述的综合生产计划优化问题在问题假设、数学优化模型、求解过程、计算方法四个方面均存在不足，有必要进行改进。基于此，本文深入分析了文献[4]中原综合生产计划优化问题、数学优化模型、求解过程、计算方法存在的不足并针对这些不足提出了相应的改进措施。

1 原综合生产计划问题改进

文献[4]研究的综合生产计划优化问题描述如下：设某公司对某种产品要制定一项n期的生产计划。已知它的初始库存为0，每期生产该产品的数量有上限，每期市场对该产品的需求量已知，公司保证各期的供应（不允许缺货），在第n期的终结库存为0，问该公司如何制定各期的生产计划，使总成本最低。

由上述问题描述可以看出，原生产计划问题存在如下不足：（1）假设期初和期末库存为0，大大限制了应用范围。实际生产实践中，由于存在瓶颈期和生产能力的共同制约，很有可能需要在期初保有一定的库存以满足瓶颈期的需求，故期初库存可能大于0。同样的道理，为满足下一计划期中的瓶颈期的需求，需要在上一计划期多安排生产使期末库存大于0，上一计划期的期末库存也就成为下一计划期的期初库存。（2）假设各期生产能力上限相同，也与生产实际不一定相符。实际生产实践中，由于受计划期中各期人力、设备、工具、工作日历及管理等因素波动的影响，各期的生产能力上限不一定相等。基于以上分析，本文提出如下的改进措施：将约束条件放宽，即假设期初库存大于等于0、期末库存大于等于0，各期生产能力上限可不同。

2 综合生产计划数学优化模型改进

（1）变量及函数定义

n为计划期的总期数；k为第k期，k∈[0,n]；Dk为第k期需求量；Xk为第k期生产量；Vk为第k期期末库存；Ck(Xk)为第k期生产量为Xk时的生产成本；Hk(Vk)为第k期期末库存为Vk时发生的存贮成本；m为生产能力上限。

（2）原生产计划数学优化模型

根据问题描述及变量定义，可得到如式（1）（2）表示的数学优化模型。

（3）改进后生产计划数学优化模型

根据对生产计划问题的改进措施，新定义变量Uk为各期生产能力上限，对上述数学优化模型进行了改进得到如式（3）（4）表示的数学优化模型。

3 动态规划求解过程改进

若对式（1）（2）数学优化模型采用动态规划方法来求解，其状态转移方程和顺序递推关系如式（5）、（6）所示。

4 综合生产计划动态规划计算机求解方法

由文献[4]对原问题的计算过程可以看出，其计算量很大，随着计划期、需求量、生产能力的增加，计算量将呈指数式增长，使得手工计算时效性差，并且手工计算具有出错率高的特点，因此它无法适应复杂的动态规划问题的求解。基于此，本文针对改进后的一类综合生产计划优化问题、数学优化模型及动态规划求解过程的特点，研究并提出一种计算机辅助求解方法。下面对该方法进行简要阐述。

表1 变量定义

4.1 变量定义

为便于计算机编程和后续内容的描述，对所用到的变量说明如表1所示。

4.2 工作表设计

为便于利用Excel求解，需根据动态规划问题的特点将相关数据映射成Excel工作表。程序计算过程中有关数据的输入、中间计算结果、输出均通过工作表进行。各表之间可能存在相互关联的关系，如“计算过程”与“计算结果”之间彼此关联，这通过各单元格的公式实现联动，而这些公式的输入则通过程序写入。根据所研究问题的特点，主要设计了四张工作表，即“生产需求及能力约束”、“计算过程”、“计算结果”、“最优方案”。其中，“生产需求及能力约束”用于输入各期需求量及生产能力上限，其结构如表2所示；“计算过程”用于存储整个计算的中间过程数据，以便追踪计算的全部过程，其结构如表3所示；“计算结果”用于存储最终计算的生产计划方案，其结构如表4所示。“最优方案”工作表结构与“计算结果”的结构完全相同，所不同的是它仅存储系统输出的最优方案，是计算结果中的一部分内容。

表2 生产需求及能力约束

表3 计算过程

表4 计算结果

4.3 计算流程

本文提出的综合生产计划动态规划计算机求解方法总体思路如下：首先通过程序自动填充计算公式于“计算过程”和“计算结果”两个工作表，然后根据用户设置的期末目标库存量自动输出该期末库存量下对应的最优生产计划。

自动填充“计算过程”和“计算结果”两个工作表通过三层嵌套循环来实现。第一层（最外层）令k从1到n变化；第二层（中间层）令Vk从0到Vkmax变化；第三层（最内层）令Xk从0到Sgmk变化。通过三层循环，将k、Vk、Xk的每种组合在“计算过程”工作表中以公式的形式在各单元格中输出；同时，对于每个k，当进行了第二层和第三层循环之后，将最小Fk_Vk值对应的行输出到“计算结果”中以备第k+1期查寻Fk_Vk值时使用。

输出最优方案采用“反向追踪技术”实现，即通过用户设置的最终库存量Vn，在“计算结果”工作表中第n期对应的行中找到Vk列等于Vn值的行，从Vk-1列得到Vn_1值，并将此行输出到“最优方案”的n+2行，然后在第n-1期中寻找Vk列的值等于Vn-1的行，并将此行输出到“最优方案”的n+1行，依此类推，直到处理完第0期为止。

程序具体计算流程如图1所示。

对图1所示的计算流程的有关说明：

（1）S1：清除工作表。此步将“计算过程”除表头以外的内容清除，同时将“计算结果”中除表头和第0期以外的内容清除，以便存储重新计算的结果。“计算结果”表中第0期（第二行）是期初库存为V0时对应的参数，不参与循环计算，故不清除该行。

图1 计算流程

（2）S2：变量赋初值。通过此步，将程序用到的输入值赋给相关变量，主要有fr、fl、f1（初值2）、f2（初值2）、fl、n、Vnmax、Gd、Bd、h、M。

（3）S5：在jsgc的cells(fr，2)填充公式。

首先，自定义函数Vkmax()，其作用是返回第k期Vk的最大值，代码如下：

其次，通过如下的代码实现在Sheets（jsgc）.Cells（fr，2）中填充公式。

以上代码的作用是若在“计算结果”第6列查找到Vk_1则返回其成本值Fk_1_Vk_1，否则返回M。

（6）S17：通过此步可以产生多个最优解。

5 案例分析

以文献[4，7]的案例，利用本文提出的方法进行了验证。

文献[4]中Gd=3千元，Bd=1千元，h=0.5千元。表5是V0=0，Vnmax=3，Vn=0时的最优方案，图2是其对应的期量图。从表5和图2可见，在上述参数设置下第1和4期各安排了6台，其他各期均未安排生产计划，其总成本最低，最低总成本是22.5千元。表6是V0=4，Vnmax=0，Vn=0的最优方案，可见，因计算期初已有4台产品，可满足第1、第2期的1+3=4台产品需求，使最优方案总生产量由12台减少为8台，相应的总成本由22.5万元减少到18.5千元。表7是V0=0，Vnmax=3，Vn=2时的最优方案，可见，为满足Vn=2的目标，使生产总量由12台增加到14台，生产成本由22.5千元增加到27.5千元。表8是Vnmax=0，Vn=0，U3＜D3时的最优方案，可见，由于第3期的需求量大于其生产能力，使第2期提前生产超过其需求的量6-3=3以弥补第3期生产能力的不足。表9是V0=0，Vnmax=0，Vn=0，Uk不相同时的最优方案，图3是其对应的期量图。从表9可见，各期的生产能力Uk不同，最优方案中各期生产量Xk不超过Uk。由于Uk有所减小且各期不同，使安排生产的期数由2期增加到5期，各期生产量较接近Uk，表明更有效利用了每期的实际生产能力。表10是h=1千元时的最优方案，与表5相比可见，若单位存储成本上升到一定程度，会使原来在前期安排的生产计划后期推迟，安排生产的期数增加，至于具体推迟到哪期，则取决于批固定成本Gd、单位变动成本Bd及各期生产能力Uk的相对关系，但可以肯定的是，最优方案对应的批固定生产成本的增加值必小于等于存储成本的减少值；相反，可以预见，随着批生产成本Gd增加，会使安排生产计划的期数减少，最优方案对应的批固定生产成本的减少值必大于等于存储成本的增加值。

表5 文献[4]最优方案

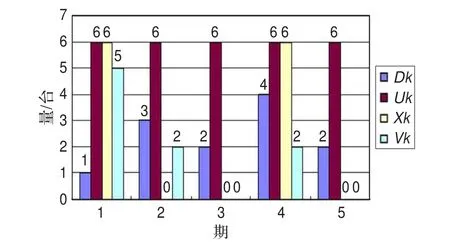
图2 Uk=6时期量图

表6 文献[4]V0=4时最优方案

文献[7]中Xk取值范围为0～2 500件，范围过宽，组合量巨大，使计算量过大，时效性差，另一方面也没有必要使Xk从0～2 500件进行遍历，故需对该案例进行“数据变换”。变换方式如下：找出各期需求量及生产能力约束的公约数（建议取最大公约数），将各期需求量和生产能力约束上限除以此公约数，将单位变动成本Bd、单位存储成本h乘以此公约数，计算结果中Xk、Vk则需乘以此公约数进行反变换。基于以上思路，文献[7]计算过程中取Gd=5万元，Bd=100万元，h=5万元。表11、表12是文献[7]的两个最优解。

表7 文献[4]V0=0，Vn max=3，Vn=2时最优方案

表8 文献[4]V0=0，Vn max=0，Vn=0，U3＜D3时最优方案

表9 文献[4]V0=0，Vn max=0，Vn=0，Uk不相同时最优方案

图3 Uk不相等时期量图

表10 文献[4]V0=0，Vn max=0，Vn=0，h=1时最优方案

表11 文献[7]最优方案一

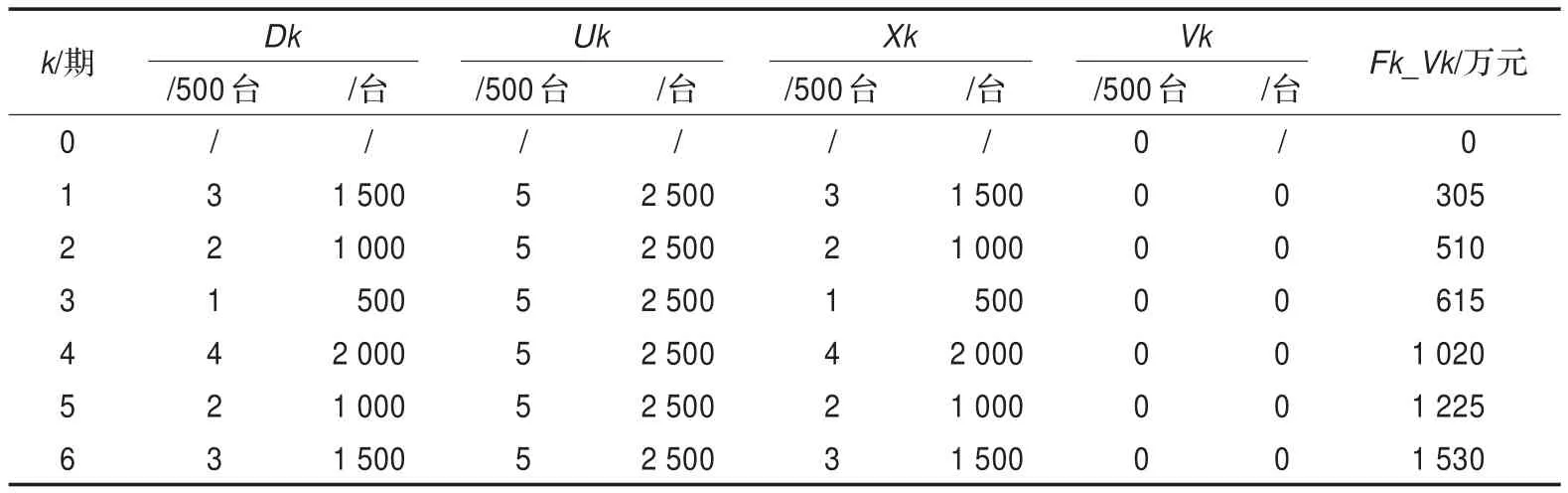
表12 文献[7]最优方案二

6 结论

将文献[4]的综合生产计划优化问题进行了改进从而拓宽了其应用范围，针对改进后的一类综合生产计划优化问题，通过对原数学优化模型和动态规划过程进行改进，形成了新的数学优化模型和动态规划过程，在此基础上以Excel为开发平台，提出了一种计算机辅助求解方法，最后通过案例研究验证了本文方法的有效性。研究结果表明，本文方法是有效的，具有较强的理论意义和应用价值。

[1]陈杰，潘卫刚.VMI策略下的综合生产计划研究[J].运筹与管理，2004，13（3）：137-140.

[2]黄景平，李彤，冯珊.企业综合生产计划的一种设计及优化方法[J].华中理工大学学报，1999，27（1）：7-10.

[3]于丽英，杨雷.生产计划的双目标混合整数规划模型及其求解[J].上海交通大学学报，2001，35（7）：1100-1102.

[4]甘应爱，田丰.运筹学[M].北京：清华大学出版社，1999：227-230.

[5]林中伟，谢强.基于遗传算法的多级有限能力生产计划[J].小型微型计算机系统，2003，24（1）：123-126.

[6]吕志民，宋肖青，董绍华.钢铁联合企业中期生产计划建模及算法[J].计算机集成制造系统，2011，17（1）：89-94.

[7]李怀祖.生产计划与控制[M].北京：中国科学技术出版社，2010：125-128.

[8]秦宣云.基于优先缺货权的工厂生产计划的动态规划模型[J].系统工程，2002，20（4）：20-24.

[9]李嫦，赵磊，赵晓波.组装线生产计划和库存策略的优化[J].清华大学学报：自然科学版，2010，50（5）：669-672.

[10]王鸿儒.Excel VBA程序设计[M].北京：中国铁道出版社，2005.

[11]王成春.Excel VBA 2003程序设计实例导航[M].北京：中国铁道出版社，2005.

ZENG Qiang1,SHEN Ling2,WU Liyun1,LAN Jianyi1

1.School of Energy Science and Engineering,Henan Polytechnic University,Jiaozuo,Henan 454000,China
2.School of Safety Science and Engineering,Henan Polytechnic University,Jiaozuo,Henan 454000,China

An improved method to optimize aggregate production planning based on dynamic programming is proposed. The aggregate production planning problem given from page 227 to page 230 in the book“Operation Research”editored by Gan Ying’ai is taken as the subject investigated in this paper.The shortage of the original optimizing problem of aggregate production planning,mathematic optimizing model,dynamic programming process and computation method is analyzed deeply in sequence and the corresponding improved measures are proposed for them.The effectiveness of the proposed method is tested by case study.

dynamic programming;aggregate production planning;computer optimization method

A

TP391；C93-03

10.3778/j.issn.1002-8331.1210-0022

ZENG Qiang,SHEN Ling,WU Liyun,et al.Improved method to optimize aggregate production planning based on dynamic programming.Computer Engineering and Applications,2014,50（21）：248-253.

国家自然科学基金（No.51104056）；河南省教育厅科学技术研究项目（No.12B120005）；河南理工大学博士基金资助项目（No.B2011-088）。

曾强（1975—），男，博士，副教授，研究领域：工业工程、生产管理；沈玲（1980—），女，讲师，研究领域：安全工程、工业工程；吴立云（1972—），女，在读博士，副教授，研究领域：工业工程；兰建义（1972—），男，在读博士，副教授，研究领域：工业工程。E-mail：zengqiang@cqu.edu.cn

2012-10-08

2012-12-19

1002-8331（2014）21-0248-06

CNKI出版日期：2013-01-11，http://www.cnki.net/kcms/detail/11.2127.TP.20130111.0951.002.html