基于分布估计算法的配电网故障区段定位

柳涛，彭敏放，宋丽伟，王岳明，沈美娥

1.湖南大学电气与信息工程学院，长沙 410082

2.北京信息科技大学计算机学院，北京 100101

基于分布估计算法的配电网故障区段定位

柳涛1，彭敏放1，宋丽伟1，王岳明1，沈美娥2

1.湖南大学电气与信息工程学院，长沙 410082

2.北京信息科技大学计算机学院，北京 100101

传统的人工智能算法在配电网馈线故障定位中的应用广泛，存在初始种群规模大，迭代次数多以及易陷入局部最优等缺陷。提出一种基于分布式估计算法的配电网故障区段定位方法，该方法将故障区段向量作为正确解，通过建立解空间内个体分布的概率模型，对模型采样，逐步提高最优故障区段向量在解空间内出现的概率。仿真结果表明将分布估计算法应用于多源开环条件下的配电网故障区段定位有着较快的故障定位速度和良好的容错性。

故障定位；配电网；分布估计算法

1 引言

配电网故障定位是实现配电自动化的基础，随着城网改造的进行，对于供电可靠性要求比较高的场合，都要求配有故障自动定位、隔离和恢复系统。目前我国的配电区域按照设施的完善与否可分为可测控区和不可测控区。对于监测和通讯设备不够完善的不可测控区，目前的定位方法主要有基于用户投诉信息的粗糙集故障定位法[1]。而对于配备了馈线终端单元（FTU）可测控区域，可根据FTU上传的信息判断出故障区域。目前这一方面采用的算法主要分为两大类：直接算法[1-3]和间接算法[4-14]。最典型的直接算法为矩阵算法。矩阵算法通过对网络拓扑结构矩阵进行运算，得出故障判定矩阵，该方法结构简单，容易实现，但是对FTU上传的故障信息序列的精确度要求较高，当FTU所处环境比较恶劣的时候，信息在传输的过程中易发生丢失和畸变，容错性较差，造成误判，危及配电网的安全可靠运行。间接算法就是把故障定位问题转化为寻优问题，即通常所说的0-1整数规划问题，找出最能解释故障信息的那个解。常用的间接算法主要有遗传算法[5-6]、蚁群算法[7-9]、神经网络[10]、petri网[11-12]、EM算法[13-14]等。此类算法大都具有较好的容错性，能够在信息发生畸变缺失的情况下准确进行故障定位。但普遍存在初始种群规模大，迭代次数过多，正确率不高的问题。

不同于遗传算法、蚁群算法等启发式人工智能算法对于生物进化微观上的数学建模，分布估计算法[15]是对于生物空间整体宏观上的分析，最大程度地保持了种群信息的完整性，通过优良解集的概率分布来指引进化搜索的前进方向，可以避免传统遗传算法中交叉、变异算子带来的随机性，从而提高算法跳出局部最优和摆脱搜索盲目的能力。目前已经在随机系统的故障诊断[15]以及输电网的扩展规划[16]、数传资源配置优化[17]、巡航导弹航迹规划[18]和动态多模问题[19]中得到了应用。同时分布估计算法原理简单，实现方便，鉴于配电网络拓扑结构比较复杂，而分布估计算法对于处理高维二进制离散问题具有较为理想的效果，因此将分布估计算法应用于配电网故障区段定位，并结合模块分割的思想，可以有效地提高配电网故障区段定位的准确性和效率。

2 分布式估计算法

分布估计算法[20]的基本思想是从已有种群中选取部分优良解，并利用这些优良解估计和学习染色体中基因的分布模型，然后采样该分布模型产生新的染色体和种群进行逐次迭代，最后逼近最优解。

分布估计算法按照概率模型的复杂程度可以划分为与变量无关的PBIL、UMDA、cGA算法，双变量相关的MIMIC、BMDA算法和多变量相关的ECGA、FDA、BOA等算法，总体来说，各种算法的实现过程主要分为以下两个部分：

（1）构建能够描述解空间的概率模型，通过对于种群个体适应度函数的计算选择出相对比较优秀的种群个体，然后利用统计学习的手段生成一个描述当前解集空间的概率模型。

（2）由概率模型随机采样产生新的种群，一般采用蒙特卡罗方法，对概率模型采样得到新的种群。

大致的流程可以分为：

（1）随机产生M个个体作为初始种群。

（2）计算M个个体的适应值，如果符合终止条件，算法结束，否则继续进行。

（3）进行选择操作，选择若干个个体作为优势群体。

（4）由优势群体构建概率模型，估计联合概率分布。

（5）从概率向量中采样若干次，得到新一代群体。

3 配电网故障区段定位的基本原理

3.1 问题描述

当配电网发生故障后，安装于分段开关和联络开关处的馈线故障终端（FTU）可以检测到流过的故障电流，在和预先整定过的故障电流定值进行比较后，将带时标的故障报警信息上传给控制主站，1表示开关处有故障电流流过，0表示无故障电流流过，配电网故障区段定位的过程实际上就是对安装在各个节点处的FTU上传的离散故障信息序列进行运算从而得出最佳故障区间的过程，因此故障定位的过程实际上是一个具有0、1约束的优化问题[13]，以相邻装备之间的区段作为独立设备，各设备的状态信息即为式（1）的优化参数X，通过将经过开关函数运算获得的馈线节点故障状态信息与FTU上传的电流越限信息进行逼近，确定馈线发生故障的区段。其数学模型可表示为：

其中n为参数变量的维数；f(x)为目标函数值；x(i)为参数变量第i维的值。

配电网故障区段定位的大致流程图如图1。

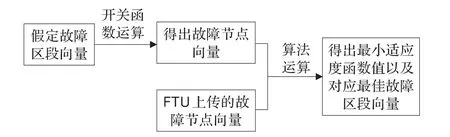
图1 故障定位原理图

3.2 单电源辐射状配电网的开关函数

开关函数应用于由假设故障区段求解各测控点状态值过程中，反映了设备信息与FTU等自动化设备终端设备上传的电流越限信号之间的相互关系，是两者之间联系的桥梁。如图2是一典型的单电源辐射状网络。

图2 典型单电源辐射状配电网

本文采用文献[6]中建立开关函数的方法，针对图1配电网的拓扑结构所建立的开关函数的模型为：

式中L1～L6为区段设备的状态信息，故障时为1，非故障时为0；Z*(1)～Z*(6)为开关设备的函数，有故障时为1，无故障时为0，反应的是设备状态信息与开关设备信息之间的关系，∨表示逻辑或，在该开关函数中，Z*(1)的值与其后馈线上的设备L1～L6的值有直接关系，Z*(2)～Z*(6)的具体含义与Z*(1)一致。例如当故障区段向量L1～L6为[0 0 0 0 1 0]时，Z*(1)～Z*(6)经公式（2）计算值为[1 1 1 1 1 0]。

3.3 评价函数

评价函数可以反映假设故障和实际情况之间的误差，而配电网故障区间定位的关键在于建立合适的评价函数，误差越小，说明两者之间越接近，进而说明得到的故障区段越准确。本文算法的实现过程实际就是开关函数和越限信号之间的最佳逼近过程。其中评价函数采用下式：

此式分为两部分：前一项主要描述了通过计算得出的开关节点信息与实际上传的故障信息之间的接近程度，第二项加上了故障区间的状态值，体现了故障诊断理论中“最小集”的概念，如不包含第二项，函数将存在误判现象，具体参见文献[6]，其中n为开关设备数量，m为区间数，Zi为各开关设备期望的状态值，Z*i为各开关设备实际上传的状态值，x(k)为区段值，w为权系数，其取值为0.8[6]。如图2所示配电网，当故障区段向量为[0 0 0 0 0 1]时，依开关函数计算得出故障节点向量为[1 1 1 0 0 1]，如果此时FTU上传的故障节点向量为[1 1 1 0 0 1]，则可知最佳适应度函数值为0.8，而由故障区段向量可知为区段6发生故障。

3.4 畸变信息与缺失信息的处理

由于本文应用分布估计算法进行故障定位，具备一定的容错性，因此在故障定位结束以后利用得到的故障区段向量，通过开关函数进行逆运算，得出实际故障节点向量，与期望节点故障向量进行比较即可得出畸变节点。

对于缺失信息进行故障定位时对该缺失位进行补0或1，得出故障区段向量以后，若故障区段向量唯一，则故障定位结束，否则取适应度函数值比较小的，如果适应度函数值也相等，则取故障区段比较少的。

3.5 算法流程

配电网馈线故障定位实际上是一个针对0、1数据实现最优化的过程，利用开关函数将节点故障向量与故障区段向量联系起来，构建完适应度函数以后进行运算，得出最优故障区段向量。本文采用的是分布估计算法中的UMDA[21-22]，大致可以分为5部分。

（1）随机产生初始种群R，计算初始种群概率P。

通过均匀随机数的方法产生随机数为0～1之间的m行n列的矩阵R（m为种群数量，n为种群维数）。然后对矩阵的每个元素进行归一化处理，若R(i，j)≥0.5，R(i，j)=1，否则R(i，j)=0。定义初始概率向量P= (p1，p2，…，pn)表示各列基因位置取1的概率，则1-P表示该基因位置取0的概率。初始种群生成后计算初始种群的初始概率P。

（2）计算M个个体的适应度函数值，如果符合终止条件，算法结束，输出最优故障区段向量，否则继续进行。本文的终止条件设为：最优故障区段向量对应的概率达到100%。

（3）按照适应度函数值对所有种群进行从大到小的排列，选择L＜M个个体作为优势群体C，本文优先选取数量为原种群数量的一半，即L=M/2。

（4）利用L个优势个体建立概率模型，估计联合概率分布，本文采用均匀分布模型[20]。

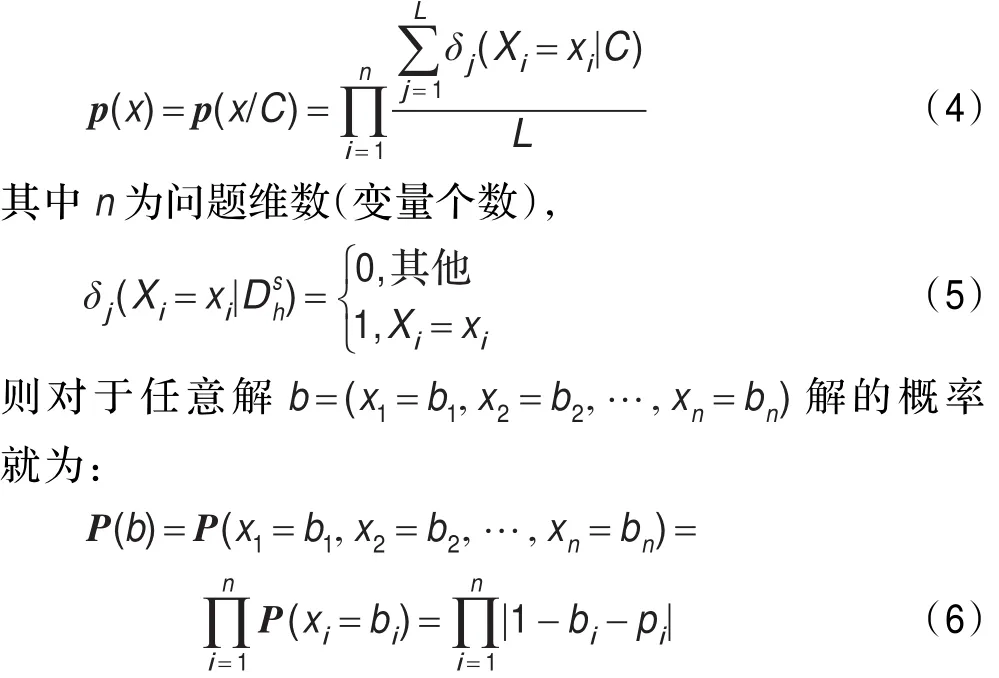
（5）从概率向量p(x)中采样M次，就可以得到新一代的种群。

一般的随机采样方法为蒙特卡罗分析法，本文为方便起见，对种群随机采样的方法采用如下公式方法，即符合要求，而且相比于蒙特卡罗法实现方便。

R(i，j)=ceil(rand()-P2(j))（7）其中R(i，j)为基因位上的数值，取0或1。rand()为随机产生的0～1之间的小数，P2(j)为对应列上基因取0的概率，ceil()函数在Matlab中表示向正方向舍入，当P2(j)=0.4时，则(rand()-P2() j)∈(-0.4，0.6)，取ceil函数后则R(i，j)取0的概率为0.4，取1的概率为0.6，可以保证采样的成功。

图3为算法的流程图，其中maxiter为整体迭代次数，K为当前迭代次数。

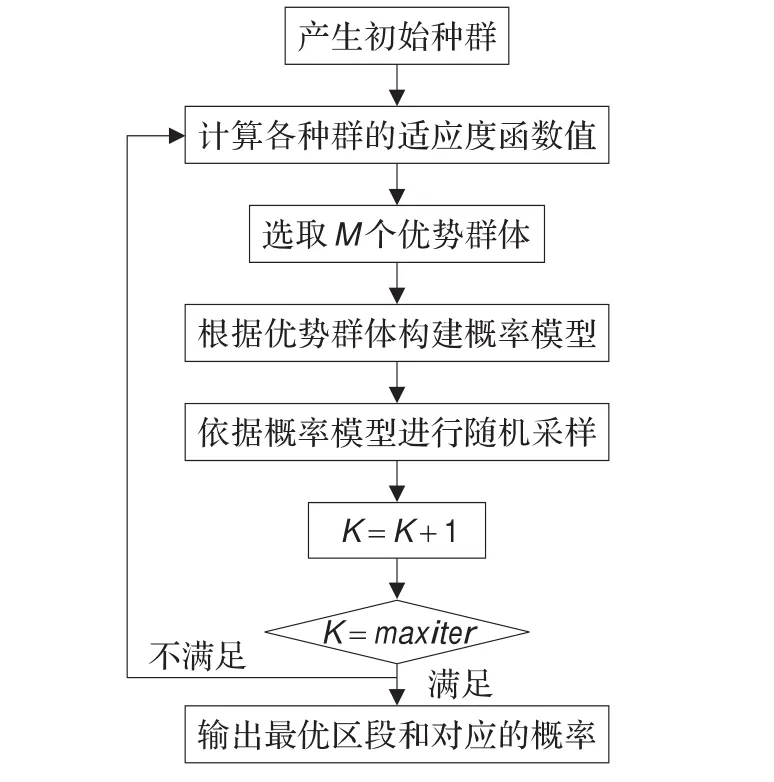
图3 算法流程图

图4 多电源环网开环运行配电网

表1 故障定位仿真结果

4 算例分析

4.1 故障仿真

配电网规模一般较大，区段定位效率不高。需要采用模块分割的方法，当故障发生后只对断路器动作的区域进行故障定位。以断路器和联络开关为界，将配电网络的拓扑结构划分为若干单电源辐射型配电网的叠加，当故障发生时，由于只对存在故障的区域进行运算，这样就大大降低了运算的复杂度，从而能够快速有效地进行故障定位[5]。

所以改进以后的评价函数模型为：

其中Ki表示权值，有故障时取1，无故障时取0，n为模块的数量。

图4是一个典型的多电源环网开环运行配电网的简化图，以断路器和联络开关为界分为4个独立区域，其中第一模块中包含了断路器1、分段开关2～7，第二模块分段开关8～11、16～17以及断路器12，第三模块为断路器15，分段开关13～14，剩余部分为第四模块。

目标函数可以定义为：

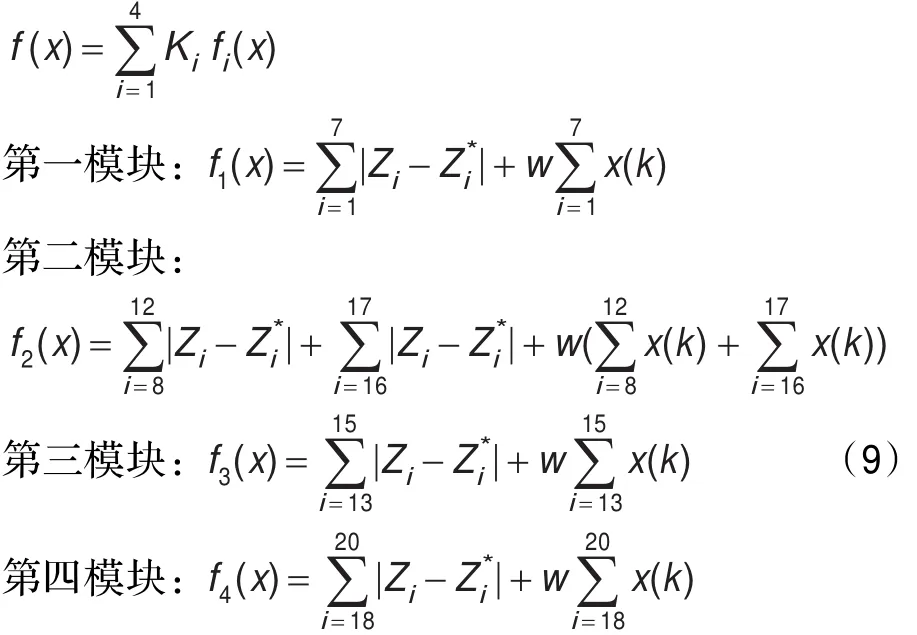
当进线断路器动作时该模块的Ki=1，否则为0。

针对单故障，多故障，信息畸变、缺失等几种情况进行仿真，结果如表1所示。

从表1分析可知，故障区段向量中的“1”代表该区段发生故障，对于1、2两种无畸变以及第3种两点畸变的故障定位，定位结果准确无误，第4种故障定位在缺失位补1或者补0，适应度函数值一致且故障区段也一样，而第5种故障定位中缺失位补1的情况下适应度函数值更小，因此得到区段7、9是真正的故障区段，由此可见，分布估计算法不仅可以对无畸变单区段故障、多区段故障实现准确定位，在信息发生畸变和缺失的情况下仍然可以进行有效故障区段定位。

上述五种故障定位，最优故障区段向量在每次迭代中出现的概率如图5中（a）～（e）所示。

4.2 算法性能比较

图5 最优故障区段向量在迭代中出现的概率

为了测试分布估计算法在配电网区段故障定位中的性能表现，分别运用遗传算法以及本文的分布式估计算法进行算例比较，两种算法初始种群随机产生，连续运行50次，遗传算法在种群数目比较少的情况下准确率不高，并且在得到最优解的情况下结果如表2所示，可以发现GA算法多次未搜索到最优解，尤其是在多区段故障的情况下，而分布估计算法的准确率则达到了86.6%，显示了较强的鲁棒性。

表2 分布估计算法与遗传算法应用比较

5 结束语

针对传统的人工智能算法在进行配电网馈线故障定位时种群数目较大，易陷入局部最优等缺陷，本文通过建立解空间中个体分布的均匀分布模型，利用提出的改进的采样方法避免了传统蒙特卡罗采样的困难，提高了算法的采样性能，通过单点和多点故障的仿真，显示了分布估计算法在进行配电网故障区段定位时准确、迅速和稳定的特点。

[1]梅念，石东源，杨増力，等.一种实用的复杂配电网故障定位的改进矩阵算法[J].电力系统自动化，2007，31（10）：66-70.

[2]王飞，孙莹.配电网故障定位的改进矩阵算法[J].电力系统自动化，2003，27（12）：45-46.

[3]杨俊起，陈滟涛，杨凌霄，等.配电网故障定位的改进矩阵算法研究[J].高电压技术，2007，33（5）：135-138.

[4]束洪春，孙向飞，司大军.基于故障投诉电话信息的配电网故障定位粗糙集方法[J].电网技术，2004，28（1）：64-70.

[5]郭壮志，陈波，刘灿萍，等.基于遗传算法的配电网故障定位[J].电网技术，2007，31（11）：88-92.

[6]卫志农，何桦，郑玉平.配电网故障区间定位的高级遗传算法[J].中国电机工程学报，2002，22（4）：127-130.

[7]王林川，张伟，张杰，等.基于改进蚁群算法的中压配电网故障定位[J].电力系统保护与控制，2008，36（22）：29-33.

[8]张颖，周韧，钟凯.改进蚁群算法在复杂配电网故障区段定位中的应用[J].电网技术，2011，35（1）：224-228.

[9]陈歆技，丁同奎，张钊.蚁群算法在配电网故障定位中的应用[J].电力系统自动化，2006，30（5）：74-77.

[10]孙雅明，杜红卫，廖志伟.基于神经逻辑网络冗余纠错和FNN组合的配网高容错性故障定位[J].电工技术学报，2001，16（4）：71-76.

[11]毕天姝，杨春发，黄少锋，等.基于改进Petri网模型的电网故障诊断方法[J].电网技术，2005，29（21）：52-56.

[12]孙雅明，吕航.Petri网和冗余纠错技术结合的配网故障区段定位新方法[J].中国电机工程学报，2004，24（10）：61-67.

[13]郭壮志，吴杰康.配电网故障区间定位的仿电磁学算法[J].中国电机工程学报，2010，30（3）：34-40.

[14]印峰，王耀南，杨易旻，等.结合变尺度法的改进类电磁机制算法[J].智能系统学报，2010，5（3）：254-259.

[15]王爱平，王宏.熵在随机系统故障诊断和容错控制中的应用[J].控制工程，2011，18（5）：655-659.

[16]侯云鹤，郑风雷，鲁丽娟，等.基于分布估计算法的输电网扩展规划[J].电网技术，2004，28（23）：32-37.

[17]常飞，武小悦.基于变邻域分布估计算法的数传资源配置优化[J].系统工程理论与实践，2011，31（8）：1546-1554.

[18]吴红，王维平，王磊，等.分布估计算法在巡航导弹航迹规划中的应用[J].电光与控制，2010，17（7）：6-10.

[19]Wu Yan，Wang Yuping，Liu Xiaoxiong，et al.Multi-population and diffusion UMDA for dynamic multimodal problems[J].Journal of Systems Engineering and Electronics，2011，21（5）：777-783.

[20]周树德，孙增圻.分布估计算法综述[J].自动化学报，2007，33（2）：113-124.

[21]Mühlenbein H，Paass G.Parallel problem solving from nature—PPSN IV[M].Berlin Heidelberg：Springer，1996：178-187.

[22]Mühlenbein H.The equation for response to selection and its use for prediction[J].Evolutionary Computation，1997，5（3）：303-346.

LIU Tao1,PENG Minfang1,SONG Liwei1,WANG Yueming1,SHEN Mei’e2

1.College of Electrical and Information Engineering,Hunan University,Changsha 410082,China
2.College of Computer Science,Beijing University of Information Science and Technology,Beijing 100101,China

The use of traditional artificial intelligence algorithm in distribution network feeder fault location is wide.But some shortcomings such as large initial population,too much iterations and falling into optimum exist.This paper puts forward the estimation of distribution algorithm to realize the fault location,in which the fault section vector is regarded as the right solution.By sampling from the individual probability model established in the solution space,the probability of the optimal fault section vector is gradually improved.The simulation result shows that the application of estimation of distribution algorithm in the fault section location in multiple source ring-open distribution network has faster speed and good fault tolerance.

fault location;distribution network;estimation of distribution algorithm

A

TM715

10.3778/j.issn.1002-8331.1212-0090

LIU Tao,PENG Minfang,SONG Liwei,et al.Distribution network section fault location based on estimation of distribution algorithm.Computer Engineering and Applications,2014,50（21）：243-247.

国家自然科学基金（No.60973032，No.60673084）；湖南省自然科学基金重点资助项目（No.10JJ2045）。

柳涛（1988—），男，硕士研究生，主要研究方向为电气设备在线监测与故障诊断；彭敏放（1964—），女，教授，博士生导师，主要研究方向为电气设备状态监测，智能信息处理，电磁场理论及其应用。E-mail：liutao20061988@126.com

2012-12-07

2013-03-07

1002-8331（2014）21-0243-05

CNKI出版日期：2013-03-29，http://www.cnki.net/kcms/detail/11.2127.TP.20130329.1540.013.html