造船监理员调度模型和混合遗传算法求解

符昊，葛洪伟，邵长鲁，朱亮

江南大学物联网工程学院，江苏无锡 214122

造船监理员调度模型和混合遗传算法求解

符昊，葛洪伟，邵长鲁，朱亮

江南大学物联网工程学院，江苏无锡 214122

有效快速地调度不同专业的造船监理员至不同厂区进行监理工作可以提高船舶建造效率，确保船只建造质量。针对我国造船监理公司监理员调度方面缺乏通用模型和调度手段落后的问题，建立起带有一系列硬性约束和软性约束的数学模型。随后针对该数学模型采用了基于模拟退火遗传算法的混合遗传算法进行求解。模拟仿真实验表明该模型与算法取得了理想效果。

造船监理员调度；船舶建造；人员调度；混合遗传算法；NP问题

1 引言

我国作为全球最大的造船国，据初步统计，在2011年度中国全年造船完工量约为6 800万载重吨，占全球份额的42.5%。这为我国造船业下一步技术创新和产业升级打下了良好的基础。由于船舶建造的工艺复杂，耗资巨大，施工的周期长，对其建造过程进行监理就成为必不可少的环节[1]。通常船东会委托监理公司进行船舶建造的监理工作以确保船舶建造质量。监理人员涵盖船舶建造中所涉及的各类专业，分别有船体、船机、船电和特殊专业工程技术人员，这里的特殊专业工程技术人员是根据船舶的主要工作性能来决定的[2]。为满足不同厂区在船舶建造过程中对不同专业造船监理员需求的变更，监理公司需要在船舶建造的每个阶段对公司内的各专业监理员重新合理调度。每个厂区对各专业监理员数量的需求和调度开销少这些硬性约束是每次调度应当满足的。为实现调度的人性化，监理员之间的默契程度以及他们对厂区的偏好这些软性约束也应予以关注。因此造船监理员调度问题是较为复杂的组合优化问题，属NP问题。

迄今为止，监理公司调度监理员的方式依旧是传统的手工调度。这样调度效率较低，人工成本高，考虑的方面有限，往往不能很好地满足实际的需求；尤其是在待调度人员人数多、调度情况复杂的时候，人工调度难以实施；所以利用计算机实现自动化调度是未来发展的目标。关于人员分配和调度的组合优化的问题，国外起步较早，研究较多。近年来，如Sabar、Montreuil和Frayret对装配中心员工调度的研究[3-4]、Ozgur等人对产业部门人员分配的探究[5]以及Ruibin等人对护士排班问题的研究[6-7]等等已研制出多种基于软计算的方法。但国外为相关问题建立的模型有较强的西方国家特点，与国内管理存在差异。我国对这方面问题的研究起步较晚。直到近年国内才出现例如任守纲等人从我国软件开发企业角度针对软件项目人力资源调度的研究[8]；沈吟东等人针对护士排班问题采用贴合实际护士排次类型和排班约束建立适应中国国情的问题模型[9-10]等。但他们考虑的问题较为简单，算法执行效率也有待改进。

针对造船监理员调度的研究至今国内、外鲜有报道。对于造船业，有独特的行业特殊性，如果只是简单地套用其他行业的相关研究则难以满足企业需求。本文通过对国内造船业现状的了解分析，考虑了对于造船业具有普遍适应性的监理员调度问题。在同时考虑硬性和软性约束的基础上，建立了一个适应我国造船监理公司监理员调度问题的整数规划（ILP）模型。并针对此问题采用了模拟退火遗传算法进行仿真实验求解，实现了对模型和求解算法的验证。

2 造船监理员调度问题描述

本文研究的造船监理员调度问题是指：给定一个调度周期内的全部可调度的造船监理员及每名监理员掌握的专业；给定在该周期内全部厂区对各专业监理员的需求数目。要求在基本满足所有厂区所需监理员数目的情况下（考虑到现实中临时员工的存在，允许出现需求数目超出可调度监理员数目的情况），编制出一个最有效（即满足硬性约束和软性约束）的造船监理员调度方案。为了方便管理并且考虑到“一人多专”的情况，要对不同专业的监理员进行统一调度，因此使得该问题变得复杂。

根据船舶建造监理的普遍特性，本文设定：

每名监理员在一个调度周期内只允许调度一次；每名监理员掌握的专业在一个调度周期内是固定不变的；对每名监理员的调度都应以满足厂区对特定专业监理员数量需求为前提；调度应考虑每名监理员的地域偏好和他们之间的人际关系。

假设一个调度周期为一个月，对于给定n名造船监理员的一个调度方案可以用一张二维表格表示（见表1）。其中第一行表示监理员的编号，第二行表示该监理员被派遣去往的厂区编号。

表1 2012年5月XX船舶建造监理公司员工调度方案

如表1中的方案满足设定的要求，则为可行方案，否则为不可行方案。同时，要找出可行方案中开销最少的最佳方案。

3 造船监理员调度问题建模

针对上述从实际工作中提炼出的造船监理员调度问题，首先建立一个考虑硬性约束的整数规划（ILP）模型，然后建立更人性化的扩展模型，使其能够反映造船监理员间配合默契程度以及他们对工作地点的偏好。

假设在一个调度周期内共有n位造船监理员，掌握μ类专业，共含有m个厂区。记E={1，2，…，n}表示造船监理员集合。F={1，2，…，m}表示该船舶建造公司拥有的厂区的集合。njk表示第j号厂区对掌握第k号专业造船监理员的需求数量。T是一个n×m的矩阵，tij代表第i号造船监理员前往第j号工厂所耗差旅费；O是表示造船监理员所属专业的矩阵，oij=1表示造船监理员i掌握第j号专业，否则等于0。调度决定变量xij定义为：

基于以上的记号，建立造船监理公司监理员调度问题的ILP模型如下：

在组合优化问题中，采用罚函数和奖励函数是一种可行且非常流行的方法。这种方法的思想是将有约束的优化问题通过在目标函数中引入罚函数或者奖励函数来对破坏约束的情形进行惩罚或者对满足约束的情形进行奖励，从而将原目标问题转化成没有约束的组合优化问题。转化后的目标函数格式一般为：

其中λ是与惩罚函数或奖励函数相关的系数，φ(gπ(X))用来评判破坏约束或者满足约束的程度。因此，对于本文要研究的问题中的硬性约束，可以使用奖励函数解决。

即要研究的只考虑硬性约束时的目标函数。由于每名监理工将作为特定单一专业工种的单位进行调度以满足实际需求，所以在求解本目标函数过程中对于掌握多种专业技能的监理员会自动淘汰其不大满足调度需求的专业，保留其最佳专业进行调度。

为了使得调度人性化，下面将进一步考虑监理员之间默契程度和监理员对工作地点的偏好，建立一个造船监理员调度问题扩展模型。

在日常生活工作中，监理员之间的默契程度并非一致。有些监理员之间配合默契，工作效率高；相反，有些监理员之间关系不佳，在一起共事可能会造成不必要的损失。监理员间配合默契程度是衡量不同监理员分配在同一厂区工作时相互合作的效率和服务质量的指标。相应管理人员可以针对实际情况（例如根据实际的利润和损失等）对某些监理员之间的默契关系进行量化，对默契程度特别佳的给定一个正值，对默契程度尤为不好的给定一个负值，而对其他默契程度不突出的设为0。在极端的情况，监理员两两之间默契程度都不为0，这时候监理员之间默契程度用一个n×n的矩阵R表示；对于一般情况，表示造船监理员间默契程度的R是一个稀疏矩阵。从而对于任意调度方案，都可以对每个厂区计算分配到该厂区监理员之间默契程度的总和，再汇总求和计算出该调度方案下默契总值p。

造船监理员对工作地点（即厂区）的偏好是指允许监理员根据自己的身体状况、家庭状况、作息习惯和风俗习惯等多方面因素，自行确定对工作地点（厂区）的偏好，以供制作调度方案时参考。监理员对于厂区的偏好程度也分为正值、0和负值。表示监理员对厂区的偏好程度的是一个n×m的矩阵，用L来表示。

监理员之间默契程度和他们对工作地点的偏好程度这两个约束属于软性约束，考虑上述约束将有助于提高他们工作的积极性和质量。为了不降低获得可行解的机会，它们将被转化到目标函数中：用目标函数式（6）替代式（5）。于是得到一个扩展的造船监理员调度问题模型。

其中lij表示第i名监理员对第j个厂区的偏好程度；α和β分别为造船监理员对工作地点偏好和造船监理员间默契程度的权重系数，其值由相应管理人员根据实际情况赋值。

4 基于模拟退火遗传算法的问题求解

4.1 模拟退火遗传算法

遗传算法（Genetic Algorithms）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法[11-12]。遗传算法广泛应用于传统搜索方法难以解决的高度复杂的非线性领域，且在组合优化方面展示了良好的优越性。因此，将遗传算法应用于本文研究的问题是可行的。

虽然遗传算法是一种通用的全局优化算法，但是遗传算法局部搜索能力却较差。而遗传算法中每一代群体的优良度直接影响后代的优良度与整个算法的效率。大量的研究表明遗传算法性能可以通过结合局部搜索步骤进行改善。这样的算法通常被称作“混合算法”[11]。模拟退火算法（Simulated Annealing）是基于Monte Carlo迭代求解策略的一种随机寻优算法，其出发点是基于固体物理退火过程与组合优化之间的相识性，模拟退火算法由某一较高温度开始，利用具有概率突跳特性的Metropolis抽样策略在解空间中进行随机搜索，伴随温度不断下降重复抽样过程。固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小，模拟退火算法是一种局部搜索能力很强的算法[13]。将模拟退火的思想引入遗传算法，对交叉和变异后的个体实施Boltzmann接受策略，不但增强了遗传算法的全局收敛性，并且使遗传算法在进化后期有较强的爬山性能，加快了进化后期的收敛速度，形成模拟退火遗传算法，可以有效缓解遗传算法的压力[14-15]。针对本文研究的问题，将遗传算法与模拟退火算法结合起来，使用模拟退火遗传算法，以提升遗传算法局部搜索能力，从而对性能进行改善。

4.2 基于模拟退火遗传算法的问题求解流程

本文采用实值编码方式，个体长度为待调度的造船监理员人数，其中个体中每个元素的值表示该监理员被派往的厂区。这样的编码方式可以自动满足约束式（2）。

本文研究的问题一个主要方面是差旅费开销。根据实际情况，在一次调度前可以知道上一个调度周期所有待调度监理员所处的厂区和此次调度周期厂区对监理员相应需求情况。根据这些数据，用计算机可以快速计算出哪些厂区对哪些专业监理员需求人数超出已有人数（即本次调度前已在此厂区的相关监理员人数），而这些厂区的相应监理员是无需调度到其他厂区的。这样在不考虑软性约束时事先确定哪些造船监理员不必要调度到其他厂区，从而能生成让这些监理员原地待命的初始群体。同时为保证初始群体的多样性，随机生成其他监理员所派往的厂区编号。并且为更好地考虑到软性约束，随机选取任意“原地待命”的监理员，随机生成他们所派往的厂区。这样启发式生成初始种群的优势是能生成性能较好的个体，提高算法的进化速率。虽然启发式生成初始种群可能会增大运行开销，但是实验表明，这部分开销在研究的问题整体规模中是极小的且可接受的。

一般来说，遗传算法中适应度计算最费时间，而且需要不断产生新一代，每一代又有若干个体，提高遗传算法的运行速度显得尤为重要。由于遗传算法的内在并行机制，并行处理将有效地改善遗传算法的性能。迁移（migration）是并行遗传算法引入一个新的算子并在进化过程中使子群体互相交换个体的过程[14]。本文将使用迁移策略将子群体中最好的个体发给其他的子群体，通过迁移可以加快较好个体在群体中的传播。算法流程如下：

步骤1输入监理员数量n、厂区个数m；输入差旅费矩阵T、专业矩阵O，人际关系矩阵R及地点偏好矩阵L内元素的值。

步骤2启发式方法生成初始群体；输入遗传算法配置参数；设定初始温度tmax终止温度tmin，温度下降率ν，t=tmax以及局部搜索参数w等运行参数。

步骤3采用遗传算法对种群进行交叉、变异、非线性排序和选择。

步骤4对于种群中的每个个体调用模拟退火算法。

步骤5更新温度if(t＞tmin)thent=t*ν；否则算法结束，输出调度结果。

步骤6转到步骤3。

5 实验结果及分析

仿真环境的运行平台为Matlab，在Core i5 2.3 GHz的CPU和4 GB RAM的PC上运行。为了方便说明和验证，选用一组规模较小并且典型的数据进行测试。假设共有15名造船监理员，掌握5个不同的专业，其中一位监理员同时掌握两个专业；共有5个厂区。设定在调度前15名监理员平均分配到5个厂区。根据现实中机票价格，设定表示15名监理员的差旅费矩阵T为：

表示监理员之间默契程度的矩阵R为15×15的矩阵，令r1，15=-1，其他元素都为0；表示15名监理员地点偏好的矩阵L为15×5的矩阵，其中l10，4=l11，4=1，l12，1=-1，其他元素值为0；表示监理员掌握专业的矩阵O为：

本文使用的算法运行参数如表2和表3。

表2 求解过程中基本遗传算法使用的参数

表3 求解过程中有关子种群和迁移使用的参数

从算法描述中可以看出，算法外循环执行次数与tmax，tmin和ν有直接联系。一般来说，tmax要取得足够大，使得能够接受劣解的概率比较大，在初始时能几乎100%的概率接受劣解。但由于本次实验数据规模较小，经过多次实验，最后采用的有关模拟退火参数如表4。

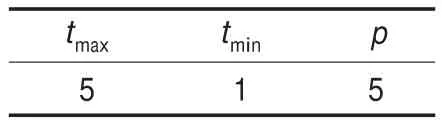
表4 求解过程中有关模拟退火相关参数

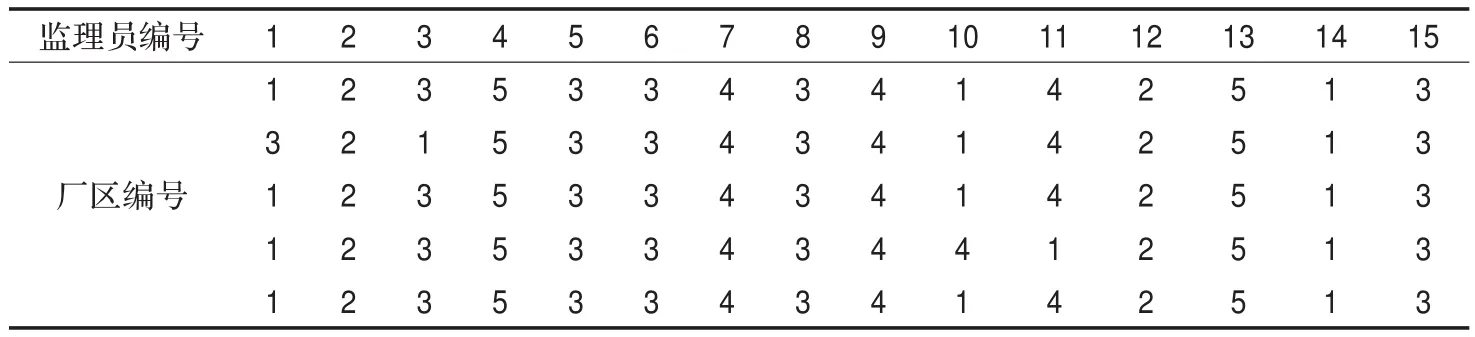
表5 仿真实验调度结果

从以上的参数和实验数据描述可以看出，第14名监理员同时掌握第4和第5号专业；而所有厂区对第5号专业监理员的需求是2，对第3和第4号专业的需求为4，对其他专业需求人数都为3；第1号表示不愿与第15号监理员共事；第10号监理员和第11号监理员更偏好第4号厂区，而第12号监理员不愿去第1号厂区。在接下来的仿真实验中将着重考察这些要求是否满足。

运行20次，平均耗时为3.57 s。图1给出了随机某次实验过程中最优解的变化，可以看出在较少的迭代次数内就可以获得较理想最优解。注意图中最优解的值只是本模型和算法得出的用于量化的值，并非真实费用开销。

图1 实验过程中最优目标函数解的变化

随机选取5次运行结果，实验结果（即调度结果）如表5所示。

从以上实验结果可以看出，对于硬性约束要求，调度结果都很好满足了厂区对各专业监理员人数的需求且没有出现“应留守却被调离”等这样的无意义调度；同时总差旅费是最少的，例如对于第6号监理员，如若人工调度可能凭感觉做出将第6号监理员继续留在第2号厂区的决定，但仿真实验结果表明，第6号监理员调度至第3号厂区并将第2号和第9号监理员分别调度至第2号和第4号厂区更加节省调度开销。除表5中第二个调度结果对第1号监理员与第15号监理员默契程度没有考虑周到外，其余调度结果都较好满足了有关人性化的软性约束要求，体现了调度人性化，如第10号至第12号监理员对特定厂区的偏好等要求都被充分满足。最优实验解和最差实验结果相比偏差约为0.635%，算法有较好的稳定性。

为验证系统的实用性，继续根据某监理公司实际情况进行仿真实验，每次调度的监理员人数达到百人。实验参数和变量因问题规模的增大而相应变大。实验取得理想结果。

6 结束语

本文是对我国造船监理公司监理人员调度问题的一个初步研究，旨在探讨一种系统解决针对实际造船监理公司监理人员调度问题的思路与方法。根据我国船舶建造监理的实际情况，归纳出一系列硬性约束和软性约束，并建立了一个较通用的造船监理人员调度的数学模型。同时所建立模型有较好的可塑性和可扩展性，不同的船舶建造监理公司可以依据实际情况将自身的独特要求以软硬约束的形式融入模型中。

在数学模型的基础上，宏观采用遗传算法对该问题求解，通过启发式生成种群和引入迁移策略改进算法效率，并引入模拟退火算法改进遗传算法的局部搜索能力。仿真实验验证了模型有效且算法有较好的执行效率和鲁棒性，具有一定的实用价值和经济效益。在未来的研究中，将进一步改善模型和算法。

[1]张莹.浅谈船舶监造的管理方法[J].中国水运，2010，10（8）：10-11.

[2]李海平.船舶建造工程的监理工作[J].中国水运：学术版，2010，6（2）：42-44.

[3]Sabar M，Montreuil B，Frayret J M.A multi-agent-based approach for personnel scheduling in assembly centers[J]. Engineering Applications of Artificial Intelligence，2009，22（7）：1080-1088.

[4]Sabar M，Montreuil B，Frayret J M.An agent-based algorithm for personnel shift-scheduling and rescheduling in flexible assembly lines[J].Journal of Intelligent Manufacturing，2012，23（6）：2623-2634.

[5]Kabak O，Ulengin F，Aktas E，et al.Efficient shift scheduling in the retail sector through two-stage optimization[J]. European Journal of Operational Research，2008，184（1）：76-90.

[6]Bai Ruibin，Burke E K，Kendall G，et al.A hybrid evolutionary approach to the nurse rostering problem[J].IEEE Transactions on Evolutionary Computation，2010，14（4）：580-590.

[7]Lu Zhipeng，Hao Jinkao.Adaptive neighborhood search for nurse rostering[J].European Journal of Operational Research，2012，218（3）：865-876.

[8]任守纲，徐焕良，李相全.基于遗传算法的软件项目人力资源调度研究[J].计算机应用研究，2008，25（12）：3563-3567.

[9]沈吟东，陈名晖，邓婕.利用矩阵向量化变换求解护士排班问题[C]//中国控制与决策会议论文集，2008：1019-1022.

[10]沈吟东，苏光辉.带约束的护士排班模型和基于变换规则的优化算法[J].计算机工程与科学，2010，32（7）：99-103.

[11]Krasnogor N，Smith J E.A tutorial for competent mimetic algorithms：model，taxonomy and design issues[J].IEEE Trans on Evol Comput，2005，9（5）：474-488.

[12]葛继科，邱玉辉，吴春明，等.遗传算法研究综述[J].计算机应用研究，2008，25（10）：2911-2916.

[13]曹云健，董晶.基于模拟退火遗传算法的服务选择[J].计算机工程与设计，2011，32（10）：3507-3510.

[14]Potts J C.The development and evaluation of an improved genetic algorithm based on migration and artificial selection[J].IEEE Trans on SMC，1994，24（1）：73-86.

[15]王银年，葛洪伟.求解TSP问题的改进模拟退火遗传算法[J].计算机工程与应用，2010，46（5）：44-47.

FU Hao,GE Hongwei,SHAO Changlu,ZHU Liang

School of Internet of Things Engineering,Jiangnan University,Wuxi,Jiangsu 214122,China

Quickly and effectively scheduling members of shipbuilding supervision of different majors to specific shipyards improves the efficiency of shipbuilding and ensures the constructional quality.Because lack of general models and effective scheduling means for above-mentioned issue in China,this paper establishes mathematical models with a series of hard constraints and soft constraints to solve this problem.Followed by the models,a hybrid genetic algorithm based on simulated-annealing genetic algorithm is applied to solving this problem.Simulated experiments verify that the model and the algorithm are feasible and effective.

scheduling shipbuilding inspectors;construction of ships;personnel scheduling;hybrid genetic algorithm;NPproblem

A

TP302.1

10.3778/j.issn.1002-8331.1212-0055

FU Hao,GE Hongwei,SHAO Changlu,et al.Models and hybrid genetic algorithm for scheduling shipbuilding inspectors.Computer Engineering and Applications,2014,50（21）：238-242.

符昊（1991—），男，本科，主要研究方向为人工智能；葛洪伟（1967—），男，博士，教授/博士生导师，主要研究方向为模式识别、人工智能和算法分析；邵长鲁（1988—），男，硕士研究生，主要研究方向为系统开发、资源调度；朱亮（1991—），男，本科。E-mail：haofu@ucdavis.edu

2012-12-05

2013-03-19

1002-8331（2014）21-0238-05

CNKI出版日期：2013-03-29，http://www.cnki.net/kcms/detail/11.2127.TP.20130329.1540.014.html