双缝干涉法测量金属的杨氏模量

方运良，崔 娟，朱伟玲

(广东石油化工学院 a.理学院；b.机电工程学院，广东 茂名 525000)

1 引 言

杨氏模量是表征固体材料在弹性限度内纵向抗拉或抗压性能的物理量，是选定机械构件材料的重要依据之一. 在工程技术中通常采用拉伸法测量金属材料的杨氏模量. 要准确测量杨氏模量，关键是如何精确地测量金属丝受力时的微小形变量. 金属材料的形变很小，例如1根长100 cm、直径0.580 mm的钢丝在10 N的作用下，伸长量只有0.2 mm左右，因此测量钢丝伸长量的误差约为μm量级. 实验教学中多采用光杠杆法、迈克耳孙干涉法、光的衍射法等进行测量[1-10]. 本文利用活动双缝干涉法精确测量钢丝在重力作用下的伸长量，从而准确测量金属的杨氏模量.

2 测量原理与装置

设一粗细均匀的金属丝，长度为L，截面积为S(直径为d). 将其一端固定，另一端沿金属丝伸长方向加一外力F，金属丝在外力F的作用下伸长了ΔL. 则应力F/S和应变ΔL/L满足胡克定律，即

其中，杨氏模量Y可表示为[11]

从(1)式可见，测量杨氏模量的主要问题是如何测准微小长度变化. 笔者设计了一个活动的双缝，利用杨氏双缝干涉可精确测量ΔL.

图1是杨氏双缝干涉示意图，波长为λ的激光照到双缝S1和S2上，双缝间距s，中点M到观察屏的距离MO=D，P为观察屏上任意一点，且PO=x，通常的观测条件是D≫s，D≫x，即θ角很小，根据波动理论可知，各级干涉条纹中心[12]到O点距离为

图1 杨氏双缝干涉示意图

两相邻明纹(或暗纹)的距离是

图2是活动双缝装置图. 用于产生干涉条纹的双缝在支架上可以自由滑动，固定缝通过调节丝杆固定在支架上(调节丝杆在一定的范围内，可以调节双缝缝间的宽度)，活动缝在支架上自由滑动且通过连接扣与钢丝固紧在一起. 活动双缝装置安装在常见的拉伸式杨氏模量实验仪中部的平台上，当给钢丝施加拉力时，钢丝伸长，带动活动缝下移，引起狭缝间宽度的变化，由此干涉条纹发生变化.

图2 测量装置示意图

实验时，调整狭缝间的宽度，使屏上出现干涉条纹. 测出双缝到屏的距离为D,相邻2条明条纹之间的距离为Δx0；加上砝码m后，测出相邻2条明条纹之间的距离为Δx1，代入式(2)计算出对应狭缝的宽度分别为s0和s1，则钢丝的伸长量为

由(1)式即可求出杨氏模量为

3 实验数据与结果

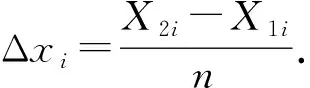
图3 实物摆放示意图

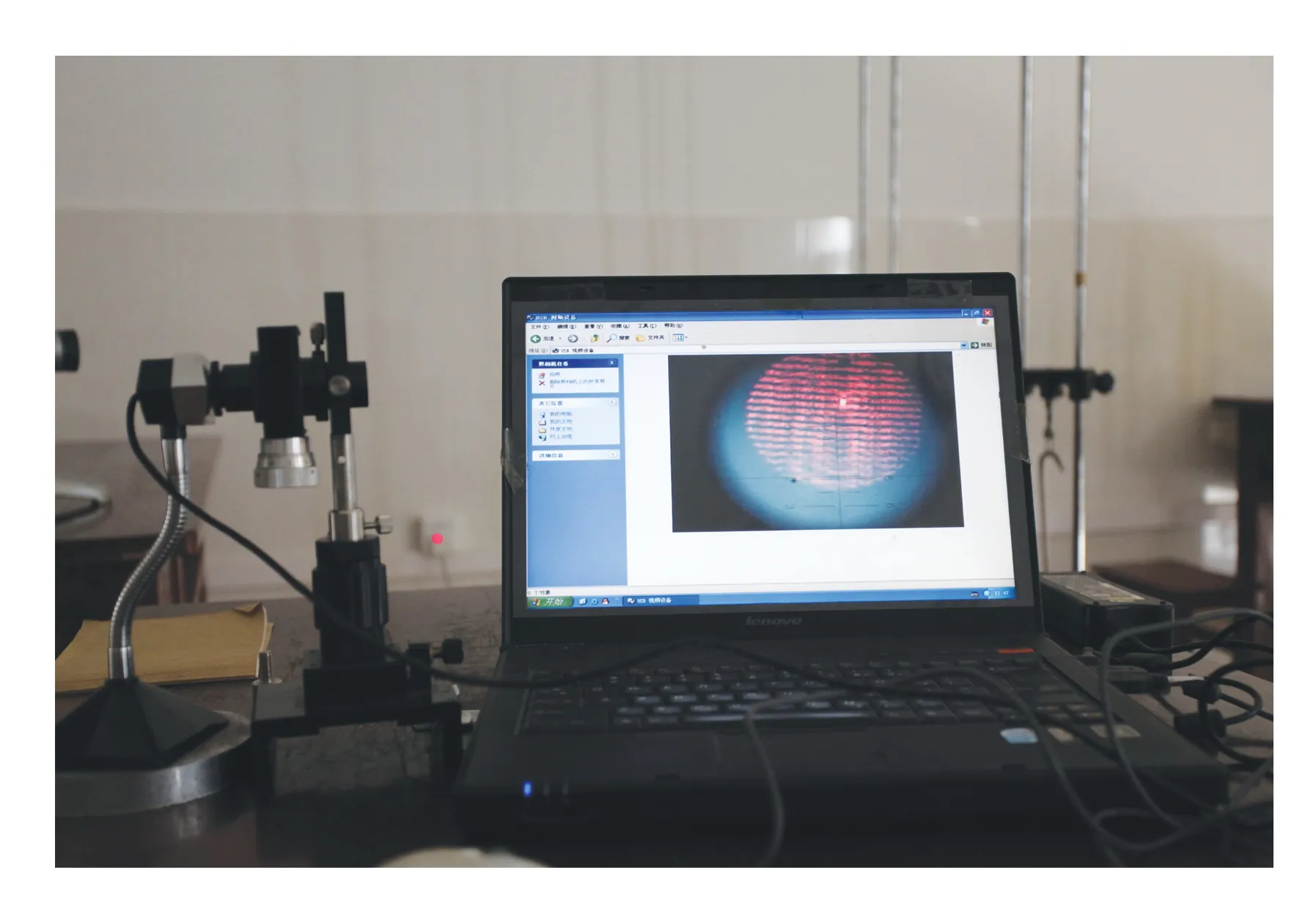
图4 干涉条纹图像

表1 不同拉力作用下的实验数据

U=YUr=0.01×1011N/m2.

从测量结果可以得出Y=(1.97±0.01)×1011N/m2,Ur=±0.2%，钢丝的杨氏模量Y值在钢质材质(Y钢=196～216 GPa)范围内[13].

由式(4)可知Y的不确定度与砝码质量m及L，d，D和Δx的不确定度的有关，又由式(2)知，两相邻干涉条纹距离Δxi与D及si有关. 在本实验中si是待测量，增加双缝到观察屏之间的距离D，干涉条纹之间的宽度Δxi增大，可以提高Δxi分辨率，在读数误差相同的条件下，可减小读数误差在Δxi中的相对误差，有助于si测量精度的提高，起到减小Y的不确定度的作用.

4 结束语

与传统的拉伸法测量杨氏模量相比，双缝干涉法克服了光杠杆法用望远镜读数困难的问题；与衍射法相比，双缝干涉法的计算过程简单，又是多倍数测量取平均值可减少读数误差. 若在测微目镜读数窗口处加装普通的CCD协助读数，不仅使观察到的干涉条纹的位置稳定不变，而且还能提高分辨效果，读数更方便直观. 本实验装置的双缝是用薄金属板刻制的，可以自由装卸. 当取下双缝薄片，此装置还可以做单缝衍射实验.

参考文献：

[1] 姜伟. 拉伸法测金属丝杨氏模量的研究[J]. 大学物理实验，1996，9(3):32-33.

[2] 侯德亭,王帅,王素红. 光的衍射法测量金属的杨氏弹性模量[J]. 信息工程学院学报，1997,16(2):51-533.

[3] 李彦敏，陈向炜. 光的衍射法测量杨氏模量[J]. 大学物理实验，1998，11(2):16-17.

[4] 麻福厚. 用惠斯通电桥测定杨氏模量[J]. 物理实验,1998，18(5):6-8.

[5] 王爱军. 用迈克耳孙干涉仪测量杨氏模量[J]. 大学物理，1999，18(9):30-31.

[6] 徐辑彦,关寿华. 金属丝杨氏弹性模量电测法初探[J]. 大学物理实验,2000,13(3):44-46.

[7] 史智平. 杨氏模量测量新方法[J]. 宝鸡文理学院学报(自然科学版),2000,20(3):233-235.

[8] 黄增光,马再超,卢佃清，等. 衍射法测量金属丝的杨氏模量[J]. 物理与工程,2008，18(5):27-30.

[9] 陈水波,乐雄军. 测量杨氏模量的智能光电系统[J]. 物理实验,2001，21(11):34-35.

[10] 吴立峰,杨广华. 基于PSD位置传感器的杨氏模量测量[J]. 五邑大学学报(自然科学版)，2004,18(2):18-21.

[10] 张帮,袁广宇,意志敏，等. 利用迈克耳孙干涉原理测杨氏模量[J]. 大学物理实验,2007，20(3):8-10.

[12] 杨述武,赵立竹,沈国土. 普通物理实验(一、力学、热学部分)[M]. 4版. 北京：高等教育出版社，2007:48.

[13] 程守株,江之永. 普通物理学(第3册)[M]. 5版. 北京：高等教育出版社，1998:175-176.

[14] 丁慎训,张连芳. 物理实验教程[M]. 2版. 北京：清华大学出版社，2002:14.