基于傅里叶变换的激光数字散斑测量平板玻璃的楔角

谭佐军，谢 静

（华中农业大学 理学院 应用物理系，湖北 武汉430070）

1 引 言

激光照射散射体表面产生漫反射或通过透明散射体时，在散射表面或附近光场中观察到的无规则分布的明暗斑点称为激光散斑.散斑现象普遍存在于光学成像的过程中，通过对散斑场的分析可以测量物体的一些物理特征值［1］.因此激光散斑计量技术成为现代光学重要的测量方法，主要有：直接照相法、双曝光法、电子散斑干涉法、错位散斑干涉法和散斑相关测量技术等.它具有全场、非接触、高精度、高灵敏度和实时快速等优点［2］，现已广泛应用于振动、位移、形变、断裂、粗糙度的测量，农业及生物医学等方面.因此激光散斑成像技术成为很多学校在教学实验中推广的一个实验，该实验的引入有利于学生了解激光散斑的特性及其在各个领域中的应用［3-4］.

平板玻璃是一种抛光后的相位物体，其表面光滑，不能产生激光散斑，因此无法直接利用激光散斑技术测量其微小楔角.我们在光路中借助能够产生激光散斑的元件（毛玻璃等），采用傅里叶变换的数字激光散斑技术测量了平板玻璃的微小楔角.该方法直观、快速、精度高，有利于学生了解激光光束的基本特点以及CCD光电成像系统的原理，通过实验学生还可以进一步巩固光的衍射、光的干涉、激光高斯光束特性、信息光学等相关知识.该方法也可以引导学生开拓思路，从而利用激光散斑技术对抛光物体进行位移和旋转等测量.

2 测量原理

基于傅里叶变换的数字激光散斑技术测量平板玻璃微小楔角的光路如图1所示.图1中M为毛玻璃，CCD放置于H处为记录激光散斑，W为带有微小楔角的平板玻璃.

图1 数字散斑技术测量平板玻璃楔角光路示意图

当平板玻璃W不在光路中时，激光束将直接照射毛玻璃，毛玻璃作为透明的散射体在其附近的光场中产生激光散斑.当把平板玻璃W放入光路中，由于微小楔角的作用，经过平板玻璃W出射后的光线将偏移α角度，假设光线1通过毛玻璃上的A点，而没有平板玻璃时光线2通过A点，这就意味着在没有平板玻璃W时，A点产生的散斑在位置2，加入平板玻璃后，A点产生的散斑就移动到1′处，位置2和位置1′间距为Δx，这就是1对散斑.因此H处的CCD就可以记录形成的散斑场.根据图1的几何关系，散斑位移量Δx和平板玻璃楔角θ的关系为［5］

式中z为毛玻璃到CCD之间的距离，n为玻璃折射率.

光路未加平板玻璃和加入平板玻璃2次记录的激光散斑强度分布完全相同，但是两者有相对位移x0，设未加平板玻璃CCD像面上散斑强度分布为A0（x0，y0），加入平板玻璃位移后的强度分布为AL（x0-Δx，y0），则2个散斑图叠加的光强可表示为

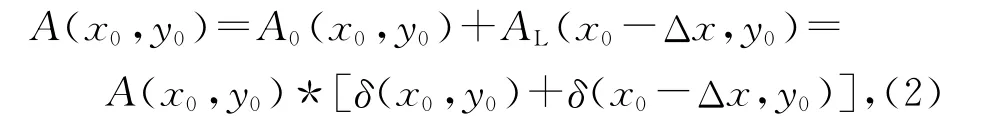
式（2）中＊表示卷积.对相加的散斑图进行傅里叶变换可得其频谱分布为［6-7］

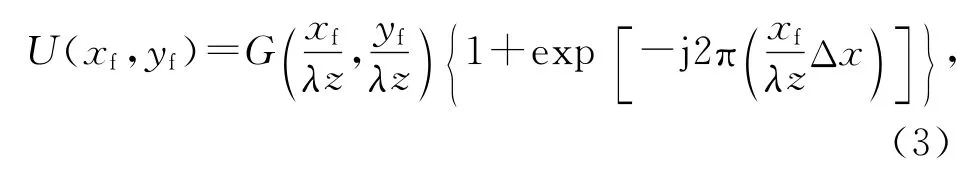
式（3）中λ为光波波长.光强分布可表示为

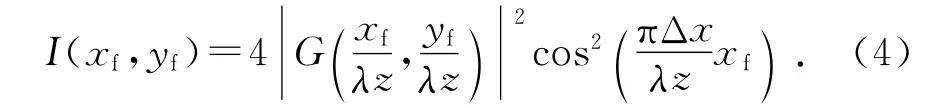
可见，在频谱面上观察到的光强分布是有散斑结构的杨氏双缝干涉条纹，条纹间距为

根据式（1）和式（5）可以得平板玻璃楔角的计算公式为

3 实验研究

3.1 散斑图像获取

按图1所示光路进行实验，系统中光源采用He-Ne激光器，波长为632.8nm，用1对偏振片进行光强调节.CCD采用AVT相机STINGAY系列F504B／C，该CCD分辨率为2 452×2 052像素，像元尺寸为3.45μm×3.45μm.首先在未放入平板玻璃时，用CCD采集激光束照射毛玻璃产生的散斑图，如图2（a）所示，然后放入平板玻璃，用CCD采集此时的散斑图，如图2（b）所示.

图2 CCD采集的激光散斑图

3.2 干涉条纹获取及分析

根据式（2）～（4）分析，在 Matlab中将图2中的图（a）和图（b）相加，相加后的结果进行快速傅里叶变换，可得频谱面上的光强分布，图3非常清晰地展现了有散斑结构的杨氏双缝干涉条纹.这也说明采用大图像高分辨率的CCD可以提高相关条纹场的信噪比［8］，降低了条纹处理的难度.

用与条纹图像维度相同的一维全1矩阵可抽取条纹图像x方向的光强分布图，如图4所示.由图4（a）可见，尽管获取了信噪比比较高的散斑杨氏双缝干涉条纹，但是仍然存在噪声的影响，曲线显出很多毛刺，这导致光强分布曲线出现不确定的极值点，不消除这些噪声就无法准确计算条纹间距.因此采用移动平均法对曲线进平滑处理，在此采用20pixel大小的移动窗口，处理结果如图4（b）所示.从图4（b）可见，平滑后的条纹分布曲线消除了条纹上毛刺，同时保证了条纹中心像素的位置不变.

图3 快速傅里叶变换获得的杨氏双缝干涉条纹

图4 光强分布曲线

3.3 干涉条纹间距的计算

用CCD记录散斑图，通过FFT获取干涉条纹，由于CCD成像系统及图像处理等因素导致存在系统传递函数，必须进行像素单位与实际尺寸之间的度量单位转换［9］.测得条纹间距为l′与实际的条纹间距l的关系为

式（7）中b是系统误差，通过2次标定就可以确定k和b.选用定标板，通过CCD成像系统，测得Y1占有的像元数N1，测得Y2占有的像元数N2，将Y1，Y2，N1，N2代入式（7），可得

4 实验结果及分析

在实验中分别用自准直法和激光数字散斑法对同1块平板玻璃进行重复测量.环境为室温，当CCD接通电源后约15min开始测量，以便CCD达到稳定的工作状态.表1为测试结果，l＝（2.966±0.003）mm，θ散斑＝1.420 6′±0.001 5′，θ自准直＝1.416′±0.017′.

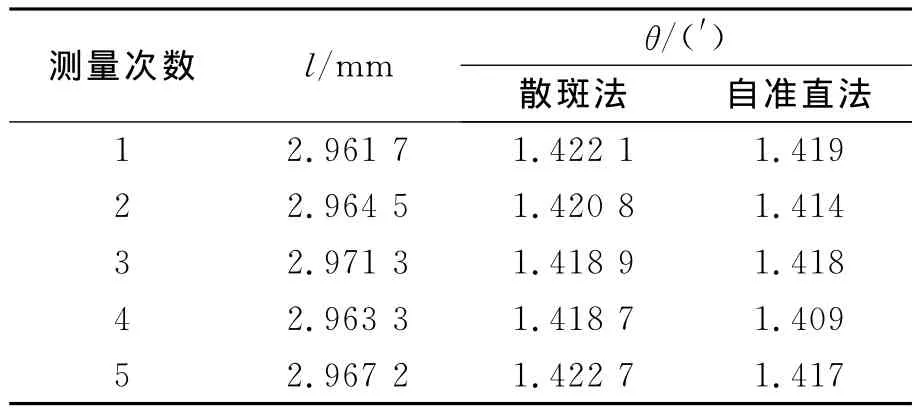
表1 测试数据

利用定标板中的1mm和2mm刻线确定k＝0.043 5mm／pixel，激光数字散斑法系统误差b＝0.001 2mm，激光器波长为632.8nm，平板玻璃折射率n＝1.516.作为5次重复测量的物理量，同时为了保证标准不确定度的置信水平，把平均值的标准偏差乘以t0.95（1.96）因子作为测量结果不确定度的A类分量，为了便于教学，将仪器误差按均匀分布近似处理，把自准直仪器误差除以作为自准直法的B类分量，自准直仪测量误差为1″.由表1可见，基于FFT的激光数字散斑法测量的结果与自准直法测量结果吻合较好，效果非常理想.

5 结束语

本文用傅里叶变换激光数字散斑图测量了平板玻璃的微小楔角.该方法测量参量少、光路简单、精度高、实验现象直观、效果好、实验操作简单，适合本科生的实验教学.学生可以从实验中进一步巩固光的衍射、光的干涉、激光高斯光束特性、信息光学等相关知识，加深了学生对激光散斑的成像原理以及应用理解.该方法也可引导学生开拓思路，利用激光散斑技术对抛光物体进行位移和旋转等测量.该实验可以激发学生的兴趣，促进学生向研究性学习和创新性学习的转变.

［1］Dainty J C.Laser speckle and related phenomena［M］.Berlin and New York：Springer-Verlag，1975.

［2］Sj¨odahl M.Electronic speckle photography：increased accuracy by nonintegral pixel shifting［J］.Appl.Opt.，1994，33（28）：6667-6673.

［3］王中平，张权，朱玲，等.CCD成像辅助激光散斑实验［J］.物理实验，2010，30（10）：11-14.

［4］黄水平，张飞雁.激光散斑在大学物理实验教学中的应用［J］.物理与工程，2011，21（1）：37-39.

［5］肖明海，王帼华.平板玻璃微小楔角的散斑法测量［J］.激光技术，1989，13（1）：42-45.

［6］吕乃光.傅里叶光学［M］.北京：机械工业出版社，2006：1-50.

［7］姚琨，陈蝶萍，张权，等.频谱法在光的双缝干涉计算中的应用［J］.南京气象学院学报，2000，23（3）：445-448.

［8］李喜德，伍小平.用快速傅里叶变换实现双曝光散斑场的全场信息再现［J］.光子学报，1996，25（3）：261-265.

［9］俞晓磊，赵志敏，郭林峰.激光散斑干涉条纹的CCD分析技术研究［J］.应用激光，2007，27（5）：378-381.