亥姆霍兹旋转木马的实验研究

吕家琪,牛孔贞,李训谱

(南开大学 物理科学学院，天津 300071)

1 引 言

约150年前，亥姆霍兹(Hermann Ludwig Ferdinand von Helmholtz)为了测量声音的频率，创造了历史上第一个声音“频谱分析器”——亥姆霍兹共振器[1]，实现了对于声音频率的测定. 在其后的很长一段时间里亥姆霍兹共振器一直是放大、扩声、吸声而且不用电子技术的设备[2]. 随着理论与技术的发展，如今亥姆霍兹共振器在乐器制造、噪声控制[3]、工业技术优化[4]等方面依然发挥着重大作用. 亥姆霍兹旋转木马就是在其共振过程中产生的一个有趣的声-动能转化现象.

2 实验原理

2.1 亥姆霍兹共振器共振原理

所谓亥姆霍兹共振简言之就是空腔内的气体共振现象. 图1为亥姆霍兹共振器早期作为测定频率的装置的图片. 当向空腔口吹气时，在适当情况下会发出较大的嗡嗡声，这就是亥姆霍兹共振现象. 当在共振器的口部施加空气压力时，共振器内的气体将被压缩，假设口部气体体积不改变，只是空腔内的空气体积被压缩，由于声音的波长远大于共振器的尺寸，故可以简化成为弹簧振子模型. 此时腔内气体就相当于被压缩的弹簧，腔颈气体相当于振子，当撤去外界施压后，弹簧将弹起，而此时的腔颈内气体将向共振器外射出. 当膨胀过程到达极限时，由于分子之间的作用力，排出的气体又会回到共振器内，周而复始，便产生振动. 根据经验公式，依据环境条件和共振器的性质参量计算出共振器的共振频率为

其中Le=L+1.5r，v为声速，A为腔口横截面积，r为腔口横截面半径，L为腔颈长度，V为空腔体积[5].

图1 亥姆霍兹共振器

2.2 亥姆霍兹旋转木马的运动机理

亥姆霍兹旋转木马的基本结构是将2个相同的亥姆霍兹共振器反向对称固定于长度、重量适宜的杆的两端，并在杆的中间位置用细的针顶起或是用细绳悬挂. 当外加的声音与亥姆霍兹共振器的共振频率相同时，便会产生共振，即相当于共振器内的气体被施加以周期性外力. 根据亥姆霍兹共振器原理，当气体压缩达到极限后，气体将如弹簧产生反弹，部分气体被排出. 气体排出装置，腔内气体将变稀薄，当到达极限时，气体又会由于分子间的作用力返回到空腔内. 由于空气分子的平均间距在10-9m的量级，此时气体分子与气体分子之间、气体分子与空腔壁之间的引力很小，故在此弹簧模型中弹簧的压缩反弹过程比膨胀恢复过程提供动力的效果更明显，故可认为整个装置总体上向外排气. 根据火箭运动原理，装置将会沿着腔颈口指向腔底的方向转动.

3 实验过程

3.1 亥姆霍兹旋转木马实验装置设计

实验装置如图2所示，亥姆霍兹共振器是饮料瓶，用带底座的针头作为旋转支点，以轻质木条作为旋转臂. 声音通过外放音箱提供，实验数据通过录像之后对视频文件逐帧测量来得到.

图2 亥姆霍兹旋转木马实验装置

3.2 共振频率确定实验

以2.5 L可乐瓶为例，得到其共振频率的方法是：在饮料瓶口吹气，当听到较大的嗡嗡声即共振时，用录音笔录下产生的声音信号，并对其进行频谱分析，得到频谱图如图3所示. 在谱线上可以找到几个明显的峰值频率 ：93.75，187.50，281.20，359.30，484.30，671.80 Hz. 接下来在其他条件(响度、波形)相同的情况下，分别以这些频率为声音信号施加在亥姆霍兹旋转木马上，观察现象，看在什么频率下装置才会转动.

图3 声音频谱图

实验表明，只有频率在93.75 Hz时，装置才产生转动. 但是由于在频谱线上的取值并不很精确，于是在控制其他条件(响度、波形)不变的情况下在93.75 Hz周围每隔0.25 Hz取1个点，从93.25 Hz取到95.00 Hz，测其周围频率点的转动快慢. 当装置每转过弧度π时记录1次时间，根据时间与转过角度的关系计算角加速度进而比较快慢. 在其他条件相同的情况下，不同频率下转过的角度与时间关系的实验数据如表1所示.

根据表1做出不同频率下的θ-t曲线，并做多项式拟合. 以角加速度最大的93.75 Hz为例，θ-t

表1 不同频率下转过的角度与时间关系的实验数据

曲线见图4，θ=0.006 0t2+0.07t-2.4,R=0.998 98,发现其为拟合度很高的匀加速运动关系. 根据得出的拟合方程，可以计算出不同频率下的角加速度. 将角加速度和频率的关系做出曲线如图5所示，并与实验所用的93.75Hz的声音信号频谱图像(如图6)作对比，发现两者形态基本相同. 由此可得2.5 L可乐瓶作为亥姆霍兹共振器的实际共振频率即为单频93.75 Hz.

图4 θ-t曲线

图曲线

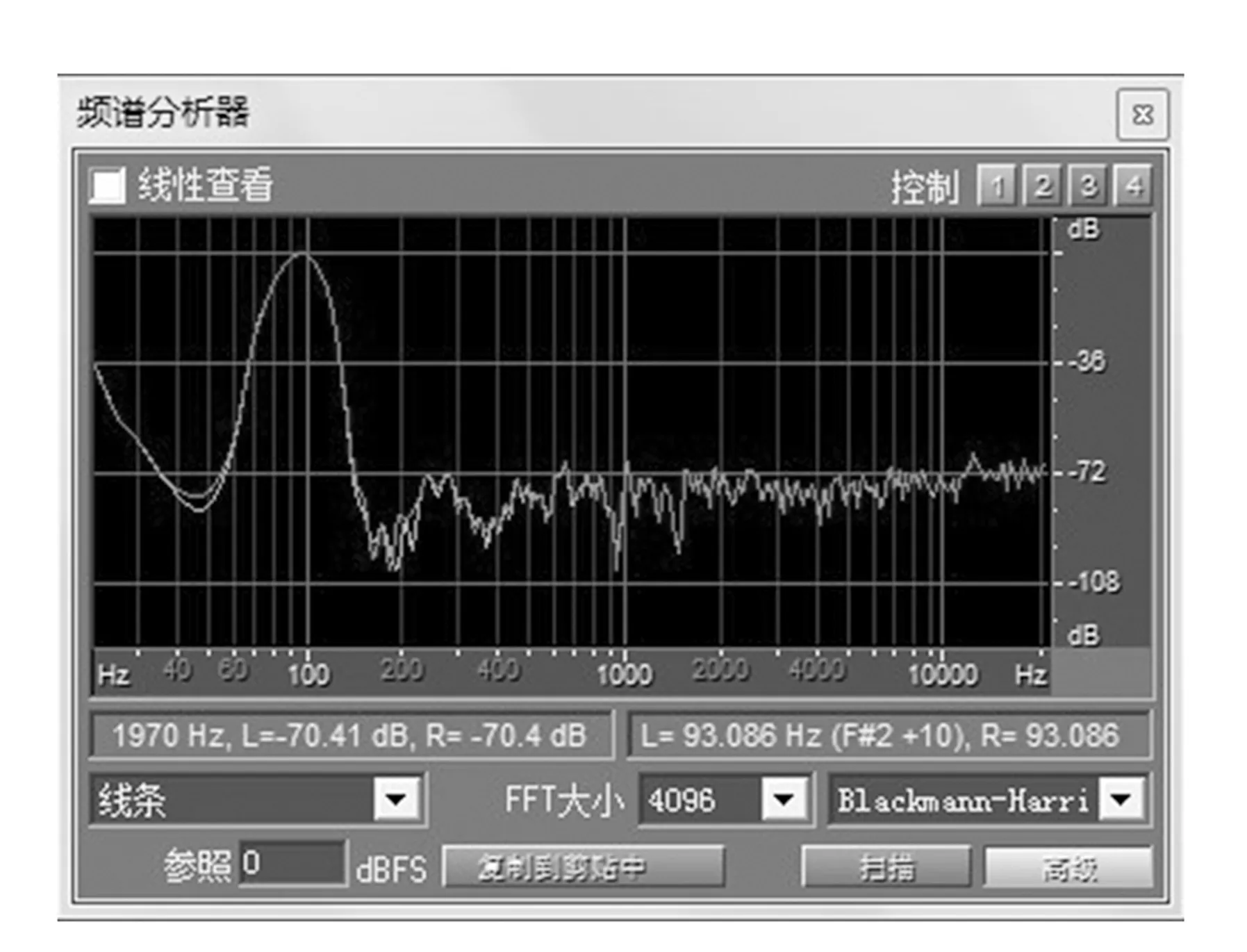
图6 93.75 Hz声音信号频谱图

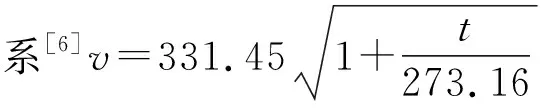
3.3 长时间运动最终状态

亥姆霍兹旋转木马的转动从能量角度来看是声波振动的能量转化为了装置的转动动能. 由于声源稳定，能量必存在上限值，装置在长时间的情况下不可能一直进行匀加速运动，而会逐渐到达稳定状态. 基于这样的考虑，把实验时间扩展到5 min(93.75 Hz，正弦波，响度固定)，并观察其现象. 结果发现装置先是加速运动(如图A段)，其后一段时间速度稳定为匀速(B段)，到120 s以后开始减速(C段)，并在169 s时停止运动. 为了与能量建立更直接的关系，取转动路程为纵坐标，运动时间为横坐标，记录数据，做出运动时间与路程关系图(L-t图)，如图7所示. 然后通过观察加速度变化分析运动过程.

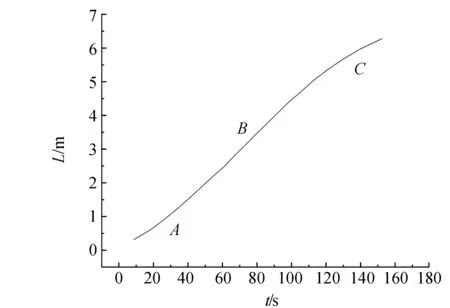
图7 L-t关系图

这一过程与理论分析相吻合：气体向外排出是主要过程，而气体吸入则是次要过程. 这也就是说气体排出的量要大于气体的吸入量，气体要不断流失，这既是装置得以运动的原因，又是装置最终会静止的原因. 由于腔内气体整体上呈排出状态，根据动量守恒定律装置将会沿远离腔口的方向运动. 同时腔内气体在运动过程中将逐渐稀薄，此时撞向瓶底获得反向速度的气体分子数也将越来越少，排气过程逐渐减弱，排气量和排气速度都不断降低，最终由于存在外界阻力，装置将变为匀速运动进而变为减速运动直至静止. 在装置运动过程中，当把手放在腔口时也能感受到3个不同阶段排出装置的气流强度逐渐减弱的变化.

3.4 波形影响实验

就不同波形对亥姆霍兹旋转木马转动角加速度的影响做了研究. 在其他条件不变的情况下改变外加声音的波形，观察并测量、计算装置转动的角加速度. 采用的波形有：正弦波、半正弦波、三角波、方波，得出了波形为方波时装置转动的角加速度明显最大的结论(数据和实验曲线从略). 这一现象可以从能量角度加以分析：由方波的傅里叶展开可知，方波在其基频上的展开系数相比其他几种波形要大[7]，也就是说声能量更大，又由于本实验装置是依靠单一共振频率驱动，所以方波对共振时的能量输入更多. 故在其他条件相同的情况下，方波信号驱动下装置转动的角加速度明显最大.

4 结束语

通过用自行设计的简易实验装置对亥姆霍兹旋转木马的声-动能转化现象进行观察、分析和讨论，加深了对这一有趣物理现象的认识和理解，进一步感受到物理世界的奥妙，激发了对物理学习的兴趣. 通过本实验所测定的共振器共振频率与用理论公式计算得到的结果基本相符，说明了用比较角加速度大小的方法研究亥姆霍兹旋转木马是一种简便可行的方法. 本实验还对旋转的全过程及波形对转动快慢的影响进行了有益探索.

参考文献：

[1] 马大猷. 亥姆霍兹共鸣器的发展[J]. 物理,1993(8):452-456.

[2] 马大猷. 亥姆霍兹共鸣器[J]. 声学技术，2002(Z1):1-3.

[3] 晏伟成，景晓东. 基于主动亥姆霍兹共振器的噪声控制实现[A]. 自动化及先进集成技术大会论文集(二)[C]，2007:333-335.

[4] 孔德鹏，李宏楷，刘云磊，等. 基于亥姆霍兹共振腔的香味自动排放装置设计[J]. 电脑知识与技术，2012(31):7589-7591.

[5] Tom Irvine. Beverage Bottles as Helmholtz Resonators. [EB/OL]. vibrationdata.com. 2004:1-13.

[6] 郭立群，吴波，黄艳芳，等. 声速随温度变化的智能测试研究实验[J]. 物理实验，2013，33(6):20-22.

[7] 刘光旭，张效成，赖学坚. 高等数学[M]. 北京:高等教育出版社，2008:308-309.