用静电计比较导体电容大小实验的分析
赵士鹏,宿丽叔,拾景忠
(江苏师范大学 a.物理与电子工程学院;b.教师教育学院,江苏 徐州 221116)
1 引 言
电容(或称电容量)是表现电容器容纳电荷本领的物理量,从物理学上讲,是一种静态电荷存储介质. 孤立导体的电容就是远离其他物体的导体的电容,一般认为:孤立导体与无穷远处构成电容,导体接地等效于接到无穷远处,并与大地连接成整体[1]. 对于2个孤立导体来说,可以借助静电计来判断电容的大小.
通过分析静电计的构造,发现静电计本身就是电容器. 其中金属球、金属杆、指针相当于电容器的一个电极板,金属外壳相当于另一个电极板,它们之间是绝缘的. 静电计的电容大小由金属外壳的大小和金属杆及指针的长短、位置所决定. 因为指针的偏转角变化对静电计的电容的影响很小,故在指针转动过程中可近似认为静电计的电容值不变[2].
根据Q=CU可知,当静电计电容保持不变时,静电计两极间的电势差U与其带电量Q成正比,U越大,Q越大,指针所受电场力越大,指针张角因此就越大. 由此可见,指针张角大小能定性地反映静电计两极间的电势差的大小.
2 电容大小的比较
对于孤立导体,它的电容取决于导体本身的形状、大小等因素,通过对导体电容和静电计原理的分析,笔者提出以下2种方法来定性地判断两导体电容的大小.
2.1 导体带电荷量Q0相同
2.1.1 实验操作
让两导体接触,通过静电感应的方法,使两导体分别带上等值异号的电荷,设电荷量大小为Q0,导体1的电容为C1,导体2的电容为C2,静电计的电容为C静,让两导体分别与静电计接触,根据静电计指针张角的大小,可以判断两导体对地电势的大小.
2.1.2 原理分析
由于导体与静电计直接相连,如图1所示,可知导体的电容C1与静电计的电容C静是并联的,根据并联电容的公式,得到C1+C静=Q0/V1(Q0也为导体和静电计接触后总的电荷量),导出
同理可得
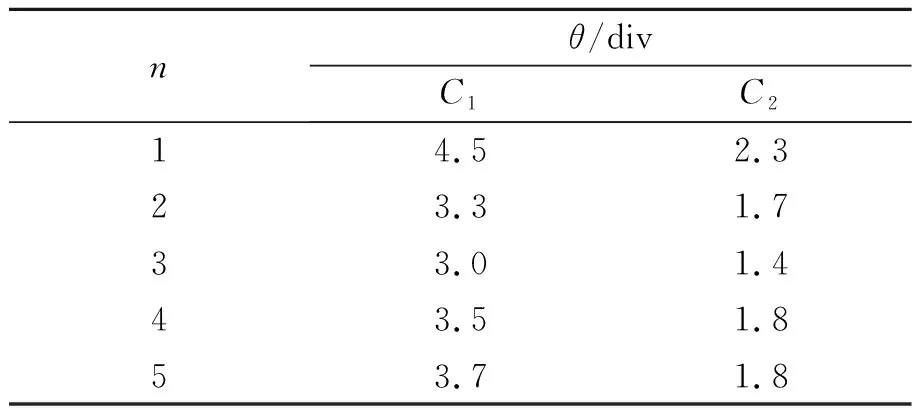
根据静电计张角的大小可以判断V1和V2的大小,若V1>V2,则根据式(1)和(2)可以得出C1 图1 原理示意图 2.1.3 实验结果 实验时选取了2个电容器,通过静电感应使2个电容带上大小相等的电荷量,与静电计链接,根据指针张角大小来判断电容的大小(每次电容与静电计接触前,应把静电计上多余的电荷中和掉). 表1是实验时通过感应得到不同电荷量的结果. 对于同一次实验,2个电容的电量大小是相等的,但对于不同次的实验,由于静电感应不同,引起每次的电荷量不相等;表中张角θ为指针张开的格数. 表1 电容带电量相同时实验数据 2.2.1 实验操作 让两导体接触,通过接触法给两导体带电,将两导体分开后,两导体对地电势相等,让两导体分别与静电计接触,根据静电计指针张角的大小,可以判断两导体对地电势的大小. 2.2.2 原理分析 设导体对地的电势为U0,可得Q1=C1U0,Q2=C2U0,根据C1+C静=Q0/V1,可得 此时,若V1 2.2.3 实验结果 同样选取上述2个电容器,通过接触法使2个电容带上相同大小的电势,与静电计链接,根据指针张角大小来判断电容的大小. 表2是实验时通过接触得到不同电势的结果,用同一电源给2个电容带相等的电势. 表2 电容带电量相同时实验数据 通过上面的分析论证,可以得到对于孤立导体,借助静电计比较它们电容的大小,这2种方法具有原理突出、操作简单、物理意义直观等优点. 但静电计作为半定量仪器,有一定的误差,如果2个电容大小相差不是很大,实验结果不是很明显. 参考文献: [1] 余建刚. 浅谈验电器与静电计的差异[J]. 教学仪器与实验,2006(1):27-28. [2] 王广云,冯如鹤. 孤立导体的电容[J]. 技术物理教学,2005(3):24-25.
2.2 对地电势U0相同

3 结束语

