方形薄板二维驻波的研究

方奕忠，王 钢，沈 韩，崔新图，廖德驹，冯饶慧

（中山大学 物理科学与工程技术学院，广东 广州510275）

1 引 言

克拉尼图形是物理演示实验中的重要课题，常被作为大学预备性物理实验的教学内容［1］，类似的振动问题也常见报道［2］.对于长方形（或正方形）薄板的克拉尼图形的研究，之前主要集中在低频段（f＜1kHz）［3］，文献上未见高频段的报道.本实验将在高频段从实验和理论两方面研究克拉尼图形，讨论振动源在方形板角落或任意点时的振动情形，并将实验值与理论解进行对比.

2 实验原理与理论模型

考虑如图1所示的二维长方形薄铜板，假定其质量分布均匀，厚度为2h（h很小），边长分别为a和b.在铜板的一角（设为原点O）有一振动点源，以某一固定圆频率ω0＝2πf垂直于铜板面作简谐振动.下面考虑其振动问题，求出共振发生时的简正模式［4］，并与实验测出的克拉尼图形比较.

图1 二维平板振动原理

假定水平放置的薄铜板的质量体密度为ρ，弹性模量为Q，由弹性力学或理论声学［5］知识可知，若设其竖直方向小振动的传播速度（相速）为u，（x，y）点处（0＜x＜a，0＜y＜b）在t时刻的振动位移（挠度）为η（x，y，t）（取静止时的位移为零），则η满足以下方程：

其中▽4＝▽2▽2，▽2为 Laplace算符，1／c2＝3ρ（1-s2）／（Qh2）.s是泊松比，对大多数材料，s约为0.25～0.33.类似参考文献［5］，为了研究板的简谐振动，令η＝Z（x，y）e-iωt，Z的微分方程可写为

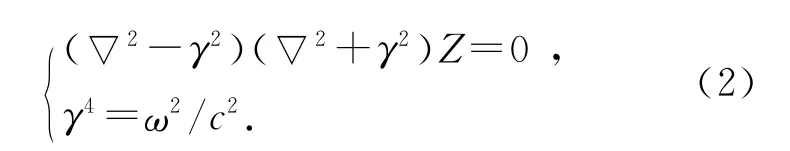
所以Z可以是方程

或

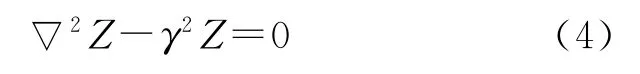
的解，通常应该是两者的线形组合，此时γ相当于简谐波的波矢k.设边界为自由边界，在薄板很薄，振动很小，板所受的重力可忽略的情况下，边界上的弯矩、扭矩及竖直方向剪力均为0，此时边条件为［6］

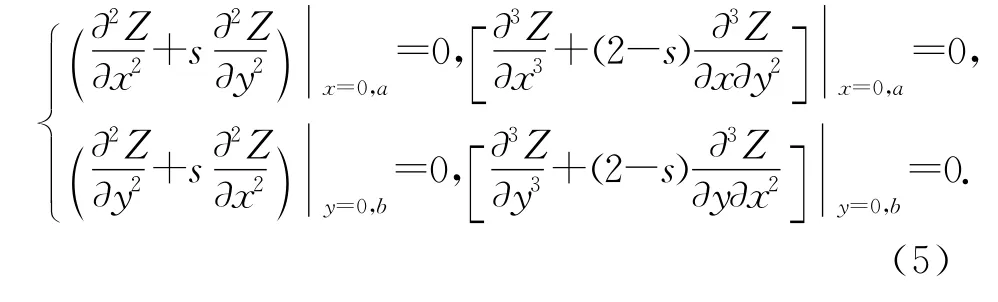
考虑无初值问题，点O（0，0）处振源满足

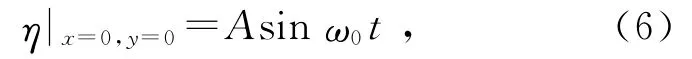
对Z分离变量，令Z＝X（x）Y（y），设式（3）的解为Z1，式（4）的解为Z2，则Z＝Z1＋Z2，其中

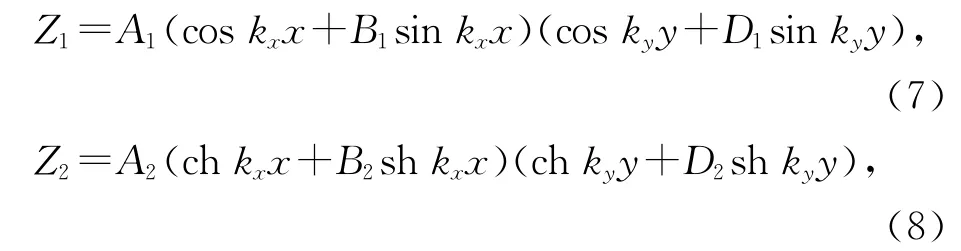
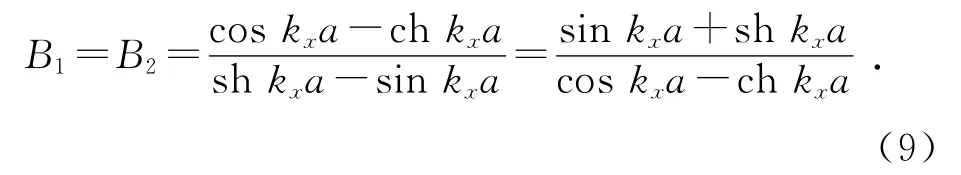
同理，D1，D2及ky也满足类似的方程，只需将式中的a改为b.先考虑kx，由（9）式得

令β＝kxa／π，把容许的β由小到大排列，有β1＝1.505 6，β2＝2.499 7，β3＝3.500 0，….由此可知，当n＞2时，βn≈n＋，有kxna＝πβn.同理，令kymb＝πβm，则当m＝n时，有βm＝βn.若令an＝cm＝，bn＝B1，dm＝，可以证明，当n＞2，m＞2时，有

其中

下面只考虑φn（x），后面可对φm（y）作类似处理.式（12）中

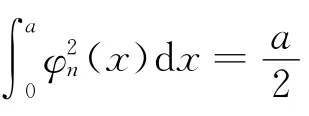
当n＞2时，有

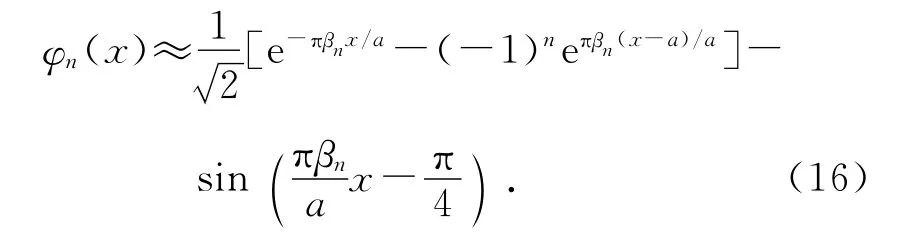
通过数值计算，如n＝2时，φ2（x）的节点为

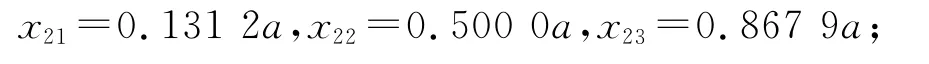
n＝3时，φ3（x）的节点为

由文献［5］知，φn（x）的节点数为n＋1，注意节点的分布关于过薄板中心点且与y轴平行的直线对称.对y方向的分析也完全类似，将式（16）中的a改为b，n改为m，x改为y，可得m＞2时，有

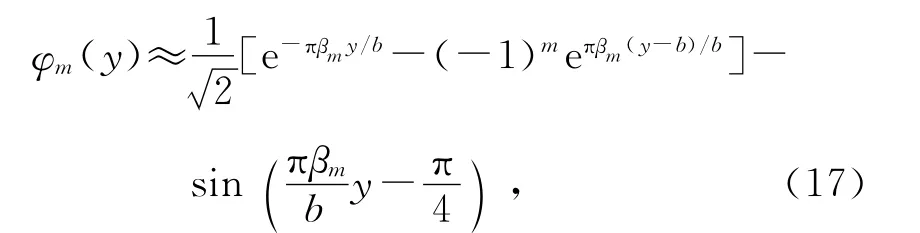
于是得到方程（1）在自由边条件（5）下的解的简正模式为

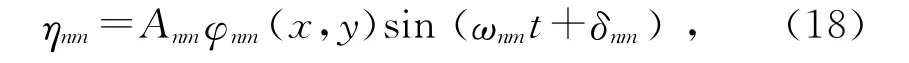
通解为（18）式的线性组合.由此可看到，当

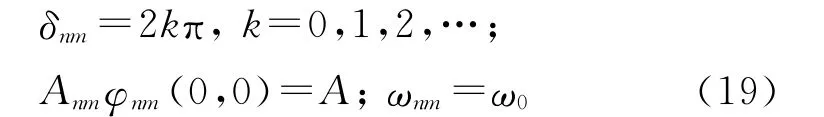
时，可得到一系列的简正振动：

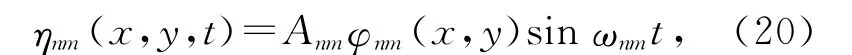
故有k＝ω0／u＝γ.此时φnm（x，y）＝0的位置就是共振驻波波节线的位置.注意

有波速

c见式（1），为常量.由式（22）知，薄板为频散媒质，波速（即相速）随频率f变化而变化.对方形板，a＝b，波速可表示为

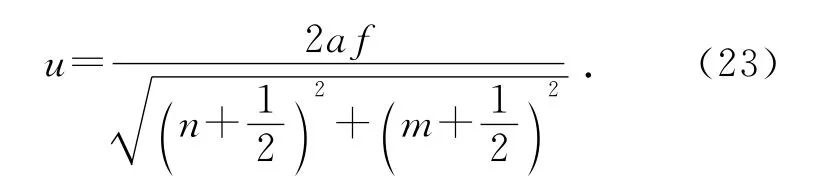
于是可在实验上分别数出x，y方向某一频率f下共振时的克尼拉图形中的波节数n＋1，m＋1，代入式（22）或式（23），即可求出波速u.

3 实验结果与分析

实验选取a＝b＝200mm，厚度2h＝1mm的黄铜板，振动源采用压电陶瓷蜂鸣片.结果如表1所示.x方向的波节数为n＋1，y方向的波节数m＋1.可见，在各种频率下，测出常量c的平均值为0.985m2／s.铜板的质量体密度ρ＝8.10×103kg／m3，注意对于黄铜，s＝0.324，由 Q＝3¯c2ρ（1-s2）／h2可求出薄铜板的弹性模量为Q＝8.44×1010kg／（m·s2）.进一步求出｜cmaxcmin｜／¯c＝0.112，可见，c比较稳定，与理论比较符合.实验上还可以与其他测量弹性模量的方法［7-8］进行比较，在此暂不讨论.

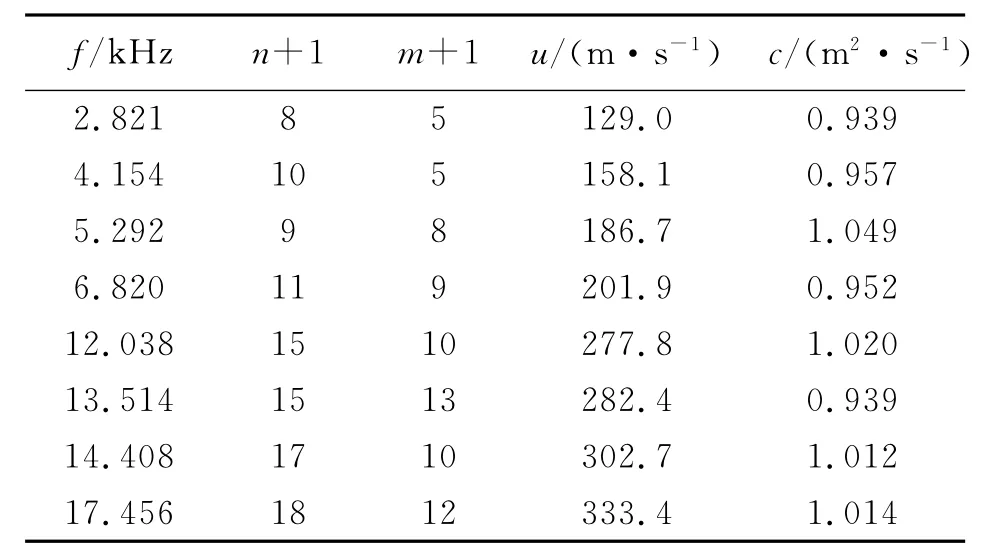
表1 xy方向波节数不同时的波速

由于铜板为正方形，a＝b＝200mm，由对称性，若仔细调节振动源的频率，可使x，y方向的波节数相等，即n＋1＝m＋1＝l＋1，式（23）可简化为

相应的实验结果如表2所示，与理论也比较符合.

表2 xy方向波节数相同时的波速

4 进一步的分析与讨论

以上是振动源在角落O（0，0）的情形.对振动源在铜板的任何位置O′（a1，b1）（0＜a1＜a，0＜b1＜b）的情形，类似前面，同样可以求解出其简正模式为：

存在振动源O′（a1，b1）时，需满足

当

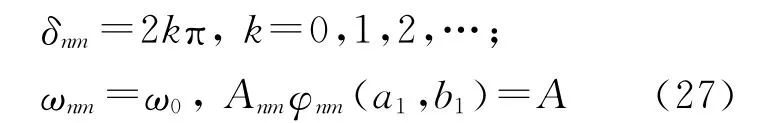
时，仍有一系列的简正振动

此时将发生共振，在xy平面上也可产生二维驻波波形，即克拉尼图形.对比式（28）和式（20）可知，不论振源在平板上的哪个位置，只要频率不变，克拉尼图形的波节（或波幅）的位置都相同，只是振幅发生改变.振幅需满足

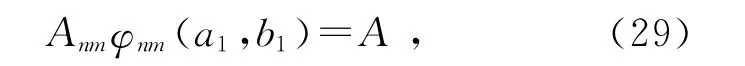
其他如波矢k、波速u等均不变.

实验观测克拉尼图形，振源难以严格放在a1＝0，b1＝0的位置，故实际上都是a1≠0，b1≠0.实验装置如图2所示，左边为有一支撑杆支撑的薄黄铜板，支撑杆靠近左下角，板上洒有白色细沙，板的底面中心附近贴有蜂鸣片，蜂鸣片通过导线与右边的DDC函数信号发生器的信号输出端相连.图3所示为实测的n＋1＝15，m＋1＝10的二维驻波图，对应频率为12.038kHz.图4为由式（20）得出的数值模拟图，两者符合得很好.其中颜色越浅表示振幅越小，颜色越深振幅越大.振幅为零代表波节的位置，即图3中细沙集中的位置.由于共振时驻波的波节位置不变，仍可应用式（18）～（23），读出x，y方向的波节数n＋1，m＋1，即可算出波矢k，从而求出波速u及弹性模量Q等物理量.

图2 实验装置图

图3 n＋1＝15，m＋1＝10时的二维驻波图

图4 n＋1＝15，m＋1＝10时的数值模拟图

［1］戴玉蓉.预备物理实验［M］.南京：东南大学出版社，2011.

［2］梁振华.声音震碎酒杯实验［J］.物理实验，2011，31（9）：16-18.

［3］王继超，王慧.Chladni图案的 Matlab模拟［J］.实验科学与技术，2011，9（2）：181-183.

［4］赵凯华，罗蔚茵.新概念物理教程·力学［M］.北京：高等教育出版社，2000：162-205.

［5］P M 莫尔斯，K U 英格特，著.理论声学（上册）［M］.吕如榆，杨训仁，译.北京：科学出版社，1984：212-218，252-253.

［6］王龙甫.弹性理论［M］.北京：科学出版社，1978：339-340.

［7］吴一，郭昶，邹永丰，等.基于叠珊条纹测量材料的弹性模量［J］.物理实验，2013，33（3）：46-48.

［8］李柱峰，徐秀平.双光栅弹性模量测量实验方法［J］.物理实验，2013，33（1）：20-22.