嵌金属丝推进剂燃烧起始阶段增速特性研究①

魏 然，鲍福廷，刘 旸

(西北工业大学 航天学院，西安 710072)



嵌金属丝推进剂燃烧起始阶段增速特性研究①

魏 然，鲍福廷，刘 旸

(西北工业大学 航天学院，西安 710072)

考虑了使用嵌金属丝装药的发动机工作过程中的多种因素，建立了金属丝与药柱、燃气间相互作用的控制方程组，并对方程组进行了数值求解，得到了嵌金属丝推进剂在燃烧起始阶段，增速比随时间的详细变化过程。结果表明，金属丝的热扩散率、熔点、直径和黑度以各自不同的方式影响金属丝的增速效果，熔点相对较低的金属丝可能会在内弹道曲线的初始阶段形成一个轻微的压强峰，固有燃速较低、着火温度较低的推进剂对嵌入金属丝较为敏感。文中数值方法计算量小，结果可靠，适于工程应用。

固体火箭发动机；药柱；嵌金属丝；燃速；数值仿真

0 引言

在固体火箭发动机推进剂中嵌入金属丝，利用金属丝远高于推进剂的导热能力提前加热推进剂，以提高药柱的整体燃速、增大推力，是广泛用于固体火箭发动机设计的手段。尤其对于需要尽量提高装填比的发动机，采用端燃嵌金属丝装药是一种较好方案。

一般而言，发动机点火之后，包埋在推进剂中的金属丝随着燃面退移而暴露于高温燃气中，金属丝在燃气中吸热、温度升高，热量传入尚未暴露的金属丝中，再向外传导，提高尚未被点燃的推进剂的初温，由此提高推进剂沿金属丝方向的燃速。燃速的增加反过来加速金属丝的暴露，增加了金属丝暴露于燃气中部分的长度，进一步增强吸热效果；另一方面，暴露于燃气中的金属丝，其温度会逐步增高直至达到熔点，最终形成“暴露-熔化”动态平衡。此时，金属丝的增速作用达到最强，并相对稳定，直至推进剂燃尽。

金属丝对推进剂燃烧的增强作用，自点火时刻起，经历了一个从几乎没有直至达到最大的连续变化过程，此过程影响了燃面退移过程。按恒定加速比计算时，金属丝附近的推进剂将形成锥形燃面；但实际情况下，由于加速比随着金属丝的暴露逐步增大，形成的燃面将略带弯曲，纵剖面呈钟形且较上述锥形燃面更浅，实际燃去的推进剂更少。这一差异直接影响到对发动机在起飞加速段的内弹道特性和推力特性的预测。

然而，对此过程细节的研究并不多，文献[1]使用多种推进剂和金属丝进行了测试，但现有实验设备无法测定沿金属丝方向燃速的实时变化，且燃速测试设备中的燃烧环境(尤其辐射传热环境)与实际发动机中的并不完全相同，也不可能用所有种类的推进剂、金属丝组合均进行实验测量，实验数据并不能直接用于发动机设计；文献[2-3]忽略了药柱内部沿轴向的导热，并对径向的导热也作了简化假设，计算结果误差较大；文献[4]就此问题建立了数值方法，可预测指定情况下嵌入金属丝的最大增速比，但未考虑推进剂性质(尤其是固有燃速)的影响，且计算是基于特定发动机进行，用于通用发动机设计仍有困难。

导弹对起飞加速段推力的要求一般是适当高一些，而嵌金属丝装药在这方面表现不佳，有时甚至需要在端面开槽来增大起飞段推力，研究这种装药在起始阶段的燃烧性质十分必要；另一方面，在涉及嵌金属丝装药的燃面退移仿真、药柱结构优化等工作中，装药在起始阶段的燃烧性质也已经成为阻碍仿真精度继续提高的瓶颈之一。为了解决这些问题，本文对嵌金属丝装药在燃烧起始阶段的增速特性进行了数学建模和数值仿真。

1 数学模型

1.1 基本假设

固体火箭发动机燃烧室是一个随推进剂燃烧不断变化的高温、高压、强热辐射环境，但其中相当一部分因素对本文所研究的问题影响甚微。为简化模型，减小数值仿真中的计算量，本文做出如下假设：

(1)金属丝与燃气间的换热方式为对流换热与辐射换热。

(2)金属丝与推进剂间的换热方式为热传导。

(3)对于不接触金属丝的推进剂，推进剂的燃烧遵循平行层燃烧规律，燃烧表面的温度为推进剂的着火温度；对于直接接触金属丝的推进剂，则在金属丝上某一段附近的推进剂温度达到推进剂着火温度时，该处推进剂被立即点燃[5]。

(4)金属丝上某段的温度达到其熔点时，由于气流冲刷作用，该段立即从金属丝上脱落，不考虑其相变吸热；在发动机内部的贫氧环境中，尚未熔化脱离金属丝主体的金属难以发生自持燃烧，且实际使用的金属丝外层往往存在保护层，故本模型不考虑金属丝被点燃和严重氧化的情况。

(5)金属丝直径较小，认为其径向上的温度没有差异，即温度梯度仅存在于长度方向上。

(6)推进剂的导热系数仅为金属丝的数千分之一。因此，仅靠近金属丝的推进剂显著地受其导热影响[6]。据仿真计算，远离金属丝10倍直径以外的推进剂，已几乎不受金属丝加热的影响，而实际发动机中，显然不可能布置密度如此之高的金属丝。因此，可忽略其他金属丝(距离较远)的影响，认为推进剂中的导热过程是以金属丝为中心的轴对称传热过程。

(7)不考虑侵蚀燃烧的影响。

1.2 控制方程

由上述假设，划分微元体见图1，金属丝只沿长度方向作一维划分，推进剂以金属丝轴心为中心划分为轴对称微元，并保持二者网格对齐。两种微元体在x方向上的长度均为dx，推进剂轴对称微元体在径向上的长度为dr。

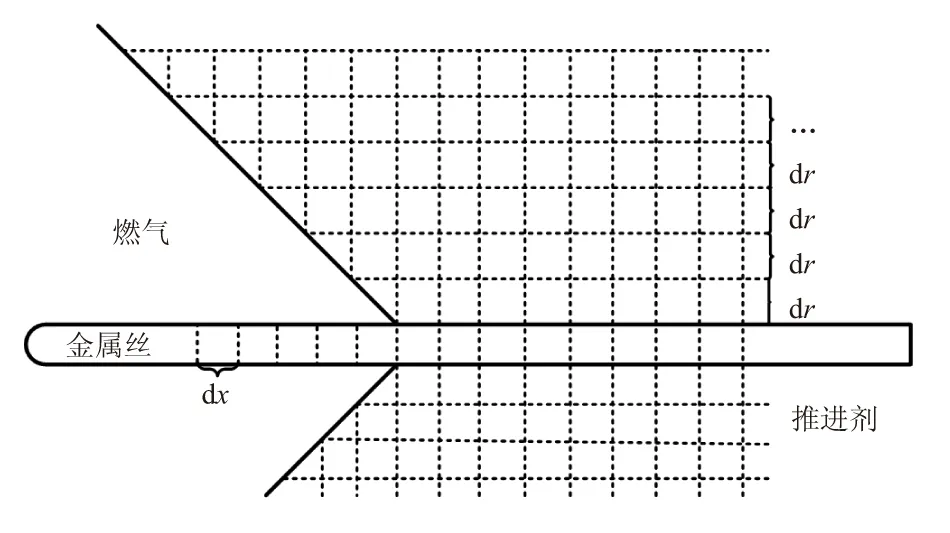
图1 微元体划分Fig.1 Schematic diagram of meshing

对于暴露在燃气中的金属丝，取图1所示的微元，则微元体横截面方向传入热量Qx为

(1)

式中 下标f表示金属丝；λf为导热系数；Tf为金属丝的温度；Af为金属丝横截面面积；dt为时间微元。

类似地，横截面方向传出热量Qx+dx：

(2)

侧向传入热量Q：

Q=qsdxdt

(3)

式中q为吸热热流密度；s为金属丝横截面周长。

侧面热交换方式为对流和辐射[5]，则有

(4)

式中h为对流换热系数；Tg为燃气温度；ε为金属丝的黑度；σ为波尔兹曼常量。

另一方面，由温升可知热容量净增为

(5)

式中ρf为金属丝密度；cf为金属丝比热容；V表示金属丝微元的体积。

则有

(6)

若令

(7)

其中，R为金属丝半径。可得到燃气侧金属丝控制方程：

(8)

对于燃气侧第一个微元体，横截面传入热量为对流换热，则式(6)中Qx应修正为Qx=qAf，将新的Qx代入式(6)，化简可得：

(9)

式中 dx为微元体在x方向上的长度。

对于埋在药柱中的金属丝，上述过程类似，仅侧面吸热变为放热，此时控制方程为

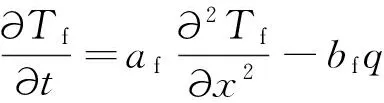
(10)

其中，q＇为金属丝向推进剂的放热热流密度：

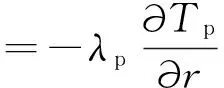
(11)

式中 各符号与上文对金属丝的推导类似；下标p表示推进剂。

可见，为求解q＇，需要知道推进剂中的温度分布。这里将推进剂视为无限大轴对称体，取微元体如图1所示，则有

dQ=Qr1-Qr2+Qx1-Qx2

(12)

式中dQ表示微元体的热容量变化；Qr1、Qr2、Qx1和Qx2分别为微元体在内外柱面、前后底面上的换热量。

代入导热基本方程与微元体几何参数，得到：

(13)

其中

(14)

即得推进剂微元体温度微分方程。

上述方程仅涉及传热现象，并未考虑推进剂的几何退移现象。事实上，在燃烧过程中，推进剂-燃气界面随燃烧逐步向发动机头部退移，而不与金属丝接触处的界面将落后于接触金属丝的部分，加之推进剂的导热系数仅为金属丝的数千分之一数量级，故远离金属丝处推进剂-燃气界面上的传热作用对上述方程所描述的传热过程几乎没有影响，忽略之则可大大简化计算量，提高计算速度。综上，本文在计算时不考虑推进剂的燃面退移。根据燃速在燃烧过程中发生的非线性变化，推进剂的燃面退移过程可使用文献[7]所述的数值方法求解，具体方法则已经超出了本文的讨论范围。

2 仿真计算

将上述方程组转换为差分方程组，使用matlab求解。求解范围设定为一根金属丝及其周围10倍金属丝直径范围内的圆柱体，初始形面为端燃推进剂内嵌1根初始暴露长度为0的金属丝。为方便描述金属丝对推进剂燃烧的促进效果，定义“增速比”Ra如下：

(15)

式中Wn为Δt时间内以固有燃速烧掉的肉厚；Wf为有金属丝情况下，Δt时间内实际沿金属丝方向燃去的肉厚。

仿真进行时，首先按照正常的燃烧过程，计算沿金属丝的燃烧与传热，同时程序持续监测因为金属丝的传热作用而点燃推进剂的事件，每次发生后，不考虑推进剂固有燃速而将燃面推进到被点燃位置，分别计算上次与本次“点燃”之间的Wn和Wf，输出当前时刻的Ra值。

为验证仿真程序的正确性，首先将仿真结果与实验数据进行了比对，使用基于文献[5]实验数据的仿真参数，具体如表1和表2所示。后文的所有仿真数据，除特别说明用于比较的因素外，其他参数均按上述数据设置。

按上述参数运行仿真程序，得到的最终增速比为5.042 9，接近文献[5]中5.3的试验实测值，可认为程序结果可信。

使用数值仿真程序，本文从金属丝物性、形态与推进剂物性3个方面，对金属丝在起始阶段的增速特性进行了研究。

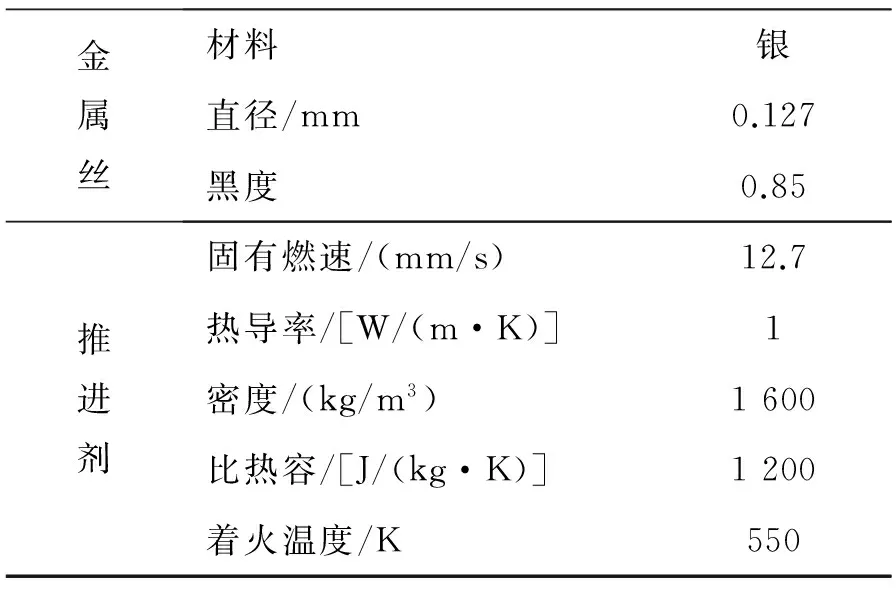
表1 仿真中使用的物性参数Table 1 Physical parameters used in simulation

表2 传热性质参数Table 2 Heat transfer properties used in simulation

2.1 金属丝物性的影响

具体来说，影响到增速特性的金属丝物性，包括导热系数、比热、密度、熔点等因素。其中，导热系数、比热、密度三者的影响可总结为热扩散率：

(16)

一般认为，热扩散率越大、熔点越高的金属丝，越能将热量有效地导入推进剂，其增速效果也就越明显。为探究两者的具体影响，采用控制变量法进行了仿真分析，计算结果与分析如下：

其中， 金属丝热扩散率对增速特性的影响与预期一致，即热扩散率越高的金属丝，其最终增速比越大，但由于热量扩散较快，难以达到热平衡，因而增速比趋于稳定所用的时间也越长，见图2。

然而， 金属丝熔点对增速特性的影响，则与上述分析略有出入。由图3可看出，其他条件不变的情况下，当熔点低于某一数值时，最终增速比随熔点的升高而增大；但熔点高于某一数值之后，最终增速比则不再随之增大。

出现这种情况的原因在于金属丝熔点之所以能够影响到其增速比，是因为高熔点的金属丝不易熔化，因而保留在燃气中的部分更长，可更有效地吸收热量。但对于远离燃面的金属丝而言，其吸收的热量实际上难以传导到推进剂中，对于加速燃烧起到的作用很小。保留在燃气中的金属丝越长，这种效应就越明显。可见，熔点对金属丝增速效果的促进作用是有上限的。

值得注意的是图3中增速比在达到最大值之后，可能会有一个轻微的下降，最终趋于稳定。这在图3中Mf=800～1 100 K的4条曲线中表现得较明显。

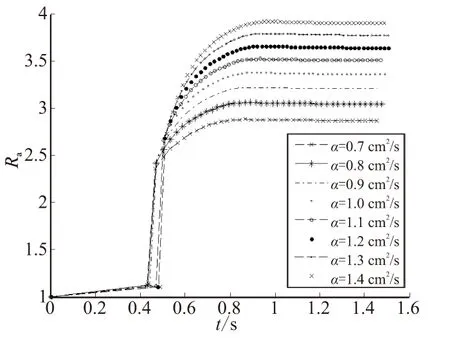
图2 金属丝热扩散率对增速特性的影响Fig.2 Effect of thermal diffusivity on acceleration rate

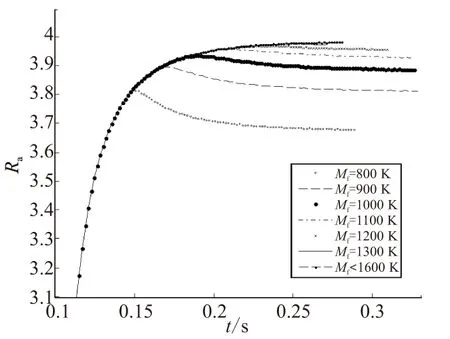
图3 金属丝熔点对增速特性的影响Fig.3 Effect of melting point on acceleration rate

出现这种现象的原因是整条金属丝的温度分布在开始时，温度较低且均匀，与稳定状态下从高到低有所区别。在2种状态的过渡中，会有一个短暂的时期，暴露燃气中的部分金属丝因为温度尚未升高到熔点，因而仍在发挥吸热作用。但当传热状态趋于稳定时，这段金属丝将被烧熔，暴露在燃气中的金属丝长度随之缩短，吸热效果下降，增速比也会略微降低。这在熔点相对较低的金属丝中表现得尤为明显。图4为仿真中800 K熔点金属丝暴露长度与增速比随时间变化的情况。图4中，Le表示暴露金属丝长度。容易看出，增速比与金属丝暴露长度的变化情况几乎同步，增速比变化略有延迟是由于热量从金属丝到推进剂的传递需要时间。图3中出现的上述2种现象，都可从暴露金属丝长度的变化中得到解释，这从侧面证明了本文仿真算法的正确性。

2.2 金属丝尺寸与黑度的影响

除了物性的影响，金属丝的外观形态，如金属丝的尺寸与表面黑度也可影响其增速特性。类似上面，固定其他条件，改变这2种因素进行仿真计算，结果见图5和图6。

图4 金属丝暴露长度对增速特性的影响Fig.4 Effect of length of exposed wire on acceleration rate

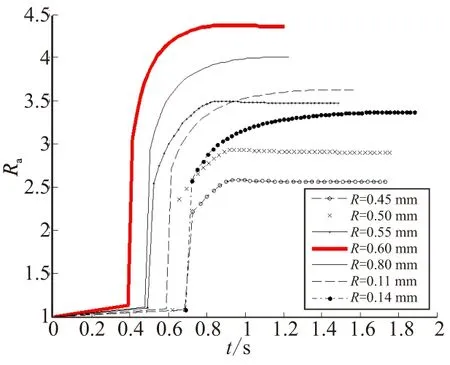
图5 金属丝半径对增速特性的影响Fig.5 Effect of fiber radius on acceleration rate

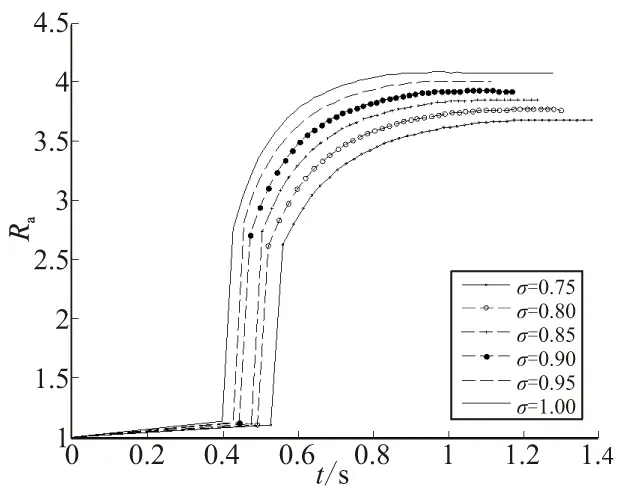
图6 金属丝黑度对增速特性的影响Fig.6 Effect of fiber blackness on acceleration rate

由图5可看出，其他条件不变的情况下，存在着一个最佳半径，使金属丝的增速比达到最大。对于银丝，这一最佳半径约是0.06 mm，这与文献[4]中算得的0.05 mm和文献[5]中的0.063 5 mm基本一致。

出现这种现象的原因有两方面：(1)小直径的金属丝，其表面积/体积比较大，在对流换热的条件下升温很快，加速其熔化，从而减小暴露于燃气中金属丝的最大长度，最终减弱增速效果；(2)较小的直径限制了其导热功率，不能将很多热量传入推进剂，难以将附近的推进剂加热到点火温度，削弱增速效果。

对于过粗的金属丝，刚好与上面相反：具有较小的表面积/体积比，因而升温较慢，且其周长更大，传入推进剂的热量将被分散到较大体积的推进剂中，同样不利于对推进剂燃烧的促进作用。

由图6则容易看出，金属黑度对增速作用的影响是单调的。这一点容易理解，黑度越高，则金属丝表面越接近于黑体，越有利于通过辐射作用吸收热量，从而增速效果越明显。

2.3 推进剂物性的影响

推进剂物性中，能够影响到增速作用的因素包括推进剂固有燃速和推进剂着火温度。二者对增速作用的影响见图7与图8。理论上，推进剂的热扩散率也可影响到增速效果，但实际上，推进剂的热扩散率仅仅是金属丝的数千分之一[8]。计算证明，其对增速比几乎没有影响，计算结果在此不再列出。

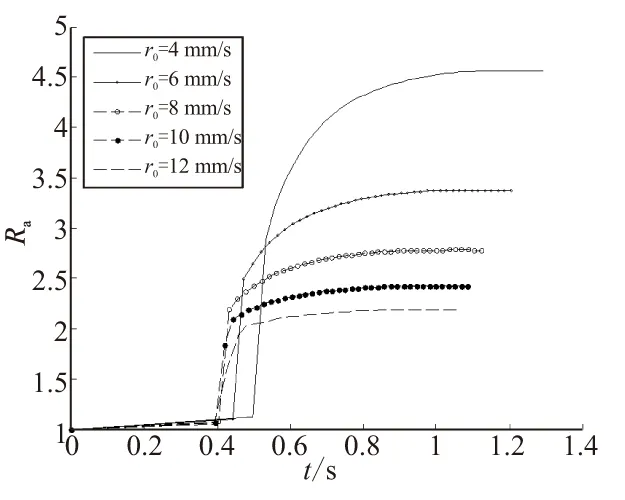
图7 推进剂固有燃速对增速特性的影响Fig.7 Effect of the inherent burning rate of propellant on acceleration rate

图8 推进剂着火温度对增速特性的影响Fig.8 Effect of the ignition temperature of propellant on acceleration rate

由图7可看出，推进剂固有燃速对增速特性有较大的影响。这一点可解释为固有燃速较大的推进剂，其本身有着较高的燃面退移速度。所以，靠近燃面处较热的金属丝会因为燃面的退移被暴露出来，从而失去了加速燃烧的作用，或者说，部分增速作用被较高的固有燃速“掩盖”了。

从这里可得出一个结论：嵌入金属丝对低燃速推进剂的增速效果明显，对于固有燃速本来就较高的推进剂，则意义不大。

由图8可知，着火温度对增速比的影响同样是单调的，着火温度越低，最大增速比越大。这一点同样容易理解：金属丝的增速作用，实质上是通过将推进剂加热到其着火温度实现的，此温度越低，增速过程就越容易实现，宏观表现就是增速比变大。

2.4 敏感性分析

上文仿真分析了金属丝热扩散率、熔点、黑度、半径、推进剂固有燃速与点火温度共计6个因素对增速比的影响。其中，每次仿真均以表1和表2中所列数据为基础，改变其中一个因素做控制变量法仿真。以每一组仿真中变量的相对值(相对于上述两表中数据)为横坐标，以相应增速比为纵坐标，作敏感性分析，见图9。

由图9可知，金属丝热扩散率、黑度、熔点三者与增速比呈现正相关。其中，增速比对熔点的敏感度较低，且熔点上升引起的增速比上升是有上限的，熔点超过某一温度后，更高的熔点对增速作用便几乎没有贡献；热扩散率与黑度的增加，均可引起增速比的显著上升，二者图线在图9中几乎重合，若以数值而论，二者敏感度相差不大。金属丝半径则存在一个最佳值，过高或过低都将引起增速比的下降。

2种与最大增速比呈现负相关的因素是推进剂的固有燃速与点火温度，若所选推进剂这2项指标相对较高，则增速作用将受到抑制。其中，增速比对固有燃速的敏感度较大，说明对于速燃推进剂，金属丝的增速将在一定程度上被“掩盖”。

图9 参数敏感性分析Fig.9 Parameter sensitivity analysis

3 结论

(1)在燃烧的最起始阶段，推进剂中嵌入的金属丝几乎没有增速效果；随后，增速比会经历一次较快的攀升，之后可能略微下降，最终达到稳定状态。

(2)金属丝热扩散率、熔点、黑度与直径均对金属丝的增速特性有影响，应根据需要对这些因素进行合理选择搭配；对于固有燃速较高的推进剂，金属丝的增速效果相对较弱。

(3)熔点相对较低的金属丝，其增速比可能在达到最高后又出现轻微下降，从而可能在点火压强峰后形成另一个压强峰，设计时应予注意。

[1] 张炜，朱慧，夏智勋，等. 嵌银丝贫氧推进剂燃烧特性[J].国防科技大学学报，2011,23(6): 17-19.

[2] Merrill K King. Analytical modeling of effects of wires on solid motor ballistics[J]. Journal of Propulsion and Power,1991,7(3): 312-321.

[3] 童明生，张弘. 导弹燃烧室内火药埋置金属丝燃速的模拟计算和程序设计[J]. 计算机工程与设计，1998,19(3): 6-11,21.

[4] 张有为，王晓宏，杨举贤. 嵌金属丝端燃药柱燃烧过程的数值研究[J]. 推进技术，2007,28(2): 4-8.

[5] 李宜敏，张中钦，张远君，等. 固体火箭发动机原理(第一版)[M]. 西安：西北工业大学出版社，1991.

[6] Kubota N，Ichida H. 嵌金属丝推进剂的燃烧过程[J]. AIAA Journal,1983,20(1): 116-121.

[7] 刘旸,鲍福廷，蔡强，等. 基于 GPU 计算架构的体素离散化复杂药柱燃面计算方法[J]. 固体火箭技术，2011，34(1): 18-22.

[8] 赵威，张领科. 复合底排推进剂点火燃烧特性研究[D]. 南京理工大学,2012.

(编辑：崔贤彬)

Acceleration effect on initial stage of burning rate of grain with embedded metal wires

WEI Ran,BAO Fu-ting,LIU Yang

(College of Astronautics,Northwestern Polytechnical University,Xi'an 710072,China)

The paper takes a variety of factors during the functioning period of a solid rocket motor that uses grain with embedded wire into consideration in the establishment of a system of equations that describes the governing equations for the metal wire,the rocket grain and the gas. The equations were solved numerically to obtain the detailed change of the embedded wire over time during the initial stage of propellant combustion,and the acceleration stage. The results indicate that properties such as thermal diffusivity,melting point,diameter and blackness of the wire all affect the acceleration effect of the wire differently. Metals with relatively low melting point may produce a slight pressure peak during the initial formation of the internal ballistic curve. Previous research has shown that the propellants with slow burning rate and relatively low ignition temperature are more sensitive to the embedded wire. The calculations of the presented numerical method are simple,reliable,and suitable for engineering applications.

solid rocket motor;grain;embedded metal wires;burning rate;numerical simulation

2013-12-25；

：2014-08-02。

国家自然科学基金(51005179)。

魏然(1991—)，男，硕士生，研究方向为发动机总体设计。E-mail:wdyqq@126.com

V435

A

1006-2793(2015)01-0055-06

10.7673/j.issn.1006-2793.2015.01.010