有界控制导弹随机最优制导律①
花文华,孟庆龄,张金鹏,2
(1.中国空空导弹研究院,洛阳 471009;2.航空制导武器航空科技重点实验室,洛阳 471009)
有界控制导弹随机最优制导律①
花文华1,孟庆龄1,张金鹏1,2
(1.中国空空导弹研究院,洛阳 471009;2.航空制导武器航空科技重点实验室,洛阳 471009)
为削弱加速度界和系统噪声对拦截导弹性能的影响,基于随机控制理论,设计了一种考虑有界控制的随机最优制导律(stochastic optimal guidance law,SOGL)。通过系统降阶与性能指标变换和随机输入描述函数近似,将拦截导弹的控制有界和状态估计误差考虑到了该制导律的设计当中。同时,为削弱目标加速度估计延迟的影响,提出了一种SOGL的补偿形式,并基于Monte Carlo方法进行了仿真验证。结果表明,SOGL相比于传统的最优制导律性能得到了明显改善,而其补偿形式削弱了滤波器估计延迟的影响,更适用于目标机动存在切变的情形。
制导律;随机控制;有界控制;目标拦截
0 引言
有界控制是导弹制导系统设计中需要加以考虑的重要内容。基于线性二次型性能指标的制导方法,由于目标机动和量测噪声的影响,在制导末端往往要求较强的机动性能,如果不加以有效控制将直接影响最终的制导精度。传统的制导律和估计器设计方法大多基于确定性等价原理[1],二者分别针对完全信息情形和非完全信息情形独立优化,而在实际执行中,为考虑有界控制,直接将由估计状态所构建的控制命令加以饱和约束,所得到的最终结果并不是最优的。文献[2]正是采用了这一设计思路给出了一种有界控制制导律。文献[3-4]基于广义分离原理,将估计结果的概率密度函数考虑到制导律的设计当中,分别针对非线性和近似线性拦截情形,设计了相应的饱和最优制导律,但是该类型制导律包含较为复杂的数学计算,特别是涉及到末端状态已知的时变Riccati微分方程组的求解,工程上较难实现。
本文考虑拦截导弹具有有界控制的非完全信息情形,通过适当的系统模型和性能指标转换,设计一种有界控制随机最优制导律,并不涉及到复杂的数学计算问题,更易于实际执行,同时考虑滤波器估计延迟的影响,给出一种改进形式。
1 问题描述及建模
1.1 弹目相对运动关系数学描述
制导末端拦截导弹和目标的相对运动关系如图1所示。图中,X轴沿初始视线方向;下标m和t分别表示二者的相关状态;q为视线角;r表示拦截导弹和目标之间的相对距离;二者相对于初始视线方向的位移为y。

图1 平面相对运动关系Fig.1 Planer engagement geometry
基于下述假设进行问题的研究:
(1)拦截导弹和目标可视为质点,并可沿初始视线方向实现近似线性化;
(2)二者速度大小不变,近似具有一阶控制系统或自动驾驶仪动态;
(3)拦截导弹可对相对运动关系和自身的相关状态进行噪声下的量测,目标无法获取导弹的相关信息,但可意识到拦截企图,从而随机规避机动。
考虑拦截导弹的有控制性并基于上述假设条件,选取状态变量为x=[yvatam]T,则系统状态方程可以近似表示为
(1)
其中
式中ωm、ωt为相互独立的零均值高斯白噪声;σm、σt分别为标准方差;τm、τt分别为拦截导弹和目标的控制系统时间常数;amc、atc为相应的控制命令;sat()表示饱和函数。
基于假设(1)和假设(2),拦截导弹飞行时间为
tf=r0/Vc
(2)
式中r0为弹目初始距离;Vc为接近速度,近似为(Vm+Vt)。
剩余飞行时间可表示为
tgo=tf-t
(3)
1.2 量测方程
结合图1,采用一定的弹上设备,如导引头可对相对距离r、视线角q进行量测。假设r是可精确量测的,q具有一定的量测噪声,并且假设噪声为白噪声且符合高斯分布,标准方差为σq,则量测方程可表示为
z=Hx+vq
(4)
式中H=[1/r0 0 ];vq为量测噪声。
2 估计器和制导律设计
2.1 系统降阶
定义线性二次型性能指标:
(5)
式中G=diag(g,0,0,0);g为加权系数,一定程度上体现了导弹拦截性能和机动性能之间的折中。
基于式(1)所示的随机状态方程和性能指标(5)推导拦截导弹制导律,必然会涉及到终端条件已知的Riccati方程组求解,为避免这一过程,本文采用了系统降阶变换的设计方法。文献[5]提出了一种称为终端投影变换的系统降阶方法,采用零效脱靶量Z作为新的状态变量,以降低系统的维度。结合式(1),可求得
(6)
其中
θm=tgo/τm
θt=tgo/τt
ψ(k)=exp(-k)+k-1
将式(6)两边对t求导:
(7)
系统被降阶为以零效脱靶量作为状态变量的形式,当t=tf时,由式(6)可得到Z(tf)=y(tf),因此性能指标可进一步转化为
(8)
这一降阶过程并不涉及到近似变换,可适用于拦截导弹存在饱和非线性控制特性的情形,下文还将进行进一步的转换。
2.2 估计器设计
根据广义分离原理,估计器可独立于控制器进行设计。降阶后的系统以零效脱靶量作为状态变量,估计器需要对这一状态实现估计,因此结合系统(1)和量测方程(4),Kalman滤波器的状态变量进一步定义为z=[Z(t)vatamatc]T,则状态方程可以表示为
(9)
其中
本文主要应用成型滤波器[6]方法表示目标的随机机动策略,采用随机输入驱动系统,wtc是标准方差为σtc的白噪声过程。相应的量测方程转化为
y=Hzz+vq
(10)
其中
(11)
则Kalman滤波方程可表示为
(12)

E(η(t)η(τ))=Rδ(t-τ)
(13)
式中δ(t-τ)是Dirac函数。
Kalman滤波增益为
(14)
其中,P满足以下Riccati微分方程:
(15)
式中Q为过程噪声协方差阵;P(0)=E(z(0)zT(0))。
2.3 随机最优制导律推导
性能指标(8)可进一步表示为
(16)

(17)
结合式(12),sat(amc)通过Kalman方程只对估计值产生作用,与估计误差无关,因此制导律的设计只需要对性能指标JZ进行优化。
将式(12)展开,可得
(18)
(19)
式中K1和K5分别对应K的第1和第5个元素。
虽然进行了一定的转换,式(17)和式(18)所表示的非线性优化问题,仍无法通过一般的方法进行求解。为便于问题的求解,给出一个假设条件。
比例导引、扩展比例导引及最优制导律等典型制导方法在表达形式上可归结为一种统一的形式:
(20)
式中N为导航增益。
本文假设最终所得到的制导律具有如式(20)所示的典型形式,问题进一步转化为导航增益的设计问题,以降低求解的复杂性。参考文献[4,7],并采用随即输入描述函数(random input description function, RIDF)近似饱和函数,则式(18)可进一步表示为
(21)
其中
(22)

基于上述假设和近似,由式(17)可得
(23)
(24)
(25)
制导律的设计最终转化为状态方程式(24)约束下针对性能指标式(23)的优化问题。由此,构造Hamiltonian函数,可以得到:
(26)
式中λ为Lagrange乘子。
由于N表示导航增益且相对于H是二次的,因此可求得N的最小值为
(27)
进一步由协态方程和横截条件可得
(28)
代入式(27),可求得制导增益为
(29)
从而,所设计的随机最优制导律(stochastic optimal guidance law,SOGL)可表示为
(30)
该制导律通过系统降阶和性能指标变换,考虑到了导弹的有界控制性和状态估计误差的影响。
2.4 制导律的进一步改进
由上节的推导过程可看出,状态估计误差的概率密度函数已经被间接考虑到制导律的优化过程当中,可改善制导精度。但是,估计器的引入会带来一个明显的问题就是估计延迟,因此为进一步改进导弹的拦截性能,应要求估计误差方差和估计延迟同时的最小化,但这2种要求是存在矛盾的。一种可行的制导方案是将估计延迟因素也考虑到制导律的设计当中,采用补偿或者自适应带宽等方式,实现估计器估计误差方差和估计延迟的设计折中,从而改进拦截性能。
目标加速度估计延迟对拦截性能的影响最为明显,本文给出一种针对目标加速度估计值的直接补偿方法。将由估计延迟产生的目标加速度可达集(不确定集)的中心值代替目标加速度估计值,下面给出具体的推导过程。
由式(1)可得
at(t)=exp(-δ/τt)at(t-δ)+
(31)

(32)
(33)
因此,对于具有延迟的目标加速度有
[at(t)]min≤at(t)≤[at(t)]max
(34)
将at(t)采用由延迟产生的不确定集的中心值代替:
at(t)=([at(t)]min+[at(t)]max)/2
=at(t-δ)exp(-δ/τE)
(35)
因此,零效脱靶量可进一步修正为
(36)
其中,δ对应假设的目标加速度估计延迟。采用这一零效脱靶量表达形式用于SOGL的相关计算。改进后的形式采用CSOGL (Compensated SOGL)表示。由式(36)可得
3 仿真结果及分析
主要针对一类迎面末端拦截情形进行了仿真研究,如图1所示,γm(0)≈0,γt(0)≈0,其他仿真参数如表1所示,其中T为采样时间。针对2种形式的目标机动进行了制导律SOGL和CSOGL的验证和比较。仿真基于Monte Carlo法,并采用单发命中概率[8](single shot kill probability, SSKP)作为目标拦截性能的衡量指标。

表1 仿真参数Table 1 Simulation parameters
(1)“bang-bang”目标机动
具有随机时间切换的“bang-bang”机动被认为是最优的规避机动形式[9-10]。假设目标机动命令切换时间为tsw,图2为tsw=1.5 s情形下的目标加速度估计,当估计器具有足够的收敛时间时,可实现目标加速的较好估计。图3(a)和图3(b)分别为该情形下相应于制导律SOGL的导航增益变化曲线和脱靶量曲线,可以看出,由于受到目标机动和量测噪声的影响,导航增益峰值Nmax出现在制导末端,要求导弹具有较强的机动性能,最终的脱靶量为0.580 7 m,具有较高的制导精度。

图2 目标加速度闭环估计,“bang-bang”机动Fig.2 Close-loop estimation of target acceleration, bang-bang maneuver

(a)导航增益,SOGL

(b)脱靶量,SOGL
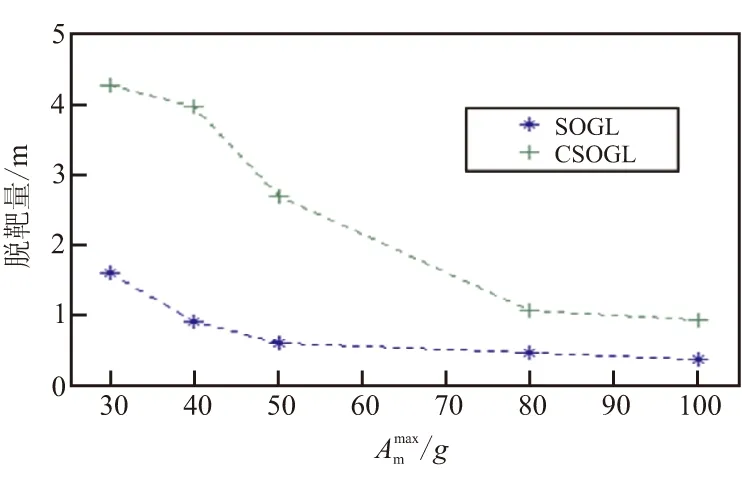
(a)脱靶量

(b)导航增益峰值,SOGL
图5给出了在“bang-bang”目标机动情形下,SOGL和CSOGL的累积脱靶量分布情况,仿真中,两者取相同的目标机动命令切换时间和随机数产生器种子。可以看出,对于给定的SSKP,例如SSKP=0.95,采用制导律CSOGL 所要求的弹头杀伤半径小于SOGL,总体而言具有较好的拦截性能。
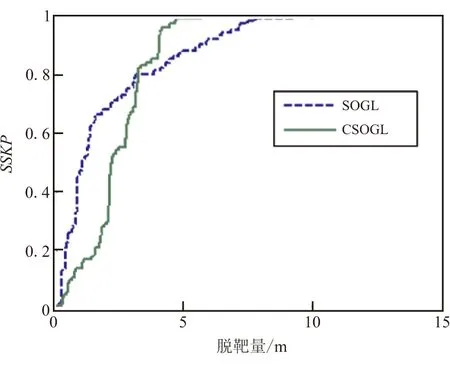
图5 累积脱靶量分布:SOGL和CSOGLFig.5 Cumulative miss distance distribution: SOGL and CSOGL
(2)常值目标机动
最优制导律(optimal guidance law,OGL)的推导基于目标常值机动的假设,为进一步验证所设计的制导律的性能,假设目标做常值机动。图6对3种制导律——OGL、SOGL和CSOGL的拦截性能进行了比较,所设计的有界控制随机最优制导律SOGL相比于OGL具有明显的性能优势,而CSOGL的性能则较差,更适用于目标机动命令存在切变而造成估计延迟的情形。
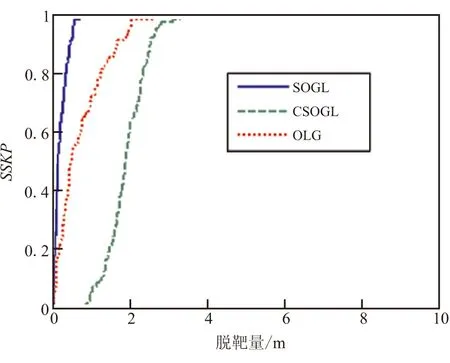
图6 累积脱靶量分布:OGL、SOGL和CSOGLFig.6 Cumulative miss distance distribution: OGL,SOGL and CSOGL
4 结论
(1)SOGL将拦截导弹的有界控制性和状态估计误差直接考虑到制导律的设计当中,为避免指令饱和,实现了弹道的及时调整,并削弱了滤波器估计误差的影响,制导性能优于最优制导律。
(2)CSOGL在SOGL的基础上进一步考虑了滤波器估计目标加速度延迟的影响,通过制导律的改进设计,估计延迟的影响被有效削弱,因此更适用于目标机动存在切变的情形,该情形下的整体性能会优于SOGL。
(3)SOGL和CSOGL在实现上并不涉及到复杂的数学计算,可适用于工程应用。
[1] Shinar J,Shima T.Nonorthodox guidance law development approach for intercepting maneuvering targets[J].Journal of Guidance,Control and Dynamics,2002,25(4):658-666.
[2] 花文华,陈兴林.变速导弹有界控制非线性微分对策制导律 [J].控制与决策,2011,26(12):1886-1890.
[3] Hexner G,Shima T.Stochastic optimal control guidance law with bounded acceleration [J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(1):71-78.
[4] Hexner G,Shima T,Weiss H.LQG guidance law with bounded acceleration command [J].IEEE Transactions on Aerospace and Electronic Systems,2008,44(1):77-86.
[5] Bryson E A,Ho C Y.Applied optimal control [M].Waltham,America:Blaisdell,1969:154-155.
[6] Zarchan P.Representation of realistic evasive maneuvers by the use of shaping filters [J].Journal of Guidance and Control,1979,2(1):290-295.
[7] Gökcek C,Kabamba P T,Meerkov S M.Disturbance rejection in control systems with saturating actuators [J].Nonlinear Analysis,2000,40(1-8):213-226.
[8] 花文华,陈兴林,宋申民.基于多模型自适应估计的混合策略微分对策制导[J].宇航学报,2010,32(6):1582-1588.
[9] Shinar J,Steinberg D.Analysis of optimal evasive maneuvers based on a linearized two-dimensional kinematic model [J].Journal of Aircraft,1977,14(8):795-802.
[10] Shinar J,Turetsky V,Oshman Y.Integrated estimation/ guidance design approach for improved homing against randomly maneuvering targets [J].Journal of Guidance,Control,and Dynamics,2007,30(1):154-161.
(编辑:吕耀辉)
Stochastic optimal guidance law for bounded-control missiles
HUA Wen-hua1,MENG Qing-ling1,ZHANG Jin-peng1,2
(1.China Airborne Missile Academy,Luoyang 471009,China;2.Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons,Luoyang 471009,China)
Based on stochastic control theory,a stochastic optimal guidance law(SOGL)considering bounded control was presented to weaken the effects of acceleration boundary and system noise of interception missiles.The control boundary and states estimation error were brought into design of the guidance law by use of system order reduction,performance index transformation and random-input description function approximation.To further reduce the effect of estimation delay,a compensated SOGL was proposed.Based on Monte Carlo method,simulations were carried out.As compared to traditional optimal guidance law,the simulation results show that the interception performance of SOGL is improved and the compensated SOGL weakens the effects of estimation delay of filter and is more suitable for target with switching maneuver.
guidance law;stochastic control;bounded control;target interception
2013-11-28;
:2014-02-24。
航空科学基金重点项目(20110112001)。
花文华(1983—),男,博士,主要研究方向为飞行器制导与控制。E-mail:huawh6611@163.com
V448
A
1006-2793(2015)01-0007-05
10.7673/j.issn.1006-2793.2015.01.002

