基于熵权和归一化样本的输电网规划方案灰色模糊综合决策方法

于慧莉，李勤新，丛颖，宫春明

(1.东北电力大学 电气工程学院,吉林 吉林 132012； 2.中国电力科学研究院，北京 100085； 3.吉林省长春供电公司，长春 130021)

0 引言

输电网规划的基本原则是在保证电能安全、可靠地输送到负荷中心的前提下，使电网的建设和运行费用最小[1]。电网规划方案的合理性、安全性、经济性和适应性将会对电力市场的发展和电力系统的安全运行产生全面而长远的影响，科学合理的电力系统规划结果，不仅可以产生巨大的社会效益，更可以创造可观的经济效益[2]。所以，对输电网规划建模和规划方案决策分析进行深入的研究，具有重要意义。

近年来，一些专家学者提出了一些评价方法对输电网规划进行经济性评价[3-4]、安全性评价[5-6]、输电能力评价[7]等，主要侧重于在单一方面对规划方案进行评价；文献[8-15]提出采用层次分析法和模糊评价法及其改进方法的输电网规划方案综合评价方法，但层次分析法和模糊评价法本身具有一定局限性，用于输电规划方案评价方法与理论还不够完善。

灰色模糊评价是一种用于已知信息量不足且对象具有模糊因素的评价方法。其中，“灰色”是“量”的概念，指信息量不充分；“模糊”是“质”的范畴，指信息中具有不明确性。输电网规划方案决策问题中经常不具备完全充分的资料且存在模糊因素，既存在灰色性又具有模糊性，即灰色模糊综合评判问题。本文将熵权法、指标归一化、灰色理论和模糊理论相结合，提出一种基于熵权和归一化样本的输电网规划方案灰色模糊综合决策方法。使用熵权法客观地计算各个指标对输电网规划方案优劣的影响权重，之后采用极差法进行归一化并模拟专家评分以获得评价样本矩阵，进而根据灰色模糊评估理论得到每个规划方案所属的模糊灰类等级而进行决策。最后通过仿真评估，证明本文提出方法的可行性。

1 规划方案灰色模糊决策分析模型

1.1 熵权法确定电网建设项目风险评价指标的权重

熵权法是一种客观赋权方法，其基本原理是根据各指标的变异程度，利用信息熵计算出各指标的熵权，结合指标的重要性和提供的信息量来确定其最终权重。

现有m个待评方案，n个评价指标，建立综合评价指标体系，形成原始方案指标矩阵

式中：vji为第i个方案的第j个指标值。

指标权重的求解过程如下：

(1)计算第j个指标在方案i中所占比重

(1)

(2)计算第j个指标的熵值

(2)

(3)计算第j个指标的熵权

(3)

最后得到各个评价指标对于规划目标的权重向量

ω=(ω1ω2ω3…ωn) 。

(4)

ωj越大，说明指标j对规划目标的影响程度越大。

1.2 构建评价样本矩阵

现有的模糊评价法和层次分析法对方案进行决策时，都依赖专家对指标评分以确定样本矩阵，人为性高且实时性差。所以，本文采用一种模拟专家评分的方法来获得评价样本矩阵。由于同一领域的不同专家对同一指标的认可度近似，因此，对评价指标进行合理的归一化处理作为专家对该指标的基础认可度，然后在此基础上进行摄动，以模拟不同专家对同一指标在评分上的细微差别，避免大规模样本带来的大量人工操作。

1.2.1 归一化处理

采用极差法对方案指标vji进行无量纲归一化处理，按指标值由优至劣依次赋予9至1之间的数值，获得无量纲归一化后的方案指标矩阵。赋值规则如图1所示。

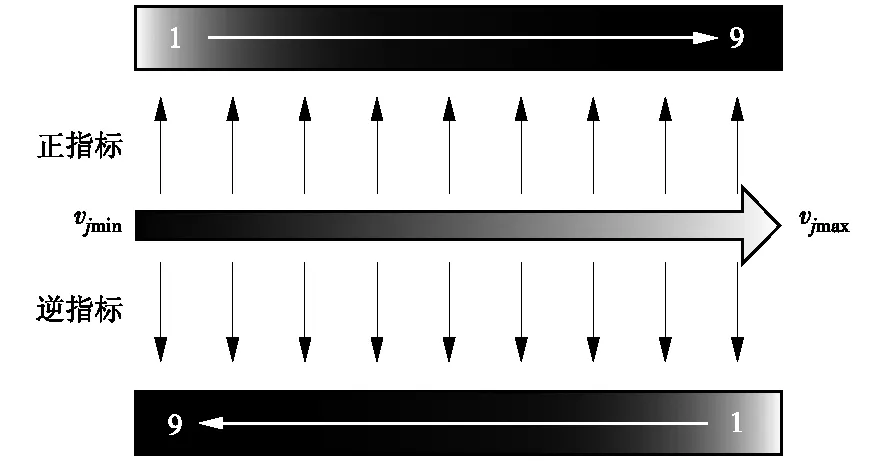
图1 归一化赋值规则

将各个指标分别按其值从小到大进行排列，指标j在各个方案中的最小值和最大值分别为vjmin和vjmax。若指标越大越好(正指标)，vjmax赋值为9，vjmin赋值为1；反之(逆指标)vjmax赋值为1，vjmin赋值为9。之后将介于vjmin和vjmax之间的指标值按比例对应于1～9之间的数值。

正指标

(5)

逆指标

(6)

式(5)、式(6)将传统极差法[16]进行改进，对原始方案指标矩阵进行无量纲归一化处理，既消除了分析时量纲和数量级带来的影响又能体现指标值的优劣。最终得到归一化后的方案指标矩阵

矩阵A中第i列(a1ia2i…ani)T即为归一化后方案i的指标向量。

1.2.2 模拟专家评价样本矩阵

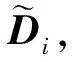
矩阵Di即为模拟的专家评价样本矩阵。

1.3 确定评价模糊灰类

确定评价模糊灰类就是规定模糊灰类的等级数、灰类的灰数以及灰数的白化权函数[17]。根据灰数d1，d2的不同，对应不同的白化权函数，常用的白化权函数有以下3种类型[18]。

(1)类型1：灰数为⊗∈[0,d1,∞)，白化权函数为

(2)类型2：灰数为⊗∈[0,d1,2d1]，白化权函数为

(3)类型3：灰数为⊗∈[0,d1,d2]，白化权函数为

1.4 计算灰色评价系数

将方案i的评价样本矩阵Di中的数据代入白化权函数，求得指标j对于第N(N=1，2，…，h)个模糊灰类的评价系数

(7)

指标j对于第N个模糊灰类的评价权重

(8)

从而得到指标j的评价权向量rj为

rj=(rj1rj2…rjN) 。

(9)

将n个指标的评价权向量综合后，得到方案i的灰色模糊评价权矩阵

1.5 评价结果

方案i的灰色模糊评价结果

Bi=ωRi=(bi1bi2…biN) 。

(10)

Bi中元素即代表各模糊灰类属于方案i的权重系数。由于人们对方案的评价并不是绝对地肯定或否定，因此综合评价结果是一个模糊集，可以按最大隶属度原则[19]或给方案打分的方法获得被评价方案所属的模糊灰类等级。

2 仿真算例

采用本文提出的方法对输电网规划研究中广泛使用的经典算例18节点系统中5个备选方案如图2所示进行综合决策，图2中实线代表已建线路、虚线代表新建线路。

根据输电网的运行特点，结合规划方案的经济性、可靠性、安全性、可开发性等方面建立综合评价指标体系，其中包括建设费用、年运行费用、风险费用、期望缺供电量(EENS)、负荷削减概率(PLC)、新建线路走廊占地、可扩展性和允许过负荷程度。规划方案评价指标体系见表1。

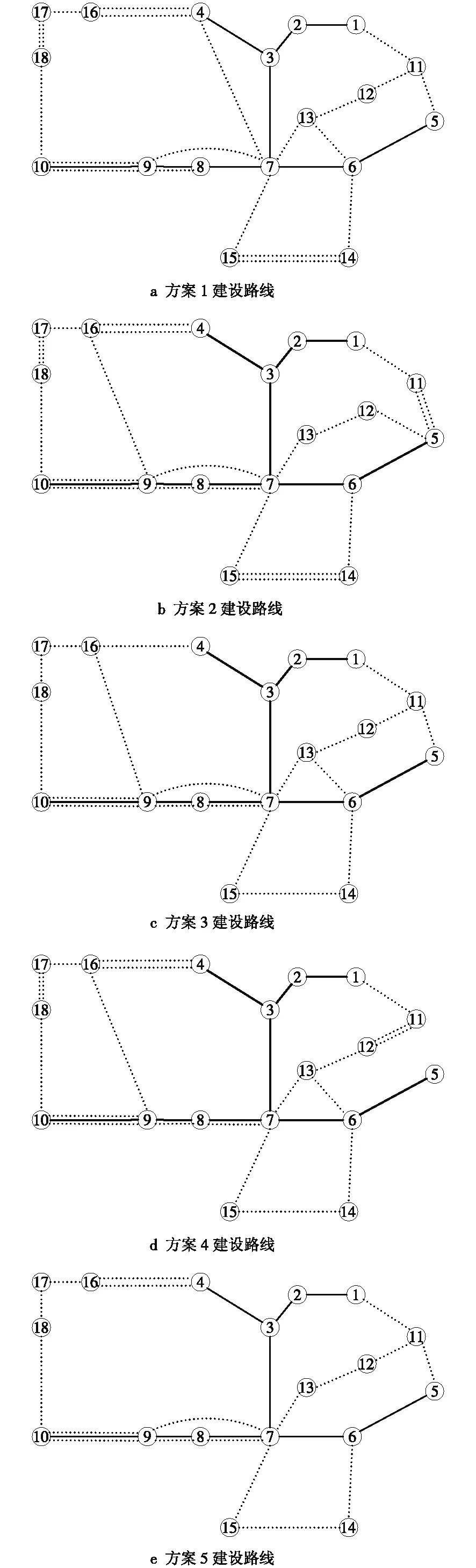
图2 18节点系统中5个备选方案

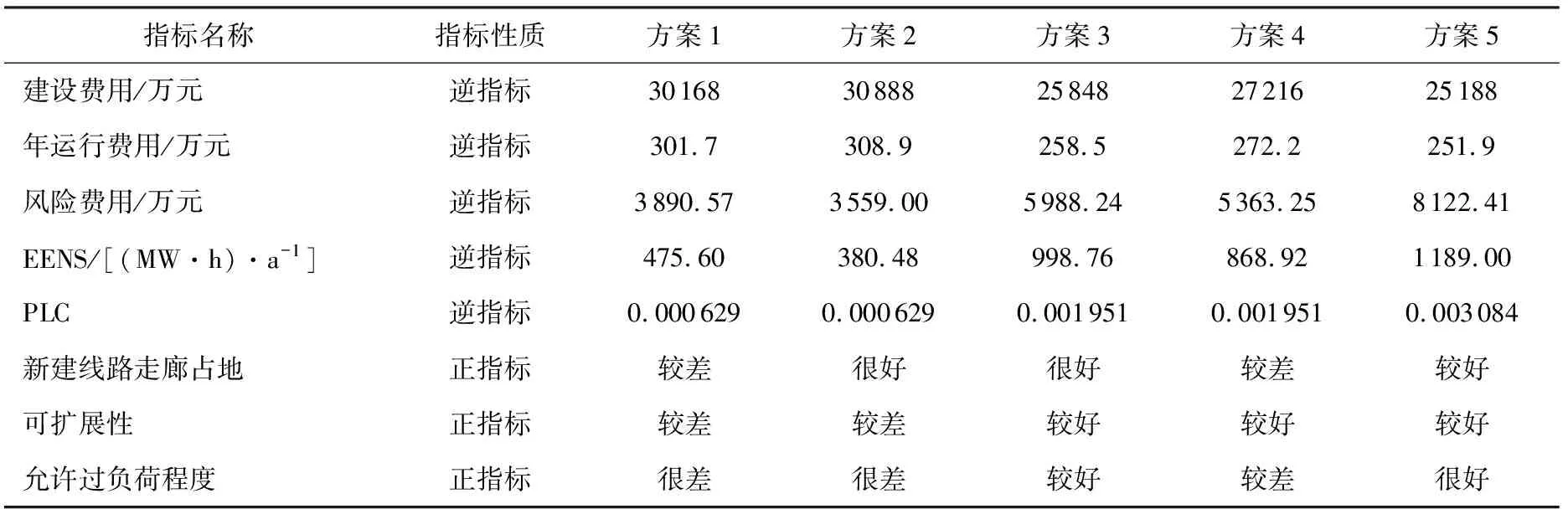
表1 规划方案评价指标体系

对于非定量指标，如新建线路走廊占地、可扩展性、允许过负荷程度等，通过选取模糊集来将其转化为定量指标。本文选取模糊集{1，2，3，4}分别对应很差、较差、较好、很好4个等级。

用本文提出的方法对各个方案进行综合决策，具体过程如下。

首先根据式(1)～(3)计算得到各指标对规划目标的权重系数ω=(0.006 6 0.006 6 0.162 1 0.330 0 0.089 3 0.089 6 0.036 3 0.279 5)。

以方案1为例，根据式(4)和式(5)得到无量纲归一化后方案指标矩阵，再对其第1列进行4次扩展并增加摄动，模拟4个专家对方案1的各个指标进行打分，得到评价样本矩阵

用N=1，2，3，4表示模糊灰类序号，即有4个描述规划方案优劣的模糊灰类，分别为{很好，较好，较差，很差}，以下为各自的白化权函数。

(1)N=1(很好)：灰数⊗∈[0,9,∞)，由灰数类型可知白化权函数属于类型1。

(2)N=2(较好)：灰数⊗∈[0,7,10]，由灰数类型可知白化权函数属于类型3。

(3)N=3(较差)：灰数⊗∈[0,5,8]，由灰数类型可知白化权函数属于类型3。

(4)N=4(很差)：灰数⊗∈[0,1,5]，由灰数类型可知白化权函数属于类型3。

然后将评价样本矩阵中的数据代入式(6)和式(7)得到方案1的灰色评价权矩阵

由式(8)得方案1所属模糊灰类的评价结果为

B1=ωR1=(0.407 1 0.322 2 0.142 6 0.128 0)。

其他方案采用相同评价方法，结果见表2。根据表2中结果对输电网规划方案进行决策，可以采用如下2种方法。

(1)最大隶属度法。依据最大隶属度原则，由表2中的结果可知方案1、方案2属于“很好”等级，方案3、方案4、方案5属于“较好”等级，而且方案2中“很好”所占权重大于方案1，所以方案2优于方案1。由此可得，5个方案按从优至劣的方式排序为方案2、方案1、方案3、方案4、方案5。

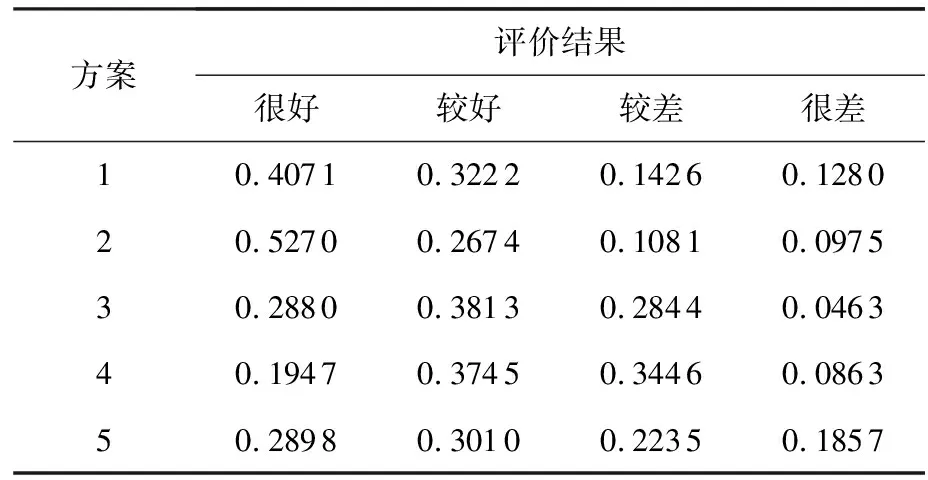
表2 各个方案的综合评价结果

(2)方案得分法。规定模糊灰类“很差”、“较差”、“较好”、“很好”分别对应{1分，2分，3分，4分}，用方案的模糊灰类权重乘以相应分数再进行加和即是该方案得分。由表2结果可以统计每个方案得分情况，再根据方案的得分高低进行评价。由此可得，5个方案按从优至劣排序为方案2(3.22分)、方案1(3.01分)、方案3(2.91分)、方案5(2.69分)、方案4(2.68分)。

3 结论

本文将熵权法、指标归一化和灰色模糊评价理论相结合应用于输电网规划综合决策中，避免了以往方法确定权重时的主观性；采用灰色模糊综合评价方法，解决输电网规划方案中信息量的不充分性和不明确性问题；对原始方案指标矩阵进行无量纲归一化，既消除了分析时量纲和数量级带来的影响，还能体现指标值的优劣性，使评价结果更加合理。

接下来的研究工作是进一步扩展综合评价指标体系以及对决策方法的改进。加入更多能体现输电网规划方案优劣的评价指标，使综合评价指标体系更加饱满、丰富；对本文采用的最大隶属度法和方案得分法进行修改，综合各自的优点提出更加科学、易行、有效的方案决策方法。

参考文献：

[1]张文全.电力技术经济评价理论、方法与应用[M].北京:中国电力出版社，2004：7-11.

[2]程浩忠.电力系统规划[M].北京：中国电力出版社，2008：221-235.

[3]谢敏，钟金，吴复立，等.基于改进单纯形法的输电网规划项目经济评估[J].电力系统自动化，2006，30(7)：10-15.

[4]邵宏.浅谈电网规划的经济评价[J].电力学报，2005，20(4)：367-368.

[5]杨宗霄，毛智杰，杨本渤，等.基于因子分析与神经网络的输电网安全评[J].电网技术，2009，33(14)：26-30.

[6]范宏，程浩忠，张节潭，等.考虑电力系统安全的输电网规[J].电力系统自动化，2009，31(11)：35-39.

[7]张强，韩学山，马志波，等.电网输电能力综合评价系统的开发[J].山东电力技术，2007(6)：3-6.

[8]肖峻，王成山，周敏.基于区间层次分析法的城市电网规划综合评判决策[J].中国电机工程学报，2004，24(4)：50-57.

[9]肖峻，罗凤章，王成山.一种基于区间分析的电网规划项目决策方法[J].电网技术，2004，28(7)：62-67.

[10]范利国，牛东晓.基于区间层次分析法的输电网规划综合评价决策[J].继电器，2007，35(12)：47-51.

[11]李晓辉，张来，李小宇，等.基于层次分析法的现状电网评估方法研究[J].电力系统保护与控制，2008，36(14)：57-61.

[12]伍力，吴捷，周乐荣.输变电工程项目的模糊多目标综合评判决策[J].电网技术，1999，23(3)：19-22.

[13]聂宏展，吕盼，乔怡，等.基于熵权法的输电网规划方案模糊综合评价[J].电网技术，2009，33(11)：60-64.

[14]黄武钟，钟丹虹，吴捷，等.模糊综合评判在电网远期规划中的应用[J].供用电，2001，18(5)：7-9.

[15]高赐威，程浩忠，王旭.盲信息的模糊评价模型在电网规划中的应用[J].中国电机工程学报，2004，24(9)：24-29.

[16]汉泽西，张娟.测量不确定度及其评定[J].电子测试，2011(6)：34-38.

[17]邓聚龙.灰色系统基本方法[M].武汉：华中理工大学出版社，1996.

[18]周建平，林韩，温步瀛.基于层次分析法与灰色关联理论的输电网规划方案综合决策[J].电网与清洁能源，2011，27(9)：66-70.

[19]熊平，刘顺利，张冲，等.基于最大隶属度的对空目标射击有利度模糊评估法[J].现代防御技术，2005，33(2)：9-13.