Calibration for Tri-Axial Magnetometer Based on Adaptive Genetic Algorithm*

LU Zhaoxing，ZHANG Jinsheng，WANG Shicheng，CAI Xinhua

(The Second Artillery Engineering University，Xi’an 710025，China)

Calibration for Tri-Axial Magnetometer Based on Adaptive Genetic Algorithm*

LU Zhaoxing，ZHANG Jinsheng*，WANG Shicheng，CAI Xinhua

(The Second Artillery Engineering University，Xi’an 710025，China)

Tri-axial magnetometers are widely studied and used in geomagnetic measurement.The influence on the measurement results caused by tri-axial nonorthogonality is analyzed，and the calibration formula is established.An optimization mathematical model is established to get the nonorthogonal error angles，and the Adaptive Genetic Algorithm is used to solve the model，in order to achieve the identification of intrinsic parameters and the calibration of measurement errors.The measurement experiment of FGM-2000 tri-axial magnetometer is done to verify the calibration method，and results show that the effect is obvious，the measurement error is reduced 88.1%and the measurement accuracy is significantly improved.

tri-axial magnetometer;adaptive genetic algorithm;parameter identification;error calibration

近年来，随着自动控制、工程检测、电子技术的发展，三轴磁强计被广泛应用于地磁导航等诸多新领域，在空间磁场的测量与研究中发挥着重要作用［1-4］。准确测量空间地磁场值或得到完整的地磁场信息，需要使用严格正交的三轴磁强计［2］。但是由于生产水平和安装工艺的限制，实际应用的三轴磁强计不严格正交［3］。文献［4］中列出了一些厂家生产的三轴磁强计三轴间夹角，大多数的磁强计的非正交误差都超过了1°，这使得三轴磁强计的实际测量数据存在较大测量误差。因此，三轴磁强计在使用时，必须对测量误差进行校正。

通常采用数值计算的方法，结合实验对三轴磁强计的测量误差进行校正［4-8］。近年来，生物学、人工智能、神经网络等理论的发展与应用，为三轴磁强计的误差校正开辟了新的思路。文献［9］提出了一种基于蚁群算法的三轴磁强计正交误差校正方法，能较好地实现对三轴磁强计正交误差的校正。遗传算法作为一种基于生物遗传和进化机制的概率优化技术，具有运算简单、搜索过程灵活、搜索效率高以及隐含并行性等特点，是一类可以用于复杂系统优化计算的算法［10］，特别适用于解决三轴磁强计参数辨识问题。但一般遗传算法的交叉概率和变异概率固定，不能反映种群的进化进程，容易产生早熟收敛和收敛速度慢的缺陷［11］。因此，本文在应用遗传算法对问题进行求解时，针对一般遗传算法存在的不足进行了改进。改进后的自适应遗传算法能自动地获取和积累相关搜索空间信息，采用动态自适应技术控制参数选择，求得全局最优解［12-13］。这种方法可以保护优良个体有效提高搜索效率和避免“早熟”现象。因此，本文通过引入高精度的标量磁力仪提供期望输出，采用自适应遗传算法实现对三轴磁强计测量误差的校正。

1 三轴磁强计的测量误差分析与校正

三轴不正交是三轴磁强计测量误差的主要来源之一，本文着重分析和校正由于磁强计三轴不正交所造成的测量误差。设三轴磁强计的3个测量轴分别为OX，OY和OZ，与磁强计的测量坐标系对应的理想正交坐标系的3个正交轴分别为OX1，OY1和OZ1，两个坐标系之间的位置关系如图1所示。①OZ1轴与OZ轴重合;②坐标面Y1OZ1与坐标面YOZ共面，且OY轴与OY1轴之间夹角为β;③OX轴在坐标面Z1OX1的投影与OX1轴之间的夹角为α; OX轴与坐标面Z1OX1之间的夹角为γ。

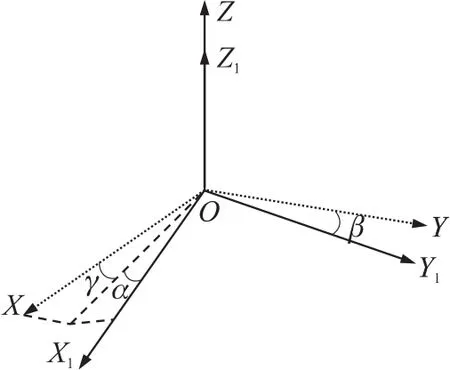
图1 磁强计三轴与正交轴之间位置关系

设三轴磁强计3个坐标轴的测量输出分别为Bx，By和Bz，对应理想传感器的三轴输出分别为B1x，B1y和B1z，则二者之间的对应关系如式(1)所示。

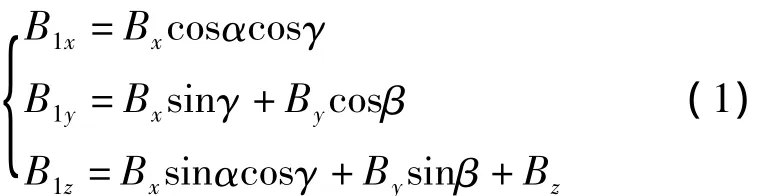
式中α，β和γ即为非正交坐标系和正交坐标系之间的非正交误差角。

令

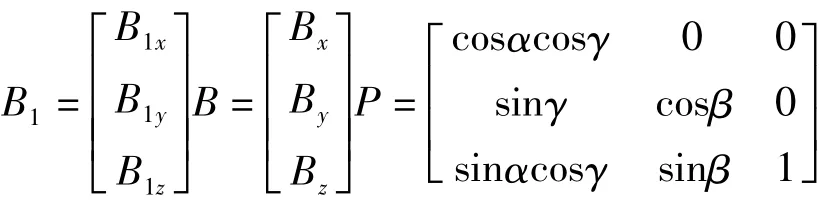
则式(1)可写成向量形式:

由此得到，三轴磁强计的误差校正公式，在已知三轴磁强计非正交误差角的情况下，由式(2)即可实现由测量值B到理想值B1之间的转换。

仅依赖对被校正仪器提供的测量数据进行处理而得到期望输出得方法，不能有效消除系统误差的影响。借助高精度GSMP-35光泵磁力仪提供被校正磁强计的期望输出，建立三轴磁强计非正交误差角求解的最优化模型:

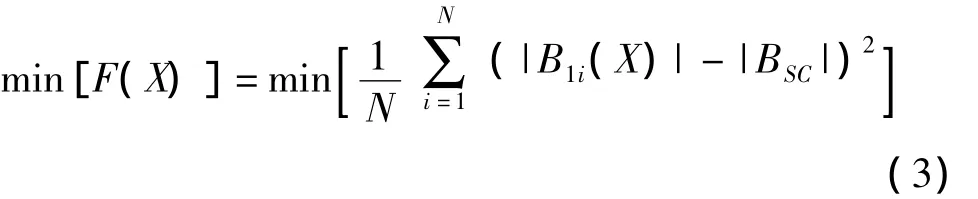
式中，参数向量X=［α，β，γ］T，|B1i(X)|为测量量Bi经过校正后的总场强度，|BSC|为GSMP-35光泵磁力仪测量得到的背景场场强。当目标函数F(X)→0时，|B1i|→|BSC|，此时，校正参数X的值即为三轴磁强计的非正交误差角。

2 误差模型参数辨识

模型(3)为典型的无约束单一目标最优化问题，遗传算法作为一种应用广泛的智能算法，能够较好地解决这一类问题。但是，基本遗传算法的收敛性和稳定性并不理想［14］，而自适应遗传算法能够较好地弥补这一不足［15］。因此，采用自适应遗传算法通过改进交叉与变异遗传算子来对模型(3)进行求解。

2.1 自适应遗传算法

遗传算法本质上是一种高效、并行、全局搜索的方法，能够在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最优解［13］。基本遗传算法的一般计算流程如图2所示。

在遗传算法的参数设置中交叉概率Pc和变异概率Pm的选择是影响遗传算法行为和性能的关键所在，直接影响算法的收敛性［16］，主要体现在两个方面:

(1)对于交叉概率Pc而言，Pc越大，新个体产生的速度就越快，但Pc过大时，遗传模式被破坏的可能性也越大，使得具有高适应度的个体结构很快就会被破坏;Pc过小时，会使得搜索过程缓慢，以致停滞不前;

(2)对于变异概率Pm而言，如果Pm过小，就不易产生新的个体结构;如果Pm过大，遗传算法就会失去智能性，退化成纯粹的随机搜索算法。

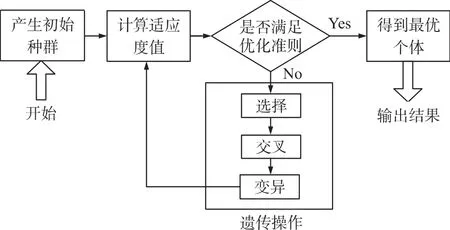
图2 一般遗传算法计算流程图

不同于一般的遗传算法，自适应遗传算法能够根据个体适应度值自动调节Pc和Pm值，其调节的基本思想为:

(1)当种群各个个体适应度趋于一致或者趋于局部最优时，使Pc和Pm增大，而当群体适应度比较分散时，使Pc和Pm减小;

(2)对于适应度高于群体平均适应度值的个体，对应于较小的Pc和Pm，使该解得以保护进入下一代;而低于平均适应度值的个体，相对应于较大的Pc和Pm，使该解被淘汰掉。

因此，自适应的Pc和Pm能够提供相对某个解的最佳Pc和Pm，在保持群体多样性的同时，也保证算法良好的收敛性［12］。

在自适应遗传算法中，Pc和Pm按照式(4)和式(5)进行自适应调整［14］:

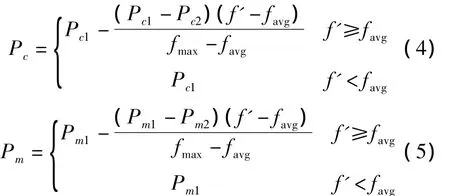
式中fmax为群体中最大的适应度值，favg为每代群体的平均适应度值，f'为要进行交叉的两个个体中较大的适应度值，f为要变异个体的适应度值。常值参数取值为Pc1=0.9，Pc2=0.6，Pm1=0.1，Pm2= 0.001。

2.2 算法求解步骤

结合图2的算法流程，应用自适应遗传算法对三轴磁强计的非正交误差角进行求解的具体算法步骤如下:

第1步产生初始种群并对参数进行编码

确定种群规模M=80。随机产生80个个体组成初始种群，种群代数k=1，并设定最大种群代数kmax=1000和适应度梯度限Δ¯G=5×10-5。采用遗传算法常用的二进制编码方式对种群个体进行编码。设定α、β和γ的搜索范围均为-0.1 rad～0.1 rad，参数的二进制编码长度为l=10，则参数的求解精度如式6所示。

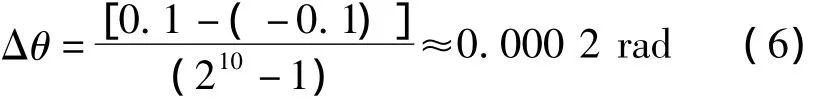
用二进制码串SL=，，}作为染色体表示参数α、β和γ，其中基因段={aα1，aα2，…，aα10}，={aβ1，aβ2，…，aβ10}，={aγ1，aγ2，…，aγ10}，aαi， aβi，aγi∈{0，1}。编码位串到实际参数值之间的转换关系由解码函数Γ来确定，转换过程如式(7)所示:

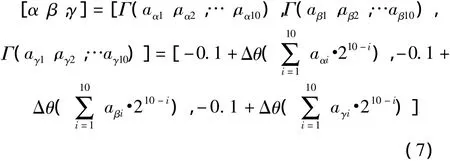
第2步计算适应度值

适应度函数的选取直接影响到遗传算法的收敛速度以及能否找到最优解。一般而言，适应度函数是由目标函数变换而成的。由于模型(3)最小值问题，因此建立适应度函数G(X)如式(8):

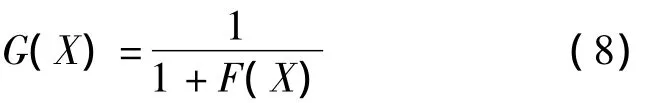
将种群个体对应的参数值代入到适应度函数(8)中得到第k代种群的第i个个体对应的适应度值G(k)i(X(k))，求平均得到第k代种群的平均适应度值¯G(k)。

第3步选择

根据适应度值，计算得到种群中各个个体的选择概率Pi1和累计概率Pi2，计算公式如式(9):

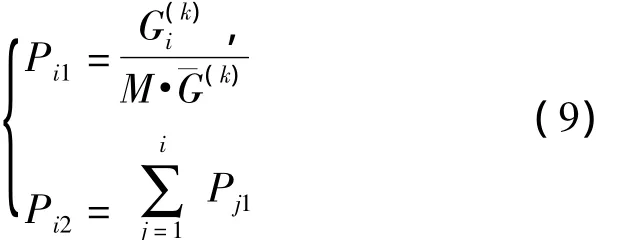
采用轮盘赌选的方法选择交配个体。进行80轮选择，每一轮随机产生一个0到1之间的随机数，将该随机数作为选择指针来确定被选个体，产生由80个被选个体组成的交配种群。

第4步交叉(基因重组)

采用二进制单点交叉的方式进行。将交配种群进行随机两两配对，得到40组配对个体。选择各组配对个体中较大的适应度值为该组配对个体的f'i(i=1，2，…，40)。将各个组的f'i以及fmax、favg代入到式(4)得到各组配对个体的交叉概率Pci。按照交叉概率对配对个体进行基因重组，交叉点随机确定。交叉之后得到80个基因重组后的子代个体。

第5步变异

采用单基因位的二进制变异进行。变异即意味着单个基因位0和1之间的翻转。对于每个个体的变异都是随机进行的，个体的变异概率Pm由式(5)计算得到。经过变异后，得到新一代的种群。

第6步判断遗传是否结束

判断k是否满足k=kmax，若不满足，k=k+1，转到第3步;若满足，判断¯G(k)-¯G(k-1)＜Δ¯G是否满足，若满足转到第7步，若不满足，k=k+1，kmax= 2kmax，转到第3步。

第7步结果输出

在所有代种群的所有个体中，选择适应度最大的个体及其对应的α、β、γ值作为求解结果输出。

自适应遗传算法的算法流程图如图3所示。

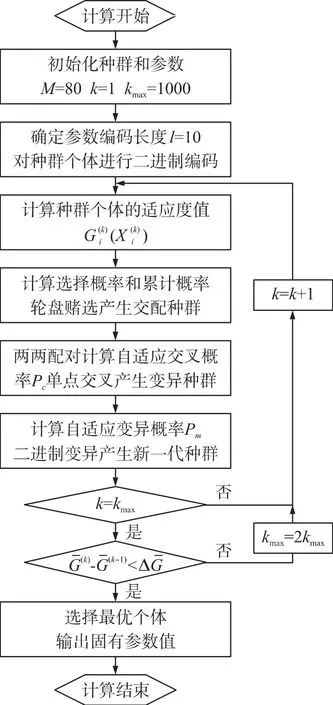
图3 自适应遗传算法流程图

3 实验验证与结果分析

以FGM-2000三轴磁通门磁强计的误差校正为对象开展实验，实验系统如图4所示。

实验的具体步骤如下:

第1步选定稳定均衡背景磁场作为实验场地，将固定有FGM-2000三轴磁强计的无磁转台固定于实验地点，打开实验仪器，检验仪器性能。

第2步待仪器性能稳定后，每隔10°转动一次转台，磁强计读数稳定后记录对应姿态下的三轴输出，完整记录磁强计旋转360°得到的测量数据，如图4(a)所示。

图4 实测实验示意图

第3步保持转台在测量点位置不变。取下FGM-2000三轴磁强计，将GSMP-35光泵磁力仪固定在无磁转台上，以第2步中的方法将转台旋转360°，记录对应姿态下磁力仪测量得到的总场数据，如图4(b)所示。

第4步结合测量得到的磁场数据，运用自适应遗传算法对三轴磁强计的非正交误差角进行求解。

求解得到的结果如图5和表1、表2所示。

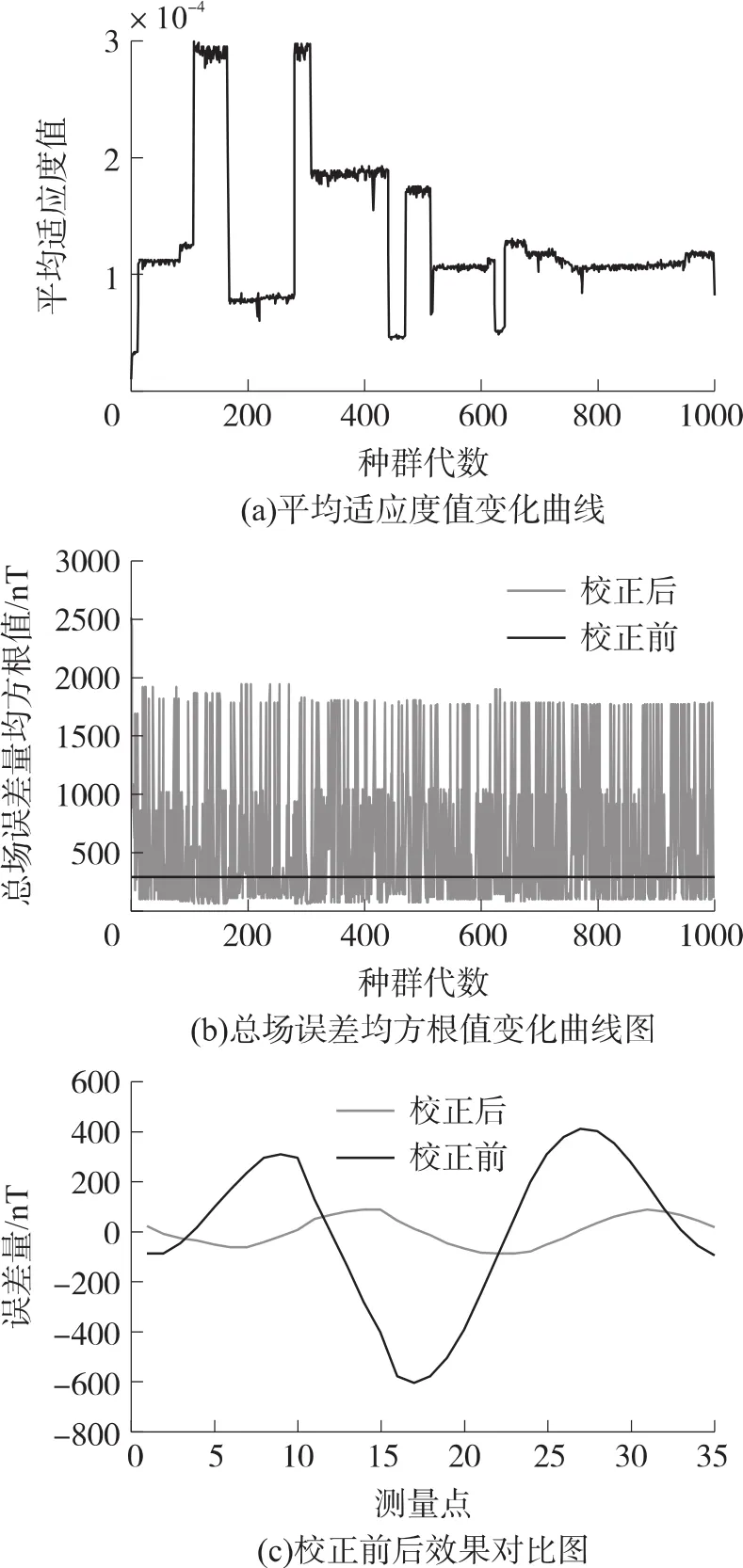
图5 校正结果示意图

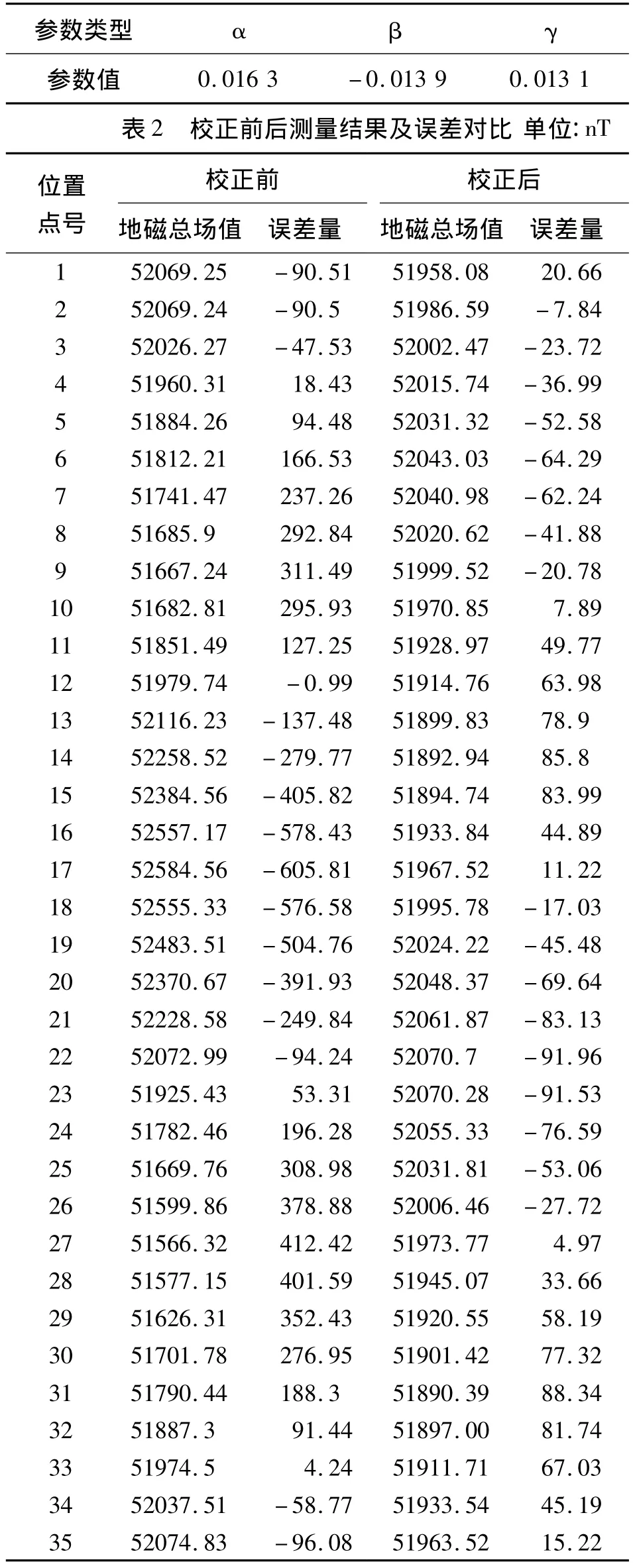
表1 FGM-2000三轴磁力仪非正交误差角最优求解值

分析校正结果可知，自适应遗传算法在求解三轴磁强计的固有参数时，具有良好的稳定性。遗传1 000代之后，地磁总场测量值均方根误差可由校正前的411.82 nT，减小为校正后的49.38 nT，测量误差减小了88.1%，测量精度显著提高。

分析求解得到的磁强计法固有参数可知，3个非正交误差角均为小角度。因此，可以通过将校正式(2)中的参数进行线性化近似处理，即sinα≈α， sinβ≈β，sinγ≈γ，cosα=cosβ=cosγ≈1，来提高算法收敛性能和搜索速度。

经校正之后，磁强计的测量误差仍有50 nT左右，分析原因主要有3个方面:①有限测量数据不可能完全反映矢量传感器全部姿态下的输出特性;②除正交误差外，测量数据中包含有其他性质的测量误差，如三轴的标度系数不一致、零点漂移、背景场的时变以及传感器的温漂等;③提供期望输出的高精度光泵磁强计自身也存在一定的测量误差。

4 结论

本文提出的三轴磁强计的误差校正方法，运用自适应遗传算法求解三轴磁强计的非正交误差角，进一步实现对三轴磁强计测量误差的校正。通过FGM-2000三轴磁力仪的实际测量实验对校正方法进行验证，结果表明，该方法效果明显，能够实现三轴磁强计非正交误差角的有效辨识和测量精度的显著提高，从而为发挥三轴磁强计自身优势和拓展应用领域提供了一条切实可行的技术途径。

［1］吴德会，黄松岭，赵伟.基于FLANN的三轴磁强计误差校正研究［J］.仪器仪表学报，2009，30(3):449-453.

［2］林春生，向前，龚沈光.三轴磁强计正交误差分析与校正［J］.探测与控制学报，2005，27(2):9-12.

［3］Gu Wei，Chu Jianxin，Huang Hui.Development of Three-Tip Fluxgate Magnetometer Applied on Ship Magnetic Field Measure［C］//IEEE International Instrumentation and Measurement Technology Conference，2011:919-924.

［4］朱昀，董大群.三轴磁强计转向差的自适应校正［J］.仪器仪表学报，1999，20(4):392-396.

［5］周庆飞，汪海涛，梁斌.磁通阀式磁传感器最小二乘校正［J］.探测与控制学报，2009，31(2):63-70.

［6］周榕军，刘大明，洪泽宏.非理想条件下三轴磁通门传感器误差修正方法［J］.舰船科学与技术，2011，33(3):85-89.

［7］吴德会.基于SVR的三轴磁通门传感器误差修正研究［J］.传感器与微系统，2008，27(6):43-46.

［8］胡海滨，林春生，龚沈光.基于共轭次梯度法德非理想正交三周磁传感器的修正［J］.数据采集与处理，2003，18(1):88 -91.

［9］周建军，林春生，张坚.基于蚁群算法对三轴磁强计非正交度的修正［J］.舰船科学技术，2011，33(2):106-109.

［10］Kwok H S，Tang W K S.A Fast Image Encryption System Based on Chaotic Maps with Finite Precision Representation［J］.Chaos，Solitons and Fractals，2007，32(4):1518-1529.

［11］李志宇，史浩山.一种基于网格和移动代理的无线传感器网络数据融合算法［J］.传感技术学报，2008，21(7):1232-1236.

［12］史建国，高晓光，李相民.“预先”进化遗传算法研究［J］.宇航学报，2005，26(2):168-173.

［13］徐定杰，刘明凯，沈锋.基于自适应遗传算法的DGPS整周模糊度快速解算［J］.航空学报，2013，34(2):371-377.

［14］王小平，曹立明.遗传算法——理论、应用与软件实现［M］.西安:西安交通大学出版社，2002(1):68-85.

［15］Cheung A，Bennamoun M，Bergmann N W.An Arabic Optical Character Recognition System Using Recognition-based Segmentation［J］.Pattern Recognition，2001，34(2):215-233.

［16］王军号，孟祥瑞.一种基于改进遗传RBF神经网络的传感器动态特性补偿算法［J］.传感技术学报，2010，23(9):1298 -1302.

卢兆兴(1990-)，男，山东莒县人，博士研究生，主要研究方向为导航、制导与控制;

张金生(1980-)，男，河南南阳人，副教授，博士，主要研究方向为导航、制导与控制;

王仕成(1962-)，男，山东单县人，教授，博士生导师，主要研究方向为导航、制导与控制。

基于自适应遗传算法的三轴磁强计误差校正方法*

卢兆兴，张金生*，王仕成，蔡欣华
(第二炮兵工程大学精确制导与仿真实验室，西安710025)

三轴磁强计已被广泛应用于空间磁场的测量。分析三轴不正交对三轴磁强计测量结果带来的影响，得到三轴磁强计的误差校正公式，建立求解非正交误差角的最优化数学模型，并运用自适应遗传算法对模型进行求解，实现对磁强计固有参数的辨识和测量误差的校正。通过FGM-2000三轴磁力仪实测实验对校正方法进行验证，结果表明，校正方法效果明显，仪器的测量误差减小了88.1%，测量精度显著提高。

三轴磁强计;自适应遗传算法;参数辨识;误差校正

TM936

A

1004－1699(2014)03－0331－06

2013-06-27修改日期:2013-08-24

C:5180

10.3969/j.issn.1004－1699.2014.03.011

项目来源:国家自然科学基金青年科学基金项目(61004128)