空泡外形对超空泡航行体机动回转运动影响

李雨田，张宇文

(1.中船重工第七一○研究所，湖北 宜昌 443003；2．西北工业大学 航海学院，西安 710072)

常规水下航行体的流体介质完全是水，航行体表面为全沾湿，流体介质作用于整个航行体表面。超空泡航行体表面大部分由空泡包围，流体介质由水变为汽/气体。汽/气体密度较水密度小两个量级，而据空泡生成机理，空泡内压力为常数，航行体表面所受汽/气体压力处处相等。超空泡航行体的力学特征使超空泡航行体流体动力设计原理及方法完全不同于常规水下航行体。常规水下航行体流体动力依赖于航行体外形，流体动力设计主要为航行体外形设计。超空泡航行体流体动力则决定于空泡生成后航行体的沾湿表面，外形设计主要为航行体沾湿表面设计。沾湿表面不仅决定于航行体外形，亦决定于空泡外形。

为此提出“超空泡航行体空泡流型”概念，将超空泡航行体流体动力所涉航行体外形、空泡外形、航行体外形与空泡外形匹配关系统一为一体，用超空泡航行体空泡流型描述，以航行体空泡流型为主导进行超空泡航行体流体动力设计。由空泡自身特性出发研究与确定航行体可生成空泡流型尤其可稳定的航行体空泡流型；再由航行体运动力学原理出发研究与确定航行体空泡流型可满足航行体实现稳定运动的要求；研究航行体空泡流型与航行体外形及空泡生成系统的关联性尤其定量关系，提出所需空泡流型。

因超空泡航行体作直航运动，需设计直航空泡流型，保证此空泡流型下超空泡与航行体沾湿面积，使空泡、航行体与周围流体维持力系平衡，以实现超空泡航行体稳定直航运动。超空泡航行体作机动回转运动，操纵控制面提供航行体机动法向过载，航行体机动变向，空泡外形随之变化，当空泡外形与航行体外形动态匹配到一定量值，满足稳态机动回转运动所需沾湿面时动态过程结束，转入稳定机动回转运动。欲实现超空泡航行体由直航过渡到机动回转及稳定机动回转运动，需研究过渡、机动运动过程中空泡外形变化及影响变化因素，研究空泡外形与航行体外形的匹配关系。

1 超空泡机动回转运动数学建模

1.1 超空泡体坐标系

设超空泡航行体以角速度ω、回转半径R作机动回转运动，考虑空泡截面独立扩张原理[1-2]及空泡延迟效应[3-5]，最终稳态超空泡呈近似圆弧状的“月牙形”[6-7]。建立地面坐标系O0x0y0z0见图1，坐标原点O0位于回转运动中心，O0x0z0平面为水平面；建立航行体坐标系Obxbybzb，坐标原点Ob位于航行体浮心，Obxb轴沿航行体纵轴并指向航行体头部；Obyb垂直于Obxb并指向上方，Obzb垂直于Obxbyb平面，正方向由右手法则确定；建立超空泡体坐标系Orl，坐标原点O位于空泡截面中心，l轴沿空泡轴向，指向空泡尾部，表征空泡轴线(中弧线)长，r轴沿空泡截面径向，表征l处空泡半径。在超空泡体坐标系中，基于空泡截面独立扩张原理建立的超空泡外形公式仍适用，但超空泡轴线非直线，为曲线。

图1 超空泡体坐标系

1.2 超空泡外形数学表达式

据空泡截面独立扩张原理，空泡在超空泡体坐标系中的截面扩张方程为

(1)

式中：S0为起始空泡面积；t为空泡轴向扩张时间；Δp为空泡内外压差；ρ为周围流体密度。

超空泡半径为

(2)

式中：Rm为空泡最大半径；Rn为空化器半径；tm为空泡扩张至最大半径时间；η为经验系数。

超空泡径向截面外点、内点在超空泡体坐标系Orl中坐标为

(3)

超空泡体坐标系至地面坐标系转换矩阵为

(4)

超空泡径向截面外点、内点在地面坐标系中的坐标为

(5)

(6)

式(5)、(6)已完全定义出以角速度ω、半径R作机动回转运动的超空泡在地面坐标系中的几何外形。

2 直航运动过渡到机动回转运动过程超空泡外形变化

研究超空泡航行体由直航运动转入机动回转运动过程中空泡外形变化。在航行体转动过程中航行体头部空化器随之转动，迎流方向不断改变。据空泡截面独立扩张原理及空泡延迟效应知，航行体超空泡截面扩张规律仅依赖于所论时刻条件，空泡截面后续发展仅与该截面初生时刻条件有关，与此时刻之前或之后条件几乎无关。因此，航行体头部空化器在转动过程中每时刻产生的新空泡截面方向不断改变，与迎流垂直，其余空泡截面扩张、收缩规律均仅依赖于此前的直航状态条件。航行体由直航状态转入机动后空泡由头部起不断变形弯曲，并向后不断延伸，直至完全替代直航状态的超空泡。超空泡航行体由直航运动过渡到机动回转运动过程示意图见图2。

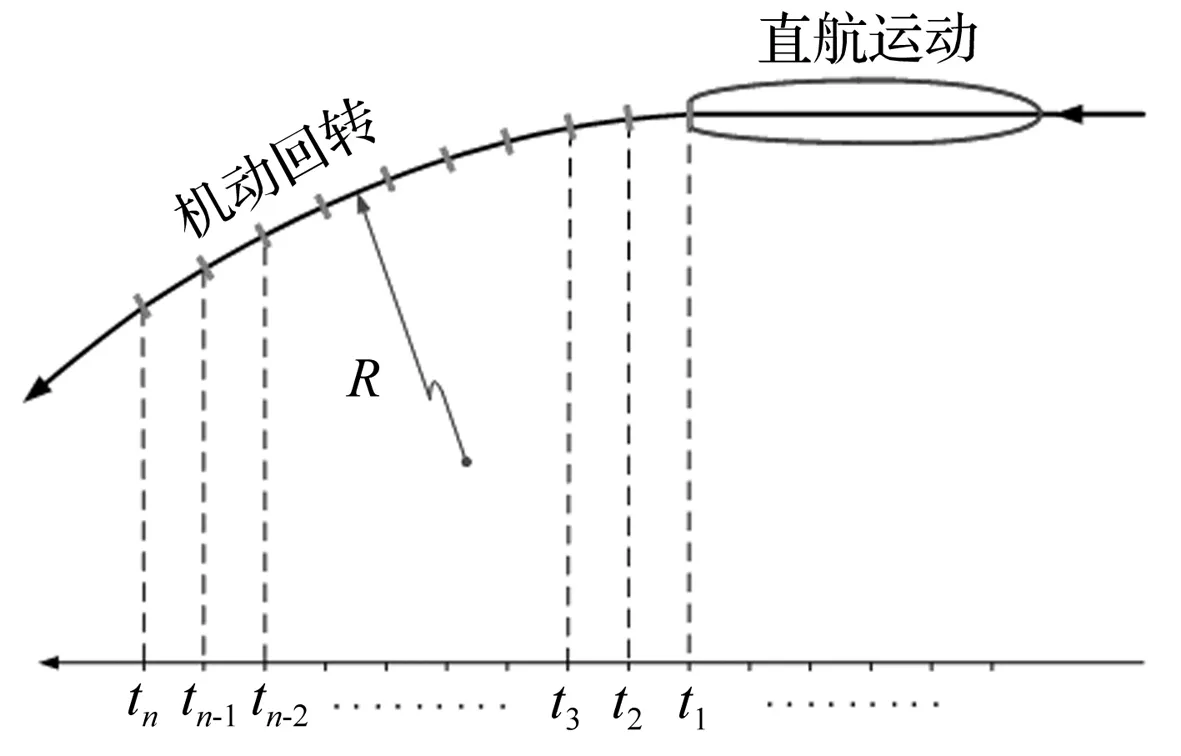
图2 直航转入机动回转运动

超空泡外形变化过程仿真见图3。图中第一幅实线表示直航状态空泡外形；中间各幅虚线部分表示回转运动中不断形成的新空泡截面，实线部分为原直航状态空泡；最后一幅中虚线为定常机动回转稳态超空泡。由图3看出，随超空泡航行体回转运动开始，回转运动状态下新空泡截面不断产生并独立扩张，逐渐替代直航状态部分空泡，直到直航超空泡被完全替代，回转运动状态超空泡完全生成，形成稳态超空泡。若超空泡航行体机动过程中回转角速度不断变化，则航行体超空泡外形亦不断变化。若以定常角速度回转，则超空泡外形在完成由直航到机动的过渡后空泡外形不再改变，形成回转运动稳定超空泡外形。

图3 直航转入机动运动过程中超空泡外形变化

3 影响机动回转运动超空泡外形变化因素

影响超空泡外形变化因素较多，重力[8-9]、空化器攻角[10-12]影响空泡轴线上翘或下偏，空泡内外压扰动[13]影响空泡外形周期性变化。针对机动回转运动，角速度及离心力为衡量机动运动的重要技术指标，本文重点研究这其对超空泡外形变化影响。

3.1 角速度对超空泡外形影响

由于超空泡航行体跟踪目标主要在水平面内进行，常以水平面回转角速度衡量超空泡航行体的机动性。当超空泡航行体航速v一定时，角速度与回转半径关系为ωy=-v/R。

为对航行体机动运动时超空泡外形变化有直观、量级概念，航行体空化器直径为100 mm、空化数σ=0.023 8、航速v=100 m/s、角速度分别为ωy=0.5, 1, 1.5, 2 rad/s的机动回转运动空泡外形仿真见图4。由图4看出，机动回转运动中超空泡几何外形逐步由直线对称外形逐步被压弯呈 “月牙形”，其整体空泡外形关于空泡中弧线对称；空泡长度(中弧线长度)及其截面最大半径基本不随角速度变化；随角速度增大(回转半径减小)空泡轴线沿回转运动圆周逐渐由直线变为曲线，空泡最大弯度及最大相对弯度逐渐增大。

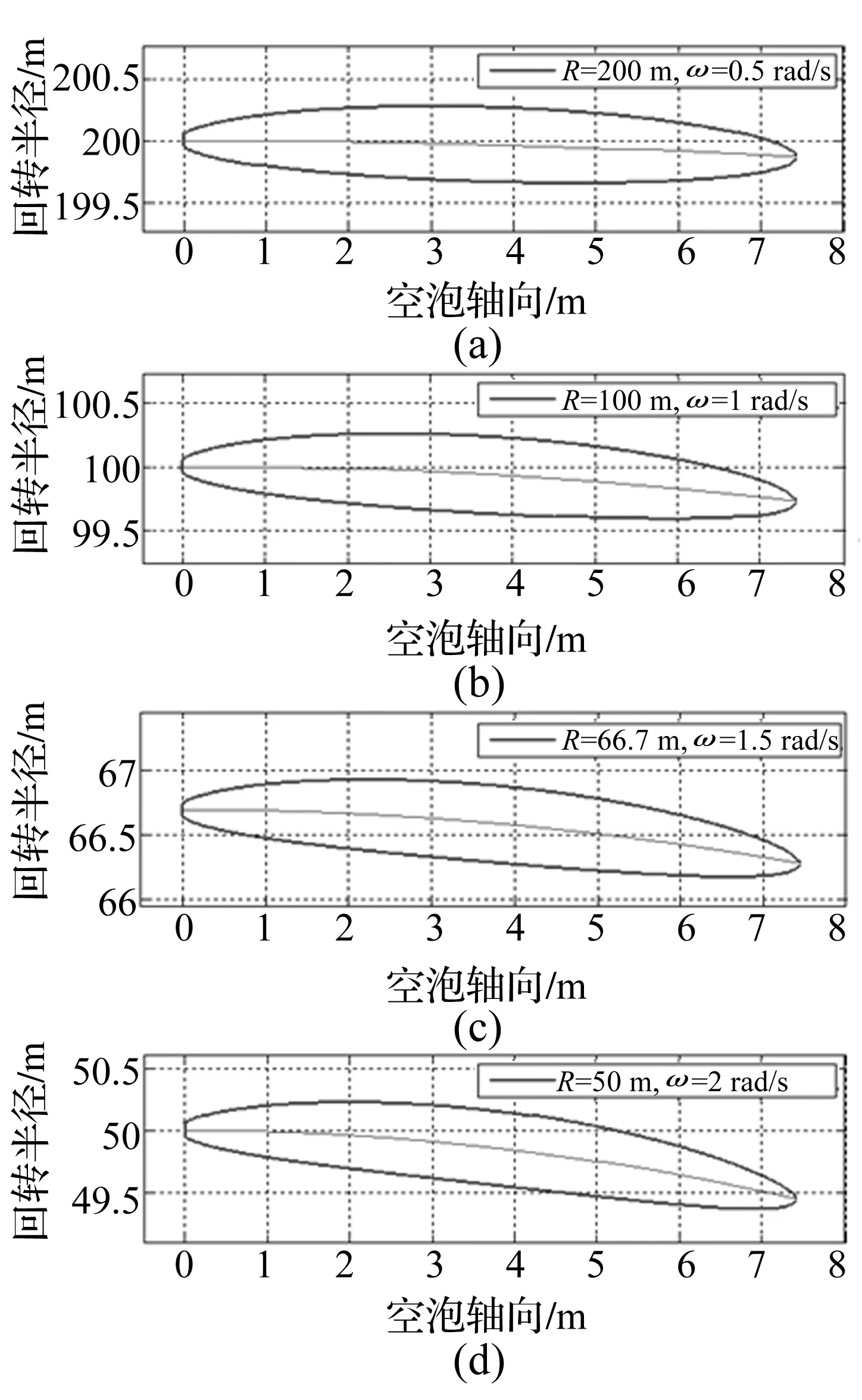
图4 不同角速度的超空泡外形

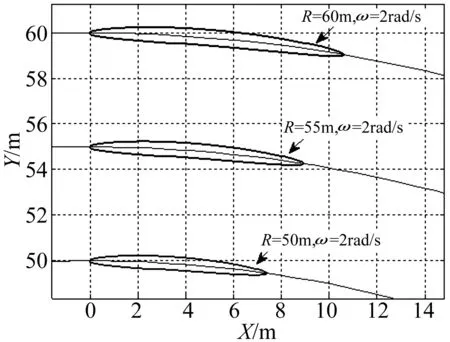
图5 不同航速的超空泡外形

角速度ωy=2 rad/s，航速分别为v=100, 110, 120 m/s的空泡外形仿真见图5。由图5看出，航速对空泡尺度影响较大，空泡最大直径、中弧线长度、弦长、最大弯度均随航速的增大而最大。故在研究超空泡航行体机动运动时，为保证空泡外形的稳定性通常设航行体航速不变。

3.2 离心力对空泡外形影响

超空泡航行体作机动回转运动见图6。由图6看出，空泡内表面(长虚线)与外表面(短虚线)的点因回转半径及线速度不同，内表面点速度小，外表面点速度大。据伯努利方程，空泡内表面压力大，外表面压力小，内外压力差形成沿回转半径方向合力(离心力)，从而对空泡外形产生影响；此外，空泡内气体具有一定质量，在回转运动过程中会产生惯性力，方向沿回转半径方向，对空泡外形亦产生一定影响。

图6 离心力对超空泡变形分析

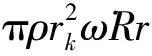
(7)

(8)

沿l轴积分,即

(9)

式中：rH(l)为空泡中弧线的移量；rk(l)为l处空泡截面半径。

为积分式(9)，需获得离心力Fl表达式。Fl由两部分组成，即由空泡内、外表面压力差形成的离心力Flp及由空泡质量产生的惯性力Flm。先计算Flp。为此在rk(l)截面建立局部坐标系oξη(图6)，oξ轴垂直于航行体回转运动平面，oη轴沿航行体回转半径方向，指向外侧。将空泡表面分为内、外侧，oξ轴之上为外侧。空泡外、内侧表面点的oξη坐标系中坐标为

(10)

空泡外、内侧表面点至航行体回转运动中心距离LRw，LRn分别为

(11)

空泡外、内侧表面点速度vkw，vkn分别为

vkw=ωLRw,vkn=ωLRn

(12)

据伯努利方程，空泡外表面压力pkw及内表面压力pkn间关系为

(13)

内外表面压力差Δpk为

2ρω2Rrk(l)sinθ

(14)

沿ξ，η方向压力分量为

(15)

离心力可通过单位长度空泡表面压力积分获得。沿ξ方向压力左、右侧表面对应点大小相等方向相反，沿表面积分合力为零。沿η方向压力积分即得空泡内、外表面压力差形成的离心力。

ρω2RVk(l)

(16)

式中：Vk为半径rk(l)的单位长度空泡体积。

空泡质量形成的单位长度空泡离心力Frm为单位长度空泡质量的惯性力，即

Flm=ρqVk(l)ω2R

(17)

式中：ρq为空泡内气体密度。

总离心力为式(16)与式(17)之和，即

Frl=ρω2RVk(l)+ρqω2RVk(l)=

(ρ+ρq)ω2RVk(l)

(18)

将式(18)代入式(9)，得回转运动离心力所致超空泡中弧线外移量计算式为

(19)

空化器直径100 mm、空化数σ=0.023 8、航速v=100 m/s、角速度分别为ωy=0.5、1、1.5、2 rad/s条件时离心力对超空泡外形影响(实线为原始空泡外形，虚线为考虑离心力影响下空泡外形)见图7。由图7看出，超空泡航行体机动回转运动时离心力使空泡中弧线沿径向向外侧偏移，偏移量由头部至尾部逐渐增大，在尾端达到最大值，具有使“月牙形”回转超空泡拉直作用。离心力所致中弧线变形量随回转角速度增大而增大，与回转角速度成正比的线性关系。

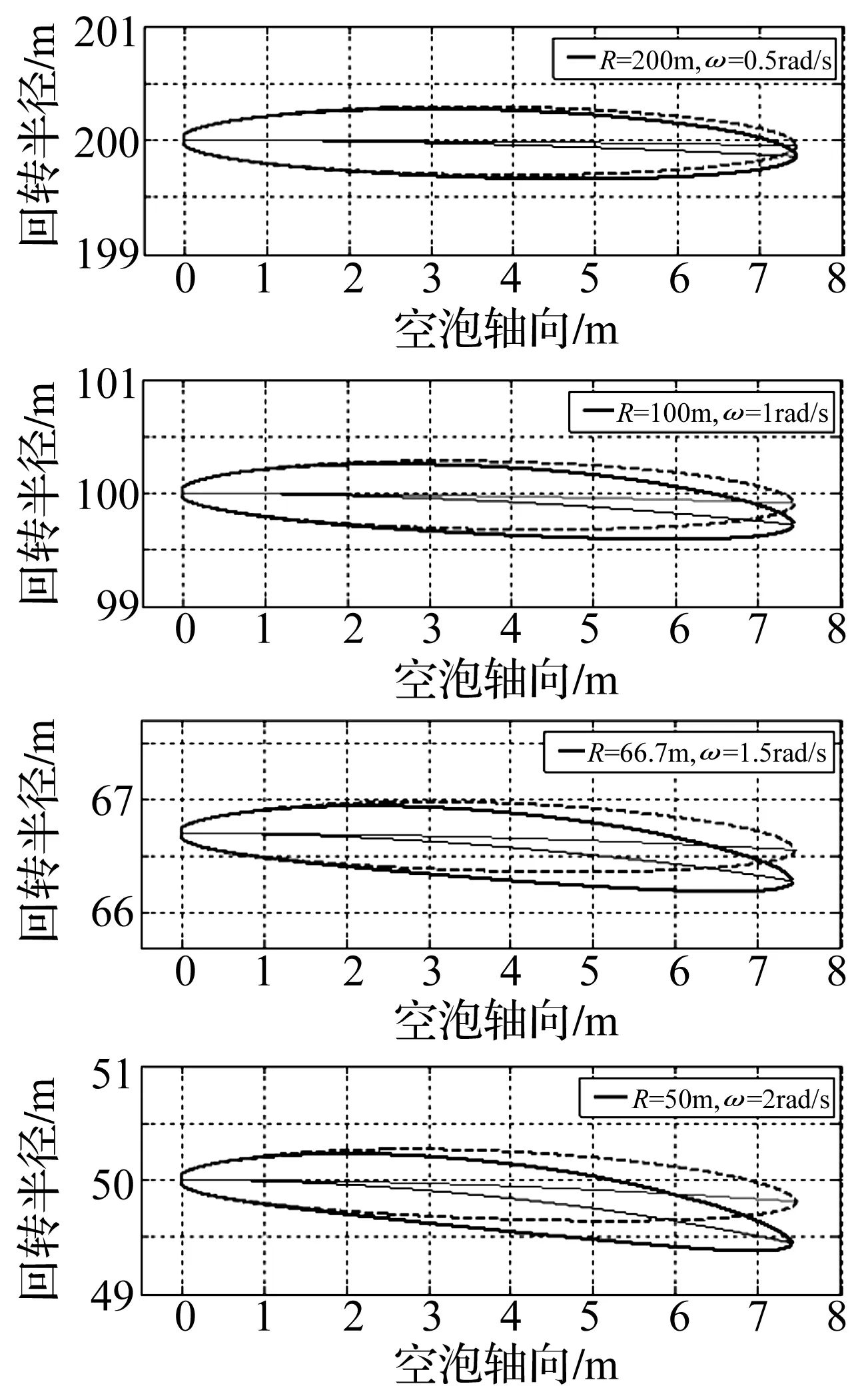
图7 离心力对超空泡外形影响

由离心力引发的空泡轴线偏移量沿空泡轴向变化值见图8。由图8看出，由离心力引发的空泡轴线偏移量沿空化器向航行体尾部逐渐增大，最大值约0.4 m，该偏移量与空泡半径值为同一数量级，故离心力对空泡外形影响较大，不可忽略。

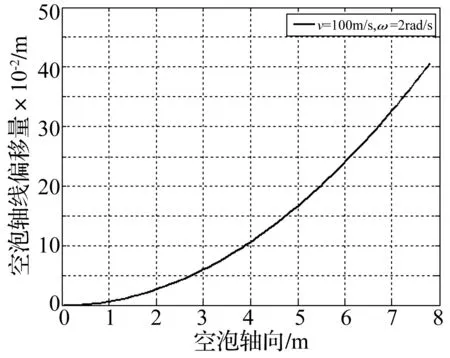
图8 离心力引发的空泡轴线偏移

4 给定空泡流型下超空泡航行体机动能力评估

4.1 机动能力评估方法

航行体机动能力为综合性指标，涉及诸多因素。此处针对超空泡变形，采用对机动回转运动造成的空泡变形对给定外形航行体机动能力影响作初步评估。

(1) 设超空泡航行体航速为100 m/s。

(2) 分别考察三种直航初始空泡流型：① 尾舵展长一半穿刺主体空泡的对称空泡流型；② 空泡闭合在尾部的对称空泡流型；③ 空泡闭合在尾舵根部前缘的对称空泡流型。

(3) 设航行体机动运动可能许可的三种空泡流型作为评判机动能力的空泡变形临界点：① 空泡闭合在尾部闭合的非对称空泡流型(航行体尾部闭合之前壳体无沾湿面)；② 空泡闭合在尾舵根部前缘的非对称空泡流型(航行体尾舵根部前缘之前壳体无沾湿面)；③ 空泡闭合在距尾部闭合三分之一圆柱段长度处非对称空泡流型(航行体距尾部闭合三分之一圆柱段长度之前壳体无沾湿面)。

(4) 设超空泡航行体自某时刻起由水平直航状态开始做机动回转运动，保持100 m/s线速度不变，用仿真计算获得航行体不同角速度回转时的空泡外形。

(5) 对航行体回转运动的空泡外形进行离心力、重力、空化器攻角等影响因素修正。

(6) 以临界回转角速度为航行体机动能力指标利用航行体回转运动修正后空泡外形，据(3)中空泡变形临界点评估航行体机动能力。

4.2 评估机动能力的三种初始直航状态空泡流型

据仿真计算结果，对给定的航行体外形设定三种初始直航对称空泡流型：尾舵半穿刺空泡流型、尾部闭合空泡流型及尾舵根部前缘闭合空泡流型。三种空泡流型对应的空化数分别为σ=0.016 5、σ=0.021 17及σ=0.021 65。三种初始直航空泡流型见图9。

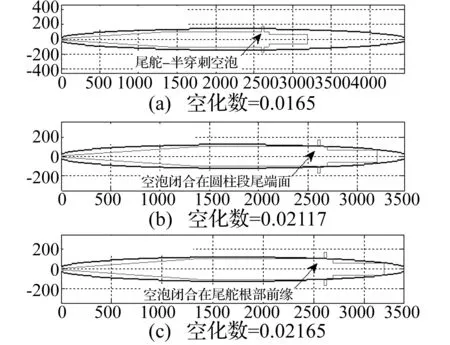
图9 三种初始直航对称空泡流型

4.3 空泡、航行体外形匹配对航行体机动能力判定

空泡外形对超空泡航行体机动运动能力影响实质为：由机动运动所需法向过载推算出航行体与超空泡间作用力，由作用力推算出航行体与空泡相对位置关系，由位置关系推算出航行体机动运动空泡最大变形量，以空泡最大变形量为约束条件衡量航行体机动运动能力。故以机动运动回转角速度为判定机动运动能力大小判据，通过仿真计算获得三种初始空泡流型下超空泡航行体机动能力的临界角速度值。

(1) 尾舵半穿刺空泡流型下临界回转角速度。以航行体直航尾舵半穿刺空泡流型为初始状态，在不同回转角速度下对航行体空泡外形进行仿真计算见图10，以许可的三种空泡流型为判据，获得对应的三个临界回转角速度：① 空泡闭合在圆柱段尾端面对称空泡流型：ωj1=1.23 rad/s；② 空泡闭合在尾舵根部前缘的非对称空泡流型：ωj2=1.38 rad/s；③ 空泡闭合在距圆柱段尾端面三分之一圆柱段长度处的非对称空泡流型：ωj3=2.01 rad/s。

(2) 尾部闭合空泡流型下临界回转角速度。以航行体直航运动空泡闭合在尾部闭合的空泡流型为初始状态，在不同回转角速度下对航行体空泡外形进行仿真计算见图11，以许可的两种空泡流型为判据，获得对应的两临界回转角速度及最小回转半径：① 空泡闭合在尾舵根部前缘的非对称空泡流型ωj1=0.38 rad/s；② 空泡闭合在距圆柱段尾端面三分之一圆柱段长度处的非对称空泡流型ωj2=1.14 rad/s。

(3) 尾舵根部前缘空泡流型下临界回转角速度。以航行体直航空泡闭合在尾舵根部前缘的空泡流型为初始状态，在不同回转角速度下对航行体空泡外形进行仿真计算见图12，以许可的一种空泡流型为判据，获得对应的临界回转角速度及最小回转半径：①空泡闭合在距尾部闭合三分之一圆柱段长度处的非对称空泡流型ωj1=0.81 rad/s。

图10 尾舵半穿刺空泡流型的三个临界角速度

5 结 论

(1) 本文通过研究空泡外形在超空泡航行体由直航运动到机动回转运动过程中的变化，用仿真方法描述空泡动态变化过程；考虑空泡外形在机动运动中变化影响因素，给出影响稳态机动回转运动空泡外形变化关键因素；通过计算分析获得角速度及离心力对空泡外形变化影响规律。在给定初始直航空泡流型条件下，通过给定评估航行体机动能力方法计算获得三种初始直航空泡流型下航行体临界回转角速度值。

(2) 本文仅通过理论分析及仿真计算方法对空泡外形对超空泡航行体机动运动能力影响进行的初步研究，所得结论尚需结合试验验证。

[1] Logvinovich G V. On law of an unsteady cavity expansion[J]. Applied Hydromechanics, Kiev, 2000, 2(74): 60-64.

[2] Vasin A D. The principle of independence of the cavity sections expansion (logvinovich’s principle) as the basis for investigation on cavitation flows[J]. RTO EN-010, 2001, 8(3): 1-28.

[3] Kirschner I N, Kring D C, Stokes A W, et al. Control strategies for supercavitating vehicles[J]. Journal of Vibration and Control, 2002, 8(2): 219-242.

[4] Kirschner I N, Rosenthal B J, Uhlman J S. Simplified dynamical systems analysis of supercavitating high speed bodies[C]. MCAV. 5th International Symposium on Cavitation,Osaka: CAV, 2003: 1-8.

[5] Lin Ming-dong,Xiang Min. Fast trajectory optimization for the time delay effect on supercavitating flight[J]. Brodogradnja, 2012, 63(3): 219-225.

[6] Zhang Guang, Yu Kai-ping. Numerlcal research on ventilated supercavity shape and flow structure in the turning motion[J]. Journal of Ship Mechanics, 2011, 15(12): 1355-1363.

[7] 张广，于开平，周景军. 超空泡航行体转弯运动流体动力特性的数值研究[J]. 应用力学学报，2012, 3(12)：25-31.

ZHANG Guang, YU Kai-ping, ZHOU Jing-jun. Numerical study of supercavitating vehicle turning motion of the fluid dynamic characteristics[J]. Chinese Journal of Applied Mechanics, 2012, 3(12): 25-31.

[8] 陈伟政，张宇文. 重力场对轴对称体稳定空泡形态影响的实验研究[J]. 西北工业大学学报，2004，22(3)：274-278.

CHEN Wei-zheng, ZHANG Yu-wen. Experimental study of the influence of gravity field on the shapes of axially symmetric steady cavity[J]. Journal of Northwestern Polytechnical University, 2004, 22(3): 274-278.

[9] Kirschner I N, Chamberlin R E. A Simple approach to estimating three-dimensional supercavitating flow fields [C]. Proceedings of the 7thInternational Symposium on Cavitation CAV, Ann Arbor, Michigan, USA,2009.

[10] 周景军，于开平. 空化器倾斜角对超空泡流影响的三维数值仿真研究[J]. 船舶力学,2011,15(1/2):74-80.

ZHOU Jing-jun, YU Kai-ping. Three dimensional numerical simulation on the influence of cavitator inclination angle to supercavity flow[J]. Journal of Ship Mechanics, 2011, 15(1/2): 74-80.

[11] 贾力平，王聪. 空化器参数对通气超空泡形态影响的实验研究[J]. 工程力学,2007,24(3):159-164.

JIA Li-ping, WANG Cong. Experimental investigation of cavitator parameters effecting on ventilated supercavity shape[J]. Engineering Mechanics, 2007, 24(3): 159-164.

[12] 杨武刚，张宇文. 攻角空化器的超空泡形态非对称特性研究[J]. 船舶工程,2007,29(6):80-83.

YANG Wu-gang, ZHANG Yu-wen. Study on the supercavity morphology asymmetric characteristic of cavitator with angle of attack[J]. Ship Engineering, 2007,29(6): 80-83.

[13] 张宇文. 空化理论与应用[M]. 陕西：西北工业大学出版社，2007.