计及静水压力影响的加筋圆柱壳塑性损伤程度预报

杨 棣，汪 玉，姚熊亮，王 军

(1.哈尔滨工程大学 船舶工程学院，哈尔滨 150001； 2. 海军装备研究院,北京 100161)

针对加筋圆柱壳动塑性损伤问题，Hoo等[1]对基础弦线模型改进后能简单、快速给出刚塑性瞬态变形；Lellep等[2]假设圆柱壳为一端固支一端简支梁，其计算结果适用于较大范围的材料参数;Cichocki等[3]用非线性有限元程序ABAQUS/ Explicit计算结构塑性变形；姚熊亮[4]用大型有限元计算软件ANSYS/LS-DYNA对圆筒结构进行数值实验研究，给出人工边界在确定边界约束的应用；Islam等[5]用ABAQUS软件模拟药包爆炸产生的冲击波与圆柱壳结构相互作用过程，发现材料几何非线性；马会防等[6]用该软件模拟静水压力与爆炸载荷同时作用的圆柱壳动力响应。

理论计算加筋圆柱壳塑性大变形方法较少，且研究时仅考虑冲击波载荷，未计及静水压力作用。实际潜艇因常处于不同潜深，因此在研究加筋圆柱壳的动塑性损伤时静水压力不可忽略。本文将截取的典型舱段简化为两端刚固的圆柱壳动力学模型，在保持相关动力学因子相同前提下用动力放大系数将静水压力变为矩形脉冲，使作用在动力学模型上的载荷形式更具真实性。用冲击波作为平面波的假设截取损伤最严重舱段为模型长度，采用动力学原理对其塑性损伤进行理论推导，获得计及静水压力作用下的加筋圆柱壳典型舱段典型位置塑性大变形快速算法。理论计算结果与有限元软件仿真及实验结果对比吻合良好，表明该算法能较好对潜艇典型结构处动塑性损伤程度进行预测。

1 加筋圆柱壳动力学模型建立

1.1 载荷形式

在水下爆炸载荷作用下圆柱壳动塑性损伤分析过程中，载荷形式为分析动力响应重点。本文在冲击波载荷基础上引入静水压力影响，目的为模拟潜艇潜深时遭遇武器攻击状态。研究冲击波载荷形式，通过大量水下爆炸试验及对爆炸相似律分析，认为炸药在自由场下爆炸产生的冲击波压力P1呈指数形式衰减。冲击波峰值压力Pm与冲击波指数衰减时间常数θ的经验公式[7]为

(1)

式中：W药为装药量(kg)；R为爆距(m)。

分析研究冲击载荷作用下圆柱壳动塑性损伤时需采用矩形脉冲，而冲击波为指数型脉冲，通过分析结构最终塑性变形与相关参量的关系[7]知：

(2)

式中：G为由结构动力特性决定的函数；Ii为作用于圆柱壳的等效冲量；Pi为作用于圆柱壳的等效载荷。

通过保持冲量Ii相等，在冲击波对圆柱壳结构造成的塑性损伤程度保持不变前提下，将冲击波载荷由指数型脉冲转化为矩形脉冲。

作用于圆柱壳的等效冲量为

(3)

作用于圆柱壳的等效冲击波载荷为

(4)

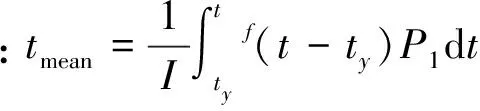
由于相同大小脉冲载荷及静载作用于同一多自由度系统产生的动力响应大小不同，可获得动力放大系数。利用此放大系数可将静载转化为动载的同时保持动力响应一个参量相同。本文通过研究动力放大系数，将静水压力转化为作用于圆柱壳的矩形脉冲动载荷。静水压力持续作用在圆柱壳上，潜艇在深水中受力相当于耐压壳体受均匀载荷，即

P2=γh深

(5)

式中：γ为水比重；h深为圆柱壳中心距水面距离。

计算动力放大时简化力学模型。由于加筋圆柱壳足够长，可视为两端刚固的梁模型模拟加筋圆柱壳的塑性动力响应过程。放大系数为

(6)

式中：w动为动载下梁中点位移，可用模态叠加法[8]由大量工况试算获得；w静为静载下梁中点位移,即

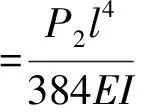
(7)

梁运动方程为

(8)

式中：EI为梁刚度；m为梁单位长度质量。

采用振形叠加法得：

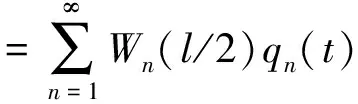
(9)

式中：Wn(l/2)为n阶固有频率对应的振形函数；qn(t)为n阶固有频率对应的时间函数。

编程求解上述方程。n取不同值时所得结果与有限元结果对比，获得n=10 000时结果满足工程精度。故本文采用模态叠加法，n取10 000。

作用于加筋圆柱壳的静载转化为脉冲载荷(作用时间tmean)为

(10)

作用于加筋圆柱壳的脉冲压力可表示(作用时间tmean)为

Pi=P1i+P2i

(11)

1.2 加筋圆柱壳动力学模型选取

基于冲击波为平面波假设，由冲击波峰传播规律，选载荷作用范围作为分析加筋圆柱壳在水下爆炸载荷作用下损伤相对严重的典型位置，见图1。用不等式条件获得分析加筋圆柱壳动力损伤效应的动力学模型选取的典型舱段模型长度为

(12)

式中：Rmin为最短爆距；a为圆柱壳半径；ln为加筋圆柱壳两横舱壁间长度；n为满足不等式舱段个数；l为圆柱壳计算模型长度。

由于加筋圆柱壳足够长，且在舱壁处为强构件，可设加筋圆柱壳塑性损伤动力学模型边界条件为两端固支，见图2。为简化计算，加筋圆柱壳材料设为理想刚塑性。因动力载荷作用时间较短，可认为壳体为小变形，壳体轴力忽略不计。

分析加筋圆柱壳塑性动力响应中引入无量纲量为

(13)

式中：tmean为脉冲载荷作用时间；μ=2h厚ρs+m0为薄壳单位中面面积上壳体质量与薄壳单位中面面积上水的附加质量之和；N0为极限膜力；M0为极限弯矩；a为圆柱壳半径；L为典型舱段半长；x为计算所需位置；h厚为将圆柱壳小筋按面积等效成圆柱壳体后圆柱壳厚的一半；σ0为屈服极限。

图1 圆柱壳典型舱段长度选取示意图

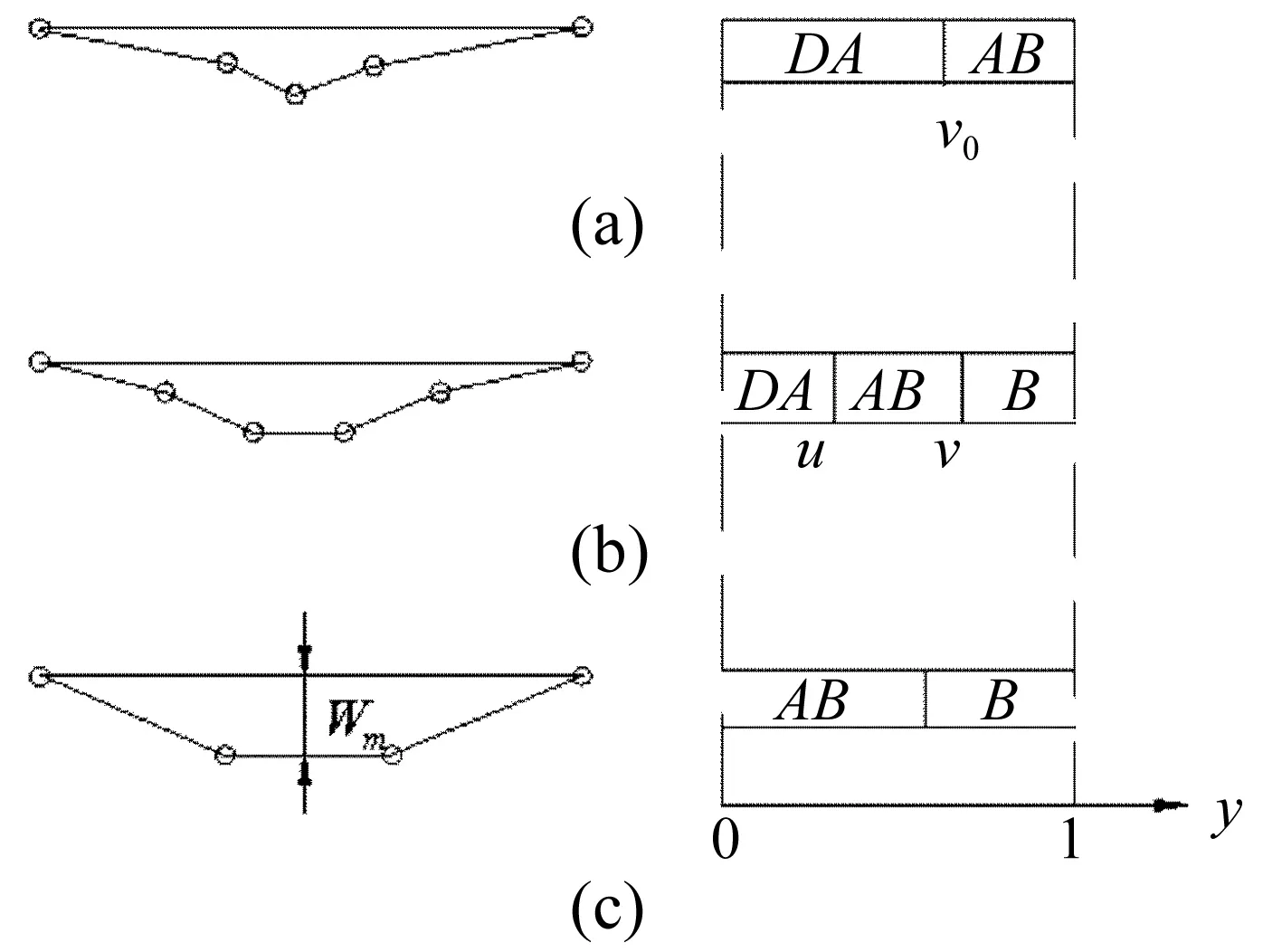
图4 圆柱壳塑性运动过程示意图

在假设冲击波为平面波前提下，加筋圆柱壳受力见图3，取单位面积圆柱壳结构进行受力分析，其运动方程为

(14)

式中：θ为冲击波入射方向与圆柱壳法线方向夹角(cosθ=b/a，b的选取见图2)；上撇为对y求导；点为对t求导。

由于材料的非线性，分析加筋圆柱壳塑性动力响应时采用简化的Tresca屈服条件[9](图3)。壳体处于运动第一阶段0≤τ≤1时存在两塑性格式不同区段(设y=v0为其分界圆)，见图4(a)。在0≤y≤v0内，n=-1,-1≤m≤1；在v0≤y≤1内，有m=1,n=-1，利用塑性铰处弯矩、速度、位移连续条件，得：

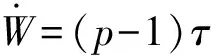
(15)

τ=1时脉冲载荷卸去，壳体进入第二阶段，此时壳体半长范围内出现三个塑性区段，见图4(b)。设壳体半长内三个区段分界为u及v。τ≥τ1时，运动进入第三阶段，壳体出现两个塑性区，见图4(c)，最大塑性变形发生在壳体中部记为Wm，据壳体处于不同时刻、不同塑性格式及在塑性铰处弯矩、速度、位移连续条件，分析加筋圆柱壳塑性动力响应过程[10]，得：

(16)

式中：τ1为第二阶段结束时间；τf为圆柱壳运动结束时间；u，z为中间变量,即

(17)

(18)

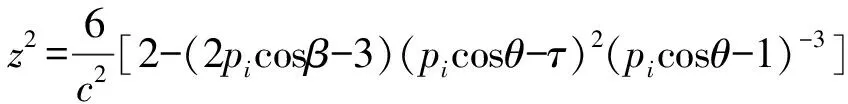
(19)

v=1时第二阶段运动结束，对应时刻为τ1。将u=u1，z1=1-u1，代入式(19)，可求出τ1为

τf=τ1+

(20)

利用式(13)可求得圆柱壳典型舱段中部挠度最大值为

(21)

2 动力学模型有效性验证

用有限元软件建立长74.4 m加筋圆柱壳模型，见图5。爆点位置正对典型舱段中部，测点为爆点对应圆柱壳最近点，A为爆点，B为测点。利用式(12)求出典型局部舱段长为28.8 m，即将三个舱段长度为研究对象，与有限元软件计算结果对比，截取长度相当,见图6。

为比较不同水深对结构动塑性损伤影响，将图5中加筋圆柱壳结构数据及工况代入式(21)编程计算，所得理论计算结果与仿真结果对比，见表1。

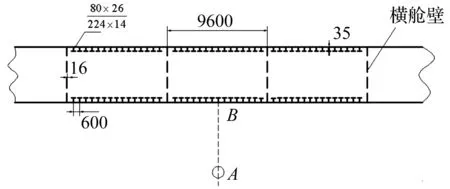
图5 圆柱壳尺寸及爆点位置示意图

图6 数值仿真截取的典型舱段

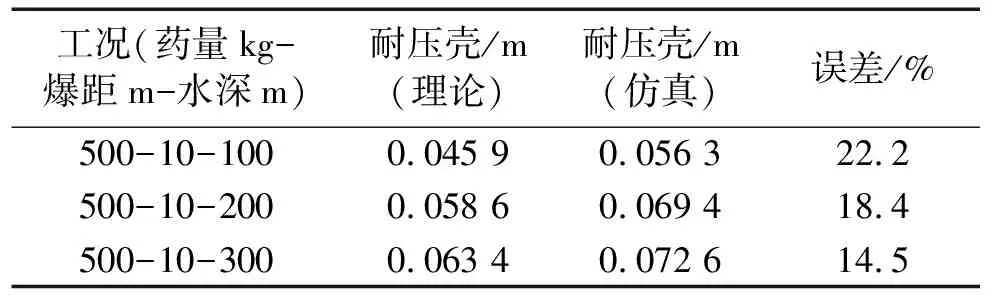
表1 加筋圆柱壳中点挠度理论值与仿真值对比结果

与此同时，用试验[11]对理论予以验证。圆柱壳试验模型长1.2 m，直径0.275 m，壳厚2 mm，试验中将圆柱壳模型两端焊接固定于装置两端。由于作用在模型上的水下爆炸载荷含冲击波载荷及气泡载荷，试验分两段测得圆柱壳中点挠度值，本文选冲击波阶段测量值对比验证，其计算值用式(15)积分后代入式(21)获得，即

(22)

将装药等工况及圆柱壳结构尺寸代入式(22)计算所得对比结果见表2。

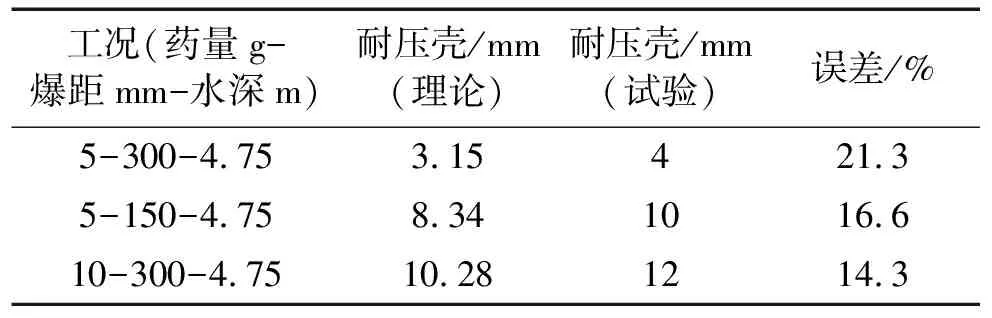
表2 圆柱壳中点处挠度理论值与试验值对比结果

由表1、2知，随静水压力的增大药量增大爆距较小、塑性变形增大。误差产生原因为①本构关系不同。本文动力学模型采用理想刚塑性材料，而实际加筋圆柱壳材料为弹塑性材料；②载荷形式不同。本文设作用在动力学模型上的为矩形脉冲载荷，而实际为指数型脉冲载荷；③网格大小不同。网格的大小可导致有限元软件计算精度不同。虽理论计算与有限元软件仿真及试验结果有一定误差，但仍在工程精度许可范围内，故该动力学模型能较好模拟计及静水压力作用下加筋圆柱壳的动塑性损伤过程，工程预报时可借鉴。

3 结 论

本文基于潜艇主要结构是加筋圆柱壳的实际情况，截取典型舱段简化成两端刚固的圆柱壳动力学模型。利用动力学相关原理获得计及静水压力影响的加筋圆柱壳受冲击波载荷作用下典型位置挠度变形计算方法，通过自主编程所得计算结果与有限元仿真及试验结果对比分析，结论如下：

(1)保持动力响应的一个参数相同，将静水压力转化为动载，利用冲量相等原理将冲击波转化为矩形脉冲载荷共同作用于加筋圆柱壳动力学模型的方法可行。

(2)将冲击波设为平面波，获得水下爆炸冲击波作用下局部典型舱段选取方法，所选舱段长度与有限元仿真圆柱壳模型塑性损伤程度相似区域基本一致，证明此截取方法具有工程实用性。

(3)基于平面波假设，将冲击波压力乘以一个入射角度作为作用于圆柱壳上的径向力，利用动力学原理对简化的两端刚固圆柱壳模型进行动力分析，获得典型舱段典型位置挠度变形计算方法。将计算结果与有限元仿真及试验结果对比，误差在工程许可范围内，表明该动力学模型能较好预测计及静水压力影响的加筋圆柱壳动塑性损伤程度。

[1] 北京工业学院八系编写组.爆炸及其作用(上册)[M].北京:国防工业出版社,1979.

[2] Lellep J,Torn K.Plastic response of a circular cylindrical shell to dynamic loadings[J]. International Journal of Impact Engineering, 2004, 30(5):555-576.

[3] Kwon Y W,Cunningham R E. Comparison of USA-DYNA finite element models for a stiffened shell subject to underwater shock[J]. Computers & Structures, 1998, 66(1): 127-144.

[4] 姚熊亮.圆筒结构水下爆炸数值实验研究[J].哈尔滨工程大学学报,2002,23(1):5-9.

YAO Xiong-liang.Numerical experiment research of cylinder in underwater explosion[J]. Journal of Harbin Engineering University, 2002, 23 (1): 5-9.

[5] Islam M N, Kormi K,Al-Hassani S T S. Dynamic response of a thin-walled cylinder to side pressure pulse[J]. Engineering Structures, 1992, 14(6): 395-412.

[6] 马会防,谌勇,华宏星,等.静水压对加筋圆柱壳受水下爆炸冲击载荷作用的影响[J].噪声与振动控制,2007,6(3):16-19.

MA Hui-fang, CHEN Yong, HUA Hong-xing, et al.The influence of hydrostatic pressure to the stiffened cylindrical shell subjected to underwater explosion shock loading[J]. The Control of Noise and Vibration, 2007, 6 (3):16-19.

[7] Youngdahl C K. Influence of pulse shape on the final plastic deformation of a circular plate[J]. Int J Solid Struct, 1971(7): 1127-1136.

[8] Rao S S.机械振动[M].北京:清华大学出版社,2009.

[9] 杨桂通,熊祝华.塑性动力学[M].北京:清华大学出版社,1984.

[10] Torn L K. Plastic response of a circular cylindrical shell to dynamic loadings[J]. International Journal of Impact Engineering, 2004 (30):555-576.

[11] Brett J M, Yiannakopoulos G, van der Schaaf P J. Time-resolved measurement of the deformation of submerged cylinders subjected to loading from a nearby explosion[J]. International Journal of Impact Engineering, 2000(24): 875-890.